산악지형에 설치된 풍력발전단지에 의한 도플러 주파수 추출 및 분석

1. 서 론

현재 전 세계 각국에서는 석유자원의 오염문제 및 고갈에 대비한 신재생 에너지 개발을 위한 다양한 연구가 수행되고 있다. 이러한 신재생 에너지 생성 방법들 중 설치비용, 건설기간 및 에너지 효율에서 가장 유망한 방법 중 하나가 풍력발전이며, 이로 인하여 다양한 형태의 풍력발전 기법들이 개발되고 있다. 이러한 경향에 따라 현재 우리나라 정부도 풍량 및 풍질이 우수한 해안지대 및 산악지대에 풍력발전단지를 활발히 건설하고 있다.

하지만 풍력발전단지가 무분별하게 건설될 경우, 풍력발전단지 인근에서 운용 중인 군사 레이더에 다양한 영향들을 초래할 수 있으며, 결국 국가 안보에 큰 위협이 될 수 있다. 여러 요인들 중 특히 문제가 되는 것이 풍력발전기의 회전 시에 반사되는 레이더 신호의 도플러 변조(Doppler modulation)인데, 도플러 변조가 발생할 경우 레이더에 수신되는 신호의 위상을 파괴하여 추적 레이더 및 영상 레이더의 성능에 심각한 영향을 줄 수 있다.

풍력발전기의 도플러 주파수로 인한 문제점을 분석하여 사전에 그 해결책을 제시하기 위하여, 본 논문의 저자들은 최근 국내 최초로 해상에 설치되는 풍력발전기의 운동 모델링 및 전자파 산란기법을 적용한 시변(time-varying) 도플러 영상을 분석하였다 [1]. 하지만 해상의 경우 레이더 시선(line-of-sight) 상의 장해물이 거의 없는데 반하여, 산악지형의 경우 지형으로 인한 다양한 형태의 차폐(blockage)가 발생하기 때문에 이를 고려한 도플러 주파수 분석이 필요하다.

본 논문에서는 산악지형에 건설되는 풍력발전기의 도플러 주파수를 추출하고 분석할 수 있는 기법을 제안한다. 제안된 기법은 기존의 해상에 설치되는 풍력발전기 도플러 분석 기법[1]을 기반으로 한 기법이며, 산악지형의 삼각형 모델링, 레이더 신호의 직진성 및 산악지형의 삼각형을 고려한 차폐분석, Rodriguez 회전공식을 이용한 풍력발전기 운동 모델링 및 처프(chirp)신호를 이용한 레이더 신호 모델링으로 구성되어 있다. 물리광학(physical optics) 기법[2]을 적용하여 얻어진 블레이드의 레이더 단면적(radar cross section: RCS)을 적용한 결과, 풍력발전기의 시변 도플러 주파수를 성공적으로 추출할 수 있었으며, 산악지형에 의한 차폐 현상도 성공적으로 분석할 수 있었다.

2. 이론 및 제안된 기법

2.3 산악지형 모델링, 차폐분석(blockage analysis) 및 신호처리 절차

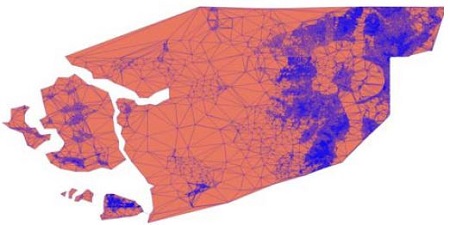
풍력발전단지가 설치되는 산악지형의 경우, 풍력발전기 블레이드와 레이더 사이의 산악지형으로 인한 차폐효과 분석을 위하여 좌표 3개를 반시계 방향 순서로 연결한 삼각형 패치(patch)로 모델링 할 수 있다(Figure 1 참조). 이는 전자파 수치해석 기법에서 널리 적용되는 모델링 방법이다. 특히 고주파 shooting and bouncing ray 기법[2]에서 직진하는 전자기파가 표적에 입사하는지 여부를 판별하는데 매우 효과적이다.

Figure 1:

Modeling of the mountain using triangles

하지만 매 샘플링 시간별로 회전하는 풍력발전기 블레이드의 각 산란원들과 레이더 사이에 수 만개의 패치의 차폐 여부를 확인할 경우, 계산 시간이 기하급수적으로 증가할 수 있다. 따라서 본 논문에서는 계산시간을 단축시키기 위하여 다음 식과 같이 레이더-블레이드 중심을 연결한 직선 및 레이더-산악 좌표를 연결한 직선들 사이의 각도를 이용하였다.

$\[ {\theta }_l=\frac{{cos}^{-1}\left(\overline{rc}\bullet \overline{rp}\right)}{\left|\overline{rc}\right|\left|\overline{rp}\right|} \]$

(9)

위 식에서 $$ \overline{\mathit{rc}}$$는 레이더와 블레이드 중심 사이를 연결한 벡터, $$ \overline{\mathit{rp}}$$는 레이더와 산악 모델링 좌표를 연결한 벡터이다. θ_l을 이용하여 빔폭 이내에 들어오는 좌표를 포함하는 패치만 차폐분석에 적용할 경우, 실시간 도플러 추출이 가능하다.

산악지형의 삼각형 패치에 의한 레이더 시선 차폐 여부는 고주파 광선추적 기법에서 널리 쓰이는 기법을 적용하여 구할 수 있다. 이 기법은 레이더 시선과 삼각형을 포함하는 평면의 교점을 구한 후, 교점이 삼각형 내부에 있는지를 검사하여 차폐 여부를 판별하는 방법이다[8].

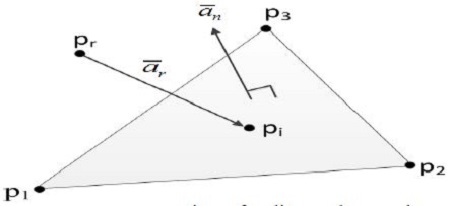
우선 직선과 평면의 교점을 구하기 위하여, Figure 2와 같은 삼각형 평면에서 법선 방정식을 다음과 같이 나타낼 수 있다.

Figure 2:

Intersection of a line and a patch

$\[ {\overline{a}}_n=\overline{p_1{p}_2}\times \overline{p_1{p}_3} \]$

(10)

위의 법선 벡터를 이용하여 Figure 2의 평면을 다음 식과 같이 표현할 수 있다.

$\[ {\overline{a}}_n\bullet \left({\overline{p}}_i-{\overline{p}}_1\right)=0 \]$

(11)

위 식에서 $$ {\overline{p}}_i$$는 평면상의 교점 p_i의 위치벡터 (p_xi,p_yi,p_zi)이고, $$ {\overline{p}}_1$$은 점 p₁의 위치벡터 (x_p1,y_p1,z_p1)이다. 레이더가 위치한 점 p_r로부터 $$ \overline{p_i}$$로의 단위벡터를 $$ {\overline{a}}_r$$이라고 가정할 경우, p_r에서 p_i까지의 벡터는 다음과 같이 표현할 수 있다.

$\[ {\overline{p}}_i={\overline{p}}_r+\alpha {\overline{a}}_r \]$

(12)

위 식에서 $$ {\overline{a}}_r$$ 방향의 가중치 α를 구하기 위하여 식 (12)을 (11)에 대입하여 정리하면 다음과 같이 표현할 수 있다.

$\[ \alpha =\frac{{\overline{a}}_n\bullet \left(\overline{p_1}-{\overline{p}}_r\right)}{{\overline{a}}_n\bullet {\overline{a}}_r} \]$

(13)

식 (12) 및 (13)을 이용하여 교점의 벡터 $$ {\overline{p}}_i$$를 찾은 후, 이 점이 패치의 외부에 존재할 경우에는 차폐하지 않으므로, 이를 판별하는 것이 중요하다. 이를 위하여 패치의 각 꼭지점의 위치벡터와 $$ {\overline{p}}_i$$를 연결한 벡터 $$ \overline{p_1{p}_i} , \overline{p_2{p}_i} , \overline{p_3{p}_i}$$를 정의 한 후, 다음과 같이 삼각형의 각 선분과의 외적을 정의할 수 있다.

$\[ \overline{A}= \overline{p_1{p}_i} \times \overline{p_1{p}_2} , \overline{B}= \overline{p_2{p}_i} \times \overline{p_2{p}_3} , \overline{C}= \overline{p_3{p}_i} \times \overline{p_3{p}_1} \]$

(14)

만약 p_i가 패치 내부에 존재할 경우, 위 세 벡터는 같은 방향을 향하게 되므로 다음과 같이 서로 간의 내적이 0 또는 양의 실수이다.

$\[ \overline{A}\bullet \overline{B}\ge 0,\overline{B}\bullet \overline{C}\ge 0,\overline{C}\bullet \overline{A}\ge 0 \]$

(15)

즉, 식 (14)를 만족하는 (11)이 레이더 시선을 차폐하는 패치가 된다.

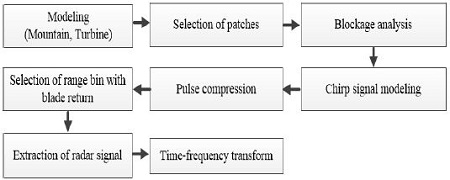
앞서 언급된 이론들을 종합한 전반적인 신호처리 절차는 Figure 3과 같다. 우선 Figure 1과 같이 풍력발전기가 설치될 산악지형 및 풍력발전기를 모델링 한 후, 계산 시간 단축을 위하여 식 (9) 및 안테나 빔폭을 이용하여 빔폭 이내에 존재하는 패치만 선택한다. 이를 이용하여 식 (10) ~ (15)와 같이 블레이드의 각 산란원의 차폐여부를 확인한 후, 식 (6)과 같이 반사되는 처프 신호를 모델링 한다. 모델링 된 신호를 참고 문헌[5][6]에 소개된 정합필터링 한 후 식 (7)의 거리측면도를 얻을 수 있으며, 최대에너지를 가지는 거리성분을 선택하여 블레이드에서 반사된 신호를 추출한 후, 최종적으로 시간-주파수 변환을 통하여 시변 도플러 주파수를 분석하게 된다.

Figure 3:

Signal processing procedure

3. 시뮬레이션 결과

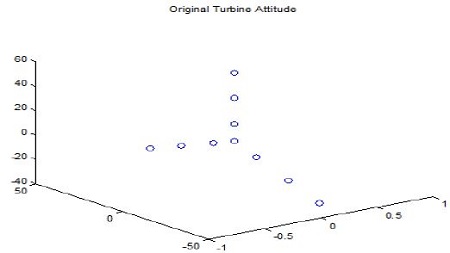
시뮬레이션 조건은 Table 1과 같이 일반적으로 사용되는 L-band 레이더를 사용하였으며, 표적을 한 거리성분에 표현하기 위하여 1.5MHz 대역폭(해상도 = 100 m)을 사용하였다. 또한 블레이드의 시변 도플러가 최악인 상태를 고려하여 발전기와 레이더 사이 각도를 90로 설정하였으며, 14.4 RPM(rotation per minute)으로 회전하는 블레이드 하나당 3개의 산란점으로 블레이드를 모델링 하였다(Figure 4). 산란점의 크기는 중심에서부터 [1 5 10 3] dB로, 블레이드를 3등분으로 나눈 후에, 각각의 평균 RCS 물리광학 기법으로 구하여 설정하였다. 안테나 빔폭은 2.2°의 pencil beam을 고려하였다. 블레이드 장동운동의 크기는 일반적으로 회전 성분에 비하여 매우 작으므로, 거의 0에 가까운 0.0001 radian으로, ω_n = 4π rad/s로 설정하였다.

Table 1:

Simulation condition

Figure 4:

Blade modeling

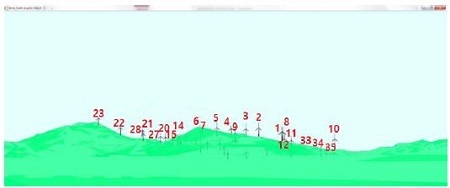
산악지형의 경우, 강원도 내에 위치한 산의 캐드 데이터를 구입하여 모델링 하였으며, 레이더 좌표 편의상 (x,y,z) = (153,650,0.02) km로 설정하였다. 또한 풍력발전기 건설 장소는 레이더에서 30mm 거리로 설정한 후, 균일한 간격으로 35대의 풍력발전기를 배치하였다. Figure 5는 레이더와 풍력발전단지 사이의 관측 상황을 나타낸다.

Figure 5:

Observation geometry

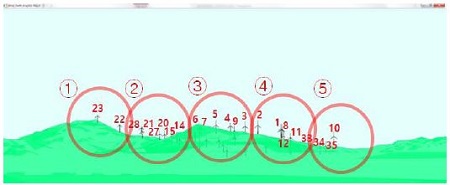
레이더에서 바라본 차폐 분석 결과는 Figure 6과 같다. 그림에서 보는 바와 같이, 총 23개의 발전기가 레이더에 의해서 발견되는 것을 알 수 있다. 레이더가 스캔할 경우, 관측각도 및 차폐 정도에 따라서 매우 변할 수 있기 때문에, Figure 7과 같이 5개의 구역으로 나누어 대표적인 풍력발전기의 미세도플러를 분석하였다.

Figure 6:

Result of blockage analysis

Figure 7:

Sectors for Doppler extraction

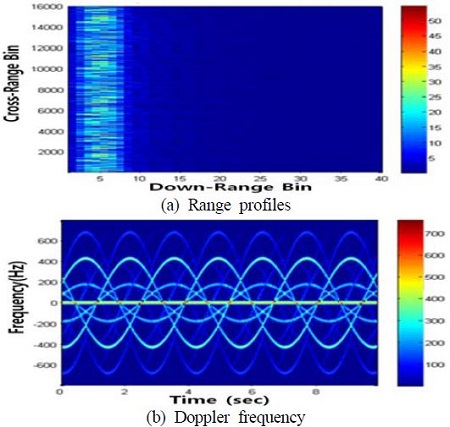
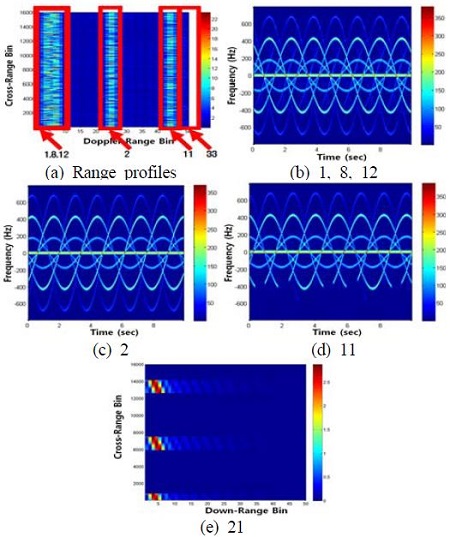
1번 영역 풍력발전기의 거리측면도 및 미세도플러 결과는 Figure 8과 같다(2.2절 참조). 그림에서 보는 바와 같이, 거리측면도의 경우 풍력발전기가 위치한 거리성분에서 레이더 신호가 시간에 따라 매우 변화하는 것을 확인할 수 있었으며, 도플러 주파수의 경우 23번 발전기가 안테나 빔에 동시에 포함되어 중첩됨을 확인할 수 있다. 또한 최대 도플러 주파수는 $$ f_d=\frac{2\upsilon }{\lambda }\mathit{cos}{\theta }_a$$ 공식(θ_α = 90°)을 적용할 경우, 681 Hz로 정확한 도플러 주파수 크기를 확인할 수 있으며, 블레이드 회전 속도 14.4 회전/분에 해당하는 각속도 1.5080 rad/s를 이용하여 계산된 시변 주파수 주기 4.1667 Hz와 거의 유사함을 확인할 수 있다. 장동운동의 경우, 크기가 회전운동보다 훨씬 작기 때문에, 도플러 주파수의 전체 분포에는 영향을 거의 주지 않음을 알 수 있다.

Figure 8:

Range profile and Doppler frequency (sector 1)

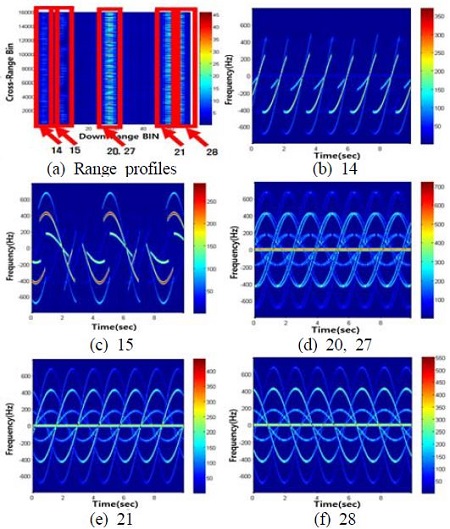
2번 영역 풍력발전기의 20호기를 관측한 결과는 Figure 9와 같다. 이 때 빔 폭 안으로 들어오는 풍력발전기는 14, 15, 20, 21, 27, 28호기이며, 이로 인하여 여러 개의 거리측면도에서 풍력발전기가 존재함을 확인할 수 있다. 14, 15호기의 경우, 지형의 차폐로 인하여 거리측면도 상에서 전체 에너지도 작음을 확인할 수 있으며, 또한 미세도플러도 주기적으로 일부 구간이 제거됨을 확인할 수 있다.

Figure 9:

Range profiles (a) and Doppler frequency results (b) ~ (f) of sector 2

그에 비하여 20호기와 27호기는 산악지형에 의하여 차폐되지 않으므로 연속적인 도플러 주파수가 형성 되었으며, 1번 영역에서와 마찬가지로 레이더 시선방향으로 동일한 거리성분에 존재하여 도플러 주파수가 중첩되어 형성됨을 알 수 있다. 또한 21, 28호기는 독립된 거리방향 성분에 존재하여 다른 터빈과 중첩되지 않음을 알 수 있다.

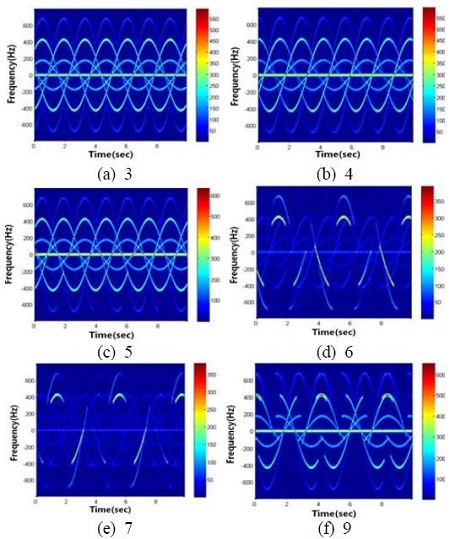
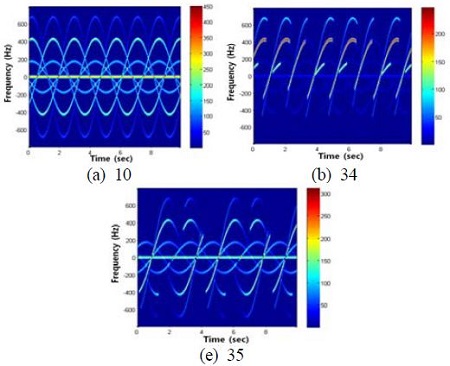
3번 영역에서는 1, 2, 8, 11, 12, 33호기가 한 레이더 빔 안에서 관측이 되었으며, 1번 및 2번 영역과 유사한 결과를 나타낸다(Figure 10). 21호기의 경우, 거의 대부분이 차폐되어 매우 일부분의 도플러 주파수가 추출됨을 알 수 있다. 4번 영역에서 관측된 3, 4, 5, 6, 7, 9호기의 도플러 주파수는 Figure 11과 같으며, 5번 영역에서 관측된 10, 34, 35호기의 결과는 Figure 12와 같다. 두 경우 모두 앞의 경우와 유사하게 전체 도플러가 형성되거나, 일부가 차폐 또는 중첩되어 형성된다.

Figure 10:

Range profiles (a) and Doppler frequency results (b) ~ (e) of sector 3

Figure 11:

Doppler frequency results of sector 4

Figure 12:

Doppler frequency results of sector 5

4. 결 론

본 논문에서는 산악지형에 설치되는 풍력발전기의 도플러 주파수를 추출하고 분석할 수 있는 기법을 제안하였다. 제안된 기법은 산악지형의 캐드 모델에서 추출된 좌표를 이용한 삼각형 모델링, 삼각형 모델링을 이용한 차폐분석, 풍력발전기 회전 모델링, 처프 신호를 이용한 레이더 신호 모델링, 시간-주파수 영상형성 기법으로 구성된다. 점산란원으로 구성된 풍력발전기를 이용한 시뮬레이션 결과, 산악지형에 의한 도플러 주파수 차폐 여부, 최대 도플러 주파수 크기 및 풍력발전기 회전으로 인한 도플러 주파수의 주기 등의 정보를 추출할 수 있었으며, 이러한 정보는 풍력발전기 근처의 레이더 운용에 있어서 매우 중요한 정보로 사용될 것이다.

References

• J. H. Jung, U. Lee, S. H. Kim, and S. H. Park, “Micro-Doppler analysis of Korean offshore wind turbine on the L-band radar”, Progress in Electromagnetics Research, 143, p87-104, (2013). [https://doi.org/10.2528/PIER13090401]
• S. H. Suk, RCS Prediction of Complex Targets, Ph. D. Dissertation, Department of Electrical Engineering, Pohang University of Science and Technology, Korea, (2001).
• J. H. Jung, K. T. Kim, S. H. Kim, and S. H. Park, “Micro-Doppler extraction and analysis of the ballistic missile using RDA based on the real flight scenario”, Progress in Electromagnetics Research M, 37, p83-93, (2014). [https://doi.org/10.2528/PIERM14040804]
• H. Gao, L. Xie, S. Wen, and Y. Kuang, “Micro-Doppler signature extraction from ballistic target with micro-motions”, IEEE Transactions on Aerospace and Electronic Systems, 46(4), p1969-1982, (2010). [https://doi.org/10.1109/TAES.2010.5595607]
• B. Mahafza, MATLAB Simulations for Radar Systems Design Using MATLAB, Champman & Hall/CRC Press LLC, (2000).
• M. Soumekh, Synthetic Aperture Radar Signal Processing with MATLAB Algorithms, John Wiley & Sons, Inc, (1999).
• S. Qian, Introduction to Time-frequency and Wavelet Transforms, Prentice Hall, (2002).
• H. K. Park, A Study on the Comparison Between EMI/EMC Analysis Methods of Vessels in the UHF Region, M.S. Thesis, Department of Electrical Engineering, Pohang University of Science and Technology, Korea, (2008).