[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 39, No. 9, pp.935-939

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Nov 2015

Received 21 Jul 2015 Revised 21 Sep 2015 Accepted 01 Oct 2015

DOI: https://doi.org/10.5916/jkosme.2015.39.9.935

직접토크제어에 의한 브러시리스 직류전동기의 센서리스 속도제어

윤경국¹ ; 오세진² ; 김덕기^†

A sensorless speed control of brushless DC motor by using direct torque control

Kyoung-Kuk Yoon¹ ; Sae-Gin Oh² ; Deok-Ki Kim^†

1 R&D Center, Seanet Co., LTD, Tel: 051-417-5802 navy2@daum.net
2 Department of Ship Operation, College of Maritime Sciences, Korea Maritime and Ocean University, Tel: 051-410-5094 osgengen@kmou.ac.kr

Correspondence to: ^†FLNG Engineering Department, Hyundai Heavy Industries, 1000, Bangeojinsunhwan-doro, Dong-gu, Ulsan 44032, Korea, E-mail: sense315@hhi.co.k, Tel: 052-203-6230

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

본 논문은 브러시리스 직류전동기의 센서리스 속도제어 방법에 관해 기술하며 센서리스 속도제어를 위해 직접토크제어 및 전류오차보상법을 사용하였다. 직접토크제어는 토크응답 속도가 빠르고 파라미터 변동에 강인하며 벡터제어 드라이브에 비해 하드웨어가 단순하고 적은 비용으로 시스템을 구성할 수 있다. 그리고 센서리스 속도제어를 위해 전류오차보상법을 사용하였는데 이 제어법은 실제 전동기 및 수식모델 전동기의 두 고정자 전류가 똑같아 지도록 제어된 전압을 전동기에 인가하여 전동기의 속도를 추정하는 방법이다. 본 논문에서 사용한 제어법은 제어기 구성이 간단하며 PI 제어기도 필요 없는 강인한 제어를 수행할 수 있다. 본 논문에서 제안하는 속도제어법의 검증을 위해 컴퓨터 모의실험을 실시하였으며 모의실험 결과 저속, 중속 및 고속영역에서의 양호한 속도특성 및 부하특성을 확인하였다.

Abstract

This paper describes sensorless speed control of brushless DC motors by using direct torque control. Direct torque control offers fast torque response, robust specification of parameter changes, and lower hardware and processing costs compared to vector-controlled drives. In this paper, the current error compensation method is applied to the sensorless speed control of a brushless DC motor. Through this control technique, the controlled stator voltage is applied to the brushless DC motor such that the error between the stator currents in the mathematical model and the actual motor can be forced to decay to zero as time proceeds, and therefore, the motor speed approaches the setting value. This paper discusses the composition of the controller, which can carry out robust speed control without any proportional-integral (PI) controllers. The simulation results show that the control system has good dynamic speed and load responses at wide ranges of speed.

Keywords:

Brushless DC motor, Direct toque control, Sensorless speed control, Current error compensation

키워드:

브러시리스 직류 전동기, 직접토크제어, 센서리스 속도제어, 전류오차보상

1. 서 론

브러시리스 직류전동기는 일반 직류전동기에 필요한 기계적인 정류장치가 없기 때문에 전기적인 스파크가 발생하지 않고 구조가 간단하며 견고한 구조를 가진다. 그리고 회전자에 발생하는 동손 등이 없기 때문에 유도전동기 등 다른 전동기에 비해 상대적으로 높은 출력을 발생시킬 수 있는 장점이 있다. 따라서 기계적인 정류에 의해 발생하는 스파크가 허용되지 않는 장소 및 효율이 높은 운전이 요구되는 장치에 브러시리스 직류전동기가 많이 사용되고 있다[1].

브러시리스 직류전동기 속도제어를 위해서는 일반적으로 홀센서 등 회전자 위치센서가 필요한데 이러한 센서를 사용하면 구동 드라이버의 비용이 증가하고 장치 크기가 커지며 노이즈 등의 영향으로 장치 신뢰성이 저하한다[2].

본 논문에서는 회전자 위치센서 등을 사용하지 않는 간단하고 강인하며 제어시스템 구현이 용이한 브러시리스 직류전동기의 새로운 센서리스 속도제어 방법을 제안한다.

본 논문의 속도추정 방법으로는 전류오차보상법을 사용하였으며 인버터 구동 방식으로 직접토크제어를 사용하였다. 전류오차보상법은 실제 전동기 및 수식모델 전동기의 두 고정자 전류가 똑같아 지도록 제어된 전압을 전동기에 인가하여 전동기의 속도를 추정하는 방법이고 직접토크제어는 토크, 자속 지령치와 전동기의 발생 토크 및 자속 값을 허용된 히스테리시스 폭 범위 안에서 서로 비교하여 최적의 공간전압 벡터를 얻기 위해 인버터 스위칭 테이블을 사용하는 방법이다[3][4].

2. 직접토크제어

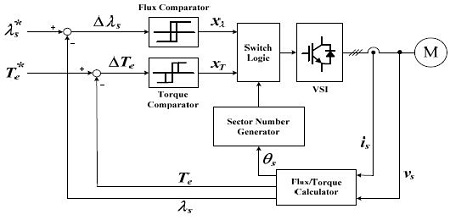
Figure 1은 직접토크제어의 블록선도를 보여준다.

Figure 1:

Scheme of direct torque control

Figure 1에서 자속 및 토크 비교기(Comparator)는 둘 다 히스테리시스 형식이며, 자속 비교기는 2가지(x_λ=+1,-1) 출력을 내보내고 토크 비교기는 3가지(x_T=+1,0,-1) 경우를 출력시킨다. 여기서 '+1'은 고정자 자속이나 토크 각의 증가를 의미하고 '-1'은 자속이나 토크 각의 감소를 나타내며 '0'은 토크 변화를 요구하지 않음을 의미한다.

Figure 1에서 λ_s^*는 자속 지령치, T_e^*는 토크 지령치이다. Δλ_s는 자속 지령치와 전동기 자속의 비교값이고 ΔT_e는 토크 지령치와 전동기 발생 토크를 상호 비교한 값이다. 그리고 θ_s는 고정자 좌표의 d축을 기준으로 표시한 고정자 자속벡터의 각이다.

Table 1은 반시계 방향으로 회전하는 고정자 기준 자속을 발생시키기 위한 스위칭 논리를 나타낸다. 입력 변수는 x_λ, x_T 및 영역(Ⅰ~Ⅵ)이며 출력 변수는 인버터 전압벡터가 된다.

Table 1:

Switching logic (counterclockwise direction)

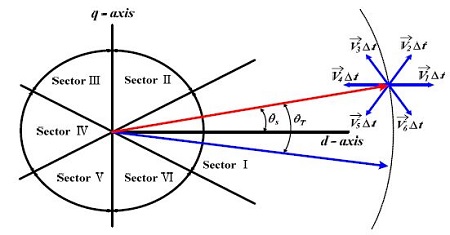
Figure 2는 직접토크제어의 개략적인 원리를 설명해준다. 각 스위칭 영역에서 자속 및 토크 조건에 따라 Table 1을 이용하여 최적의 전압벡터가 선정된다. Figure 2에서 θ_T는 고정자 및 회전자 자속벡터 사이의 토크 각이다.

Figure 2:

Principle of direct torque control

3. 센서리스 속도제어

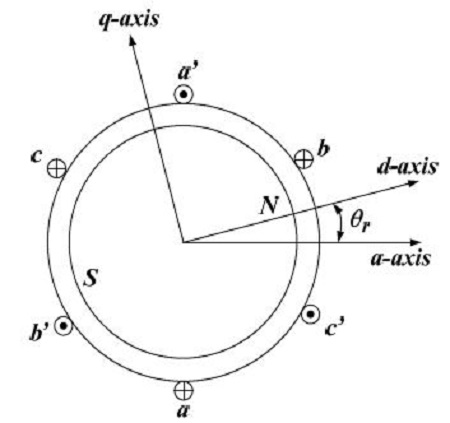
Figure 3은 2극 브러시리스 직류전동기의 모델을 나타낸다. 고정자 권선은 3상 Y결선으로 연결되어 있고 각 상은 120° 간격으로 배치되어 있으며 회전자는 영구자석이다. 일반적인 제어에서는 홀센서를 부착하여 회전자 자속 위치를 검출하여 속도제어를 수행한다.

Figure 3:

Model of BLDC Motor

직류전동기와 유사하게 브러시리스 직류전동기의 전압방정식은 다음의 식으로 표현할 수 있다.

υ = r a i a + k e ω r + L a di a dt

(1)

식 (1)에서 υ는 고정자 상전압, r_a는 고정자 저항, i_a는 상전류, k_e는 역기전력 상수, ω_r은 회전자 각속도 및 L_a는 인덕턴스이다.

식 (1)을 전류에 관한 식으로 다시 표현하면 다음과 같다.

di a dt = υ L a - r a L a i a - k e ω r L a

(2)

전력 P_e와 기계적 출력 P_m 사이의 관계는 식 (3)으로 나타낼 수 있다.

P e = E i a = P m = T e ω r

(3)

식 (3)에서 E는 역기전력이고 T_e는 토크이다. 토크 T_e는 상전류에 비례하며 식으로 나타내면 다음과 같다.

T e = k T i a

(4)

여기서 k_T는 토크 상수이다.

식 (3), 식 (4)를 이용하여 다음의 식을 구할 수 있다.

T e = E ω r i a

(5)

역기전력은 E=K_eω_r로 표현할 수 있으므로 식 (5)를 이용하여 다음의 식을 구할 수 있다.

k T = E ω r = k e ω r ω r = k e

(6)

그리고 브러시리스 직류전동기의 동적 방정식은 다음 식으로 표현할 수 있다.

T e = T L + J d ω r dt + B ω r

(7)

여기서 T_L은 부하 토크, J는 관성모멘트, B는 마찰계수이다.

식 (7)을 회전자 각속도로 표현하면 식 (8)을 얻을 수 있다.

d ω r dt = 1 J T e - T L - B ω r

(8)

식 (2), (4), (8)에 의해 브러시리스 직류전동기는 고정자 전압을 입력받아 고정자전류 및 회전자 속도를 출력하는 시스템으로 생각할 수 있다. 이것을 그림으로 나타내면 Figure 4와 같다.

Figure 4:

Input, output variables(BLDC Motor)

식 (2)를 이용하여 Figure 4의 전동기와 전기적 파라미터가 동일한 수식모델을 고려하면 Figure 5와 같이 표현할 수 있다.

Figure 5:

Input, output variables of model

Figure 5에서 수식모델의 입력 전압은 실제 전동기의 고정자 전압과 같고 입력 회전자 속도는 속도 설정값을 사용하며 고정자 전류를 출력한다. Figure 5에서 첨자 m은 수식모델 변수를 나타내고 ω_ref는 수식모델의 속도로서 속도 설정값이다.

Figure 4, 5에서 수식모델이 실제 전동기를 정확하게 표현할 경우, 실제 전동기의 전압, 전류가 수식모델과 일치할 때에는 전동기의 회전자 속도도 설정치인 수식모델의 회전자 속도와 같게 될 것이다. 식 (1)을 이용하여 과도상태를 무시한 전동기 및 수식모델의 전압방정식을 표현하면 다음과 같다.

υ = r a i a + k e ω r

(9)

식 (9)에서 전동기와 수식모델에 같은 고정자전압을 인가하면 다음과 같은 식이 얻어진다.

r a i a - i am = k e ω rm - ω r

(10)

따라서 수식모델과 전동기 고정자 전류 사이의 전류오차를 보상하면서 양자에 동일한 전압을 인가한다면 식 (10)에 의해 전동기 회전자 각속도인 ω_r이 설정치인 수식모델의 회전자 각속도 ω_rm과 같아지게 된다. 본 논문에서는 수식모델과 전동기의 전류를 일치시키는 방법으로 직접토크제어를 사용하였다.

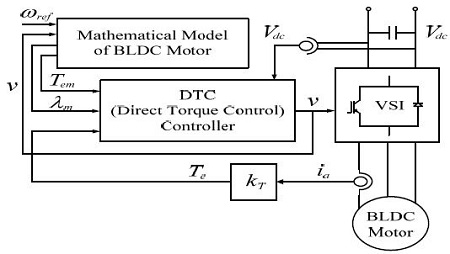
Figure 6은 본 논문에서 제안한 브러시리스 직류전동기의 센서리스 속도제어 블록선도이다.

Figure 6:

The proposed control method

Figure 6에서 λ_m은 수식모델의 자속이고 V_dc는 인버터 직류 링크 전압이다. 전동기에 인가되는 전류를 측정하여 전동기 발생토크를 계산하고 전동기에 인가되는 전압을 수식모델에 똑같이 인가하여 수식모델의 발생토크 및 자속을 계산한다. 그리고 직접토크제어 방식에 의해 인버터 전압이 발생하도록 구성되어 있다.

본 논문에서 제안한 속도제어 방식은 구현이 쉬우며 PI제어기를 사용하지 않고 센서리스 속도제어를 수행하는 아주 독특한 구조를 가진다.

4. 컴퓨터 모의실험

본 논문의 제어방식 유효성 입증을 위해 수치해석 소프트웨어인 MATLAB을 사용하여 컴퓨터 모의실험을 수행하였다. 모의실험에 사용된 브러시리스 직류전동기의 파라미터는 Table 2와 같다.

Table 2:

Parameters of motor

모의실험에서는 우선 저속, 중속 및 고속영역의 계단상 속도지령에 추종하는 속도 응답특성 및 반전속도 응답특성을 확인하려고 한다. 그리고 저속, 중속 및 고속영역에서의 부하특성도 고찰하려고 한다.

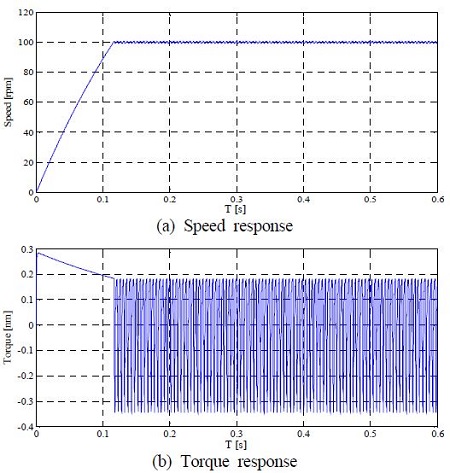
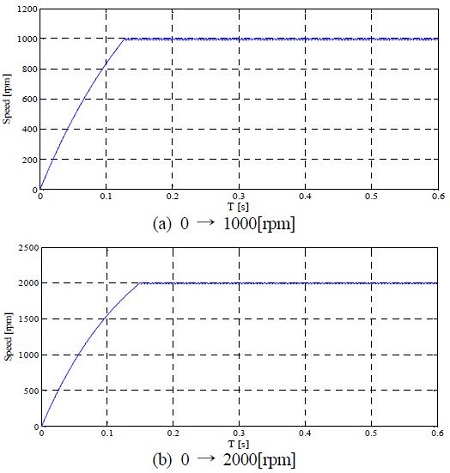
Figure 7은 100 [rpm]으로 속도지령을 인가하였을 경우의 속도 및 토크 응답을 나타내며 Figure 8은 1000 [rpm] 및 2000 [rpm]으로 각각 계단입력 속도지령을 가했을 경우의 전동기 속도 응답특성을 나타낸다. 저속영역 및 고속영역에서 센서리스 속도 응답특성이 양호함을 알 수 있다.

Figure 7:

Speed step change(0 → 100[rpm])

Figure 8:

Speed step change

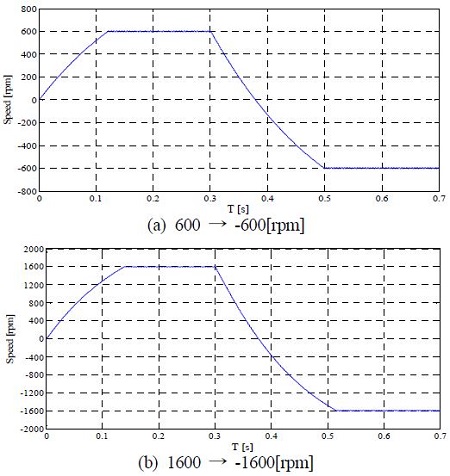
Figure 9는 600 [rpm] 및 1600 [rpm]의 속도 지령을 인가한 뒤 0.3초 후에 반전속도지령을 인가했을 경우의 속도 응답특성을 나타낸다. 그림에서 알 수 있듯이 중속 및 고속영역에서 반전속도 특성이 우수함을 알 수 있다.

Figure 9:

Speed change

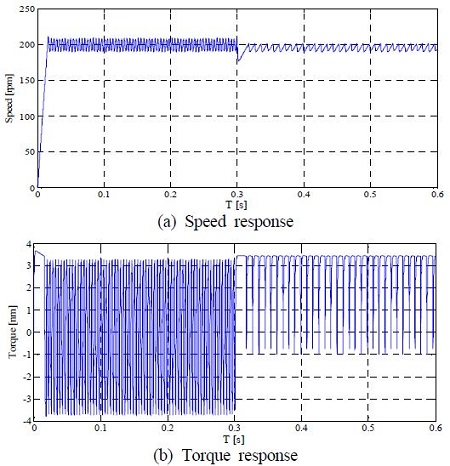
Figure 10은 200 [rpm]으로 계단 속도지령을 인가한 뒤 0.3초 후 3 [N·m]의 부하토크를 인가하였을 경우의 속도 및 토크응답을 나타낸다. 저속영역에서 부하특성이 양호함을 알 수 있다.

Figure 10:

Change of load torque(0 → 3[N·m])

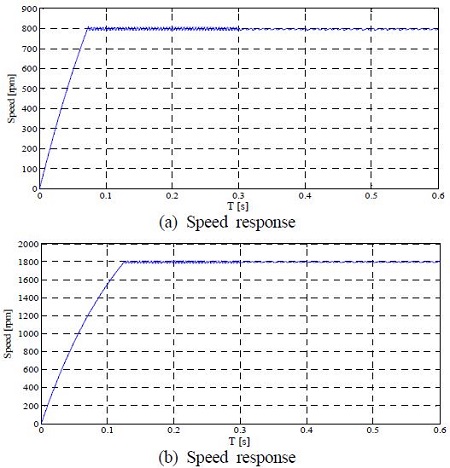
Figure 11은 800[rpm] 및 1800[rpm]으로 계단 속도지령을 인가하고 0.3초 후 3 [N·m]의 부하토크를 인가하였을 경우의 속도응답을 나타낸다.

Figure 11:

Change of load torque(0 → 3[N·m])

5. 결 론

본 연구에서는 브러시리스 직류전동기의 센서리스 속도제어를 위해 수식모델의 전류와 전동기 전류 사이의 오차를 보상하는 전류오차보상법을 사용하였으며 전동기 구동을 위해 직접토크제어를 이용하였다.

제어시스템에서 센서를 사용하지 않기 때문에 보다 신뢰성 높은 제어시스템을 구성할 수 있고 직접토크제어를 사용함으로써 파라미터 변화에 강인하며 복잡한 연산 없이 단순하게 제어시스템을 설계할 수 있다.

제어시스템의 유효성 확인을 위해 컴퓨터 모의실험을 수행하였으며 저속, 중속 및 고속영역의 속도지령에 대한 양호한 응답특성 및 부하특성을 확인하였다. 그리고 차후 실제 실험을 통하여 본 논문에서 제안한 방식의 우수성을 검증하려고 한다.

References

N. Matsui, “Sensorless PM brushless DC motor drives”, IEEE Transactions on Industrial Electronics, 43(2), p300-308, (1996). [https://doi.org/10.1109/41.491354]
K. Xin, Q. Zhan, and J. Luo, “A new simple sensorless control method for switched reluctance motor drives”, KIEE Journal of Electrical Engineering & Technology, 1(1), p52-57, (2006). [https://doi.org/10.5370/JEET.2006.1.1.052]
S. G. Oh, J. S. Kim, and S. H. Kim, “Sensorless speed control of induction motor using current compensation”, Journal of the Korean Society of Marine Engineering, 27(4), p503-510, (2003).
T. G. Habetler, F. Profumo, M. Pastorelli, and L. M. Tolbert, “Direct torque control of induction machines using space vector modulation”, IEEE Transactions Industrial Application, 28(5), p1045-1053, (1992). [https://doi.org/10.1109/28.158828]
X. Shen, Z. Q. Zhu, and D. Howe, “Sensorless flux-weakening control of permanent-magnet brushless machines using third harmonic back EMF”, IEEE Transactions on Industry Applications, 40(6), p1629-1636, (2004). [https://doi.org/10.1109/TIA.2004.836157]
G. J. Su, and J. W. Mckeever, “Low cost sensorless control of brushless DC motors with improved speed range”, IEEE Transactions on Power Electronics, 19, p296-302, (2004). [https://doi.org/10.1109/TPEL.2003.823174]
Q. Jiang, C. Bi, and R. Huang, “A new phasedelay- free method to detect back EMF zerocrossing points for sensorless control of spindle motors”, IEEE Trans. Magnetics, 41(7), p2287-2294, (2005). [https://doi.org/10.1109/TMAG.2005.851841]
T. G. Park, J. S. Ryu, and K. S. Lee, “Actuator fault estimation with disturbance decoupling”, Proceedings of the Institute of Electrical and Electronics Engineers, 147(5), p501-508, (2000). [https://doi.org/10.1049/ip-cta:20000639]
T. G. Park, and K. S. Lee, “Process fault isolation for linear systems with unknown inputs”, Proceedings of the Institute of Electrical and Electronics Engineers, 151(6), p720-726, (2004). [https://doi.org/10.1049/ip-cta:20040796]
B. Marx, D. Koenig, and J. Ragot, “Design of observers for Takagi-Sugeno descriptor systems with unknown inputs and application to fault diagnosis”, Proceedings of the Inst. Elect. Tech, 1(5), p1487-1495, (2007). [https://doi.org/10.1049/iet-cta:20060412]
S. H. Huh, S. J. Seo, I. Choy, and G. T. Park, “Design of a robust stable flux observer for induction motors”, KIEE Journal of Electrical Engineering & Technology, 2(2), p280-285, (2007). [https://doi.org/10.5370/JEET.2007.2.2.280]
T. H. Kim, and M. Ehasani, “Sensorless control of the BLDC motors from near-zero to high speeds”, IEEE Transactions on Power Electronics, 19(6), p1635-1645, (2004). [https://doi.org/10.1109/TPEL.2004.836625]

Figure 1:

Scheme of direct torque control

Figure 2:

Principle of direct torque control

Figure 4:

Input, output variables(BLDC Motor)

Figure 5:

Input, output variables of model

Figure 6:

The proposed control method

Figure 7:

Speed step change(0 → 100[rpm])

Figure 10:

Change of load torque(0 → 3[N·m])

Figure 11:

Change of load torque(0 → 3[N·m])

Table 1:

Switching logic (counterclockwise direction)

Comparator Output		Sector
x_λ	x_T	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ
+1	+1	$V 2 ⃗$	$V 3 ⃗$	$V 4 ⃗$	$V 5 ⃗$	$V 6 ⃗$	$V 1 ⃗$
+1	0	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$
+1	-1	$V 6 ⃗$	$V 1 ⃗$	$V 2 ⃗$	$V 3 ⃗$	$V 4 ⃗$	$V 5 ⃗$
-1	+1	$V 3 ⃗$	$V 4 ⃗$	$V 5 ⃗$	$V 6 ⃗$	$V 1 ⃗$	$V 2 ⃗$
-1	0	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$	$V 0 ⃗$
-1	-1	$V 5 ⃗$	$V 6 ⃗$	$V 1 ⃗$	$V 2 ⃗$	$V 3 ⃗$	$V 4 ⃗$

Table 2:

Parameters of motor

Name	Value
Rated Power	2000[W]
Rated Current	2.1 [A]
Rated Voltage	300[V
Rated Speed	2000[rpm]
Stator Resistance	5.8[Ω]
Stator Inductance	0.03[H]
Rotor Flux Linkage	0.49[Wb]
Back-EMF constant	0.28(V/rad/s)
Rated Torque	5.2[N·m]
Moment of Inertia(J)	0.00085[kg·m²]