[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 39, No. 9, pp.923-928

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Nov 2015

Received 14 Sep 2015 Revised 26 Oct 2015 Accepted 10 Nov 2015

DOI: https://doi.org/10.5916/jkosme.2015.39.9.923

FDS의 격자 종횡비에 관한 연구

김원욱¹ ; 박외철^†

A study on grid aspect ratio of fire dynamics simulator

Won Ouk Kim¹ ; Woe-Chul Park^†

1 Korea Institute of Maritime and Fisheries Technology, Tel: 051-620-5816 kwo0228@naver.com

Correspondence to: ^†Department of Fire Protection Engineering, Pukyong National University, 45 Yongso-ro, Nam-gu, Busan 48513, Korea, E-mail: wcparkk@pknu.ac.kr, Tel: 051-629-6467

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

FDS는 화재분석에 가장 많이 사용되는 프로그램 중 하나로 정확한 분석을 위하여 적정격자 선정이 필요하다. 이 연구에서는 적정격자 선정을 위하여 다양한 격자 종횡비(AR)를 선정하여 FDS v 6.1.2로 분석하였다. 계산시간은 온도 등의 변화로부터 시간평균값을 구하는데 충분히 긴 10분으로 설정하였다. 그리고 온도와 가시거리, 질량수지의 시간평균값은 준정상상태를 유지하는 200~600초 구간의 값으로부터 구하였다. 그 결과 10×10×3 [m³]와 20×20×3 [m³]의 두 공간에 각각 1 [MW]와 2 [MW]의 폴리우레탄 화재가 발생했을 때 종횡비 1~6에 대한 열방출률과 온도, 가시거리, 질량수지를 비교하였다. 열방출률은 종횡비와 공간의 크기 및 화재규모에 무관하게 정확함을 확인하였다. 또 AR≤5에서는 준정상상태의 온도와 가시거리가 잘 예측되었다. 그러나 종횡비의 증가에 따라 온도의 감소폭이 증가하였고, 질량보존의 만족도가 떨어졌다. 따라서 화재 초기의 온도와 가시거리가 중요한 요소인 성능위주설계에서 AR≥3인 경우에는 격자크기에 대한 세심한 검토가 필요함을 확인하였다. 높은 정확도가 요구되는 구획화재 시뮬레이션에는 수직방향 격자크기 0.1~0.2 [m] 이하와 종횡비 2 이하의 격자크기가 바람직함을 알 수 있었다.

Abstract

The FDS is one of the most used programs for fire analysis and needs an optimal grid selection for an accurate analysis. This study selected various grid aspect ratios (ARs) for selection of optimal grid and analyzed them with FDS v 6.1.2. A calculation time of 10 min. was used, which is enough to obtain the time average value of temperature changes. Temperature, visibility, and the time average value of mass balance are obtained from 200-600 s, which is a period of maintaining quasi-steady state. Two polyurethane fires of 1 [MW] and 2 [MW] in two enclosures of 10×10×3 [m³] and 20×20×3 [m³] were considered. Time variations of heat release rates, temperature, visibility, and mass balance were compared for ARs from 1-6. The heat release rates were accurate for all aspect ratios regardless of fire and enclosure sizes. The quasi-steady state temperature and visibility were well predicted for AR≤5. Temperature drop and skewness of mass conservation, however, increased with increasing aspect ratio. Therefore, careful investigation of the grid size is recommended in performance- based design when AR≥3, where temperature and visibility in early stage of a fire are important parameters. For accurate simulations of enclosure fires, grid sizes of 0.1~0.2 [m] and smaller in the vertical direction and AR≤2 are recommended.

Keywords:

Fire simulation, Grid size, Aspect ratio, Temperature, Visibility, Mass balance

키워드:

화재시뮬레이션, 격자크기, 종횡비, 온도, 가시거리

1. 서 론

전산유체역학에서 격자크기가 작을수록 이론적으로는 정확도가 향상된다. 그러나 격자크기를 줄이면 격자수가 늘어나고 따라서 연산횟수가 늘어나 수치적 오차도 증가한다. 또 격자수가 증가하면 계산시간과 컴퓨터의 소요 기억용량도 늘어난다. 이런 문제점으로 인해 정확도를 유지하면서 적정 격자크기를 선정하는 것이 관심의 대상이 되어왔다. 특히, 구획화재의 화재시뮬레이션에서 수직방향 격자크기 Δz는 크게 설정할 수 없다. 수직방향의 온도변화가 크기 때문에 공간 내 온도분포를 정확하게 구하기 위해서는 작은 값의 Δz를 쓸 수밖에 없기 때문이다. 따라서 Δz의 값은 작게 하되, 정확도가 크게 훼손되지 않는 범위 내에서 수직방향보다 온도변화가 작은 수평방향, 즉 x, y방향의 격자크기 Δx와 Δy는 Δz보다 큰 값을 선택하는 것이 바람직하다. 따라서 격자크기의 종횡비(aspect ratio, 이하 AR) Δx/Δz 또는Δy/Δz에 대한 조사가 필요하다. 이러한 이유로 선행연구[1][2]가 수행되었다. 국내외의 화재시뮬레이션에 대부분 Fire Dynamics Simulator(이하 FDS)[3]가 사용되고 있다. 그 예로, 최근 국내에서 수행한 선박화재 연구[4]-[6]를 들 수 있다. 특히, 선박 화재 분석을 통한 선원들의 인명 생존율 향상에 유용하게 사용될 수 있을 것이다. 이전연구[7]에서 z방향의 격자크기가 0.2 [m]일 때 x, y방향 적정 격자크기는 각각 0.5 [m] (AR=2.5) 이내로 제시되었고, 종횡비에 관한 추가연구의 필요성이 제기되었다. 본 연구의 목적은 FDS를 사용하는 화재시뮬레이션에서 격자크기 선정에 편의를 제공하는 것이다. 이를 위해 크기가 다른 2개의 공간 내 두 가지 값의 화재규모, 즉 4가지의 화재를 대상으로 다양한 종횡비를 적용하여 화재시뮬레이션을 수행하고, 종횡비가 증가함에 따른 문제점을 조사하였다.

2. 연구방법

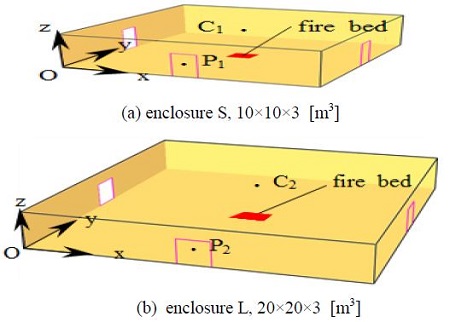
화재시뮬레이션 대상공간으로 Figure 1에 나타나 있는 바와 같이 바닥면적 10×10 [m²], 높이 3 [m]의 공간 S와 바닥면적 20×20 [m²], 높이 3 [m]의 공간 L의 두 가지를 선정하였다. 두 공간 모두 좌우 그리고 앞면의 중앙에 3개의 개방된 문을 두어 환기부족으로 인한 문제가 발생하지 않도록 하였다. 작은 공간의 문의 크기는 각각 1×2 [m²]이고, 큰 공간의 문은 각각 2×2 [m²]이다. 두 공간 모두 화원의 위치를 바닥의 중앙으로 하고, 화원의 크기를 1×1 [m²]로 가정하였다. 원점 O의 좌표를 (0,0,0), 반대편 모서리의 좌표를 작은 공간은 (10,10,3), 큰 공간은 (20,20,3)이 되도록 하였다. 여기서 좌표의 단위는 [m]이다. 연기에 의한 가시거리 감소가 인명안전의 중요 요소이므로 그을음 발생율이 가연성물질 질량의 10 [%]인 폴리우레탄이 연소하는 것으로 설정하였다.

Figure 1:

Computational domains and coordinates of two enclosures

격자 종횡비에 따른 결과의 비교지표로 열방출률과 온도, 가시거리, 물질수지를 선택하였다. 화원중심 위쪽 바닥에서부터 2.9 [m] 높이의 한 점 C₁과 C₂에서의 온도변화를 출력하였다. 성능위주설계[8]에서는 화원 위쪽 천장의 온도보다 피난구의 호흡선 높이에서 온도와 가시거리가 중요하다. 유효피난시간을 결정하는 데에 호흡선 높이에서의 온도와 가시거리가 기준이 되기 때문이다. 이에 따라 앞쪽문의 수직중심선상의 바닥에서부터 1.8 [m] 높이 점 P₁과 P₂에서의 온도 및 가시거리를 출력하였다. 한편, 질량보존의 법칙을 만족하기 위해서는 3개의 문에서의 질량유량의 합은 연료소모율이 같아야 한다. 연료소모율은 화재규모가 1 [MW]일 때 0.0526 [kg/s], 2 [MW]일 때 0.105 [kg/s]로 매우 작으므로 이를 무시하면, 3개의 문을 통한 질량유량의 합, 즉 질량수지(mass balance)는 식 (1)과 같이 0이 되어야 한다.

∫ A p u d A ≒ 0

(1)

여기서, ρ는 밀도, u는 개구부에 대한 수직방향 속도, A는 개구부의 면적이다. 외기 및 초기 온도 등 경계조건과 초기조건은 FDS의 기본값을 그대로 사용하였다. 관계식과 수치법, 경계조건 등에 관한 자세한 내용은 FDS 설명서[3][9]에 나와 있으므로 여기에서는 제시하지 않았다. 본 연구에서 조사한 종횡비와 격자크기, 열방출률은 Table 1과 같다. 크기 10×10×3 [m³]의 공간 S에서는 z방향 격자크기(Δz)를 0.1 [m]로 고정하고 x, y방향 격자크기는 0.1~0.6 [m], 즉 Δx = Δy = 0.1~0.6 [m]로 잡았다. 이것은 종횡비(AR) Δx/Δz = 1~6에 해당한다. 20 × 20 × 3 [m³] 의 공간 L에서는 Δz를 0.2 [m]로 하고 Δx = Δy = 0.4~1.2 [m](AR = 2~6)에 대한 화재시뮬레이션을 수행하였다. 본 연구에서 Δz를 0.1 [m]와 0.2 [m]로 한정한 것은, 구획화재에서 Δz≥0.3 [m]로 설정하는 것은 서론에서 언급한 바와 같이 정확한 온도분포를 계산하는데 너무 크기 때문이다.

Table 1:

Grid sizes and heat release rates investigated

위의 두 공간 S 및 L에서 각각 두 가지의 화재규모 1 [MW]와 2 [MW], 총 4가지의 공간크기-화재규모의 조합에 대해 화재시뮬레이션을 수행함으로써 연구결과의 신뢰성을 높이도록 하였다. 결과와 비교할 실험 데이터가 없으므로, 이 4가지 조합별로 격자 종횡비에 따라 결과를 서로 비교하였다. Table 1에 표시한 11가지의 격자크기로 각각 화재규모 1 [MW]와 2 [MW], 즉 총 22가지의 경우에 대한 화재시뮬레이션을 수행하였으며, 모두 균일격자를 사용하였다. 인위적인 화재성장곡선을 적용하지 않음으로써 발화 후 바로 열 방출률이 일정하게 유지되도록 하였다.

본 연구에 FDS v6.1.2를 사용하였고, 계산시간은 온도 등의 변화로부터 시간평균값을 구하는데 충분히 긴 10분으로 설정하였다. 온도와 가시거리, 질량수지의 시간평균값은 준정상상태를 유지하는 200~600초 구간의 값으로부터 구하였다.

3. 결과 및 토의

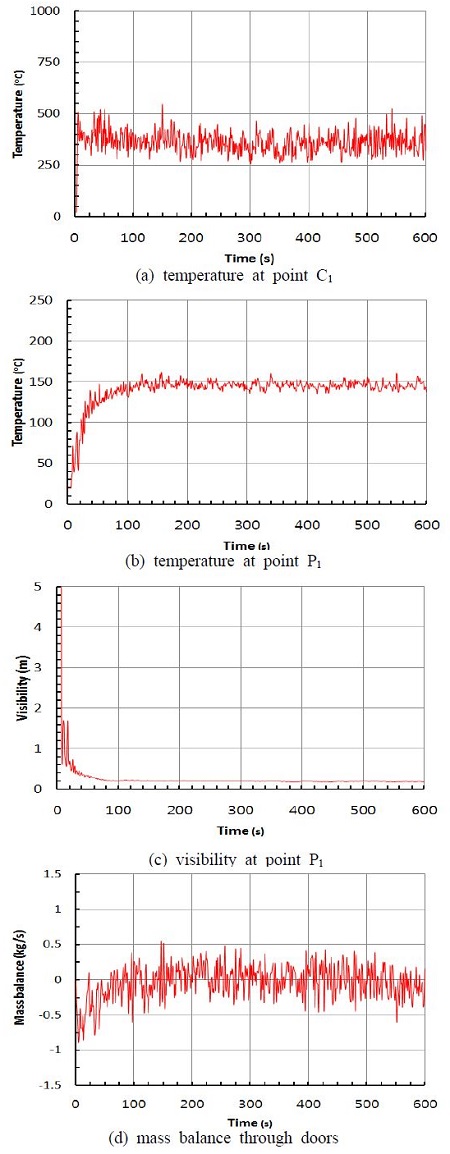
AR=2~6의 결과를 모두 하나의 흑백그림에 표시하면 식별하기가 곤란하므로 본 논문에서는 AR= 2, 4, 6의 세 결과만 제시하였다. 먼저 참고용으로 작은 공간(10 × 10 × 3 [m³])의 AR=1, 즉 격자크기 Δx = Δy = Δz = 0.1 [m], 화재규모 1 [MW]에 대한 화재시뮬레이션을 수행하였다. i5-3347U dual core PC에서 40시간이 소요되었다. Figure 2는 작은 공간, AR=1, 1 [MW]의 화재시뮬레이션 결과를 나타낸 그림이다. 온도와 가시거리 및 질량수지의 변화가 모두 준정상상태에 도달해 200~600초 사이의 값으로부터 시간평균값을 구하였다. 화원 바로 위 천정부근에 위치한 점 C₁에서의 평균온도는 355 [^oC]였다. 앞문 수직중심선상의 바닥에서부터 1.8 [m] 높이에 위치한 점 P₁에서의 평균온도는 146 [oC], 평균가시거리는 0.2 [m]였다. 한편, 3개의 문에서의 평균질량수지는 0.004 [kg/s]로 아주 작으므로 질량보존의 법칙을 만족하였다.

Figure 2:

Results for the enclosure S with Δx = Δy = Δz = 0.1 [m] and 1 [MW]

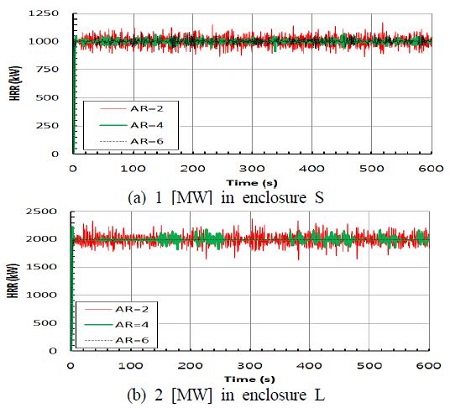
작은 공간과 큰 공간에서 각각 화재규모 1 [MW]와 2 [MW]로 입력한 후 격자 종횡비에 따른 열방출률을 Figure 3에 비교하였다. 공간과 두 가지 화재규모에서 모두 종횡비에 무관하게 입력값과 같은 1 [MW]와 2 [MW]이 출력되었다.

Figure 3:

Comparison of heat release rate for grid aspect ratios

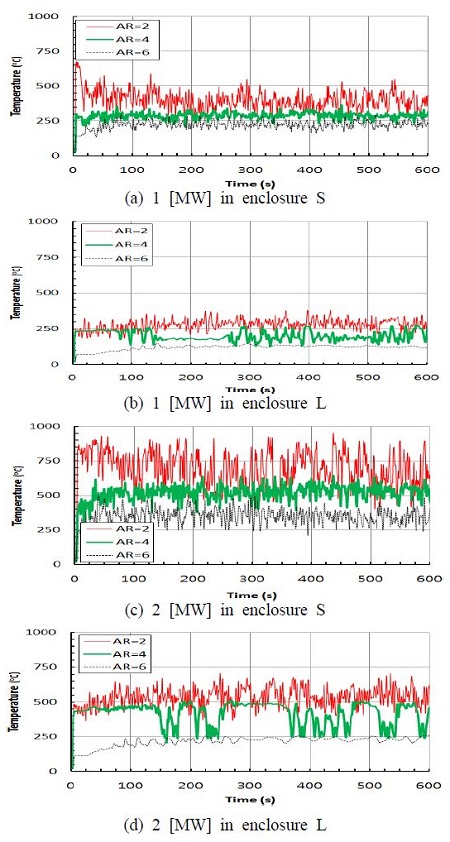
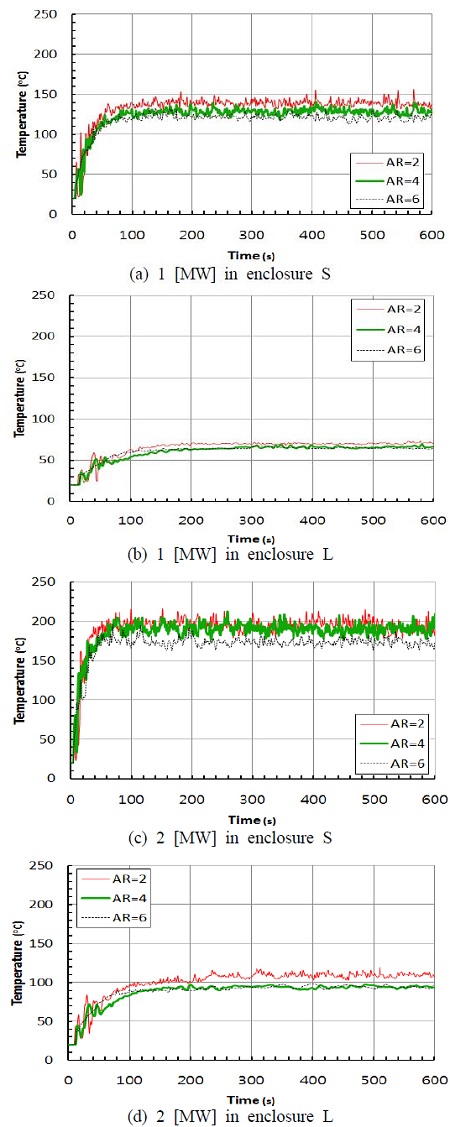
화원중심 위 천정부근에 위치한 점 C₁와 C₂에서의 온도변화가 Figure 4에 나타나 있다. 두 공간에서 모두 격자 종횡비의 증가에 따라 온도가 감소하였다. 이 경향은 1 [MW]보다 2 [MW]의 경우에 더 뚜렷하게 나타났다. 이것은 격자 Δx와 Δy의 값이 클수록 온도가 낮게 예측될 수 있으며, 화재규모가 크면 온도감소가 증가할 수 있음을 의미한다. 따라서 대규모 건축물의 성능위주설계와 같이 불가피하게 큰 값의 Δx와 Δy를 사용하는 경우에는 온도가 낮게 예측되므로 주의가 요구된다.

Figure 4:

Comparison of temperature variation with time at the center of ceiling

Figure 5에는 앞쪽문의 중앙, 바닥에서 1.8 [m] 높이에 위치한 점 P₁ 및 P₂에서의 온도변화를 비교하였다. Figure 4의 화원중심 위쪽 천장부근에 비해 종횡비 증가에 따른 앞쪽 문에서의 온도감소는 작고, 종횡비가 6일 때도 온도감소가 크지 않음을 알 수 있다.

Figure 5:

Comparison of temperature variation with time at the front door

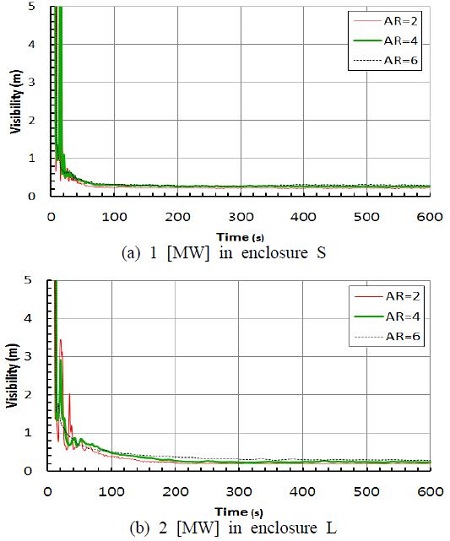
점 P₁ 및 P₂에서의 가시거리 변화는 Figure 6에 나타나있는 바와 같이 격자 종횡비의 영향이 거의 없다. 작은 공간 2 [MW]와 큰 공간 1 [MW]의 경우에도 결과가 비슷하게 나타나 그림에 제시하지 않았다. 종횡비가 크더라도 가시거리의 예측에는 문제가 없음을 알 수 있다. 그러나 가시거리가 일정치 이하가 되는 시간을 유효피난시간으로 결정하는 성능위주설계에서는 화재초기의 가시거리가 중요하므로 종횡비의 영향을 면밀하게 조사할 필요가 있다.

Figure 6:

Comparison of visibility variation with time at the front door

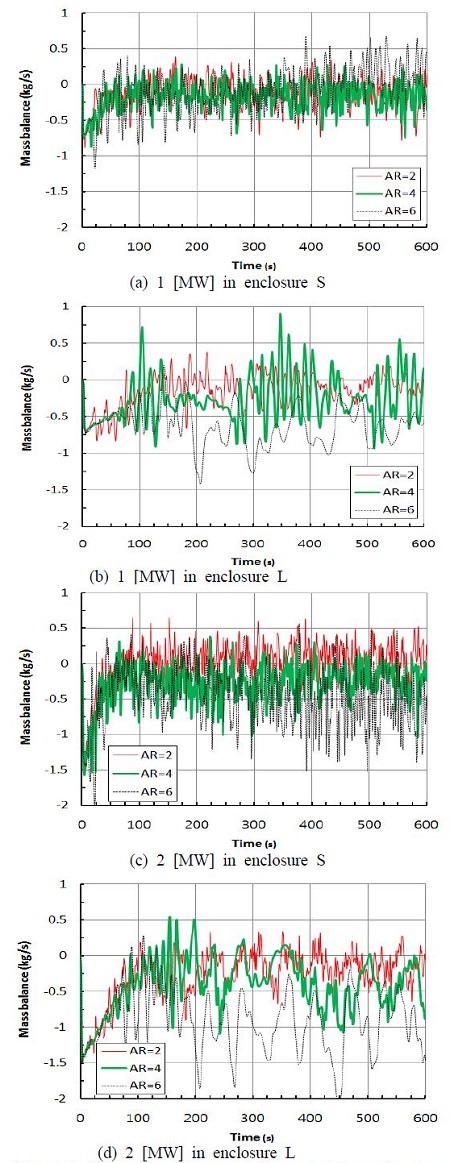
질량보존의 법칙을 만족하기 위해서는 3개의 열린 문을 통해 유출되는 질량유량에서 유입되는 질량유량을 뺀 값이 0이 되어야 한다. 그러므로 3개의 문을 통한 질량유량의 합, 즉 질량수지가 0이 되지 않고 그 절대값이 클수록 질량보존의 법칙을 더 크게 위배하게 된다. Figure 2에서 작은 공간, 1 [MW], 종횡비 AR=1일 때 질량보존의 법칙을 잘 만족하였다. Figure 7에는 두 공간과 두 값의 화재규모에 대하여 격자 종횡비에 따라 질량수지를 비교하였다. 작은 공간, 1 [MW] (Figure 7(a))의 경우에는 종횡비가 증가하더라도 질량보존의 법칙을 비교적 잘 만족하지만, Figure 7(d)의 큰 공간, 2 [MW]에서는 일 때는 종횡비가 클수록 물질수지, 즉 3개의 문을 통한 질량유량의 합이 0으로부터 멀어졌다.

Figure 7:

Comparison of mass balance variation with time through doors

이것은 공간이 크고 화재규모가 큰 경우에 종횡비가 증가하면 질량보존 법칙의 만족도가 낮아짐을 의미한다.

이상의 결과로부터 종횡비가 증가하면 온도가 낮게 예측되므로 종횡비가 3을 넘는 경우는 오차가 클 수 있음을 확인하였다. 따라서 건축물이나 선박의 실내에서 발생하는 구획화재의 시뮬레이션에서 높은 정확도가 요구되는 경우에는 수직방향 격자크기를 0.1~0.2 [m], 수평방향 격자크기는 종횡비 2, 즉 0.2~0.4 [m] 이하를 사용하는 것이 적합함을 알 수 있다.

4. 결 론

FDS를 사용한 화재시뮬레이션에 있어서 적정격자를 선정하기 위해 다양한 격자 종횡비(AR)에 대하여 조사하였다. 10 × 10 × 3 [m³]와 20 × 20 × 3 [m³]인 두 공간에 각각 1 [MW]와 2 [MW]의 폴리우레탄 화재가 발생했을 때 AR = 1~6에 대한 열방출률과 온도, 가시거리, 질량수지를 비교한 결과 다음의 결론을 얻을 수 있었다.

1) 열방출률은 종횡비와 공간의 크기 및 화재규모에 무관하게 정확함을 확인하였다.
2) AR≤5에서는 준정상상태의 온도와 가시거리가 비교적 잘 예측되었다.
3) 종횡비의 증가에 따라 화원 위 천장부근의 온도가 낮게 예측되었고, 공간과 화재의 규모가 큰 경우에 종횡비가 증가하면 질량보존의 만족도가 낮아졌다.
4) 화재 초기의 온도와 가시거리가 중요한 요소인 성능위주설계에서 AR≥3을 사용하는 경우에는 격자크기에 대한 세심한 검토가 필요함을 확인하였다.
5) 높은 정확도가 요구되는 구획화재의 시뮬레이션에는 수직방향 격자크기를 0.1~0.2 [m] 이하로 하고, 종횡비를 2 이하로 하는 것이 바람직함을 알 수 있었다.

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(과제번호 C-D-2014-0212)에 의하여 연구되었음.

References

C. W. Chiu, C. C. Wang, and C. H. Chen, “Evaluation of Downward Desmoke System in a Cleanroom”, International Journal on Engineering Performance-Based Fire Codes, 7(4), p155-173, (2005).
H. Y. Kim, D. H. Rie, and J. Y. Kim, “"Fire risk assesment for subway station according to supply and exhaust conditions”, Journal of Korean Institute of Fire Science & Engineering, 22(5), p62-69, (2008).
K. McGrattan, S. Hositikka, R. McDermott, J. Floyd, C. Weinschenk, and K. Overholt, Fire Dynamics Simulator User's Guide, NIST SP 1019, NIST, Gaithersburg, MD, USA, (2014).
W. O. Kim, J. S. Kim, and W. C. Park, “Improvement of citadel structure on board ship using FDS”, Journal of the Korean Society of Marine Engineering, 39(3), p306-311, (2015), (in Korean). [https://doi.org/10.5916/jkosme.2015.39.3.306]
W. O. Kim, J. S. Kim, and W. C. Park, “A study on the improvement of survival rate of the passengers and crews according to FDS analysis”, Journal of the Korean Society of Marine Engineering, 39(3), p312-317, (2015), (in Korean). [https://doi.org/10.5916/jkosme.2015.39.3.312]
W. O. Kim, Y. M. Chae, and C. J. Kim, “A study on the optimum capacity of citadel”, Journal of Navigation and Port Research, 36(1), p21-26, (2015), (in Korean). [https://doi.org/10.5394/KINPR.2012.36.1.21]
W. C. Park, “Selection of grid size in fire simulation for large scale buildings by using FDS”, Journal of Korean Institute of Fire Science & Engineering, 26(5), p67-72, (2012), (in Korean). [https://doi.org/10.7731/KIFSE.2012.26.5.067]
Y. J. Lee, K. C. Ko, and W. C. Park, “A study on performance-based design enforcement”, Journal of Korean Institute of Fire Science & Engineering, 26(1), p68-73, (2011), (in Korean). [https://doi.org/10.7731/KIFSE.2012.26.1.068]
K. McGrattan, S. Hositikka, R. McDermott, J. Floyd, C. Weinschenk, and K. Overholt, Fire Dynamics Simulator Technical Reference Guide, NIST SP 1018-1, NIST, Gaithersburg, MD, USA, (2014).