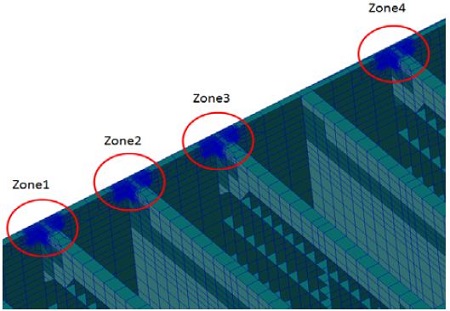
유탄성 효과를 고려한 완전통계 피로해석 프로그램 개발을 위한 기초 연구

1. 서 론

최근 신조 시장의 대형화가 지속되고 초대형 컨테이너선의 발주가 이어지면서 유탄성 현상에 대한 관심이 커지고 있다. 이는 초대형 컨테이너선이 운항 시에 화물의 적재상태로 인한 정적하중, 파랑 및 선체 동요로 인한 동적하중을 받는 것 외에도 유탄성 현상으로 인한 추가적인 하중을 받기 때문이며, 이는 선체길이가 길어짐으로 인해 선체 고유진동수가 낮아지고 파랑의 주파수 영역대로 들어와 유체-구조 상호작용을 일으키는 것을 말한다. 이러한 유탄성 현상을 스프링잉이라 하며, 하중의 크기는 파랑하중에 비해 크지 않으나 상대적으로 높은 진동수를 가져 컨테이너선의 피로강도에 큰 영향을 미치는 요소가 될 수 있다[1].

선체 유탄성 현상의 이론에 대한 초기 연구는 Bishop and Price [2]에 의하여 정립이 되었고, 이 이론은 Yousheng [3]에 의해 주파수 영역에서 3차원 선체의 선형 유탄성 운동해석 이론으로 확장되었다. 이후 2000년 초반부터 초대형 컨테이너선에 대한 시장의 요구가 시작되면서 3차원 선체 운동해석을 반영한 유탄성 해석을 수행한 연구들이 활발하게 이루어졌다[4]-[6]. 국내에서는 시간영역에서 3차원 구조해석 유한요소 모델과 3차원 선체 운동해석을 연동한 비선형 유탄성 응답에 대한 연구가 수행되었으며[7], 모형시험을 통하여 유탄성 효과로 인한 응답의 정량적인 거동을 구하려 하였다[8]. 실선 계측을 수행하여 로이드 선급은 유탄성 효과가 얼마나 피로손상에 영향을 주는지에 대한 연구를 수행하였다[9]. 이러한 대부분의 연구는 유탄성 현상을 고려하여 단면 모멘트의 응답을 구하거나 실선 계측 또는 모형시험을 통한 정성적인 분석에 관한 연구들이었으며, 유탄성 응답이 피로설계에 적용되기 위해 피로해석 기법과 어떻게 연동되어 수행되어야 하는지에 대한 연구는 거의 이루어지지 않았다. 설계에 적용되는 대표적인 피로해석 기법은 완전통계 피로해석이며, 이는 운항조건하에서 강체로 가정된 선체 운동해석과 구조해석을 수행하여 선체 피로손상을 예측하고 이를 설계에 반영하는 기법이다. 주파수영역대에서 계산이 되어 계산비용을 시간영역대에서 계산되는 기법에 비해 매우 효과적으로 줄일 수 있어 현재 많은 선급들이 각사의 경험을 반영한 완전통계 피로해석 기법을 소개하고 있다[10]-[12]. 따라서 합리적인 시간 하에서 유탄성 현상을 고려한 완전통계 피로해석 기법을 구축하기 위해서는 완전통계 피로해석 프로그램 바탕위에 유탄성 효과가 반영되도록 하는 연구가 필요하다.

이와 더불어 파랑하중과 스프링잉 현상이 복합된 유탄성 응답은 서로 상이한 주파수 영역에서 응답이 형성되어 광대역 응답으로 나타나기 때문에 이러한 광대역 응답으로부터 유발되는 피로손상을 예측하기 위해서는 별도의 연구가 수반되어야 한다. 광대역 응답에 대한 피로손상을 예측하는 관련 모델을 피로손상 모델이라 부르며, 이들 중에 Wirsching-Light[13] 모델은 낮은 광대역 응답에서 합리적인 피로손상 값을 주기 때문에 대부분의 선급 완전통계 피로해석 프로그램에 사용되고 있다. 하지만 Wirsching-Light 피로손상 모델은 높은 광대역 응답에 대해서는 과도한 피로손상 치를 주기 때문에 스프링잉으로 유발된 높은 광대역성을 갖는 유탄성 응답에 대한 피로손상을 예측하는 경우에는 부적합하다[14]. 최근에 연구된 모델들 중에 Benasciutti [15]와 Park [16]는 협대역에서 광대역성이 매우 높은 응답에 대해서도 신뢰성이 있는 결과들을 제공해주고 있으며, 특히 Park이 제안한 모델은 스프링잉 피로손상을 추정하는 로이드 선급 해석절차서의 표준모델로 채택되어있다[1]. 따라서 광대역 응답으로 인한 피로손상을 예측하기 위해서는 이러한 피로손상 모델이 완전통계 피로해석 프로그램에 도입이 되어야 한다.

본 연구의 목적은 완전통계 피로해석에 유탄성 효과를 고려하기 위한 기초 연구로서 완전통계 피로해석 기법을 소개하고 이를 구축하는 것이다. 구축된 완전통계 피로해석 프로그램의 결과는 기존의 선급에서 수행한 결과와 비교하여 프로그램의 신뢰성을 확보하였다. 향후 광대역 피로손상 모델을 구축된 완전통계 피로해석 시스템에 도입하고 유탄성 현상을 고려한 운동해석 결과와 연동시켜 유탄성 효과를 고려하면 초대형 컨테이너선의 피로설계에 사용될 수 있을 것으로 사료된다.

2. 완전통계 피로해석 기법

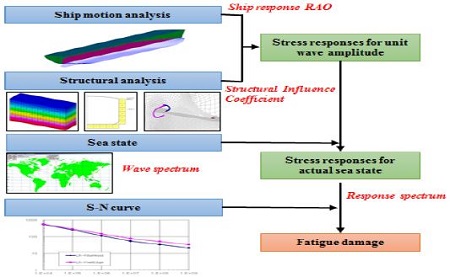
완전통계 피로해석 기법을 수행하여 선박의 피로손상을 계산하기 위해서는 Figure 1과 같이 선체운동 해석, 구조해석, 해당선박이 운항하는 해상상태 정보 그리고 S-N선도가 있어야 한다.

Figure 1:

Conceptual diagram of full spectral fatigue analysis

2.1 선체운동 해석

선체운동 해석은 강체로 정의된 선체가 다양한 형태의 단위 파고를 만날 때 선박운동에 대한 응답을 구하는 방법이며, 이는 선속(ship speed), 선수 각도(heading angle) 그리고 주파수(frequency) 별로 단위파고에 대한 선체의 응답들을 구해 준다. 설계를 위한 선체운동 해석은 주로 주파수 영역에서 수행되며, 이에 대한 지배방정식은 선체 6자유도 운동방정식인 식 (1)과 같이 나타낼 수 있다.

$\[ \sum _{j=1}^6\left[-{\omega }^2\left(M_{ij}+A_{ij}\right)+i\omega B_{ij}+C_{ij}\right]{\eta }_j=F_i,i=1...6 \]$

(1)

여기서, ω는 주파수, M_ij는 대칭 6×6 질량 행렬, A_ij는 6×6 부가 질량 행렬, B_ij는 6×6 댐핑 행렬, C_ij는 6×6 복원력 행렬이다. η_j는 6자유도 선체운동 응답벡터이며, F_i는 외력벡터가 된다.

식 (1)로부터 외력 F_i는 선체 외판에 작용하는 단위 파에 의한 외부 압력(external pressure)으로 주어지며, 이로부터 얻은 결과, η_j,는 무게중심에서의 선체운동(ship motion at COG) 응답이라는 것을 알 수 있다. 또한 외력과 선체운동 응답을 후처리하면, 단면력(sectional force), 단면 모멘트(sectional moment), 그리고 선체 가속도등을 구할 수 있다. 이러한 외력과 응답들을 통칭하여 RAO(Response Amplitude Operator)라고 하며 이를 식 (2)와 같이 간단히 복소수의 형태로 나타낼 수 있다.

$\[ H_k\left(\omega ,\theta ,v\right)=P_k+i{Q}_k,k=1,...,M \]$

(2)

여기서, θ는 선수각도이고 v는 선속이며 M은 외력을 포함한 선체운동 응답들의 총합이다.

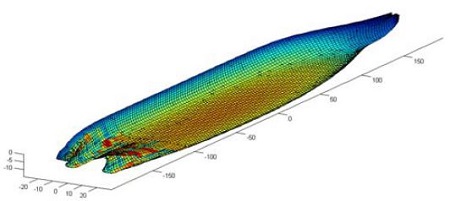
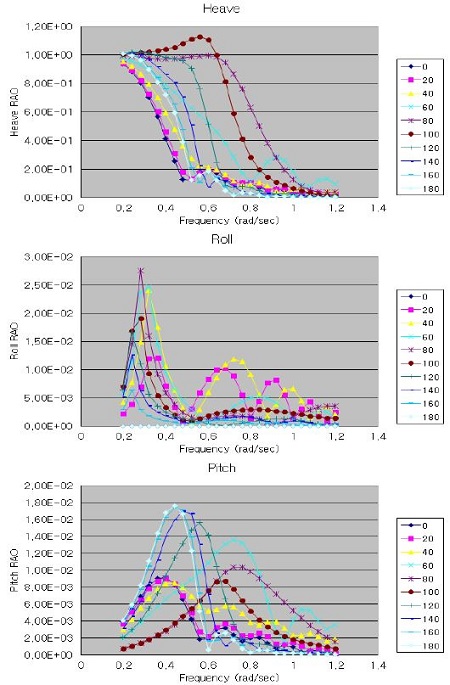
Figure 2는 선체운동 해석을 위한 선박의 수선면 하부에 대한 모델이며, Figure 3은 선체운동 해석 결과의 전형적인 예를 보여주고 있다.

Figure 2:

Hydrodynamic model

Figure 3:

Ship motion RAOs

Figure 3의 Heave운동을 보면 저주파수에서는 선체가 파고와 같이 거동을 하며 고주파에서는 파도가 선체 길이방향으로 상쇄현상이 일어나 거동을 하지 않는 전형적인 모습을 보여주고 있다. Roll운동은 약 0.3rad/sec주변의 횡파(Beam sea)에서 해당 선박의 공진이 가장 크게 나타나고, Pitch운동은 약 0.45rad/sec주변의 선수파(Head sea)에서 최대응답을 보여주고 있다. 이러한 특성들은 RAO의 형태로 완전통계 피로해석 프로그램에 적용된다. 유탄성 효과를 고려하려면 선체운동 RAO뿐만 아니라 구조응답이 RAO의 형태로 제공되는 선체 운동해석 프로그램을 이용하고 동일한 완전통계 피로해석 프로그램을 사용하면 유탄성 효과를 고려한 피로해석을 수행할 수 있다[1]. 따라서 동적인 현상이 운동해석에서 고려되었기 때문에 피로해석을 위한 구조해석은 준정적인 상태로 구현한다. 이러한 선체운동 해석 프로그램은 선급마다 자체 개발한 프로그램들을 제공하고 있으며 이를 사용하여 승인을 받는 것을 추천하고 있다.

2.2 구조해석

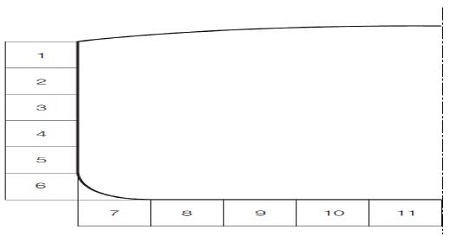
선체 강도해석을 위한 구조해석은 유한요소 모델에 설계하중을 적용시켜 유한요소해석으로 얻은 모델의 응력과 해당부위의 응력 판별식을 비교하여 판별식을 넘는 응력의 부위를 보강하는 것이다. 반면, 피로해석을 위한 구조해석은 해당 하중이 선박 일생동안 받는 해상상태 이력을 모두 고려하여 피로손상을 누적해야하기 때문에 유한요소해석으로 얻어진 응력결과를 사용하는 방법이 다르다. 다시 말해, 선체운동 해석에서 얻은 외부 압력, 가속도, 단면력 그리고 단면 모멘트가 작용했을 때 피로해석을 수행하고자 하는 해당 구조부재의 응력영향정도를 구조해석으로부터 구해야 하는 것이다. 이를 위해 운동해석으로부터 제공되는 모든 응답의 단위성분들을 각각 유한요소 모델에 하중으로 작용시키고 원하는 구조부재의 응력을 구해야 한다. 이러한 응력을 구조영향계수(Structural Influence Coefficient)라 부르며 Figure 1의 C_i를 의미한다. Figure 4는 로이드 선급의 단위 외부압력에 대한 개념도이며, 외판에 번호로 표기된 각 구역에 단위 외부압력을 작용시키고 구조해석을 수행하면 각 구역에 대한 구조영향계수를 얻을 수 있다. Figure 5는 단위 가속도에 해당되는 단위하중을 작용시키는 개념도이며 각 방향의 단위 가속도 성분에 해당되는 압력을 작용시키고 구조해석을 수행하면 각 방향의 단위 가속도에 대한 구조영향계수를 얻을 수 있다. 각 선급마다 구조영향계수를 구하는 논리는 같으나 단위하중을 작용시키는 방법은 다소 차이가 있으니 주의가 필요하다.

Figure 4:

Conceptual diagram of external pressure [10]

Figure 5:

Conceptual diagram of pressure distribution due to unit acceleration [10]

단위하중에 대한 구조영향계수(Structural Influence Coefficient) C_i를 구조해석으로부터 구한 후, 이를 식 (3)과 같이 조합을 하면 단위 파고에 대한 응력응답을 구할 수 있으며 이를 응력 RAO라고 한다.

$\[ {\Phi }_{\sigma }\left(\omega ,\theta ,v\right)=\sum _{k=1}^M{C}_k\times H_k\left(\omega ,\theta ,v\right) \]$

(3)

구조영향계수를 구하는 피로해석 구조해석 모델은 매우 높은 정도로 구조부재가 형상화되어야 한다. 일반적으로 피로수명을 구하고자 하는 위치의 유한요소 모델의 가로 및 세로 크기는 해당 위치에 접하는 모든 부재중에 최소 두께 또는 피로손상이 발생될 만한 위치의 두께를 사용한다. 이러한 상세 구조해석 모델로 얻는 응력은 선급마다 읽는 방법이 다양하며 이를 통칭하여 핫스폰 응력(Hot spot stress)라 부른다. 이 핫스폿 응력은 각 선급의 피로해석 지침서를 참고하면 알 수 있다[10]-[12].

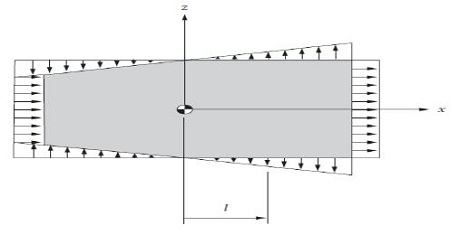
Figure 6은 선체운동 해석 결과를 선체에 작용시킬 때 발생하는 대표적인 하중의 비선형성을 나타내고 있으며 외부압력의 작용위치에 따라 하중의 응답이 다른 것을 알 수 있다. 이러한 비선형성은 외부압력뿐만 아니라 화물의 동적특성으로 인해 발생된다[17]. 이러한 비선형은 비선형 구조응답을 유발시키고 모든 응답이 선형이어야 사용이 가능한 식 (3)의 가정을 위배시킨다. 따라서 각 선급에서는 비선형 응답을 설계에 적용하기 위해 이러한 비선형 하중을 선형화하거나 비선형성을 시간영역에서 직접 계산하는 방법을 채택하고 있다[10]-[12].

Figure 6:

Nonlinearity of external pressure

2.3 해상상태

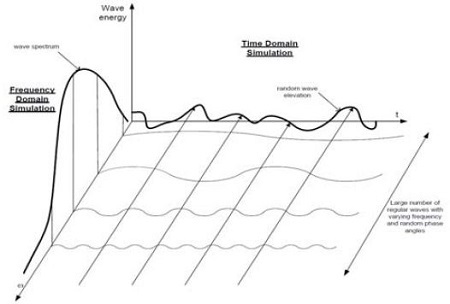
해상상태는 Figure 7과 같이 시간 축으로 보면 불규칙파의 연속이고 이를 직접적으로 고려하여 설계를 하려면 계산비용이 매우 높아진다. 반면에 이러한 불규칙파를 각각의 정규파로 분해하여 주파수영역에서 스펙트럼의 형태로 변환하면 설계적용이 용이해 진다. 다시 말해, 이 시간영역의 불규칙 해양파를 푸리어 변환으로 주파수영역으로 나타내고 각 주파수에 해당되는 정규파의 파고를 제곱하고 반으로 나누면 에너지 관점에서의 스펙트럼을 얻는데 이를 해양파 스펙트럼이라 한다.

Figure 7:

Composition of wave spectrum

과거 많은 해양학자들이 해상상태를 표현하는 이론적인 해양파 스펙트럼을 제안하였으나 대표적으로 선박에 적용되는 해양파 스펙트럼은 1966년 ISSC에서 표준 해양파 스펙트럼으로 채택한 수정된 P-M 스펙트럼(Modified Pierson-Moskowitz spectrum)이다. 이 스펙트럼은 해당 해상상태의 유의파고(Hs)와 평균파주기(Tz)만 알면 식 (4)과 같이 해양파 스펙트럼을 알 수 있다.

$\[ \mathrm{S}\left(\omega ,H_s,T_z\right)=\frac{H_s^2}{4\pi }{\left(\frac{2\pi }{T_z}\right)}^4{\omega }^{-5}\exp \left(-\frac{1}{\pi }{\left(\frac{2\pi }{T_z}\right)}^4{\omega }^{-4}\right) \]$

(4)

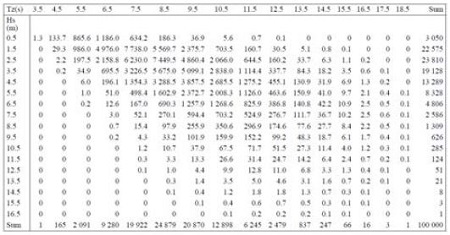
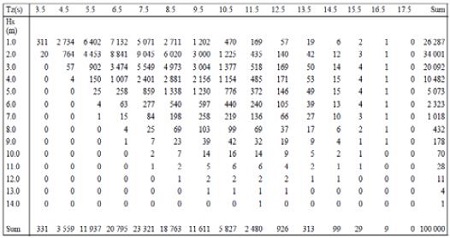
Figure 8은 가장 극심한 해상상태로 IACS의 REC34에서 제시한 북대서양 해상상태 예시 테이블이며, 강도계산을 목적으로 설계하중을 산정하는데 이 테이블이 주로 사용된다. 세로 및 가로축은 각각 유의파고와 평균파주기로 이루어져 있고 테이블의 각 셀에 해당되는 해상상태는 수정된 P-M 스펙트럼이다. 이 테이블의 각 셀 안의 숫자는 해당 해상상태가 나타난 발현횟수이다.

Figure 8:

North Atlantic sea state

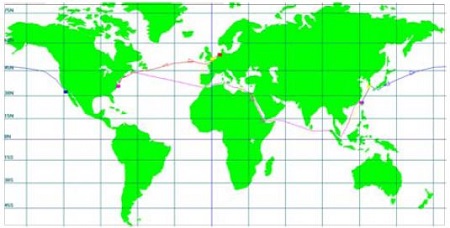
선체 피로해석을 수행하기 위해서는 운항 선박이 일생동한 경험하는 유의파고와 평균파주기 분포 및 각 해상상태의 발현 횟수를 나타내는 해상상태 분포 테이블을 알아야 한다. 이는 각 선급마다 다르게 제시하는 방법이 다르며, DnV-GL은 Figure 9과 같이 운항경로나 적재상태에 관계없이 일괄적으로 전세계 해상상태 테이블(Scatter diagram for world wide trade)을 제공하고 있으며, 로이드 선급의 경우는 Figure 10와 같이 항해 시뮬레이션(voyage simulation)을 통해 운항경로나 적재상태를 고려한 해상상태 분포 테이블을 제공하고 있다.

Figure 9:

Worldwide sea state of DnV-GL classification

Figure 10:

Voyage simulation

피로손상을 계산하기 위해서는 일생동안 경험하는 해상상태에 대한 해양파 스펙트럼으로부터 일생동안 받는 응력 응답스펙트럼을 구해야 하는데 이는 주파수 영역에서 해양파 스펙트럼과 응력 RAO를 식 (5)와 같이 합성하여 얻을 수 있다.

$\[ S_{L,\sigma }\left(\omega ,\theta ,v,H_s,T_z\right)=S\left(\omega ,\theta ,H_s,T_z\right)\bullet {\left|{\Phi }_{\sigma }\left(\omega ,\theta ,v\right)\right|}^2 \]$

(5)

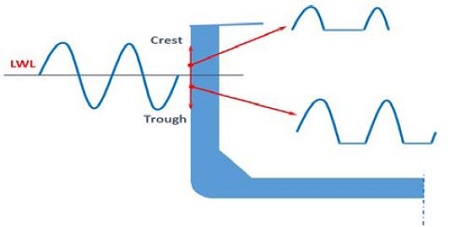
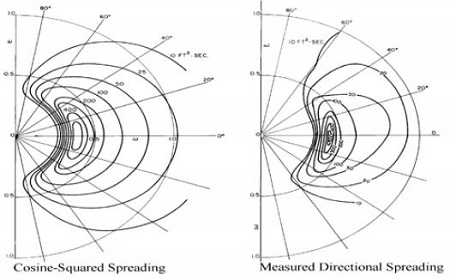
식 (5)의 스펙트럼은 해양파가 한 방향으로만 진행하는 평면파에 대한 응력 응답스펙트럼을 나타내며 이러한 파를 장파정파(Long crested wave)라고 한다. 하지만 실제 측정한 해양파는 Figure 11과 같이 여러 방향의 방향성을 가지는 단파정파(Short crested wave)이라는 것을 알 수 있다. 이러한 방향 분포를 고려하기 위해 일반적으로 코사인 제곱의 형태를 사용하며 이를 식 (5)에 적용하면 식 (6)과 같이 단파정파의 응력 응답스펙트럼을 얻을 수 있다.

Figure 11:

Comparison of short crested wave and actual measured ocean wave [18]

$\[ S_{S,\sigma }\left(\omega ,\theta ,v,H_s,T_z\right)={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{S}_{L,\sigma }\left(\omega ,\theta +\mu ,v,H_s,T_z\right)\bullet \frac{2}{\pi }\bullet {cos}^2\left(\theta +\mu \right)d\mu \]$

(6)

여기서 μ는 선수각도 θ를 기준으로 좌우 90도 방향으로 퍼져있는 해양파들을 고려하기 위한 것이다. $$ \frac{2}{\pi }$$는 cos²(θ+μ)를 $$ -\frac{\mathrm{\pi }}{2}$$에서 $$ \frac{\mathrm{\pi }}{2}$$까지 적분할 때 $$ \frac{\mathrm{\pi }}{2}$$배만큼 식 (6)의 적분값이 커지기 때문에 이를 상쇄하고자 곱한 것이다.

2.4 S-N선도

S-N선도는 일정한 응력범위(Stress Range)가 작용하였을 때 해당재료가 피로파괴를 일으키는 횟수를 로그선도로 나타낸 것이며 피로손상을 구하는데 매우 중요한 곡선이다.

이를 수식으로 표현하면 식 (7)과 같다.

$\[ \mathit{LogN}=\mathit{LogK}-\mathit{mLog}\left(\mathit{\Delta \sigma }\right) \]$

(7)

여기서 N은 파손이 발생되는 횟수이며 S-N선도이 가로축이 되며, Δσ는 응력범위로 S-N선도이 세로축이 된다. K는 재료와 용접형태 등에 따르는 피로 물성치이고, m는 S-N선도의 음의 기울기를 나타내는 피로 물성치다.

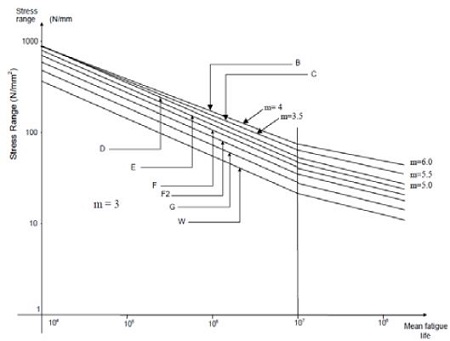
Figure 12는 영국 HSE(Healthy and Safety Executive)에서 제공하는 S-N선도이다.

Figure 12:

UK HSE S-N curve

Table 1은 영국 HSE의 S-N곡선의 피로물성치를 나타내고 있으며, m₁, K₁은 파손이 발생되는 횟수 N이 10⁷번이하일 경우에 S-N선도의 값이고 m₂, K₂은 N이 10⁷번이상의 S-N선도 값이다. 각 Class는 해당재료가 모재인지 용접재인지의 상태에 따라 구분한 것이다.

Table 1:

Fatigue properties of UK HSE S-N corve

각 선급마다 완전통계 피로해석을 위한 S-N선도를 다르게 제시하고 있기 때문에 각 선급의 피로해석 지침서를 참고해야 한다. 하지만 이들 S-N선도는 영국 HSE S-N선도에서 많이 벗어나지는 않는다.

3. 프로그램 비교 검증

로이드 선급 완전통계해석 프로그램인 FDA3(Fatigue Design Assessment Level 3)는 다른 선급과 달리 하중의 비선형성을 선형화하지 않고 일부 계산을 시간영역으로 확장하여 비선형 효과를 반영하였기 때문에 향후의 확장성이 용이하다[17]. 따라서 본 연구에서는 개발된 완전통계 피로해석 프로그램은 로이드 선급의 FDA3를 근간으로 개발하였으며 로이드 선급의 FDA3와의 피로수명 결과 비교를 통하여 개발된 프로그램의 신뢰성을 확보하려 한다.

3.1 피로해석 대상 모델

피로해석을 위한 첫 번째 대상선박은 Figure 13와 같은 컨테이너선이다.

피로해석 결과를 비교하기 위한 위치는 컨테이너선의 피로손상에 가장 민감한 해치코밍 상단으로 Figure 14과 같이 정하였다.

Figure 13:

Finite element model for containership

Figure 14:

Fatigue analysis location for containership

피로해석을 위한 두 번째 대상선박은 Figure 15와 같이 LPG운반선이다.

Figure 15:

Finite element model for LPG carrier

피로해석 결과를 비교하기 위한 위치는 Figure 16와 같이 액체운반선에 일반적으로 피로손상에 민감한 검토하는 호퍼너클 하단이다. 이는 선체 굽힘 모멘트, 외부압력 그리고 선체 내부의 탱크하중을 동시에 받는 부분이어서 피로해석 프로그램의 검증에 자주 사용되는 부분이다.

Figure 16:

Fatigue analysis location for LPG carrier

3.2 피로해석 결과 비교

본 연구의 목적은 양쪽 프로그램의 결과 값의 차이를 비교하는 것이기 때문에 식 (16)의 오차지수(Error index)를 사용하여 결과를 Table 2와 같이 평가하였다.

$\[ \mathit{EI}=\left(1-\frac{\left|\mathit{FDA}3-\mathit{developedprogram}\right|}{\mathit{FDA}3}\right)\times 100\% \]$

(16)

Table 2:

Error index for fatigue analysis results

이 결과로부터 개발된 완전통계 피로해석 프로그램이 로이드 선급 완전통계해석 프로그램인 FDA3와 일치하는 결과를 주는 것을 알 수 있다.

4. 결 론

본 연구는 유탄성 효과를 고려한 피로해석을 수행하기 위한 기초 연구로서 피로설계에 매우 중요한 역할을 하는 완전 통계 피로해석 프로그램을 구축하는 것을 목적으로 하고 있다. 컨테이너선의 대형화로 인해 발생될 수 있는 유탄성 현상에 대한 연구배경을 고찰하여 보았으며 완전통계 피로해석 프로그램을 구축하기 위해 필요한 이론적인 내용을 기술하였다.

두 가지 선종에 대해 구축된 완전통계 피로해석 프로그램을 로이드 선급 완전통계해석 프로그램인 FDA3와 비교검증을 하였으며 매우 신뢰성 있는 결과를 얻은 것을 확인할 수 있었다.

유탄성 효과를 고려한 피로해석을 수행하기 위해서는 개발된 완전통계 피로해석 프로그램에 유탄성 해석에 필요한 기술들을 추가되어야 할 것으로 사료된다. 즉, 주파수 영역이나 시간영역에서 계산된 유탄성 효과가 포함된 선체운동해석 결과들을 완전통계 피로해석에 도입하기 위한 기술적인 검토가 필요하며, 파랑하중과 유탄성 현상으로 유발된 광대역 응답에 합리적인 피로손상 값을 주는 피로손상 모델을 완전통계 피로해석 프로그램 내에 구축해야 할 것으로 사료된다.

Acknowledgments

“이 논문은 2014학년도 한국해양대학교 신진교수정착연구비 지원을 받아 수행된 연구임” 입니다.

References

• Lloyd's Register, Guidance Notes on the Assessment of Global Design Loads of Large Container Ships and Other Ships Prone to Whipping and Springing, Draft Version 1.5, Lloyd's Register, (2014).
• R. E. D. Bishop, and W. G. Price, Hydroelasticity of ships, Cambridge University Press, Cambridge, (1979).
• Y. Wu, Hydroelasticity of Floating Bodies, Ph.D. Dissertation, UK, Brunel University, (1984).
• S. E. Hirdaris, W. G. Price, and P. Temarel, “Two-and three-dimensional hydroelastic modeling of a bulker in regular waves”, Marine Structures, 16, p627-658, (2003). [https://doi.org/10.1016/j.marstruc.2004.01.005]
• S. Malenica, and J. T. Tuitman, “3D FEM–3D BEM model for springing and whipping analysis of ships”, Proceedings of the International Conference on Design and Operation of Containerships, (2008).
• K. Iijima, T. Yao, and T. Moan, “Structural response of a ship in severe seas considering global hydroelastic vibrations”, Marine Structures, 21, p420-445, (2008). [https://doi.org/10.1016/j.marstruc.2008.03.003]
• K. H. Kim, J. S. Bang, J. H. Kim, Y. Kim, S. J. Kim, and Y. Kim, “Fully coupled BEM–FEM analysis for ship hydroelasticity in waves”, Marine Structures, 33, p71-99, (2013). [https://doi.org/10.1016/j.marstruc.2013.04.004]
• S. Y. Hong, B. W. Kim, J. H. Kim, H. G. Sung, Y. S. Kim, S. K. Cho, B. W. Nam, S. K. Choi, C. Y. Lee, D. W. Lim, and M. K. Kwon, Wave Induced Loads on Ships Joint Industry Project II – Final Report, MOERI Technical Report No. BSPIS503A-2207-2, MOERI, Korea, (2010).
• N. Bakkers, J. Tong, and B. Park, “Full Scale Measurements and Fatigue Damage Assessment on a Large Container Ship”, Proceedings of the Annual Autumn Meeting The Society of Naval Architects of Korea, (2011).
• Lloyd‘s Register, Fatigue Design Assessment Level 3 Guidance on Direct Calculations, Lloyd’s Register, UK, (2002).
• Det Norske Veritas, Fatigue Assessment of Ship Structures DNV Classification Notes No.30.7, Det Norske Veritas, Norway, (2010).
• American Bureau of Shipping, GUIDANCE NOTES ON SPECTRAL-BASED FATIGUE ANALYSIS FOR VESSELS, American Bureau of Shipping, USA, (2004).
• P. H. Wirsching, and M. C. Light, “Fatigue under wide band random stresses”, Journal of the Structural Division, ASCE(American Society of Civil Engineers), 106(7), p1593-1607, (1980).
• J. Choung, K. S. Kim, J. M. Nam, J. B. Koo, M. S. Kim, Y. L. Shim, and H. S. Urm, “Study on applicability of frequency domain-based fatigue analysis for wide band gaussian process II : Wide band prediction models”, Journal of the Society of Naval Architects of Korea, 49(4), p359-366, (2012). [https://doi.org/10.3744/SNAK.2012.49.4.359]
• D. Benasciutti, Fatigue Analysis of Random Loadings, Ph.D. Dissertation, University of Ferrara, Italy, (2004).
• J. B. Park, J. M. Choung, and K. S. Kim, “A new fatigue prediction model for marine structures subject to wide band stress process”, Ocean Engineering, 76(15), p144-151, (2014). [https://doi.org/10.1016/j.oceaneng.2013.11.002]
• F. L. M. Violette, and R.A. Shenoi, “On the fatigue performance prediction of ship structural details”, Transactions of the Royal Institution of Naval Architects, 141, (1998).
• Society of Naval Architects and Marine Engineers, Principles of naval architectures, SNAME, (1988).