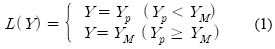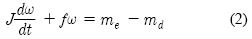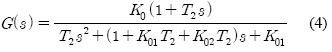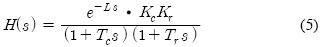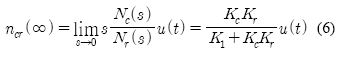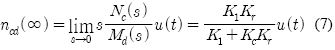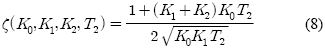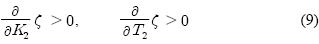A simulation module to practice hydraulic mechanical governors and its adjustment characteristics for stability
Prime movers in engine rooms inherently are much affected by the adjustment of their governors for the steady state and transient properties, consequently requiring that marine engineers shall be well familiar with the way to manage governor dials for normal operation. The hydro-mechanical governors basically have different control characteristics and adjustment parameters of stability from digital governors. The former include compensation mechanism using dash pot while the control algorithm of the latter is usually based on the PID action. This study is for configuring a simulation module to let trainees practice how to adjust dials for stability on hydraulic governors in the view that the practice by real governors and engines is time consuming and high cost for operation.
The governor module includes the adjusting points such as speed set, speed droop, needle valve and compensation pointer with engine module of 2nd order coupled. The results of simulation showed satisfactory responses as a training tool for the adjustment of control parameters.
초록
거버너의 특성은 기관 운전에 큰 영향을 미치므로 이에 대한 운전자의 조정관리가 필요하나 PID 연산을 기초로 하는 디지털 거버너와 달리 유압식 거버너는 안정도의 조정 방식에서 큰 차이가 있다. 이러한 관계의 이해에는 실물장치의 유압식 거버너로 직접 실습하는 것이 효과적이나 엔진을 구동해야 하는 등 현실적인 어려움이 있으므로 본 연구에서는 시뮬레이션 모듈의 방법으로 안정도 등의 조정 실습이 가능하도록 주요 특성을 구현하였다. 거버너 모듈에는 스피드 설정, 스피드드룹 및 니들밸브와 보상포인터 등의 조정 파라미터가 포함되었으며 2차 함수의 엔진 전달함수를 결합하였다. 이로부터 안정도에 관련되는 조정 파라미터를 가변시킬 때 얻어지는 시스템에서의 속도 및 연료량의 응답 결과를 분석한 결과 제시된 모듈이 유압기계식 거버너의 제작자가 정하고 있는 니들밸브 및 보상지침의 일반적인 조정절차를 따라 조정 실습이 가능한 특성을 나타낸다는 것을 확인하였다.
Keywords:
Hydro-mechanical governors, Compensation adjustment, Speed droop, Simulators, Adjustment practice, 유압기계식 거버너, 보상조정, 속도변동률, 시뮬레이터, 조정실습1. 서 론
유압기계식 거버너의 보상조정(compensation ad-justment)은 과도상태에서의 속도변동률 특성에 해당하는 것으로 적정한 안정도를 유지하기 위한 조정관리가 필요하다. 거버너의 종류는 디지털 거버너와 유압기계식으로 크게 나눌 수 있으며 이 중 디지털 거버너는 PID 연산에 의한 제어방식이 대부분이므로 거버너의 안정도는 포워드 비례게인과 적분계수로 조정되는 반면에 유압식 거버너는 비례 게인의 조정이 없으며 보상동작을 위한 부궤환(feedback) 신호를 과도적으로 증감시키는 방식으로 안정도 조정의 역할을 한다[1][2].
디지털 거버너에서는 일반 PID제어기에서의 조정 방식을 그대로 적용하여 안정도를 조정한다는 점에서 비교적 이해가 수월하지만 이에 대해 유압식 거버너는 대시포트에 의한 구조로 원동기 응답의 지연특성에 대응하는 구조여서 조정의 개념을 이해하기에 어려움이 더 크다.
양쪽 거버너는 제어 파라미터에 주어지는 조정점들의 명칭부터 다르므로 차이를 이해하는 데에는 거버너의 조정실습이 도움이 될 수 있으나 실물장치에 의한 실습은 엔진을 구동해야 하므로 시간과 비용 면에서 현실적이지 못하다. 한편, 해기사 교육용으로 사용되고 있는 기관실 시뮬레이터(ERS, Engine Room Simulator)나 기타 CBT 방식의 대부분은 PID 연산에 기초한 거버너로만 만들어지는 상황이므로 유압식 거버너의 조정 실습을 위해서 이들 장비들을 사용하는 것은 불가능하다는 문제가 있다.
이러한 점에서 본 연구에서는 유압식 거버너의 조정실습이 가능하도록 주요 제어파라미터를 포함하는 실습용 시뮬레이션 모듈을 구성하였으며 디젤 원동기는 연소과정과 구동축계로 구분하여 모델링하였다. 또한, 보상조정은 니들밸브(Needle valve)와 보상포인터(Compensation pointer)로 구분함으로써 유압식 거버너의 실제 조정점과 동일한 개념으로 접근하기 위한 MMI (Man Machine Interface)를 나타내었다. 실물 유압식 거버너에서 조정하는 경우 니들밸브의 개도와 보상포인터는 조정치가 작을수록 부족감쇠로 되고 이들 조정치가 클수록 과감쇠의 안정도를 나타내는 것에 대해 제시된 시뮬레이션 모듈에서 실 시스템의 경우와 동일한 형태의 응답특성을 보이는지를 확인함으로써 구성된 모듈이 실습목적에 적합한지를 살펴보고자 한다.
2. 시뮬레이션 모듈의 구성
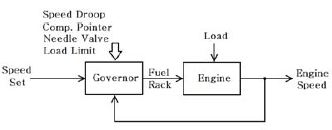
Figure 1은 시스템의 구성을 나타내는 블록선도이다. 거버너에는 속도설정(Speed set)과 피드백신호로 엔진의 속도신호가 주어지고 연료량(Fuel rack)을 출력신호로 한다. 한편, 거버너의 위쪽 화살표로 나타낸 속도변동률(Speed droop), 보상포인터(Compensation pointer), 니들밸브(Needle valve), 출력제한(Load limit) 신호는 실제 유압식 거버너에서 사용자에게 주어지는 조정점들을 나타낸다[3][4].
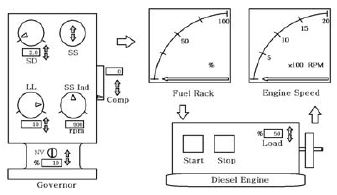
Figure 2는 Figure 1을 실습목적의 사용자 화면(MMI)으로 구성한 것이다. 엔진에는 기동(Start), 정지(Stop)의 조작버튼을 설치하였으며 또한, 엔진 부하를 조정할 수 있는 상하 양방향 표시의 화살표인 업다운 버튼(Up-down button)이 있다. 거버너 실습 기능의 특성에 국한하기 위해 엔진의 비상정지 신호 및 기타의 각종 운전 신호의 모니터링 부분은 생략하였다. 왼쪽의 거버너 모듈은 실제 거버너의 패널에서 나타나는 조정 다이얼을 형상화한 것으로 SD, SS, LL, SS Ind, NV 및 Comp는 각각 Speed droop, Speed set, Load limit, Speed set indicator 및 Compensation pointer를 나타내며 SD, LL, SS Ind의 조정점은 다이얼 모양의 화살표로 현재 값이 표시된다. 그러나 실제 조정은 업다운 버튼들의 조작으로 설정값을 선택할 수 있으며 그림에서 SS의 다이얼은 거버너의 속도 설정을 위한 손잡이일 뿐이므로 업다운 버튼만 갖는다.
거버너의 운전실습과 관련하여 조정에 따른 응답은 우측 상단의 연료량(Fuel rack)과 운전속도(Engine speed)의 계기로 확인할 수 있다.
3. 시스템 모델링
3.1 거버너 모듈
유압식 거버너의 보상(compensation)장치는 부하가 변할 때 출력신호의 부궤환을 즉시 동작시키기보다는 엔진의 응답시간을 고려하여 과도적으로 이를 지연시키는 일시적 스피드드룹(transient speed droop)의 형태로 작동한다는 점에서 탄성복원 장치에 해당한다. 이에 대해 스피드드룹으로 불리는 조정은 정상상태에서의 스피드드룹(steady state speed droop)을 나타낸다. 강성복원기구는 거버너 출력이 레버에 의해 직접 스피더 스프링의 설정 속도를 저하시키지만 탄성복원의 보상장치는 시간요소를 갖기 위한 대시포트를 설치함으로써 플로팅레버에 과도적으로 부궤환시키는 유체 커플링의 복원 구조가 된다.
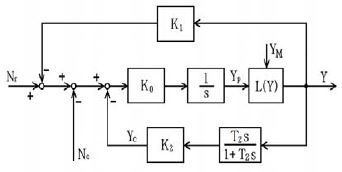
즉, 보상장치는 원심 추와 속도설정 스프링으로 이루어지는 입력 측에 거버너 출력신호를 부궤환시키는 크기가 부하 변화의 초기에 크게 작용하다가 시간이 지나면서 없어지는 구조이다. 따라서 이것의 동작은 Figure 3과 같이 1차 지연 미분요소에 의해 부궤환되는 관계로 나타낼 수 있으며 계수 K2와 시간 T2에 의해 그 정도가 조정된다. 보상장치의 부궤환 신호가 정상상태에서 소멸되는 것에 대해 스피드드룹 다이얼에 해당하는 계수 K1의 신호는 출력 Y에 비례하여 직접 속도 설정을 감소시키는 관계가 되고 있다.
여기에서 Nr, Nc, Y는 각각 설정속도, 엔진의 운전속도 및 거버너 출력인 연료 랙(Fuel rack) 신호이다. K2는 보상포인터의 계수를 위한 것이고 T2는 보상장치의 니들밸브 조정에 해당한다. 적분요소를 삽입한 것은 파일럿 밸브로부터의 유량에 대한 파워피스톤의 이동 관계를 나타내기 위한 것이다. K0은 포워드 방향의 종합 이득으로서 운전자에 의해 조정되는 계수가 아니고 거버너의 구조에 의해 고정되는 값이다.
Figure 3에서 L(Y)은 거버너의 부하제한(load limit)을 위한 리미터이다. 파워피스톤의 출력신호를 Yp라 하고 운전자가 설정하는 부하 제한값을 YM이라 하면
의 관계로 거버너 출력 Y가 제한된다.
3.2 원동기 모듈
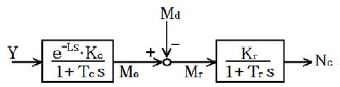
거버너가 취부된 디젤엔진에 대해 연료 연소에 의한 동력발생 부분은 시간지연이 있는 1차지연요소로 표현하고 또한, 회전계통을 1차지연요소로 나타내면 Figure 4와 같다. 여기에서 L은 시간지연의 크기이고 Kc, Tc 및 Kr, Tr는 각각 연소계통과 회전계통의 정상이득과 시정수에 해당하며 Mc, Md, Mr는 엔진의 구동토크, 부하토크 및 회전계통의 구동토크이다[5][6].
Figure 4의 계수 Kc는 연료랙(fuel rack) 입력신호에 대한 회전토크의 출력을 나타내며 시간지연 L와 시정수 Tc는 운전 회전수 nc[rpm]에 반비례한다.
또한, 엔진 축계의 관성모멘트 J [N • m • s2 / rad], 축계 마찰계수 f [N • m • s / rad], 축 회전 각속도를 w [rad / s], 운전점에서의 엔진 구동토크와 부하토크가 mc [N • m •], md[ N • m]이면
의 관계로 나타낼 수 있다. 이로부터 Tr은
와 같아진다. 따라서 Tr은 회전수와 관계없고 축계통이 갖는 고유한 일정 값이 된다.
3.3 전달함수
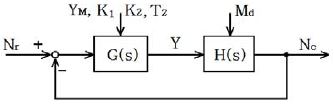
Figure 3의 거버너 부분을 전달함수 G(s)로 하고 Figure 4의 엔진 부분을 H(s)로 나타내면 시뮬레이션모듈의 결합된 블록선도는 Figure 5와 같다.
거버너의 YM, K3, K2, T2는 각각 연료제한값, 스피드드룹, 보상포인터, 니들밸브에 의한 보상시간 조정들에 해당한다. 거버너와 엔진의 블록선도로부터 G(s)와 H(s)의 전달함수는 식 (4),(5)가 된다.
여기에서 K01, K02는 각각 K01 = K0K1, KD2 = K0K2이다.
이로부터 설정속도 Nr에 대한 응답속도를 ncr(t)라 하면 입력이 단위신호 u(t)일 때 정상상태에서의 값은
로 된다. 따라서 스피드드룹 다이얼의 조정에 해당하는 K1의 값이 0이면 정상상태에서 운전 속도는 설정 속도와 같아지고 K1의 조정 값이 커질수록 속도저하(speed droop)가 증가함을 알 수 있다. 또한, 일정 설정 속도에서 부하토크 Md에 대한 운전속도를 ncd(t)라고 하면 단위신호의 부하외란에 대한 정상상태에서의 값은 식 (7)이 된다.
따라서 K1 = 0이면 정상상태에서 부하 변화가 운전속도에 미치는 영향이 없으나 K1이 커짐에 따라 부하가 증가하면 정상속도는 감소한다. 한편, 2차함수인 G(s)로부터 감쇠율 ξ을 구하면
이 된다. 이로부터 K2, T2의 조정이 ξ의 값에 미치는 영향은
의 관계가 되므로 보상포인터의 조정인 K2가 클수록 거버너 특성은 과감쇠 방향이 되고 또한, 니들밸브에 의한 시간조정 T2가 증가하여도 응답은 느리고 둔해짐을 나타낸다.
4. 시뮬레이션과 분석
4.1 모델엔진
Table 1은 시뮬레이션에 적용된 모델 엔진의 기본 제원으로서 과급기를 갖고 있으며 Pr, Nr은 정격출력과 회전수를 나타낸다. 또한, 발전기 구동의 디젤엔진에서 얻은 시운전 성적표에서 연료입력에 대한 엔진 부하의 관계를 나타내면 Table 2와 같다.
4.2 계수의 결정
K1, K2, T2는 사용자가 조정하는 계수이고 이에 대해 K0는 구조와 형상에 의한 게인 부분과 또한 파워피스톤의 적분요소가 갖는 게인을 모두 함께 포함시킨 포워드 방향의 종합게인이다. 여기에서 K0를 회전수 편차에 대한 연료 랙 출력의 관계를 고려하여 무차원 계수 5.0 으로 가정하면 거버너 출력 Y도 무차원으로 다룰 수 있어 간편해진다. 이때 사용자가 읽게 되는 연료 랙 지시치 Y′는 Table 2의 관계를 선형화 하여 나타낼 수 있으며 부하가 0[%]일 때인 연료 랙과 부하가 100[%]인 때의 연료 랙 값을 각각 Y0, Y100라 하면 Y′는
Y′ = 5.7 + ( Y100 – Y0) x Y [mm] (10)
가 된다. 또한, Y′를 [mm]의 단위가 아니고 [%]의 단위로 나타낼 때는 Y′를 Y100으로 나누어 출력하게 된다.
Kc와 Kr을 무차원으로 나타내면 1이 되고 연소계통에서의 시간지연 L과 Tc는 엔진의 형식과 회전속도에 따라 달라진다. 4행정 사이클 디젤엔진은 2회전 당 1사이클이고 또한, 과급엔진에서는 터보차저의 관성으로 인한 응답시간의 지연이 있으므로 여기서는 이들 계수를 다음과 같이 정하기로 한다.
L = Tc = 240 / nc [s] (11)
Kc와 Kr을 무차원으로 나타내면 1이 되고 연소부분의 Tc는 식 (2)의 관계를 그대로 적용하기로 한다. 한편, 회전계통의 시정수Tr을 식(3)에 의해 구하려면 관성모멘트 J와 마찰계수 f를 알아야 하나 이를 구하기 위한 제원의 확인이 쉽지 않으므로 여기서는 J / f의 값을 간접적인 방법으로 얻도록 한다. 만일, 엔진에 부하가 걸려 있지 않고 정격속도 Nr로 운전 중일 때 정지를 위하여 연료를 차단한다면 이후 회전속도는 회전계통의 관성모멘트 J의 크기에 비례하고 회전계통의 마찰계수 f에 반비례하여 감소하므로 이 경우 속도는 1차지연 계통과 동일한 형태로 감소하게 된다. 따라서 연료차단 직후 정지하기까지 소요되는 시간을 Ts라 하면 Tr = ( 1 – e-1)Ts로 나타낼 수 있으며 모델엔진의 경우 Ts가 약 10[s]가 되므로 여기서는 Tr≒6[s]로 가정하기로 한다
4.3 응답 특성
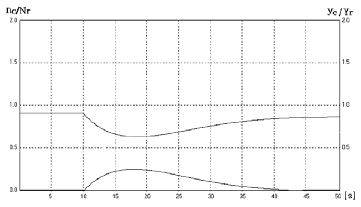
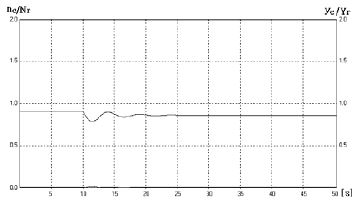
거버너의 스피드드룹에 해당하는 K1은 0.1로 조정하기로 하고 무부하 정상 운전 상태에서 정격부하 Pr의 1/2 크기에 해당하는 부하를 10[s]의 시점에서 스텝형태로 인가할 때 나타나는 속도 응답을 확인해 본다. Figure 6은 K2와 T2가 각각 3.0, 3.0[s]일 때로서 보상신호가 크게 주어진 경우이다.
수평축의 시간 t가 0 ≤ t < 10[s]인 구간은 무부하 상태에서의 속도로서 정상상태에서 일정한 속도가 되고 있다. 속도 곡선은 그래프에서 운전속도 nc를 정격속도 Nr에 대한 비율인 nc/Nr로 나타내고 있다. K1가 0.1이므로 식(6)에 의해 0.9의 일정값이 된다. Figure 6에서 아래 곡선은 보상기능의 출력 yc를 정격부하일 때의 거버너 출력 Yr에 대한 비율로 표시한 것으로서 0 ≤ t < 10[s] 구간에서 이 값은 정상상태에 있으므로 0이 됨을 보인다. 이로부터 t=10[s]의 시점에 부하가 인가되면 이 직후 아래 곡선인 보상 피드백신호가 크게 작용하면서 속도는 과감쇠 특성을 보이면서 변한다. 이로 인해 속도가 복원되기까지 35[s] 이상의 긴 시간이 소요되고 있으며 50[s] 가까이에서는 최종 속도가 식 (7)에 의해 nc × Nr의 값으로 수렴되게 된다.
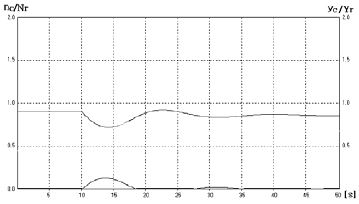
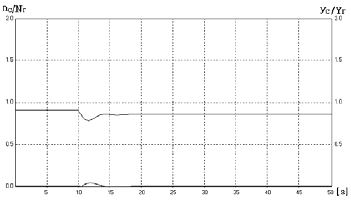
Figure 7은 보상조정을 더 작게 하여 K2 = 2.0, T2=0.5[s]인 때의 응답으로서 Figure 6에 비해 보상신호가 보다 작아지면서 속도는 상대적으로 개선된 응답을 나타낸다.
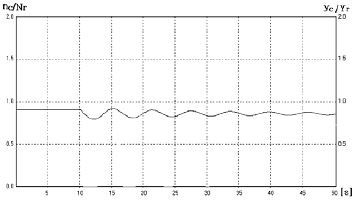
한편, Figure 8은 보상지침의 값과 니들밸브의 잠금 모두가 작아서 K2=0.1, T2=0.1[s]로 조정한 때의 응답이다. 0 ≤ t < 10[s]의 정상 구간에서 일정 속도를 겨우 유지하고 있으나 부하 인가 직후 맥동 현상은 오랜 시간 지속되고 있어서 부족감쇠의 특성이 되고 있다. 이때 아래 곡선인 보상신호는 거의 작용되지 않음을 알 수 있으며 이로 인해 불안정 방향으로의 응답을 나타낸다는 것을 알 수 있다.
Figure 9는 보상지침인 K2를 0.1로 작게 한 상태에서 니들밸브의 잠금을 증가시켜서 T2=0.5[s]로 조정한 때의 응답이다. 부하 인가 직후의 응답이 양호한 모양을 나타내고 있으며 Figure 8에 비해 부하 인가 직후 약간의 보상 신호가 작용하고 있다.
이에 대해 Figure 10은 K2가 작고 T2는 조금 더 크게 조정하여 3.0[s]인 때의 응답으로서 T2 값의 증가로 Figure 9에 비해 보상신호가 더 크게 작용하고 있다.
이 같은 응답결과를 통해 K2와 T2의 조정범위를 0에서 10으로 하는 경우 결합된 엔진의 상황으로부터 다음과 같이 안정도의 적정한 조정이 가능하였다. 즉, 보상지침 값인 K2는 0.1로 우선 작게 한 상태로부터 니들밸브 조정인 T2값을 작게 만들어가는 과정에서 T2=0.1[s] 근방에서 맥동현상이 일어났으며 이 지점으로부터 다시 반대 방향으로 T2를 증가시켜 0.5[s]이 되면 맥동현상이 곧 소멸하였다. 이 조정점의 위치에서 속도는 외란 발생 시 빠른 응답과 함께 맥동현상이 곧 소멸한다는 것이 확인되었다.
4. 결 론
디지털 거버너와 달리 유압기계식 거버너의 안정도는 보상지침과 니들밸브에 의해 조정관리가 된다. 본 연구에서는 이와 같은 유압기계식 거버너의 조정 실습이 가능한 시뮬레이션 모듈을 구성하기 위해 니들밸브와 보상지침을 포함하는 거버너 모델링을 제시하였으며 또한, 거버너와 결합되는 엔진 모델에 대해서는 시간지연이 있는 1차지연의 연소계통과 회전계통으로 구성하였다.
구성된 모듈의 속도설정과 외란에 대한 정상특성은 계통의 전달함수를 통해 예상될 수 있으나 과도특성을 포함한 응답의 확인을 위해 모델 엔진에서의 주요 계수를 정한 후 부하외란이 주어질 때 나타나는 시뮬레이션 응답곡선을 보상특성과 관련된 계수의 조합에 의해 분석하였다.
이를 통해 보상지침의 조정 값이 큰 상태에서는 항상 과도한 피드백 보상이 주어짐에 따라 부하외란에 대한 응답은 과감쇠 특성을 보였으며 니들밸브의 잠금 정도가 클수록 그 정도는 더욱 과감쇠 방향이 되었다. 이와 반대로 보상지침과 니들밸브 잠금이 작아질수록 응답은 맥동적이 되면서 부족감쇠의 모양을 나타내었다. 이것에 의해 보상지침과 니들밸브의 조정이 모두 작은 상태에서 맥동이 된다면 안정 영역으로 이동하기 위해 니들밸브를 조금 더 잠그는 쪽의 지점에서 적정한 조정점을 찾을 수 있었다.
이러한 결과는 제작자가 권장하는 유압기계식 거버너의 안정도에 대한 일반적인 조정절차와 동일한 형태가 된다는 점에서 제시된 시뮬레이션 모듈이 조정실습용으로 유용하게 활용될 수 있음이 확인된다.
References
- Electric digital governor, “http://www.scandiesel.de/downloadsht/gac010-EDG5510_DS.pdf”, Accessed February 5, (2013).
- UG-8 Governors, http://www.woodward.com/UG8-governors.aspx, Accessed March 10, (2013).
- Naeim Farouk and Liu Sheng, “Speed control systems on marine diesel engine with genetic algorithm”, International Journal of Engineering Science and Technology, 3(7), p5609-5613, (2011).
-
Le Luo, Lan Gao, and Hehe Fu, “The control and modeling of diesel generator set in electric propulsion ship”, Published Online March 2011 in MECS (http://www.mecs-press.org) Accessed, January 12, (2013).
[https://doi.org/10.5815/ijitcs.2011.02.05]

- Jianyuan Zhu, “Modeling and simulating of container ship’s main diesel engine”, Proceedings of the International Multi-conference of Engineers and Computer Scientists, 2, p1980-1983, (2008).
- Wan-Chung Lan, Takeshi Katagi, and Takeshi Hashimoto, “Quasi steady state simulation of diesel engine transient performance and design of mechatronic governor”, Journal of Marine Engineering Society in Japan, [Online]. vailable: www.mesj.or.jp, 30(1), (1995).