2MW급 풍력발전기 사이클로이드 피치감속기 설계에 대한 연구

2.1 사이클로이드 피치감속기 특징 및 구조해석

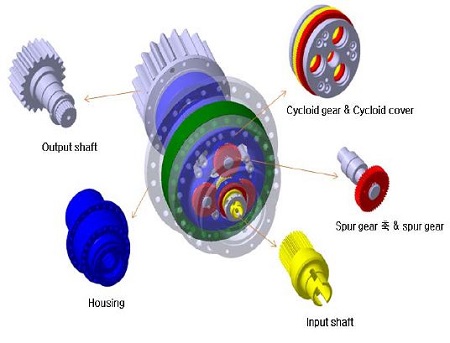
2MW급 풍력발전기용 피치 감속기는 입력축의 최대토크 28.5kNm, 입력축 회전속도 2,000rpm, 출력축 회전속도 11.594rpm, 감속비가 1/172.5이다. 피치감속기는 입력축으로 입력된 동력은 multi-mesh 평기어 쌍으로 전달되어, 이 기어를 지지하는 핀을 회전시키게 된다. 이 핀은 사이클로이드기어(cycloid gear)의 감속비에 따라서 회전속도가 결정되며, 사이클로이드 커브(cycloid cover)가 다시 출력축과 스플라인으로 결합되어 동력이 출력된다. Figure 1은 피치감속기 구조 및 부품형상을 나타낸다. Figure 1 구조를 통해 알 수 있는 것처럼, 사이클로이드 피치감속기는 2단으로 높은 감속비를 가지는 큰 장점을 가지고 있다.

Figure 1:

Pitch reducer components

피치감속기 구조해석은 하우징 부분과 하우징을 제외한 파워트레인 부분으로 나누어 해석을 실시하였다. 하우징을 제외한 파워트레인 부분은 입력축에 부하를 주어 그에 따른 시스템 전체의 응력 분포를 살펴보고, 하우징은 베어링 반력 및 Pin 반력을 예측하여 이를 하우징에 하중으로 주어 구조해석을 수행 하였다. 최대 토크가 걸렸을 때의 정격해석을 수행하며, 평가는 유한요소 해석 또는 ISO규격을 통해서 실시하였다. 유한요소해석은 부품별 묶음 해석을 수행하여 이때 나오는 베어링반력을 다른 부품의 하중조건으로 주어 수행하였다. 해석을 수행한 부품 묶음 부품 리스트는 입력축과 평기어쌍, 사이클로이드 커브, 사이클로이드 기어, 출력축, 하우징이다. 유한요소해석을 위하여 메쉬 작업은 육면체 형상과(10node) 8면체 형상(12node)을 사용하였다. 메쉬의 사이즈는 5~20mm사이즈로 생성하였다.

2.2 입력축과 평기어쌍 구조해석

2.2.1 유한요소를 통한 구조해석

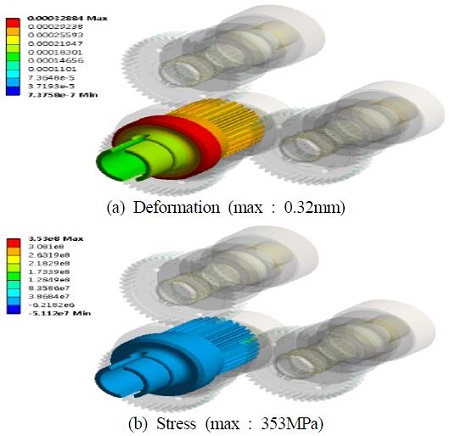
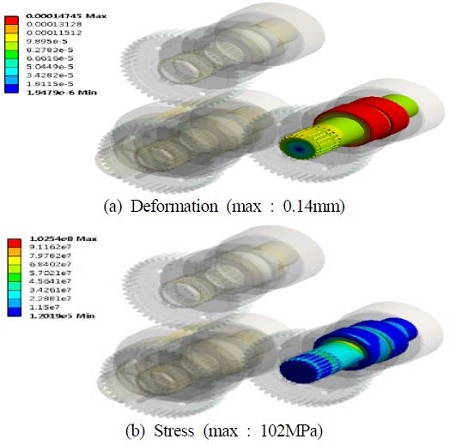
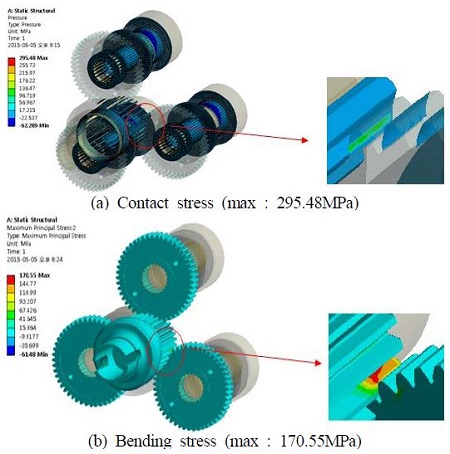
입력축에 걸리는 최대토크 28.5kNm를 하중조건으로 주었으며 기타 베어링 지지부를 지면에 고정하여 구조해석을 수행하였다. Figure 2는 입력축, 평기어 쌍의 경계조건을 나타낸다. Figure 3은 입력축에 대한 구조해석 결과를 나타낸다. Figure 3에서, 입력축은 최대 0.32mm변형이 발생하였으며, Von-misses응력을 살펴보았을 때에는 최대 353MPa이었다. Figure 4는 평기어 축의 구조해석결과를 나타낸다. Figure 4에서, 평기어 지지축은 0.14mm의 변형과, 102MPa의 응력이 발생하였다. Figure 5는 평기어의 구조해석 결과를 나타낸다. Figure 5에서, 면압강도의 경우 접촉응력(contact pressure)을 통해서 치면의 안정성을 확인하고, 굽힘강도는 최대토크를 통하여 기어의 치 뿌리 부분의 안정성을 확인 하였다. 치 굽힘강도의 경우에는 압축을 받는 쪽보다는 인장을 받는 쪽에 손상이 주로 발생하기 때문에 인장영역을 주의깊게 살펴보았다. 기어의 접촉응력(contact pressure)을 살펴봤을 때에는 최대 295MPa이 발생하였으며. 굽힘응력은 170.55MPa이 발생하였음을 확인 하였다. Figure 2∼Figure 5에서 살펴본 것처럼, 입력축과 평기어 쌍 구조해석결과 모두 안정성을 확인할 수 있었다.

Figure 2:

Input shaft & spur gear set analysis setting

Figure 3:

Input shaft analysis result

Figure 4:

spur gear shaft analysis result

Figure 5:

Spur gear analysis result

2.2.2 ISO 6336 규격에 의한 기어강도 해석

유한요소를 통한 신뢰성평가와 함께 규격 ISO 6336을 통하여 기어의 강도를 병행하여 평가하였다. 면압강도와 굽힘강도의 정적안전율과 피로안전율을 평가하였다. 아래의 식 (1)은 ISO 6336기준의 면압응력을 계산한 식을 나타낸다.

$\[ {\sigma }_H=Z_B{\sigma }_{H0}\sqrt{K_A{K}_V{K}_{\mathit{H\beta }}{K}_{\mathit{H\alpha }}} \]$

(1)

아래의 식 (2)는 굽힘응력을 계산한 식을 나타낸다.

$\[ {\sigma }_F={\sigma }_{F0}{K}_A{K}_V{K}_{F\beta }{K}_{F\alpha } \]$

(2)

입력축에 연결된 구동기어와 3개의 종동기어로 동력을 나누어 전달을 한다. 따라서 입력동력은 3등분하여 하나의 물림에서의 기어강도를 평가하였다. ISO 6336에 의해 계산된 기어의 안전율은 아래의 Table 1과 같다. Table 1에서 굽힘강도, 면압강도에 대한 안전율이 모두 안전함을 알 수 있다.

Table 1:

Spur gear safety factor

2.2 사이클로이드 커브 구조해석

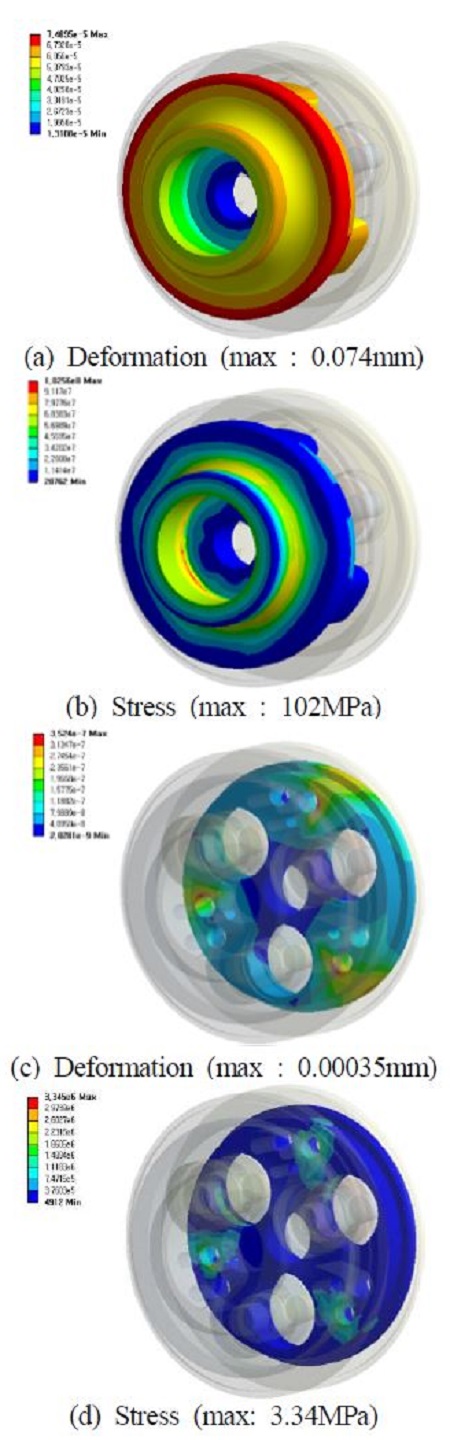
사이클로이드 커브는 출력축에 걸리는 토크를 역으로 사이클로이드 커브에 가하여 그 안정성을 확인 하였다. 베어링은 지면에 회전 조인트(revolute joint)로 고정을 하였으며, 기어의 지지 핀 부분을 고정으로 하였다. Figure 6은 사이클로이드 커브의 경계조건을 나타낸다. Figure 7은 사이클로이드 커브의 구조해석결과를 나타낸다. Figure 7에서, 커브의 앞판과 뒷판은 각각 0.074mm, 0.00035mm의 최대 변위가 발생하였으며, 응력은 102MPa, 3.34MPa이 걸림을 확인 하였다. 응력은 커브와 스플라인(spline)으로 출력축에 연결되는 부위에 큰 토크가 걸리므로 가장 높게 발생하였으며, 이외에서 커브에 사이클로이드 기어를 지지하는 핀과의 연결부위에 응력이 집중되어 있음을 확인 하였다. 커브에 걸린 응력 모두 허용치 이내의 값으로서 안정성을 확인 하였다.

Figure 6:

Cycloid cover analysis setting

Figure 7:

Cycloid cover analysis result

2.4 사이클로이드 기어 구조해석

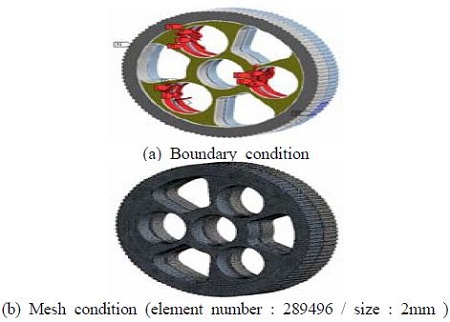
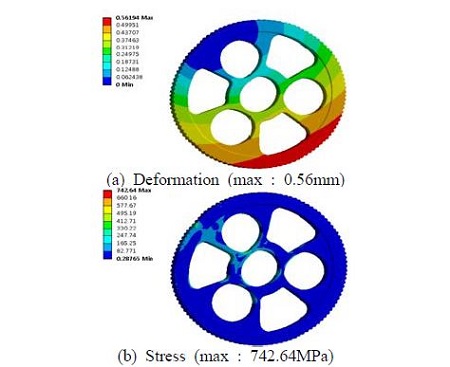
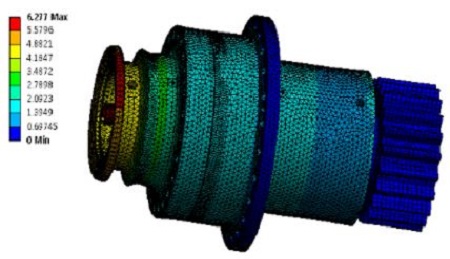
사이클로이드 기어는 입력축과 평기어 쌍 구조해석에서 나온 결과를 바탕으로 해석을 수행하였다. 앞의 해석에서 나온 반력 값을 사이클로이드 기어에 하중으로 가하였으며, 기어의 치에 고정하였다. Figure 8은 사이클로이드기어의 경계조건을 나타낸다. Figure 9는 사이클로이드기어의 구조해석결과를 나타낸다. Figure 9에서, 사이클로이드 기어는 0.56mm의 최대변위가 발생하였으며 743MPa의 최대응력이 발생하였다. 복열의 사이클로이드로 구성되어 있는 기어의 경우 두기어가 하중이 동시에 분배되기가 어려울 수 있기 때문에 하나의 기어에 하중이 집중이 될 수 있어 주의가 필요하다. 최대응력은 사이클로이드기어 몸체부분에 발생함을 확인 하였다.

Figure 8:

Cycloid gear analysis setting

Figure 9:

Cycloid gear analysis result

2.5 출력축 구조해석

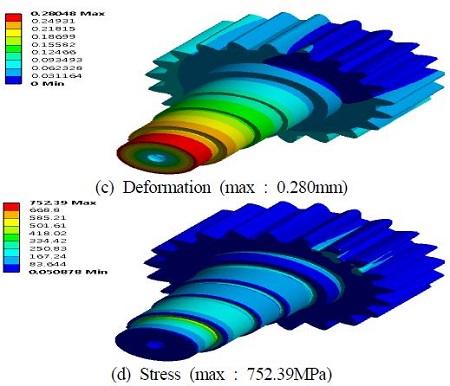
출력축은 피니언과 결합되어 있는 부품으로서 피니언의 치면을 고정으로 하였으며, 베어링은 지면에 회전 조인트(revolute joint)설정을 하였으며, 스플라인 부분에 토크를 가하여 구조해석을 수행하였다. Figure 10은 출력축의 경계조건을 나타낸다. Figure 11은 출력축의 구조해석결과를 나타낸다. Figure 11에서, 0.2804mm의 최대 변형이 발생하였으며, 752MPa의 최대응력이 발생하였다. 응력은 스플라인 부분과 축의 단차가 있는 노치 부분에서 높게 나타나고 있음을 확인 하였다.

Figure 10:

Output shaft analysis setting

Figure 11:

Output shaft analysis result

2.6 하우징 구조해석

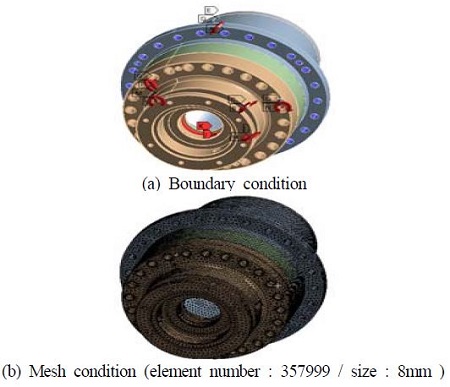
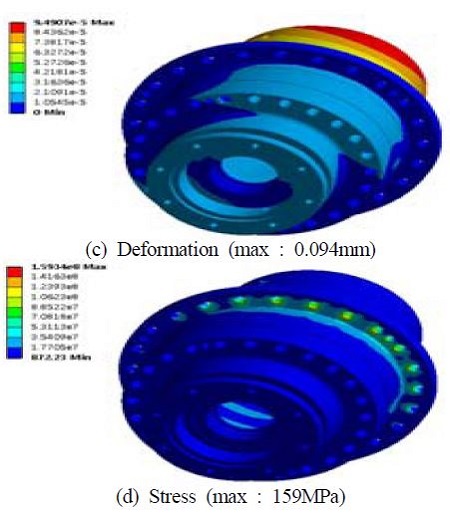
하우징에 대한 구조해석은 구조물과 결합되는 불팅(bolting)에 고정을 주었으며, 하중은 출력축 구조해석에서의 베어링에 걸리는 반력과 사이클로이드 기어해석에서 기어의 치에 걸리는 반력, 사이클로이드 커브의 베어링 반력, 입력축의 베어링반력을 가하였다. Figure 12는 하우징의 경계조건을 나타낸다. Figure 13은 하우징의 구조해석 결과를 나타낸다. Figure 13에서, 지면에 볼팅(bolting)이 지지되는 부분에 159MPa응력이 발생하였다. 변위는 출력축부분에서 약 0.094mm의 최대 변위가 발생하였다. 하우징에 걸린 응력 모두 허용치 이내의 값으로서 안정성을 확인 하였다.

Figure 12:

Housing analysis setting

Figure 13:

Housing analysis result

3.1 사이클로이드 피치감속기 고유특성 해석

풍력발전기 피치감속기 진동시스템은 식 (3)과 같이 나타타 낼 수 있다.

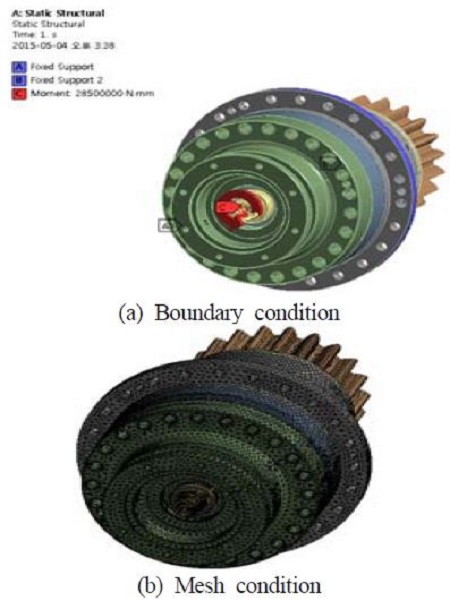
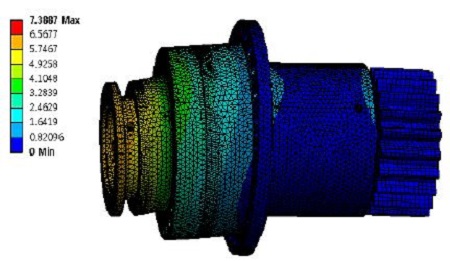
여기서 [M]은 시스템 질량 행렬, [C]는 시스템 감쇠행렬, [K]은 시스템 강성 행렬이다. q는 시스템의 자유도이다. 피치 감속기의 진동해석은 유한요소를 기반으로 수행하였다. 진동해석은 감속기에 전 하중을 주어 각 부품이 정격의 하중상태로 물려 있을 때의 상태로 하여 수행하였다. 이는 정격상태로 회전하고 있을 때의 상태와 유사하게 만들어 주기 위한 것이다. 전 하중상태를 주기 위해서, 출력축 피니언과 그라운드 지지부를 고정하였고 입력축 토크를 부여하였다. 베어링의 경우 원통형으로 단순화 하여 해석을 수행하였다. 고유치 해석을 위해서, Figure 14와 같이 메시를 나누고 경계조건을 적용하였다.

Figure 14:

Vibration analysis setting

Table 2는 2MW 풍력발전기 피치감속기에 대한 고유치 해석 결과를 표로 나타내었다. 1차 고유진동수 1427.66Hz, 2∼5차 고유진동수는 1436.93Hz, 1841.04Hz, 2226.87Hz, 2230.51Hz임을 알 수 있다.

Table 2:

Natural frequency

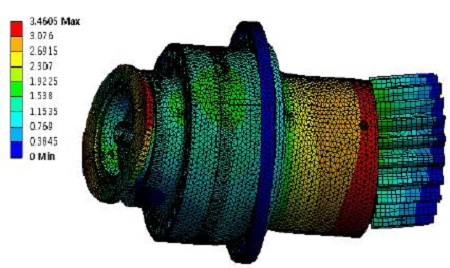
Table 2에서, 1차 고유진동수는 입력축의 변형이 크게 나타나는 진동모드를 나타낸다. 2차 고유진동수는 하우징의 변형이 크게 나타나고, 3차 고유진동수는 사이클로이드 기어와 사이클로이드 커브의 변형이 크게 나는 진동모드를 나타낸다. 4차, 5차 고유진동수는 출력축의 변형이 크게 나타나는 진동모드를 나타낸다.

Figure 15∼ 19는 1차 ∼ 5차의 고유진동수에 대한 진동모드를 나타낸다.

Figure 15:

1st mode shape (1427.66Hz)

Figure 16:

2nd mode shape (1436.93Hz)

Figure 17:

3rd mode shape (1841.04Hz)

Figure 18:

4th mode shape (2226.87Hz)

Figure 19:

5th mode shape (2230.51Hz)

3.2 사이클로이드 피치감속기 위험속도 분석

풍력발전시스템에 작용하는 가진은 크게 블레이드, 파워트레인, 발전기 부분으로 나눌 수 있다. 블레이드에서는 블레이드 개수에 비례하는 가진 주파수를 가지고 있다. 본 연구 대상은 피치감속기에 대한 위험속도해석을 하므로, 피치감속기는 질량 불평형, 기어 치합전달오차 등에 의한 가진 진동원 등이 있다. 치합전달오차가 발생하는 원인에는 크게 기어치면의 가공오차와 부하에 의한 시스템변형에 의해서 발생한다. 기어시스템의 치통과주파수(GMF : Gear Mesh Frequency)는 기어바디의 회전속도와 기어의 잇수의 곱으로 나타난다. 질량불평형은 가공오차에 의해서 편심질량이 존재하는 것으로서 축의 회전속도와 동일하다.

풍력발전시스템 사이클로이드감속기 진동/소음은 풍력발전시스템 사이클로이드감속기 가진진동수와 고유진동수가 일치 할 때 발생한다. 가진 진동수를 γ_i, i=1, 2…라 하고 풍력발전시스템 사이클로이드감속기의 고유진동수를 λ_i, i=1, 2…, N 이라 하면,

일 때 공진 떨림이 발생하는데, γ_i=C_iω_cr로 놓으면 위험속도는

가 된다. 여기서 c_i는 가진 진동수의 계수이다.

본 연구에서는 입력축, 출력축의 질량 불평형 및 기어 치합전달오차를 고려하여 가진원을 정리하였다. 가진 주파수비는 Table 3과 같다.

Table 3:

Excitation frequency ratio

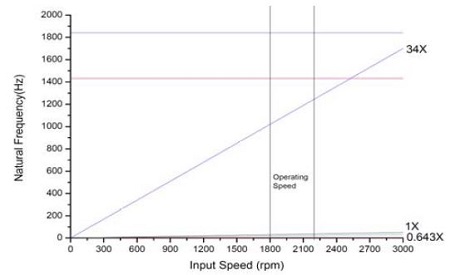
본 연구의 풍력발전기용 사이클로이드 피치감속기의 정격 운전속도는 2000rpm이며, 구동되는 작동범위를 1800 ~ 2200rpm으로 설정하여 위험속도 해석을 수행하였다. Figure 20은 질량 불평형에 의한 가진, 기어 치합전달오차에 의한 가진에 대해 위험속도 분석을 한 그래프를 나타낸다.

Figure 20:

Campbell diagram

Figure 20에서, 위험속도 범위에서 위험속도가 존재하지 않음을 알 수 있다.