Characteristics of wave propagation in a sloping-wall-type wave absorber
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The objective of this study is to observe and optimize a typical ocean environment and reduce wave reflections in the wave flume. In order to generate ocean waves in the wave flume, a combination of a horizontal piston type wave generator and wave absorbers was installed in the channel. Two probes for measuring the wave heights, i.e., wave level gauges, were used to record the continuous variation of the wave surface, the phase difference, and the maximum (crest) and minimum (trough) points of the propagating waves. In order to optimize the shape and size of the propagating waves, several absorption methods were proposed. Apart from an active wave absorption method, we used methods that involved vertical porous plates, horizontal punching plates, and sloping-wall-type wave absorbers. To obtain the best propagating waves, a sloping-wall-type wave absorber was chosen and tested in terms of the constitutive filling materials and the location and shape of the plate. This study also focused on the theoretical prediction of the wave surface, separating them into the incident and reflective components. From the results, it is evident that the wave absorber comprising a hard filling material exhibits a better performance than the absorber comprising a soft material, i.e., the wave absorber can be a strong sink to control the energy of the incoming wave. In addition, larger wave absorbers correspond to lower reflectance because a larger volume can reduce the incoming wave energy. Therefore, at constant absorber conditions, the reflectance of the wave increases as the wave period increases. Finally, the reflectance of the wave was controlled to be less than 0.1 in this study so that the wave flume can be used to simulate an offshore environment.
Keywords:
Wave maker, Wave absorber, Reflectance, Incident wave, Reflected wave1. Introduction
In marine engineering, theoretical analysis, numerical analysis, and model experiments are performed to resolve design related issues; these methods not only complement mutually but also verify each other. Currently, numerical simulations based on a computer platform are in rapid development; however, not every factor can be considered in these simulations. Hence, laboratory experiments are necessary for the optimized design of certain target models. Even though the external environmental conditions are important factors in an analysis, it is not easy to reproduce them completely in laboratory facilities such as a wave flume. In order to make a proper measurement in this regard, a variety of equipment is required. One of the difficult tasks in laboratory experiments is the reproduction of offshore environments such as general periodic waves. When a wave is generated at one end of the wave flume, the propagating wave moves toward the other end such that a reflective wave is produced. This phenomenon complicates the analysis because these waves superimpose, separate, and merge with each other. Usually, these multi-reflection waves should not occur in the laboratory, which is not possible in real ocean environments. Therefore, in order to reproduce the ocean environments effectively, an optimized design of a wave absorber is necessary.
In this study, the behavior of the propagating waves, which is separated into incident waves and reflected waves, was observed. The waves in the lateral direction where the flow velocity is relatively less than the main propagating waves could be assumed negligible based on previous studies. This method was developed by Healy to estimate the reflection of regular waves by measuring the maximum and minimum amplitudes of a standing wave envelope. In addition, this method requires a wave gauge moving slowly along a line parallel to the direction of wave propagation in the wave flume. Even though this method is simple and convenient for analysis, the error was substantially large because of the continuously reflected waves[1]. On the other hand, there are alternate methods for separating the incident and reflected waves; one method uses two fixed wave gauges for measuring two wave heights and one wave phase, and another method uses three fixed wave gauges for measuring three wave heights and two wave phases[2][3]. Considering the limitations of a wave flume, the method suggested by Goda and Suzuki seems to be appropriate for our test condition[4]-[6].
In this experiment, wave generation was studied using a wave flume with a wave absorber. Waves were generated using a piston arrangement propelled by a stepping motor. A variety of wave absorber models with high accuracy is covered in this paper. The wave absorber was mainly filled with a nylon fabric mesh material (nylon mesh is free from corrosion, wear and tear, and has a long life) and covered with a thin stainless absorber plate. The filler was located inside the volume formed by the wave absorber plate and the wave flume. Three different arrangements were made by varying the angle of the absorber, the number of absorber plates, and the location of the absorber plate. The entire study was done using electronic wave gauges and a control unit, which was connected to a personal computer for data acquisition. With these facilities, reflectance and wave height variation on the free surface under several wave periods were evaluated.
2. Design of Laboratory Experiments
2.1 Experimental set up of wave flume
The experiment was carried out in a wind-wave flume of length 5 m, width 0.4 m, and height 0.85 m and a wind tunnel cross section of 400 mm × 400 mm (Figure 1). A piston type wave generator was located at one end of the tunnel with a five-phase stepping motor (PK596AWM) connected to it. A wave absorber was installed at the other end of the tunnel. A blow-down type wind tunnel has a maximum speed of 35 m/s and not used in this measurement, but the combination of wind and wave will be one of the interesting studies for further works.
Two wave gauges (KENEK Wave Height Meter CH-606) were used in the experiment, and the distance between them is denoted by ∆l where 0.1L < ∆l < 0.5L (L is the wavelength), so that the incident waves and the reflected waves are distinguished clearly. The two wave gauges were installed depending on the experimental conditions, but their positions were suitably chosen in the direction of wave propagation, which is considered as a different wave zone to measure the maximum and minimum wave heights while evaluating the incident and reflected waves. Waves were generated by a combination of the piston cylinder assembly and a stepping motor controlled by an AVR 128 electric circuit and a visual basic program. The output probes of the wave gauges were connected to a data logging unit (NI USB-9151), which stores the analog signal and transfers the data to a computer hard disk. The schematic diagram of the setup is shown in Figure 2.
2.2 Wave theory and reflectance (KR)
It is assumed that a wave paddle helps the waves propagate forward in a wave flume, and the waves are reflected back at the other end. Then, the reflected waves move back toward the wave paddle and are reflected again. The re-reflected waves propagate forward again and this process is repeated until the multi-reflected waves are fully attenuated. The wave train in the positive direction is called the incident waves and that in the negative direction is called the reflected waves. The amplitude of the incident waves is denoted by aR and the amplitude of the reflected waves by aR[2]. Wave modeling in this condition is summarized from equation 1 to equation 13 to obtain the incident and reflected waves followed by appropriate curve fitting. Two different waves can be formulated as follows:
| (1) |
| (2) |
| (3) |
where ηI and ηR are incident and reflected waves, respectively, L is the wavelength and k is the number of 2π/L.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
The observed profiles of composite waves will be:
| (10) |
| (11) |
In the equation above, all the constant can be calculated and X1, Y1, X2, Y2 can be calculated by Fourier analysis.
| (12) |
| (13) |
Therefore, the reflectance (Kr) can be calculated by using equation (3).
3. Results and Discussion
3.1 Effect of wave absorber on wave reflectance
Figure 3 (a) shows the variation in the calculated reflectance against different locations of the wave absorber plate (the angle of the absorber plate remains constant α=β=γ). Figure 3 (b) shows that the wave absorber with a larger volume exhibits lower values of reflectance because of the high absorption of wave propagation in the flume. The reflectance increases with increasing wave period. As a result, the change in the location of the frame from 0.95 m to 1.15 m had no significant effect on the reflectance. However, when the frame was moved to 1.35 m (further upstream), the reflectance was substantially reduced to less than 0.1 and remained stable. In this study, the wave absorber exhibited the lowest reflectance and remained stable when the absorber frame was at 1.35 m. The lowest reflectance was 0.035 at a non-dimensional frequency of 0.9.
Figure 4 (a) shows the variation of the angles of the absorber plate (37°, 45°, and 60°) with the volume enclosing the water inside the mesh fixed at 0.13 m2. As shown in Figure 4 (b), the best absorption was observed at an angle of 37°, whereas, the other two cases had a relatively high values of reflectance. The reflectance attained a minimum value when the non-dimensional frequency was 1. The reflectance increased when σ2h/g was between 1 and 1.32 and decreased thereafter. When the angle reduced to 37°, the reflectance substantially reduced less than 0.1 and remained stable. An additional experiment was carried out to show that when the plate angle is less than 37°, the reflectance obtained would be less than 0.1. Therefore, at a fixed volume, reducing the angle of the wave absorber plate can increase the wave absorption and produce a stable reflectance. In Figure 3 (b), to find out the possible effect of the volume of the wave absorber, the angle of the wave absorber frames was set to be approximately 37°. Further studies will be carried out to confirm whether these two parameters have an isolated effect or a coupled effect on the reflectance coefficient.
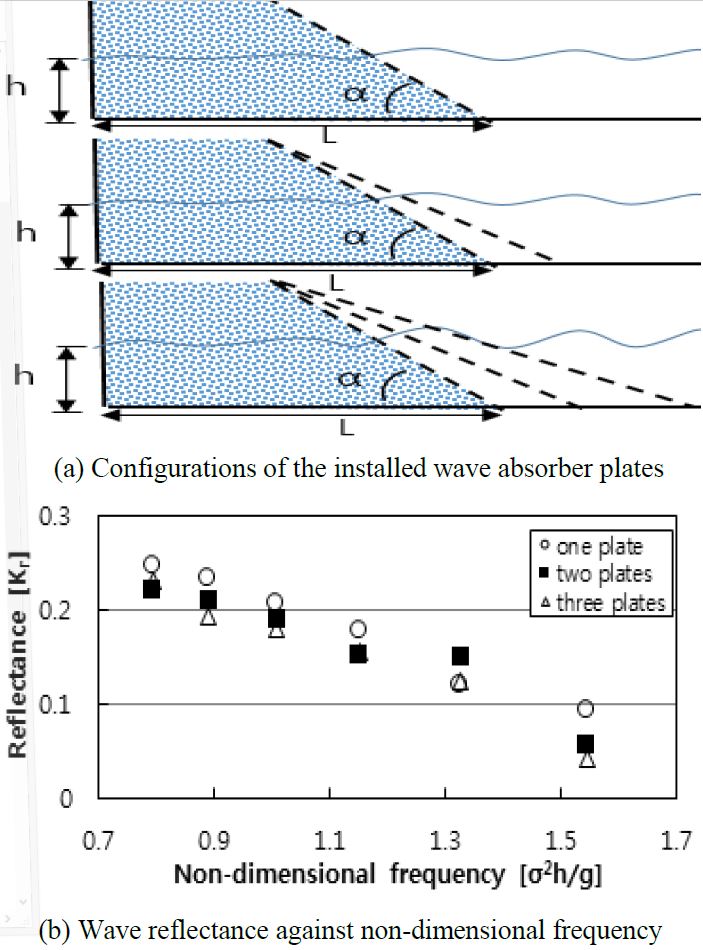
Figure 5 (a) shows the configurations of the installed wave absorber plates. In this case, the number of wave absorber plates in the wave flume was varied, i.e., single, double,and triple absorber plates, at a constant filler volume.As shown in Figure 5 (b), the wave reflectancevalues are scattered. As the number of absorber platesincreases, the overall reflectance decreases. In addition, as the non-dimensional frequency decreases, the reflectance increases. In comparison, the results are in good agreement even with different combinations of the absorber plates. While using a single absorber plate, the highest reflectancewas approximately 0.25 at σ2h/g = 0.8. On the other hand,while using triple absorber plates, the lowest reflectance was0.045 at σ2h/g = 1.55. A similar reflection distribution ineach case indicates that the absorption of the wave absorber is mainly dependent upon the fillers, whereas the number of absorber plates did not substantially influence the variation in wave reflectance.

Reflectance coefficient against non-dimensional frequency with a fixed angle of 37 at different locations of wave absorber plate
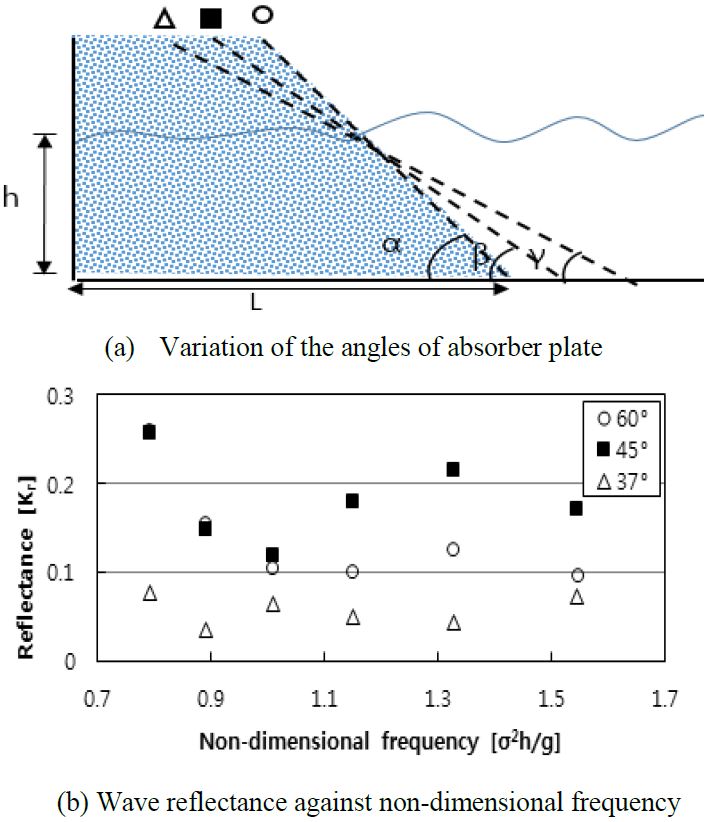
Reflectance distribution against non-dimensional frequency with a certain volume (0.13m2) for different angles of plate.
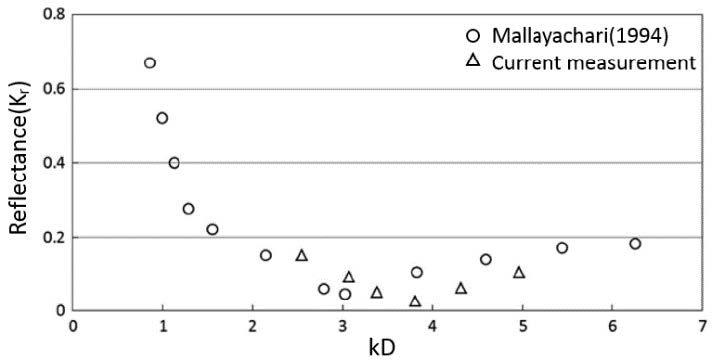
3.2 Comparison with the existing study
In order to evaluate our experimental results, a comparison has been made between the current work and a numerical result of Mallayachari [8] on the reflectance (KR) as shown in Figure 6. In his work, the porosity and wall slope of the wave absorber were set to 0.5 and 45°, respectively. For a feasible comparison, kD is used in the abscissa instead of the non-dimensional frequency (σ2h/g) where D is the width of the wave absorber. Both the results indicate that the wave reflectance decreases and attains a minimum value of approximately 0.46 at kD = 3 (numerical) and 0.03 at kD = 3.8 (experiment). As shown in Figure 6, the results are in good agreement within a certain range. In addition, most of the reflectance data are less than 0.1. Therefore, a sloping-type wave absorber in a short-distance wave flume can be used for further studies.
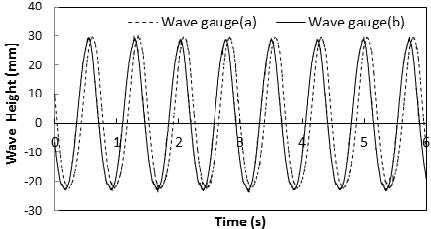
3.3 Wave height variations with and without wave absorber
Figures 7 and 8 show a typical example of the sinusoidal wave generated by the wave maker in the transverse direction of the wave flow. The two wave gauges were placed at a certain distance((Δl)), and the recorded data is shown in Figure 7. It can be observed that the differences in wave amplitude at the two measurement stations are within 1 mm, which is negligible, and the phase difference seems to be due to the separation distance. It can also be observed that only one regular wave is propagating through the flume. In other words, the optimized wave absorber suppresses most of the reflected waves. As shown in Figure 8, the wave generator operation cuts in and cuts off at around 0 s and 28 s. While using the absorber, the maximum wave height substantially reduces to approximately 11 mm in a regular pattern. When the motor stops instantly, the wave height becomes stationary. On the other hand, without the absorber, the reflective waves were generated at the other end even though the wave generator ceased for a certain period. Therefore, the designed absorber significantly reduces the reflected waves in the laboratory-scale wave flume.
4. Conclusion
Wave generation was studied using a combination of a wave flume and an absorber in laboratory scale. The generated wave was measured by two different wave gauges. The measured data was evaluated based on the wave theory and reflectance parameters at two points separated by a distance. From the study, it is clear that there is a change in the wave amplitude at the receiving end and then in the generated end. A wave absorber is a strong sink to control the energy of the incoming wave. The reflectance increases with increasing wave period. The thickness of the wave absorber has a substantial effect in absorbing the reflected wave. In this study, when the thickness of the wave absorber is 1.35 m, the wave absorber has the lowest reflectance and remains stable. The reflectance coefficient varies with the varying angle of the absorber plate because of the volume handled by it. In this preliminary experiment, wave generation was successful but further experiments should be conducted for an appropriate absorber. In order to make further progress based on this configuration, an absorber with various porosities of nylon mesh and different incident waves such as irregular waves will be designed and built in the water flume, which is necessary to be considered for the optimized design of a wave absorber.
Acknowledgments
This work was supported by a 2-Year Research Grant of Pusan National University.
References
- J. J. Healy, “Wave damping effect of beaches”, Proceedings of the Minnesota International Hydraulics Convention, p213-220, (1952).
- Y. Goda, Y. Suzuki, “Estimation of incident and reflected waves in random waves”, Proceedings of the fifteenth Conference on Coastal Engineering, ASCE, New York, p828-865, (1976).
- C. J. Galvin, Wave Height Prediction for Wave Generators in Shallow Water, U.S. Army, Coastal Engineering Research Center, (1964).
- L. Greslou, and Y. Mahe, “Etude du coefficient de reflection dune sur un obstacle constitue par un plan incline”, Proceedings of the Fifth Conference on Coastal Engineering, p68-83, (1954).
- E. F. D. Masard, and E. R. Funke, “The measurement of coexisting random wave energy”, Proceedings of the fifteenth Conference on Coastal Engineering, ASCE, New York, (1980).
-
P. A. Madsen, “Wave reflection from a vertical permeable wave absorber”, Coastal Engineering, 7(4), p381-396, (1983).
[https://doi.org/10.1016/0378-3839(83)90005-4]

-
S. H. Kwon, W. M. Moon, and H. S. Lee, “Experimental and numerical studies on the development of a new wave absorber”, Ocean Engineering, 30(1-2), p185-203, (2003).
[https://doi.org/10.1016/S0029-8018(02)00019-7]

-
V. Mallayachari, and V. Sundar, “Reflection characteristics of permeable seawalls”, 23(1-2), Coastal Engineering, p135-150, (1994).
[https://doi.org/10.1016/0378-3839(94)90019-1]

-
R. A. Dalrymple, M. A. Losada, and P. A. Martin, “Reflection and transmission from porous structures under oblique wave attack”, Journal of Fluid Mechanics, 224, p625-644, (1991).
[https://doi.org/10.1017/S0022112091001908]