[ Article ]

Journal of the Korean Society of Marine Engineering - Vol. 39, No. 8, pp.807-812

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Oct 2015

Received 12 Oct 2015 Revised 21 Oct 2015 Accepted 21 Oct 2015

DOI: https://doi.org/10.5916/jkosme.2015.39.8.807

Thermal properties of latent heat storage microcapsule-water slurry

Soo-Beom Mun^†

Correspondence to: ^† Training ship of Kunsan National University, 588 Daehak-ro, Gunsan, Jeonbuk 573-701, Korea, E-mail: sbmoon72@kunsan.ac.kr, Tel: 063-469-1727

Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

A microcapsule water slurry is a latent heat-storage material having a low melting point. In this study, the thermal properties of a microcapsule water slurry are measured. The physical properties of the test microcapsule water slurry, i.e., thermal conductivity, specific heat, latent heat, and density, are measured, and the results are discussed for the temperature region of solid and liquid phases of the dispersion material (paraffin). It is clarified that Eucken’s equation can be applied to the estimation of the thermal conductivity of the microcapsule water slurry. Useful correlation equations of the thermal properties of the microcapsule water slurry are proposed in terms of the temperature and concentration ratio of the microcapsule water slurry constituents.

Keywords:

Thermophysical property, Cold heat storage, Latent heat, Microcapsule slurry, Paraffin

1. Introduction

Recently, much attention has been paid to the investigation of the usage of slurry-type latent heat-storage (phase-change material) systems [1]. This type of latent heat-storage system can substitute a traditional sensible (water) heat-storage system. The benefit of a low-temperature phase-change material (solid-liquid phase) in water is that it increases the amount of heat transmitted and heat-transfer coefficient by the churning effect [2]. The latent heat-storage material and water can be mixed by dispersion-mixing methods such as microencapsulation [3]. As phase-change microcapsules have a complex construction, only a few studies on the thermal properties of phase-change microcapsules have been conducted. The present study considers a microcapsule (paraffin, freezing point T_m = 278.9K, latent heat L = 164 kJ/kg, as the phase-change material) water (continuous phase) slurry as the experimental latent heat-storage material.

The Density, specific heat, latent heat, and thermal conductivity of the microcapsule water slurry were measured using a specific-gravity meter, a water calorimeter, a differential scanning calorimeter (DSC), and a transient hot-wire method [4][5], respectively, in the temperature range over the solid-liquid phase change. Eucken’s model was applied to estimate the thermal conductivity of the microcapsule water slurry.

2. Feature of Test Microcapsule Water Slurry

Paraffin, which is a cold latent heat-storage material, is an insoluble oil [6]. This type of insoluble oil is dispersed in water by using capsulation, i.e., microencapsulation is used to obtain a homogeneous microcapsule water slurry [8].

Figure 1 (a) shows the external appearance of the test microcapsule water slurry (C_mi = 40.8wt%). The microcapsule water slurry has a white color and good fluidity. A microphotograph (2000 magnification of microcapsule water slurry) is shown in Figure 1 (b). Figure 1 (b) illustrates the homogeneous dispersion of spherical microcapsules in water.

Figure 1:

Microcapsule water slurry

3. Estimation of Specific Heat and Latent Heat

Figure 2 indicates the water calorimeter used for the measurement of specific heat. A water calorimeter was used because paraffin gets supercooled easily. The latent heat of the microcapsule water slurry was measured by a DSC, which can also simultaneously measure the melting point of the microcapsule water slurry.

Figure 2:

Cut view of water calorimeter

3.1 Measuring Device and Procedures for Specific Heat and Latent Heat Measurement

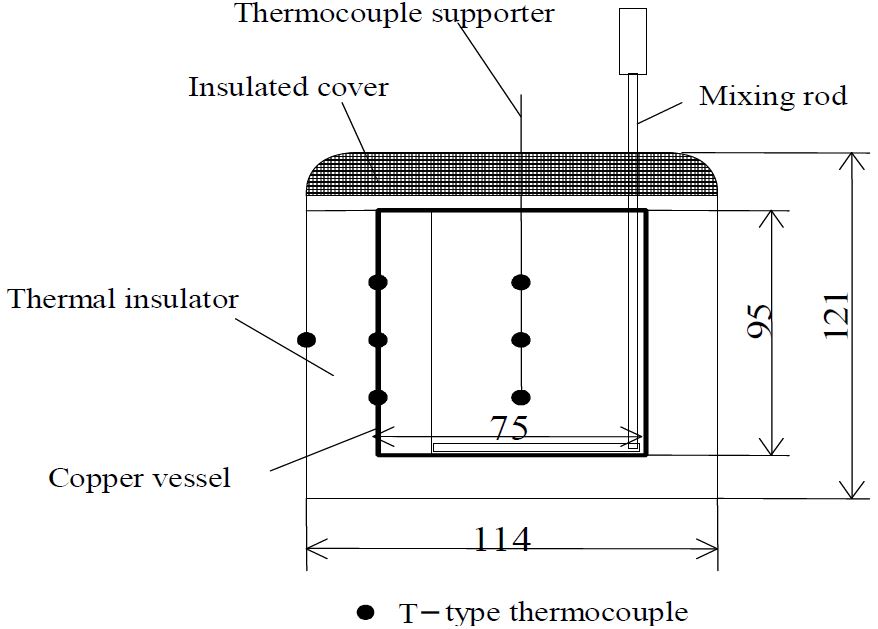
The specific heat of the microcapsule water slurry Cp_mi was measured using the water calorimeter as mentioned above. The measuring process was as follows. The temperature of the water (M_w = 80 g) in the calorimeter (copper vessel M_c = 80.96 g, mixing rod M_m = 12.53 g) was controlled by a temperature control bath. Subsequently, the test microcapsule water slurry, whose temperature is 5.0–6.0K higher than the initial water temperature in the calorimeter, was placed inside the water calorimeter. The specific heat of the microcapsule water slurry was calculated from equation (1), which is derived from the heat capacities of water (M_w X C_pw), copper vessel W_c, and mixing rod W_m, and the heat loss Q_l resulting from the temperature difference between the test sample and the environment temperature.

C p m i = M w × C p w + W c + W m × T f i - T w s - Q l M e × T e s - T f i

(1)

where T_fi is the equilibrium temperature of the microcapsule water slurry and the water mixture, T_ws is the initial temperature of the water in the calorimeter, and Q_l is the heat loss from the water calorimeter. The heat loss from the water calorimeter Q_l was estimated from the temperature variation of the cold water in the water calorimeter [5]. The accuracy of the mass weight and temperature measurements were within 土0.1% and ±0.4%, respectively. The ratio of the heat loss Q_l to the total heat transfer in the calorimeter was less than 4.0%; thus, the total accuracy of the water calorimeter is estimated to be within ±5.0%. The specific heat of water measured by the present water calorimeter shows good agreement with the reference value [7] with an accuracy within 土5.0%.

A DSC was used for measuring the latent heat and melting point of paraffin (dispersed phase-change material). The test section of the DSC was mounted into the temperature control bath (capacity 50 × 50 × 50 cm, temperature range T = 253–298 K, temperature control accuracy ±0.1 K). In order to completely freeze the paraffin, the temperature of the test microcapsule water slurry was decreased to 263 K by the temperature control bath. Then, DSC measurements were taken when the microcapsule water slurry temperature reached 274K in order to melt the water as a continuous phase.

The latent heat of the microcapsule water slurry was measured under a heating rate V_h of 5.0 K/min, and the mass of the sample M_e was 5.0–6.0 mg. The total accuracy of the measurement was estimated to be within ±2.0% in consideration of the heat supply of the electric heater. The temperature measurement accuracy was ±0.1% and the measurement accuracy of the mass weight of the sample was ±0.5%. The latent heat of water and indium (purity 99.99%) were measured by the present DSC, and the measured values coincide with the reference values [9] with an accuracy within ±2.0%.

3.2 Measuring Results and Discussion of Specific Heat and Latent Heat

Figure 3 shows the relationship between the specific heat of the microcapsule water slurry Cp_mi, water Cp_w, and paraffin Cp_p, and temperature T. The specific heat of paraffin is almost constant Cp_p= 1.8 [kJ/(kg·K)] in the temperature region of the solid phase (T < 278.9 K). In contrast, the specific heat of paraffin in the liquid phase (T > 278 K) increases with temperature T, and its value is greater than that in the solid phase (T < 278.9 K). The specific heat of the microcapsule water slurry Cp_mi shows variation between the solid and liquid phases (melting point T_m = 278.9K). The specific heat of the microcapsule water slurry in the liquid phase is greater than that in the solid phase. The specific heat of the microcapsule water slurry Cp_mi decreases with an increase in paraffin concentration C_p. This tendency of the specific heat of the microcapsule water slurry could be caused by the fact that the specific heat of paraffin Cp_p has a smaller value than that of water Cp_w. The specific heat of the wall material is constant Cp_me =1.67 [kJ/(kg·K)]) in the temperature range of T = 273–293 K[9]. An additional properties equation can be applied to the calculation of the specific heat of the microcapsule water slurry, as shown in equation (4), by using the reference values of the specific heat of water Cp_w[8], the specific heat of paraffin in the solid phase Cp_p = 1.8 [kJ/(kg·K)], and the specific heat of paraffin in the liquid phase, which can be calculated from equation (2).

Figure 3:

Relationship between specific heat and temperature

C p p s = - 5.85 × 10 - 3 T + 3.69 273 K ≺ T ≺ K

(2)

C p m i = C p p C p + C p w C w + C p m e 100 - C p - C w 100

(3)

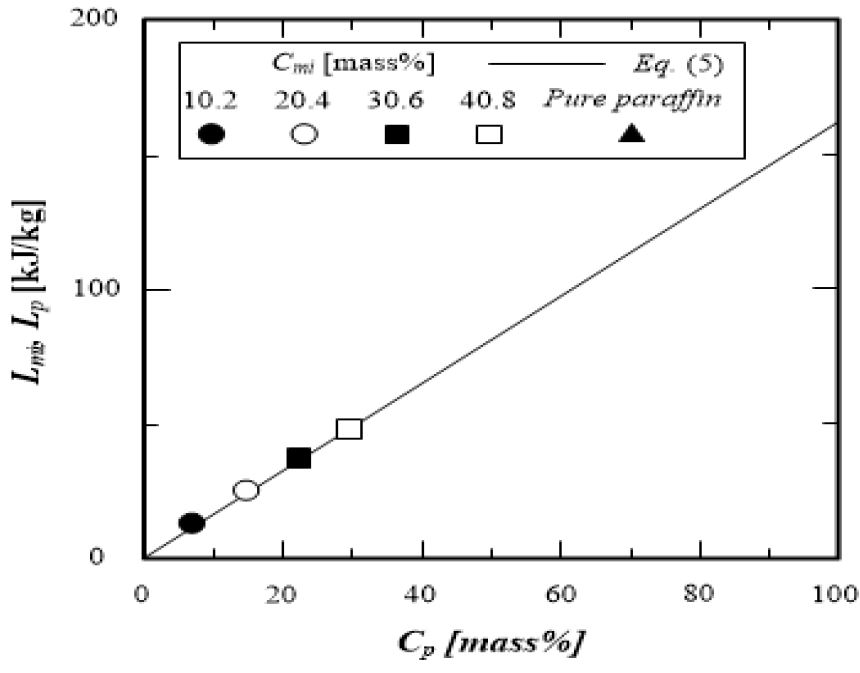
The values calculated by equation (3) are shown in Figure 3 as dashed lines. These calculated values agree with the meas-ured values with an accuracy within ±4.0%; thus, the additive property law is applicable to the estimation of the specific heat of the microcapsule water slurry. Figure 4 shows the measured values of the latent heat of the microcapsule water slurry and the calculated values from equation (4), which are expressed by the mass weight ratio of paraffin to the micro-capsule water slurry and the latent heat of paraffin. The meas-ured latent heat of the microcapsule water slurry is consistent with the calculated value L_mi from equation (4) with an accu-racy within ±3%. It is clarified that the latent heat of the mi-crocapsule water slurry is proportional to the mass weight ra-tio of paraffin to the microcapsule water slurry. The measured melting point T_m of paraffin, which is the dispersion material, coincides with the proposed value [9] with an accuracy within 土2% considering the standard deviation.

Figure 4:

Relationship between latent heat and concentration of paraffin

L m i = C p 100 × L p

(4)

4. Estimation of Density

A specific-gravity meter method was used for measuring the density of the microcapsule water slurry. The specific-gravity meter was mounted in a cylinder, which is filled with the microcapsule water slurry. Supercooling of paraffin, which is the dispersed phase material, is prevented by stirring. The data below the freezing point of paraffin were obtained after stirring the microcapsule water slurry in order to prevent the super-cooling of paraffin.

4.1 Measuring Device and Procedures For Density Measurement

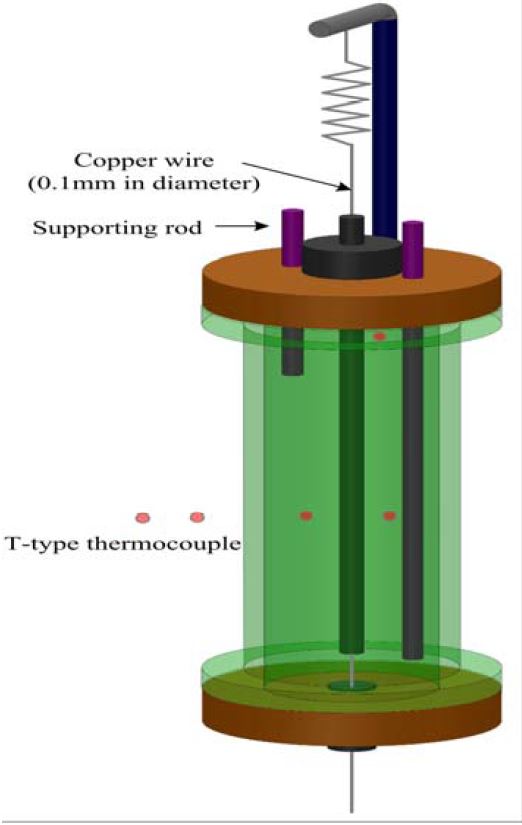
Figure 5 shows the experimental apparatus for the microcapsule water slurry measurements. The temperature of the microcapsule water slurry was controlled by the temperature control bath (temperature range of T = 253–373K, temperature control accuracy ±0.1K). The test microcapsule water slurry (170cm³) was filled into an acrylic cylinder (inner diameter D_I = 30 mm, height H = 300 mm), which was mounted in the temperature control bath. The temperature of the microcapsule water slurry was measured by T-type thermocouples (0.1 mm in diameter), which were located in the acrylic cylinder. The density of the microcapsule water slurry was measured at a constant temperature. The test microcapsule water slurry was mixed with the stirrer at a temperature range below the freezing point (T_m = 278.9K) in order to solidify the dispersed paraffin, which is the phase-change material, without supercooling. The measurement range of the specific-gravity meter was ρ = 700–1000 [kg/m³], and the division of its scale was l [kg/m³]. The accuracy of the specific-gravity meter is within ±0.5%.

Figure 5:

Schematic diagram for the density measurement by Specific-gravity meter

4.2 Measuring Results and Discussion of Density

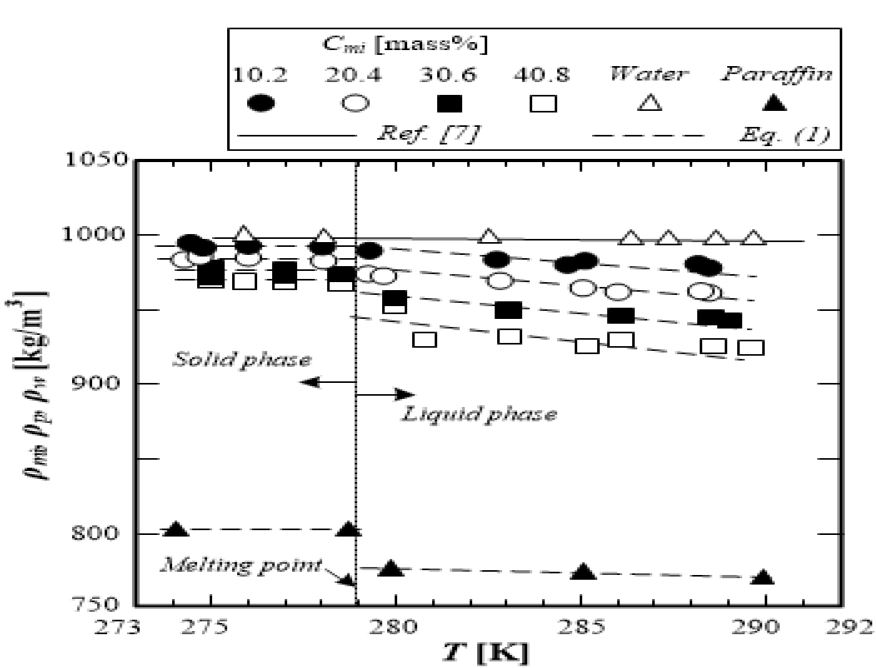
The variations of the densities of the microcapsule water slurry ρ_mi, paraffin ρ_p and water ρ_w with temperature T are shown in Figure 3. The density of paraffin (purity 99.99%) is almost constant (ρ_pl=770kg/m³) in the liquid phase. The density of paraffin in the solid phase is greater (ρ_ps=810kg/m³) than that in the liquid phase.

The dashed line shown in Figure 3 indicates the calculated values of the microcapsule water slurry density by the additional properties law, which is defined by the density and constituent of the wall material, water, and paraffin as follows:

The water density ρ_w(from the published water-steam table) [7] and paraffin density ρ_p(measured in the present study) are used for equation (5). The density of the wall material is constant ρ_me = 1490 kg//m³ from the reference[9]. The calculated values of the microcapsule water slurry density from equation (5) are almost equal to the measured values with an accuracy within ±1.0% (application temperature range is T = 273.0–293.0K). It is understood that the additional properties law equation can be applied to the estimation of the microcapsule water slurry density in both the liquid and solid phases of paraffin as the dispersed phase-change material.

ρ m i = ρ m e × C m e + ρ w × C w + ρ p × C p 100

(5)

Figure 6:

Relationship between density and temperature

5. Estimation of Thermal Conductivity

A transient hot-wire method, using an electrically insulated platinum wire [5][6] was used for measuring the thermal conductivity of the microcapsule water slurry. The transient hot-wire method was used because of the following reasons: (1) the test emulsion is an electrolyte, (2) the transient hot-wire method enables us to measure the thermal conductivity of the microcapsule water slurry even if the paraffin changes phase (solid and liquid phase), and (3) the transient method can be used to measure the thermal conductivity in the required temperature range without natural convection induced from the temperature increase of the hot wire.

5.1 Measuring Device and Procedures For Thermal Conductivity Measurements

The device consisted of an acrylic cylinder (inner diameter D_i = 42 mm, height H = 140 mm, 3.5 mm in thickness) and a platinum wire was used as the hot wire (purity 99.99%, wire diameter 76 μm, length l = 100 mm), which was located in the center of the acrylic resin cylinder. The platinum wire was coated with Teflon (17 μm in thickness) in order to eliminate any electric current leakage to the test sample. Both ends of the platinum wire were supported by enameled copper wires (0.1 mm in diameter). The thermal expansion of the platinum wire was absorbed by the tension of the spring, which is mounted on top of the acrylic resin cylinder. The soldered joint between the platinum and copper wires was electrically insulated using acrylic paint. The relationship between the electric resistance of the platinum wire and temperature was calibrated by a standard thermometer and a precision electric-resistance measuring instrument, in the temperature range of T = 273–313K. The temperature increase of the hot wire was controlled within ∆T = 1.0K. The temperature difference between the top and bottom surface of the test sample in the wire direction was measured by the T-type thermocouples, and the temperature difference was controlled within 0.1K. The thermocouples were calibrated by a standard thermometer; thus, the accuracy of the thermocouples was ±0.05K.

The measurement was initiated by impressing an electric voltage to the hot wire after the temperature of the test sample layer reached a given temperature, which was controlled by a temperature control bath. The thermal conductivity was calculated from equation (6)[4][5] by using the temperature increase ∆T and the elapsed times t₁,t₂.

Figure 7:

Cut view of measuring device of thermal conductivity

λ = q × ln ⁡ t 2 / t 1 4 π ∆ T

(6)

The total accuracy of the device was estimated to be ±2.5%, by considering factors such as the effect of Teflon coating on the temperature rise of the hot wire, the measuring accuracy of the electric voltage, and the measuring accuracy of the wire length. An experimental check of the device’s accuracy was carried out by using pure water. The results coincide with the reference values [8] with an accuracy within ±2.5%.

Eucken’s dispersion model [10] was then applied to estimate the thermal conductivity of the test microcapsule water slurry.

5.2 Measuring Results and Discussion of Thermal Conductivity

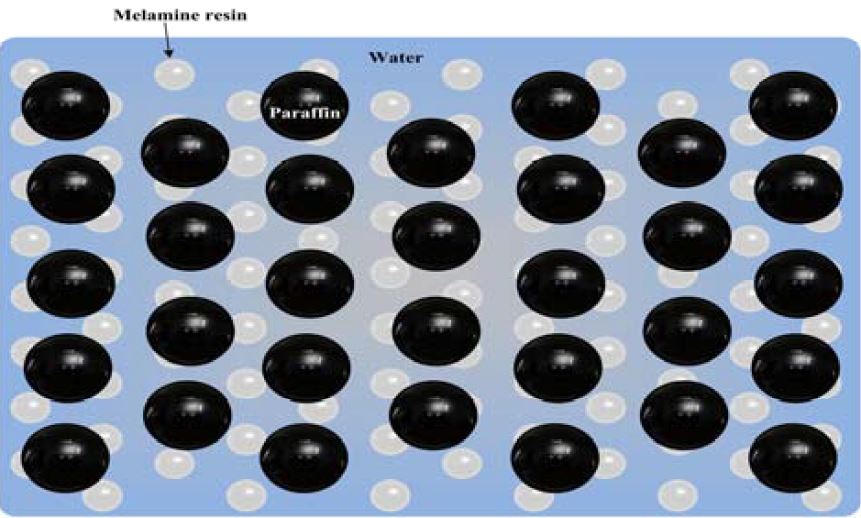
The surfactant forms melamine in the water solution, and it makes a wall around the dispersed paraffin in the microcapsule water slurry. At the beginning, the thermal conductivity of the spherical surfactant construction is complex in the test microcapsule water slurry. The thermal conductivity of the microcapsule water slurry was estimated using the measured results of the two phases (melamine and water). An estimation of the thermal conductivity of the microcapsule water slurry is very difficult because the paraffin (phase-change material) is dispersed in water and coated with the wall material. In this study, the spherical paraffin dispersed in water was assumed for the thermal conductivity model of the microcapsule water slurry, as shown in Figure 8. The thermal conductivity of the assumed microcapsule water slurry model (Eucken’s model) was calculated using the thermal conductivity of water, paraffin, and the microcapsule water slurry as follows:

Figure 8:

Eucken’s dispersion model

λ m i = λ w 1 - 2 ϕ λ w - λ p 2 λ w + λ p + ψ - ϕ λ w - λ m e 2 λ w + λ m e 1 + ϕ λ w - λ p 2 λ w + λ p + ψ - ϕ λ w - λ m e 2 λ w + λ m e

(7)

where the thermal conductivity of paraffin is calculated from equation (8). The calculated values in the solid phases are shown in Figure 9 as dashed lines.

λ p = - 9.03 × 10 - 6 T 2 - 2.2 × 10 - 3 T + 1.65 273 K ≺ T ≺ 278.9 K

(8)

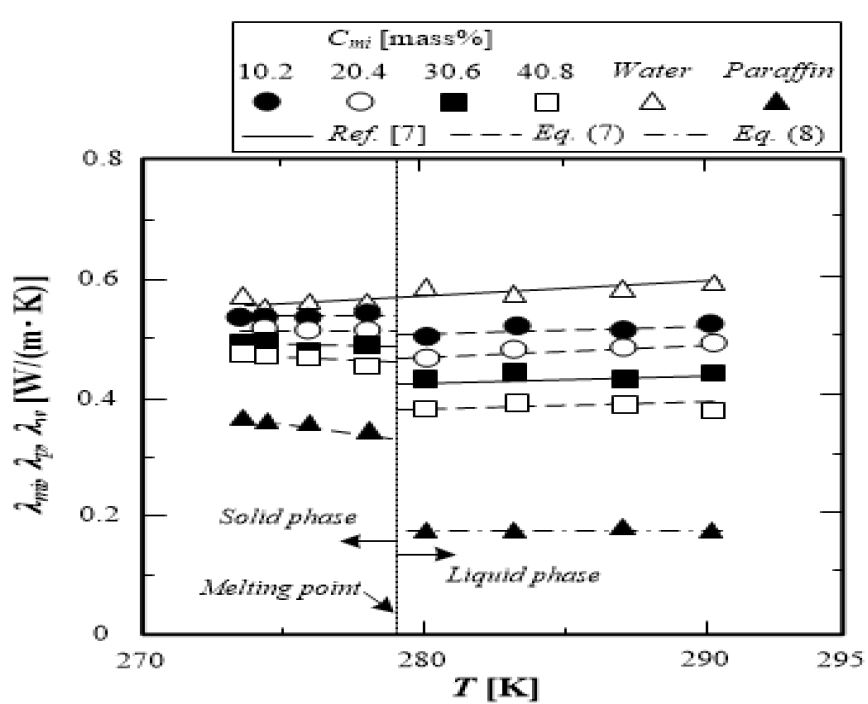
Figure 9 presents the variations of the thermal conductivity of the test microcapsule water slurry λ_mi, water λ_w, and paraffin λ_p with temperature T. The dashed lines indicate the calculated values from equation (7). The thermal conductivity of paraffin is plotted in Figure 8 as the plus. The thermal conductivity of paraffin decreases with an increase in temperature in the solid phase. In contrast, the thermal conductivity of paraffin in the liquid phase is almost constant. The thermal conductivity of water is greater than that of paraffin, and it increases slightly with temperature.

The thermal conductivity of the microcapsule water slurry shows a different behavior below and above the freezing point. The thermal conductivity of the microcapsule water slurry decreases with increasing paraffin concentration. The thermal conductivity of the microcapsule water slurry for a low paraffin concentration is dependent on the thermal conductivity of water. The temperature dependence of the thermal conductivity of the microcapsule water slurry shows a decreasing tendency with an increase in the paraffin concentration. The calculated values from equation (7) are consistent with the measured results with an accuracy within 土0.9%. Therefore, Eucken’s dispersion model can be applied to the estimation of the thermal conductivity of the microcapsule water slurry.

Figure 9:

Relationship between thermal conductivity and temperature

6. Conclusion

The thermal properties of a microcapsule water slurry were measured, which included the dispersed phase-change (latent heat-storage) material. The following conclusions were obtained.

(1) The density of the microcapsule water slurry was measured using a specific-gravity meter. It was determined that an appropriate property law could be applied to estimate the microcapsule water slurry density with paraffin (dispersed phase), water (continuum phase), and melamine density.

(2) The specific heat of the microcapsule water slurry was measured by a water-calorimeter. The specific heat of the microcapsule water slurry could also be estimated using the property law mentioned above.

(3) A transient hot-wire method was used for the measurement of the thermal conductivity of the microcapsule water slurry in the solid and liquid phases of the dispersion material. It was clarified that a modified Eucken model could be applied to the estimation of the thermal conductivity of the microcapsule water slurry.

Acknowledgments

This microcapsule was provided by KIER (Korea Institute of Energy Research).

References

H. Inaba, and S. I. Morita, “Fundamental study of cold heat storage system of O/W-type emulsion having cold latent heat dispersion material (2nd Report, Flow and cold heat-storage characteristics of emulsion in a coiled double-tube heat exchanger)”, JSME International Journal Series B: Fluids and Thermal Engineering, 60(572), p1422-1429, (1994). [https://doi.org/10.1299/kikaib.60.1422]
H. Inaba, “Ice heat-storage system and multiphase flow (Multiphase Flow Lecture Series 9)”, Japanese Society for Multiphase Flow, 97, (1992), (in Japanese).
M. Yoshida, “High-efficiency heat-transport fluid containing microencapsulated phase-change material (1) flow characteristics”, Kagakukougaku Symposium Series 23, p32, (in Japanese).
Y. Nagasaka, and A. Nagashima, “Precise measurement of the thermal conductivity of liquids: 2^nd Report, An absolute meassurement of the thermal conductivity of electrically conducting liquids by the transient hot-wire method”, The Japan Society of Mechanical Engineers, 47(419B), p1323-1331, (1981), (in Japanese).
H. Inaba, H. Otake, S. Nozu, and T. Fukuda, “A study on latent heat storage using a supercooling condition of hydrate: 1^st Report, An entimation of properties of hydrate sodium acetate including a supercooling condition”, The Japan Society of Mechanical Engineers, 58(553B), p2848-2856, (1992), (in Japanese). [https://doi.org/10.1299/kikaib.58.2848]
Chemical Handbook Editorial Department, Chemical Handbook, Ohm, p232, (1987), (in Japanese).
Japan Society of Mechanical Engineers, “JSME Data Book: Heat Transfer 4th Ed.”, Japan Society of Mechanical Engineers, 331, (1986), (in Japanese).
H. Inaba, K. Takeya, and S. Nozu, “Effect of various parameters on a supercooling phenomenon of still bulk water and water solution”, The Japan Society of Mechanical Engineers, 59(560B), p1202-1209, (1993), (in Japanese). [https://doi.org/10.1299/kikaib.59.1202]
Japan Society of Thermophysical Properties, “Thermophysical Properties Handbook”, Yokendo, p120, (1990), (in Japanese).
T. Saito, and O. Okagaki, “Thermal conduction in wet materials”, The Japan Society of Mechanical Engineers, 62(484), p741-747, (1959), (in Japanese).