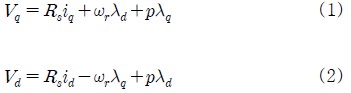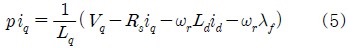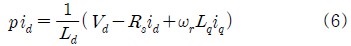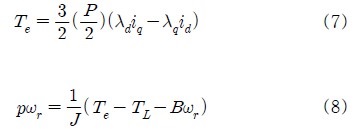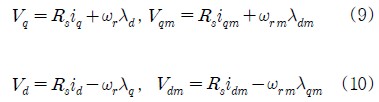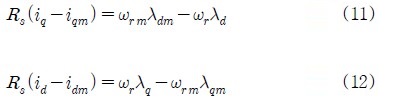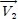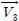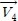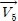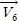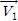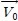A new sensorless speed control method for permanent magnet synchronous motor using direct torque control

1. 서 론

영구자석 동기전동기는 효율이 높고 고출력이 가능하여 산업 전반에 많이 사용되고 있다[1]. 영구자석 동기전동기의 구동을 위해 현재는 벡터제어가 많이 사용되지만 이의 구현을 위해서는 위치 및 속도센서를 사용해야 하며 복잡한 연산 및 제어기를 사용하게 되므로 시스템 구현이 용이하지 않게 된다[2]. 이러한 단점을 극복하기 위해 직접토크제어가 고안되었는데 이것은 원래 유도전동기를 제어할 목적으로 개발된 속도 제어법이다[3].

직접토크제어는 토크, 자속 지령치와 전동기의 발생 토크 및 자속 값을 허용된 히스테리시스 폭 범위 안에서 서로 비교하여 최적의 공간전압 벡터를 얻기 위해 인버터 스위칭 테이블을 사용한다[4]. 그리고 이 제어방식은 복잡한 연산 없이 제어시스템을 구현할 수 있고 전동기 파라미터 변화에 강인한 제어특성을 가진다[5].

본 논문은 전류오차보상법[6]과 직접토크제어를 이용하여 간단하고 강인하며 제어시스템 구현이 용이한 영구자석 동기전동기의 새로운 센서리스 속도제어 방법을 제안하며 컴퓨터 모의실험을 통해 제안한 방식의 유효성을 입증하려고 한다.

2. 직접토크제어

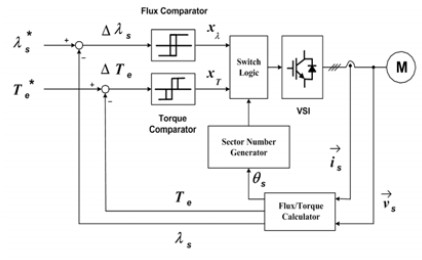
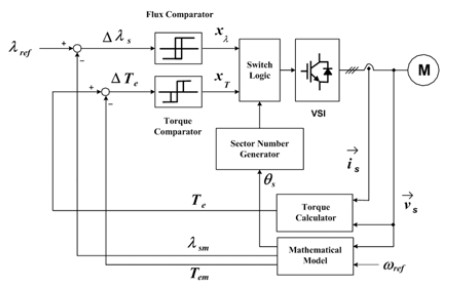
Figure 1은 직접토크제어의 블록선도를 보여준다. Figure 1에서 자속 및 토크 비교기(Comparator)는 둘 다 히스테리시스 형식이며, 자속 비교기는 2가지(x_λ=+1,-1) 출력을 내보내고 토크 비교기는 3가지x_T(=+1,0,-1) 경우를 출력시킨다. 여기서 '+1'은 고정자 자속이나 토크 각의 증가를 의미하고 '-1'은 자속이나 토크 각의 감소를 나타내며 '0'은 토크 변화를 요구하지 않음을 의미한다.

Figure 1:

Scheme of direct torque control

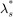Figure 1에서 는 자속 지령치, 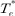는 토크 지령치이다. Δλ_s는 자속 지령치와 전동기 자속의 비교값이고 ΔT_e는 토크 지령치와 전동기 발생 토크를 상호 비교한 값이다. 그리고 θ_s는 고정자 좌표의 d축을 기준으로 표시한 고정자 자속벡터의 각이다.

Table 1:

Switching logic (counterclockwise direction)

Table 1은 반시계 방향으로 회전하는 고정자 기준 자속을 발생시키기 위한 스위칭 논리를 나타낸다. 입력 변수는 x_λ, x_T및 영역(Ⅰ~ Ⅵ)이며 출력 변수는 인버터 전압벡터가 된다.

Figure 2:

Principle of direct torque control

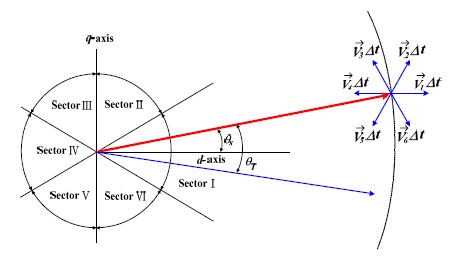
Figure 2는 직접토크제어의 개략적인 원리를 설명해준다. 각 스위칭 영역에서 자속 및 토크 조건에 따라 Table 1을 이용하여 최적의 전압벡터가 선정된다. Figure 2에서 θ_T는 고정자 및 회전자 자속벡터 사이의 토크 각이다

3. 센서리스 속도제어

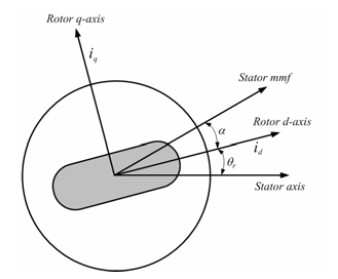
Figure 3은 영구자석 동기전동기의 모델을 나타낸다. 회전하는 회전자 d축은 고정된 고정자 축과 θ_r의 각도를 가지며 회전하는 고정자 자속은 회전자 d축과 α의 각도를 만들며 회전자와 동일한 속도로 회전한다.

Figure 3:

Model of PMSM

회전자 기준좌표를 사용한 영구자석 동기전동기의 고정자 전압방정식은 다음과 같다.

식 (1), (2)에서 V_q, V_d는 고정자전압, R_s는 고정자저항, i_q, V_d는 고정자전류, ω_r은 회전자 속도, λ_d, λ_q는 고정자자속 및 p는 미분연산자이다.

전동기의 쇄교 자속은 다음과 같다.

식 (3), (4)에서 L_q, L_d는 자기인덕턴스, λ_f는 영구자석의 쇄교 자속이다.

식 (3), (4)를 식 (1), (2)에 대입하고 전류에 관한 방정식으로 정리하면 다음과 같은 식을 얻을 수 있다.

그리고 전동기의 발생토크 및 회전자속도는 다음 식으로 표현된다.

식 (7), (8)에서 T_e는 발생토크, P는 극수, J는 관성모멘트, T_L은 부하토크, B는 제동계수이다

식 (5), (6), (7), (8)에 의해 영구자석 동기전동기는 고정자전압을 입력받아 고정자전류 및 회전자속도를 출력하는 시스템으로 생각할 수 있다. 이것을 그림으로 나타내면 Figure 4와 같다.

Figure 4:

Input and output variables of PMSM

식 (5), (6)을 이용하여 Figure 4의 전동기와 전기적 파라미터가 동일한 수식모델을 고려하면 Figure 5와 같이 표현할 수 있다.

Figure 5:

Input and output variables of model

Figure 5에서 수식모델의 입력전압은 실제 전동기의 고정자전압과 같고 입력 회전자속도는 속도 설정값을 사용하며 고정자전류를 출력한다. Figure 5에서 첨자 m은 수식모델 변수를 나타내고 ω_ref는 수식모델의 속도로서 속도 설정값이다. 식 (5), (6) 은 기계적 파라미터를 포함하지 않으므로 이들에 대한 정보는 필요 없게 된다.

Figure 4, 5에서 수식모델이 실제 전동기를 정확하게 표현할 경우, 실제 전동기의 전압, 전류가 수식모델과 일치할 때에는 전동기의 회전자 속도도 설정치인 수식모델의 회전자 속도와 같게 될 것이다. 식 (1), (2)를 이용하여 과도상태를 무시한 전동기 및 수식모델의 전압방정식을 표현하면 다음과 같다.

식 (9), (10)에서 전동기와 수식모델에 같은 고정자전압을 인가하면 다음과 같은 식이 얻어진다.

따라서 수식모델과 전동기 고정자 전류 사이의 전류오차를 보상하면서 양자에 동일한 전압을 인가한다면 식 (11), (12)에 의해 전동기 회전자 각속도인 ω_r이 설정치인 수식모델의 회전자 각속도 ω_rm과 같아지게 된다.

본 논문에서는 수식모델과 전동기의 전류를 일치시키는 방법으로 직접토크제어를 사용하였다. 전동기 전압과 전류값을 이용하여 고정자자속 크기와 위상각을 계산하고 수식모델과 전동기의 발생토크를 계산하여 일치하도록 하면 양자의 고정자 전류값이 동일하게 되며 전동기의 회전자속도는 설정값에 접근하게 된다.

예를 들어 설정치인 수식모델의 속도가 실제 전동기 속도보다 높은 경우 전동기의 토크가 수식모델의 토크보다 크게 된다. 이 경우 직접토크제어에 의해 양자에 공급되는 동일한 전기자 전압을 상승시키면 전동기 속도는 증가하여 모델의 속도에 접근하게 되고, 결국 양자의 토크차이도 감소하게 된다. 앞의 상황과 반대인 경우는 전기자 전압을 감소시켜 동일한 효과를 기대할 수 있다.

Figure 6은 본 논문에서 제안한 영구자석 동기전동기의 센서리스 속도제어 블록선도이다.

Figure 6:

The proposed control method

Figure 6에서 전동기에 인가되는 전압 및 전류를 측정하여 전동기 발생토크를 계산하고 전동기에 인가되는 전압을 수식모델에 똑같이 인가하여 수식모델의 발생토크 및 자속을 계산한다. 그리고 자속 지령치 λ_ref와 수식모델의 자속을 서로 비교하고 전동기 발생토크도 수식모델 발생토크와 서로 비교한 후 각각의 비교기를 거쳐 스위칭 테이블에 의해 인버터 전압이 발생하도록 구성되어 있다.

본 논문에서 제안한 방식은 직접토크제어를 사용하므로 좌표축 변환이 없어 쉽게 구현이 가능하고 PI제어기도 사용하지 않고 센서리스 속도제어를 수행하는 독특한 구조를 가진다.

4. 컴퓨터 모의실험

본 논문의 제어방식 유효성 입증을 위해 컴퓨터 모의실험을 수행하였다.

수치해석 소프트웨어인 MATLAB을 사용하여 모의실험을 수행하였으며 모의실험에 사용된 영구자석 동기전동기 파라미터는 Table 2와 같다.

모의실험에서는 저속영역, 고속영역의 계단상 속도지령에 추종하는 속도 응답특성 및 고속영역에서의 반전속도 응답특성을 확인하려고 한다. 그리고 마지막으로 중속영역에서의 부하특성도 고찰하려고 한다.

Table 2:

Parameters of motor

Figure 7:

Speed step change(0→100[rpm])

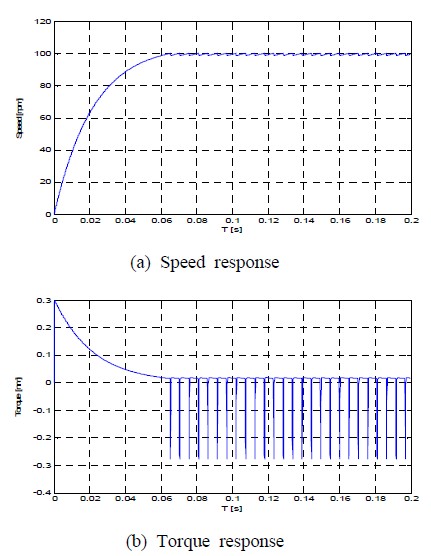
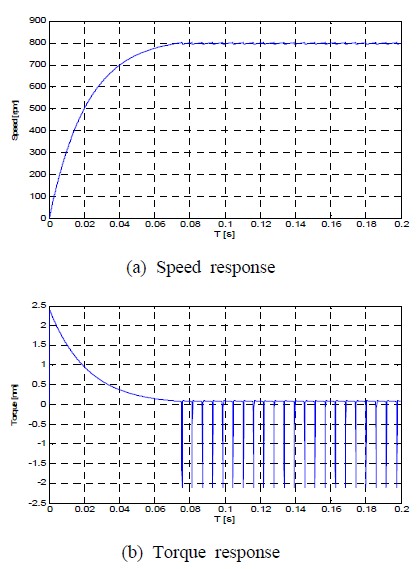
Figure 7은 0[rpm]에서 100[rpm]으로, Figure 8은 0[rpm]에서 800[rpm]으로 각각 계단입력 속도지령을 가했을 경우 전동기의 속도 및 토크 응답특성을 나타낸다. 저속영역 및 고속영역에서 센서리스 속도 응답특성이 양호함을 알 수 있다.

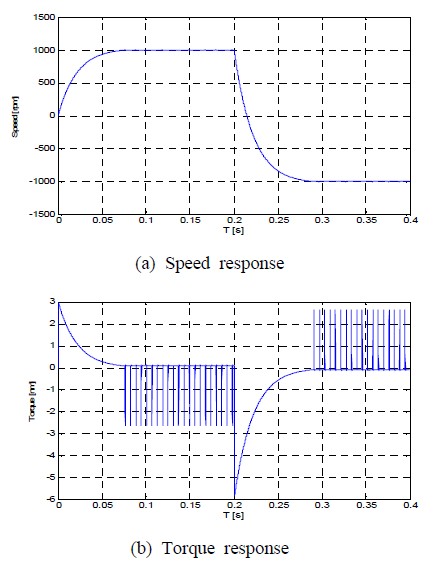
Figure 9는 1000[rpm]의 속도지령을 인가하고 0.2초 후 -1000[rpm]의 반전속도지령을 인가했을 경우의 속도 및 토크 응답특성을 나타낸다. 그림에서 알 수 있듯이 고속영역에서 반전속도 특성이 우수함을 알 수 있다.

Figure 8:

Speed step change(0→800[rpm])

Figure 9:

Speed change(1000→-1000[rpm])

Figure 10:

Change of load torque(0→0.1[N·m])

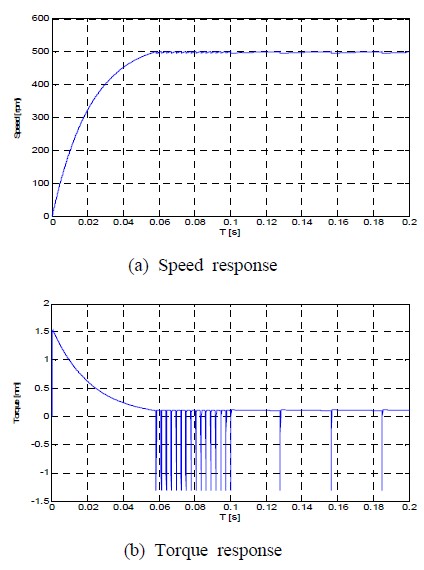
Figure 10은 0[rpm]에서 500[rpm]으로 계단 속도지령을 인가하고 0.1초 후 0.1[N·m]의 부하토크를 인가하였을 경우의 속도 및 토크응답을 나타낸다. 중속영역에서 부하특성이 양호함을 알 수 있다.

컴퓨터 모의실험 결과 본 논문에서 제안한 방식의 저속 및 고속 운전특성, 전동기 속도 반전특성 및 중속에서의 부하특성이 양호함을 확인하였다.

5. 결 론

본 연구에서는 영구자석 동기전동기의 센서리스 속도제어를 위해 수식모델의 전류와 전동기 전류 사이의 오차를 보상하는 전류오차보상법을 사용하였으며 전동기 구동을 위해 직접토크제어를 이용하였다.

제어시스템에서 센서를 사용하지 않기 때문에 보다 신뢰성 높은 제어시스템을 구성할 수 있고 직접토크제어를 사용함으로써 파라미터 변화에 강인하며 복잡한 연산 없이 단순하게 제어시스템을 설계할 수 있다.

제어시스템의 유효성 확인을 위해 컴퓨터 모의실험을 수행하였으며 저속, 고속영역의 속도지령에 대한 응답특성, 고속영역에서의 속도 반전특성 및 중속영역에서의 부하특성을 확인하였다.

그리고 차후 실제 실험을 통하여 본 논문에서 제안한 방식의 우수성을 검증하려고 한다.

References

• J. x. Xu, S. K. Panda, Y. J. Pan, T. H. Lee, and B. H. Lam, “A modular control scheme for PMSM speed control with pulsating torque minimization”, IEEE transactions on industrial electronics, 51(3), p526-530, (2004). [https://doi.org/10.1109/TIE.2004.825365]
• C. Mademlis, and N. Margaris, “Loss minimization in vector controlled interior permanent magnet synchronous motor drives”, Industrial Electronics, IEEE Transactions on, 49(6), p1344-1347, (2002). [https://doi.org/10.1109/TIE.2002.804990]
• T. G. Habetler, F. Profumo, M. Pastorelli, and L. M. Tolbert, “Direct torque control of induction machines using space vector modulation”, IEEE Transactions Industrial Application, 28(5), p1045-1053, (1992). [https://doi.org/10.1109/28.158828]
• C. Lascu, I. Boldea, and F. Blabjerg, “A modified direct torque control for induction motor sensorless drive”, IEEE Transactions On industrial Application, 36(1), p22-30, (2000). [https://doi.org/10.1109/28.821806]
• M. Pacas, and J. Weber, “Predictive direct torque control for the PM synchronous machine”, IEEE transactions on industrial electronics, 52(5), p1350-1356, (2005). [https://doi.org/10.1109/TIE.2005.855662]
• Sae Gin Oh, Jong Su Kim, and Sung Hwan Kim, “Sensorless Speed Control of Induction Motor using Current Compensation”, Journal of the Korean Society of Marine Engineering, 27(4), p503-510, (2003).