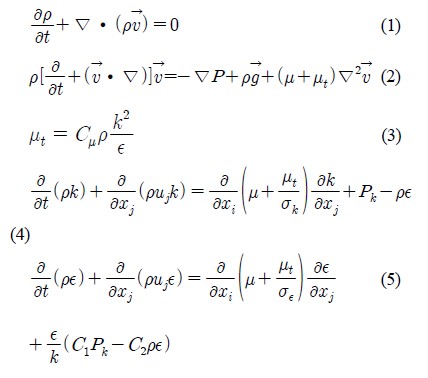The effect of eccentricity between gear and housing in involute gear pump
The characteristics of involute gear pump with eccentric gap between gear tip and housing have been studied in terms of volumetric flow rate and/or flow efficiency. The analysis has been done with FLUENT/R-13 employing with k-e model for the turbulent flow under the given conditions of rotational velocity, gap distance and outlet pressure. The effect of parameters continues to be shown for the eccentric gear as same as for the concentric gear such that the volumetric flow rate (volumetric efficiency) increases as the increases of rotational velocity and decrease of gap distance and of outlet pressure. In the meantime, the shape of pressure build-up appears to be exponentially increase as gap distance decreases at upstream position. The pressure is rapidly developing in the upstream and remains almost constant thereafter in the downstream of circumferential flow path. This typical characteristics becomes more profound as eccentricity increases. The pump performance for the eccentric gear pump with minimum gap distance shows better than its concentric counterpart. However, it shows not for the concentric pump with minimum gap distance. Therefore, the gap reduction due to eccentricity may be positive for pump performance.
초록
기어 끝단과 하우징 사이의 간극이 회전방향으로 편심된 인벌류트펌프에서 체적유량과 유량효율을 검토하였다. 해석은 k-e 모델을 이용하여 FLUENT/R-13을 사용하여 기어의 회전속도, 간극의 거리 및 출구압력이 주어져 있을 경우 난류유동을 해석하였다. 동심축과 편심축의 경우 체적유량을 비롯한 유동특성에 대해 독립변수들의 영향은 지속되었으나 회전방향에 대한 압력 분포는 서로 달라 편심의 경우 상류부에서 대부분의 압력이 상승하고 하류부의 압력은 거의 일정한 특성을 보였으며 편심의 영향이 클수록 이러한 현상은 심하게 나타났다. 편심펌프에서 유동특성은 최소 간극에 의존하며 체적유량 혹은 체적효율은 편심되기 전 동심축보다 크나 최소간극과 같은 크기의 동심펌프보다는 작다. 펌프에서 기어축의 편심에 의한 간극 축소는 펌프성능에 긍정적인 영향을 미칠 수 있다.
Keywords:
Involute gear pump, Dynamic mesh, k-e model, Flow rate, Eccentric gear, 인벌류트 기어펌프, 동적메쉬, 난류모델, 유량, 편심기어1. 서 론
최근 토목, 건설장비 및 고압용 기계에 사용되는 기어펌프는 구조가 간단하고 가격이 저렴하며 작동유의 오염, 유온상승, 과부하 등의 가혹한 사용조건에서도 다른 종류의 펌프에 비해 신뢰성이 크기 때문에 건설 기계 및 중장비, 농업기계 등의 산업의 각 분야에서 널리 사용되고 있다. 날로 증가하는 소비자의 고품질 요구를 만족시키며, 성능향상과 원가절감이라는 과제를 안고 있어 이에 대응하고자 많은 종류의 부품과 설계방식을 선보이고 있다. 그러나 그 기계들의 유압원인 기어펌프에 대한 체계적인 이론이 명확히 정립되지 않고, 기어펌프에 대한 정보의 대부분이 실험에 의존하고 있는 상황이므로 정확한 유체역학적 메커니즘의 이해가 부족한 실정이다. 또한 기어펌프에 대한 해석이 이루어지더라도, 실제적인 상황인 기어가 편심이 된 상황이 아닌, 기어 끝단과 하우징 사이의 간극이 일정한 이상적인 상황(동심축)에 대한 해석이 이루어져 왔다[1]-[7]. 그러나 거의 모든 작동 조건에 따르면 출구의 압력이 입구의 압력에 비해 매우 크므로 기어의 축은 하부로 쳐지게 되어 기어 축과 하우징 사이의 간극이 차이가 발생하여 각 회전축은 편심이 이루어지게 된다. 따라서 본 연구는 동심축에 대한 결과[1]에 이어 실제 오일펌프에서 발생하는 편심에 의한 압력과 유동의 특성이 어떻게 변하는지에 대한 분석을 통해 오일펌프의 설계 및 제작에 고려해야할 문제점을 파악하고자 한다. 본 연구는 유동해석 상용프로그램인 Fluent를 이용하여 기어 끝단과 하우징 사이의 간극(편심량), 기어회전수, 기어펌프 입구와 출구의 압력차이 등에 따른 기어펌프 내부의 압력특성과 유동특성을 제시하고 이의 결과를 분석하고자 한다.
2. 이론 및 수치해석
2.1 이론
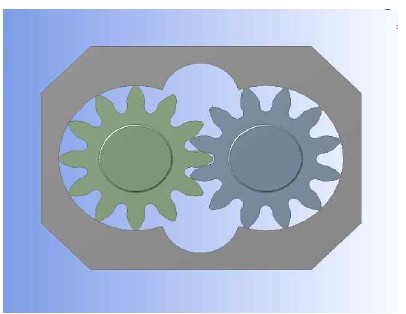
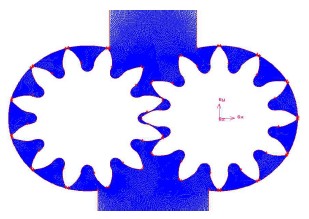
Figure 1은 대표적인 인벌류트 기어를 이용한 외접형 기어펌프의 형태로, 기어와 하우징으로 구성되어 있다. 기어펌프의 하부는 기어펌프의 입구로서 대기압이 형성되어 있고 상부는 출구로서 일정한 고압이 형성되어 있다. 인벌류트 기어펌프는 구동축기어(오른쪽)와 종동축기어(왼쪽)가 서로 맞물려 돌면서 하부의 오일을 상부로 이동시키는 구동 형태를 가지며, 구동축이 반시계방향으로 움직인다. 또한 인벌류트 기어의 잇수는 한 기어당 12개씩이며, 총 24개를 갖는다. 본 연구에서는 기본적인 유체역학적 메커니즘과 해석의 용이성을 위해 기어펌프 중심에서 절단하여 2차원으로 해석을 수행하였다.
기어펌프의 유동해석을 위한 시스템의 지배방정식은 연속방정식과 운동량방정식으로 식(1)과 식(2)와 같다. 또한 난류의 유동해석은 표준 k -
 모 델을 이용하였다. 난류점성계수는 난류운동에너지(k)와 난류소산에너지(
모 델을 이용하였다. 난류점성계수는 난류운동에너지(k)와 난류소산에너지(
 )의 난류 수송 방정식으로 구할 수 있다. 난류수송방정식은 식 (4), (5)에 나타내었다.
)의 난류 수송 방정식으로 구할 수 있다. 난류수송방정식은 식 (4), (5)에 나타내었다.
식(5)에 제시된 상수는 C1 = 1.44 , C2 = 1.92 , Cμ = 0.09을 사용하였고 Pk는 난류생성을 나타낸다. 자세한 내용은 참고문헌[8]에 나타나 있다.
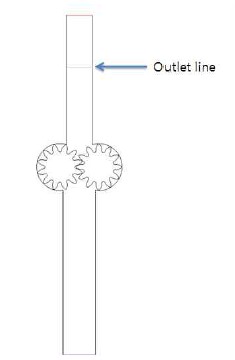
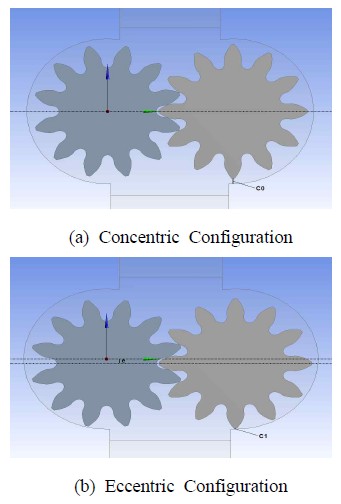
Figure 2는 본 연구에서 사용한 기어펌프의 전체 해석영역의 개념도이다. 흡입 및 토출부의 유로는 경계조건으로 부터의 유동간섭을 최소화하기 위하여 각 단면의 5배 길게 하였다. 유동간섭의 영향 및 내부 유동의 결과를 도출하기 위해 토출 부분에 선을 생성하였다. 해석에 이용된 2차원 모델에 대한 치수는 Table 1에 나타내었다. Figure 3은 기어 축의 편심영향을 파악하기 위해 정성적으로 도시한 하우징과 기어의 형상을 제시하였다. 동심 축에서는 기어끝단과 하우징 사이의 간극을 0.05mm 기준으로 고려하였으며 기어 중심축을 하부로 0.01mm씩 아래로 편심 시켜 해석을 수행하였다. 따라서 동심간극 고려한 최소간극은 0.03mm와 0.02mm를 고려하였다. Figure 3(a)는 기어 및 하우징의 동심 축에 의한 배열이며 Figure 3(b)는 축의 편심으로 인해 하부에 최소 간극이 형성되는 배열을 각각 도시하였다.
2.2 수치해석
본 연구에서 사용된 격자시스템을 Figure 4에 나타내었다. 모든 해석의 경우 약 10만개의 삼각격자계를 이용하였으며, 특히 기어의 회전으로 인한 복잡한 유동장의 형성 및 급격한 유동영역의 변화가 예상되어 정확도를 높이기 위해 간극을 포함한 기어 주위에 상대적으로 조밀한 격자를 형성하였으며, 두 기어의 회전에 의해 연속적으로 변하는 계산영역은 기어의 회전과 함께 매 계산시간마다 기어주위의 격자가 자동적으로 재생성(Remeshing)되도록 하는 동적메쉬(Dynamic mesh)기법을 이용하였다.
본 연구에서는 기어펌프 내 유동장을 2차원 비압축성, 점성유동으로 가정하였으며 앞서 언급했듯이 상용 해석프로그램인 Fluent을 사용하였다. 모델의 특성상 기어 끝단과 하우징 사이의 간극, 기어와 기어가 맞물릴 때의 매우 좁은 간극에서는 속도가 상당히 커서 난류유동이 예상되므로 앞서 언급한 난류모델을 사용하였다. 격자수와 유동모델에 따른 결과의 신뢰성을 확보하기 위해 층류해석 및 격자수 15만개를 각각 사용하여 본 연구에서 사용된 난류모델과 10만개의 격자수의 압력분포 및 체적유량과 비교한 결과는 충분한 신뢰성을 갖는다고 판단된다.
본 연구에서 사용한 오일은 SAE 30(밀도 : 912 kg/m3, 점성계수 : 0.38 kg/m∙s)이며 나머지 해석에 사용한 변수는 편심도, 기어의 회전속도 및 입출구의 압력차이를 고려하였으며 사용된 변수의 해석 범위는 Table 2에 나타내었다. 여기서 최소간극이라 함은 처진 기어의 중심축과 하우징 간에 간극이며 이는 동심축(간극 0.05mm)이 처진 것이므로 하류부(기어의 상부)는 간극이 벌어져 0.05mm보다 커짐을 기억하라.
동적격자시스템을 이용한 기어의 움직임을 모의하기 위해 비정상유동으로 해석을 수행하였으며, 기어 끝단과 하우징 사이의 매우 작은 틈새(0.02mm)의 유로해석을 가능하게 하기위해 시간간격은 1 × 10-7초로 설정하여 해석을 수행하였다. Table 2에 주어진 입력조건 혹은 경계조건을 가지고 기어의 움직임에 대한 해를 구하는 기법은 크게 2가지로 알려져 있다. 입구의 체적유량을 입력으로 하여 입출구의 압력 차이를 구하는 방법과 본 연구에서 사용된 바와 같이 입출구의 압력을 일정하게 주고 해의 일부로서 체적유량을 구하는 방법이다. 자세한 수치해석의 기법은 참고문헌[1]에 서술되어 있다. 한편 해석은 난류로 고려하였으므로 난류유동의 결과를 얻기 위해 먼저 층류로 가정하여 입구속도의 크기와 분포를 얻은 후 입구에서 난류강도를 약 3%로 정의하여 난류유동이 수렴할 때까지 재해석을 수행하였다.
본 연구에서 이용한 수렴조건은 연속방정식, 운동량 방정식, k 방정식,
 방정식으로 연구수행에 사용된 미분방정식에 대한 각각의 조건을 만족하여야 한다. 각각의 수렴조건이 연속 계산의 상대오차가 1 × 10-6보다 작아질 때까지 반복계산을 수행하였다.
방정식으로 연구수행에 사용된 미분방정식에 대한 각각의 조건을 만족하여야 한다. 각각의 수렴조건이 연속 계산의 상대오차가 1 × 10-6보다 작아질 때까지 반복계산을 수행하였다.
3. 결과
3.1 압력분포
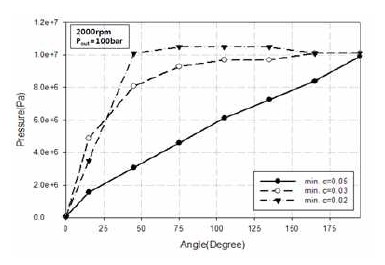
Figure 5는 출구압력 100bar, 기어회전수 2000 rpm인 경우 기어의 원주방향에 따른 압력 변화를 나타낸 것이다. Figure 5(a)와 Figure 5(b)는 각각 편심에 따라 최소간극 0.03mm와 0.02 mm일 때 압력분포를 도시한 것이다. 전체적으로 입구에서 출구까지 압력은 원주방향을 따라 증가하며 편심간극의 경우 압력은 기어 입구에서 급격히 증가하고 원주방향에 따라 증가 폭이 감소한다. 이러한 경향을 정량적으로 비교하기 위해 Figure 6에는 원주방향에 따른 기어 사이의 압력을 정량화하여 비교하였다. 동심간극의 경우[1] 압력은 점진적이며 거의 선형적으로 증가하나 편심에 의해 최소간극이 작아질수록 압력은 기어 상류부에서 급격히 올라 간 후 완만하게 증가하거나 출구압력과 거의 같은 압력을 나타내는 지수함수적 분포를 나타내고 있다. 동심간극과는 달리 편심이 발생하면 원주방향에 따라 선형적인 분포가 아니라 출구의 고압이 원주방향의 기어 모듈 아래쪽으로 내려오는 형상을 나타낸다. 이는 기어 상부는 하우징 하부로 위치한 편심에 따라 기어와 하우징 사이의 간극이 넓어져 기어 모듈과 모듈 사이의 저항이 작아지며 반대로 기어 하부는 편심에 따라 작아진 간극에 따라 모듈사이의 저항이 커져 압력에너지가 크게 증가함을 알 수 있다. 따라서 입출구의 압력이 정해져 있는 경우라도 기어펌프 내부의 압력형성에 영향을 미치는 요인은 기어끝단과 하우징 사이의 최소 간극임을 알 수 있다. 이와 현상은 거의 모든 입력변수의 경우에 나타난다.
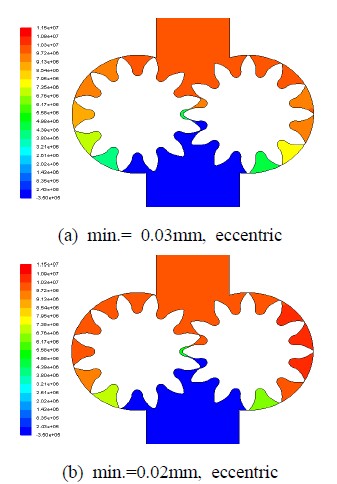
Distributions of pressure for different minimum clearances due to eccentricity(outlet pressure=100bar, 2000rpm)
3.2 속도분포
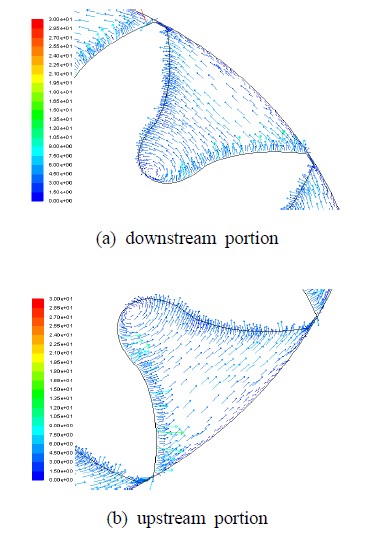
Figure 7에 대표적인 편심간극(min=0.03mm)의 경우 속도분포를 나타내고 있다. 기어사이의 유동영역에서 전체적인 유동특성은 동심간극의 경우와 비슷하며 기어사이의 골부분에 재순환영역과 기어끝단과 하우징 사이에 누유가 발생한다. 편심간극(min=0.03mm)의 경우와 동심간극(0.05mm)을 비교할 때 전반적으로 상류부기어에서 누유가 작고 토출량을 결정하는 기어 움직임과 같은 속도성분이 많은 것으로 보여 전체적인 토출유량의 특성은 상류부에 형성된 최소한의 편심간극에 의존하는 것을 알 수 있다.
3.3 체적유량 및 효율
앞서 압력분포와 속도분포에 대한 정성적인 설명을 체적유량과 효율의 항으로 정량화하기 위해 Figure 8과 Figure 9에 각각 최소간극별 기어회전수에 따른 체적유량과 효율을 도시하였다. 여기서 구한 이론적 체적유량은 기어와 하우징 사이에 간극이 없다고 가정하고 내부 체적을 이용해 구한 값이다. 실선은 상류부 최소간극 0.02mm, 점선은 최소간극 0.03mm, 일점쇄선은 본 연구의 해석의 기준이 되는 동심간극 0.05mm[1]를 의미한다. 그림에서 나타나듯이 편심이 이루어지면 토출유량 또한 증가함을 알 수 있다. 이는 자연적 누유가 발생하는 상류부기어에서 기어끝단과 하우징 사이의 간극이 작아지므로 자연적 누유가 줄어들기 때문이다. 따라서 편심의 양(최소간극이 작을수록)이 클수록 토출유량은 커지며 편심의 양이 다른 경우에도 동심축의 경우와 같이 출구압력과 기어의 회전수의 영향은 계속된다.
Figure 9에는 이론적 체적유량과 해석을 통해 얻어진 체적유량의 비로 효율을 나타내었다. 효율 역시 출구압력이 작고 기어의 회전수가 크며, 최소간극이 작을수록 좋은 것으로 나타났다. Figure 8과 Figure 9의 결과는 간극이 일정한 (0.05mm) 동심축이 처져 상류부에서 최소간극이 0.05mm보다 작아질 경우 체적유량과 체적효율이 커지므로 오히려 바람직한 결과를 얻을 수 있다고 할 수 있다. 그러나 처짐에 의한 최소 간극과 동일한 동심축(0.03mm)의 결과와 비교할 경우에는 Figure 10과 같은 결과를 얻을 수 있다.
Figure 10은 편심축(최소간극= 0.03mm)과 동심축(전체간극= 0.03mm)의 경우에 대해 효율을 검토하였다. 전체적으로 회전수와 출구압력의 영향은 계속되나 최소간극이 같은 경우 편심축의 체적효율은 같은 간극의 동심축의 체적효율보다 오히려 작다. 따라서 인벌류트 펌프의 체적효율에 영향을 미치는 인자는 처짐에 의한 상류부의 최소간극뿐만 아니라 하류부의 간극 또한 영향이 있음을 보여주는 결과이다. 따라서 체적유량 혹은 체적효율은 일반적으로 간극이 작을수록 커지나 이 축이 편심이 될 때 주어진 일정간극보다 최소간극이 작아져 체적유량과 체적효율이 증가한다. 그러나 같은 최소간극을 갖는 동심축 보다는 작다. 효율 증대를 위해 동심축으로 전체간극을 작게 하는 것이 좋으나, 주어진 간극에서 편심축으로 작동시키는 방법 또한 효율을 증대시키는 효과를 나타낼 수도 있다.
4. 결론
본 연구에서는 인벌류트 치형을 가지는 유압식 기어펌프에 대해 출구의 고압으로 인해 형성되는 편심에 대해 해석을 수행하였다. 열유동 해석 상용프로그램인 Fluent를 이용하여 수치해석 모델을 생 성하고 그에 따른 결과를 도출하였다.
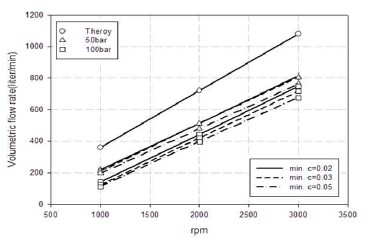
Volumetric flow rate variations in terms of rotational velocity with different outlet pressures and eccentric clearances
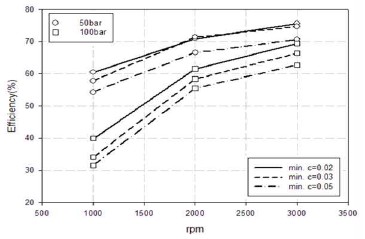
Efficiency variations in terms of rotational velocity with different outlet pressures and eccentric clearances
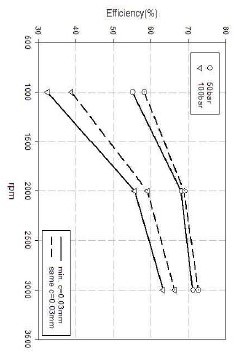
Efficiency variations due to outlet pressures and different center positions for the case of the positive volumetric flow rate
(1) 기존 연구에서 동심 축의 경우 선형적이던 압력분포가 축과 하우징에 편심이 일어남과 동시에 지수함수의(exponential) 형태로 나타났다. 대부분의 압력상승은 최소간극이 유지되는 부분에서 발생하며 편심에 의해 넓어진 하류부분에서는 압력상승이 거의 이루어지지 않음을 의미한다.
(2) 편심 축에서도 동심축의 경우와 유사하게 파라메터 영향(회전수가 클수록, 간극이 작을수록, 출구압력이 작을수록)이 유지되나 주어진 일정 간극을 갖는 축이 편심되어 최소간극이 작을수록 체적유량과 체적효율이 증가한다.
(3) 최소간극과 같은 크기의 동심 축은 같은 크기의 최소간극을 갖는 편심 축에 비해 체적유량 혹은 체적효율이 정량적으로 크다.
References
- S. H. Kim, H. M. Son, and J. C. Lee, “Characteristics of two dimensional flow in an involute gear pump”, Journal of The Korea Fluid Power System Society, 8(2), p36-41, (2011), (in Korean).
-
C. S. Won, N. Hur, and S. H. Kwon, “Flow analysis of automotive oil pump of gerotor type”, Journal of Fluid Machinery, 6(4), p7-13, (2003), (in Korean).
[https://doi.org/10.5293/KFMA.2003.6.4.007]

-
Y.-D. Choi, Y.-T. Kim, and Y.-H. Lee, “CFD analysis of pressure and internal flow for a positive displacement hydraulic turbine”, Journal of the Korean Society of Marine Engineering, 31(6), (2007), (in Korean).
[https://doi.org/10.5916/jkosme.2007.31.6.687]

-
K.-W Nam, S.-H Jo, and J.-I. Park, “Numerical simulation in the IC engine lubricating gerotor oil pump”, Transactions of the Korean Society of Mechanical Engineers B, 30(10), p1019-1025, (2006), (in Korean).
[https://doi.org/10.3795/KSME-B.2006.30.10.1019]

- C.-H. Kim, and J.-Y Jung, “A study on the relief port position of oil hydraulic gear pump with involute teeth”, Journal of the Korean Society of Tribologists and Lubrication Engineers, 16(2), p126-132, (2000), (in Korean).
- Kuo Jao Huang, and Chih Chieh Chen, “Kinematic displacement optimazition of external helical gear pumps”, Chung Hua Journal of Science Engineering, 6(2), p23-28, (2008).
- M. Borghi, M. Milani, F. Paltrinieri, and B. Zardin, “Studying the axial balance of external gear pumps”, Society of Automotive Engineers Technical Paper, (2005).
- Ansys-FLUENT/R-13 User's Guide vol. 2, (2011).