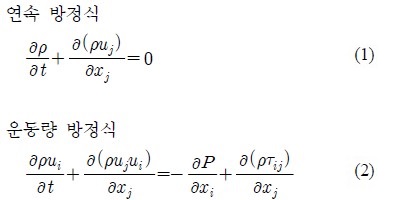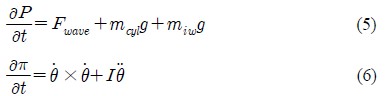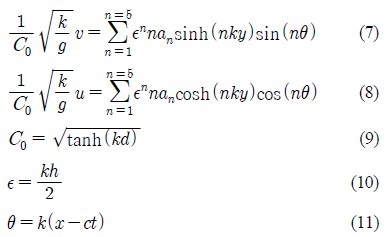Numerical analysis of 2-DOF motions of an ocean floater with sloshing effects

1. 서 론

탱크 내부 유체는 물리적인 외란을 받는 경우, 유체의 자유 표면이 요동하는 현상인 슬로싱이 발생한다. 특히, 해양 부유체는 파랑에 의한 외란이 불규칙적이고, 탱크 내부 슬로싱은 부유체 운동에 직접적으로 영향을 준다. 부유체와 슬로싱의 상호작용을 해석하기 위해 많은 연구가 진행 되고 있으며, 대표적으로 조선 공학 분야에서는 슬로싱에 의한 LNG 선박의 조종력 저감, 탱크 손상, 소음 등의 문제점을 해결하기 위해 슬로싱을 제어하는 연구가 활발하다.

3차원 수치 해석적 접근으로, Kim[1]은 선박운동과 슬로싱 해석을 impulse-response-fuction 법을 이용하여 선박의 자유도 운동을 해석하였고, CFD를 이용하여 유동을 해석하였다. frequency-domain solution과 impulse-response-function법의 진폭응답함수를 비교하였고, Anti-Rolling-Tank의 수위별 슬로싱 감쇠에 대하여 고찰하였다. Lee et al. [2]은 선박 운동에 의한 내부 탱크 슬로싱을 Time domain simulation scheme을 이용하여 해석하였고, 실험과 함께 sway, roll 모션을 중점적으로 분석하였다. S. Mitra et al. [3]은 Novel time domain simulation scheme을 이용하여 비선형 슬로싱과 선박운동을 바람과 해류, 파랑의 효과를 고려하여 탱크내부 슬로싱을 해석하였다. C.H. Wu et al. [4]은 다양한 파랑 방향, 형태에 대한 외란을 이용하였다. 사각 탱크와 슬로싱의 상호작용을 3D time-independent finite difference 법을 개발하여 해석하였고, 선행연구와 비교를 통해 수치 모델을 검증하였다.

위 연구들의 결과들은 내부 유체의 도약, 도약에 의한 선체 운동변화처럼 큰 스케일 측면에서는 좋은 결과가 예상된다. 하지만, 탱크와 유체의 벽면에서의 경계 조건과 단순한 다상 모델 사용, 난류 영향을 고려하지 않음으로 인해 표면류 형태를 예측하는데 어려움이 있다. 또한, 포텐셜 이론 기반의 외란 가진 방식은 고체 외벽의 쇄파에 의한 유체의 박리(Separation)을 고려하지 못한다는 단점이 있다. 비선형 슬로싱을 연구한 S. Mitra [3] 의 연구를 제외하면, 대부분의 연구는 외란이 약한 경우하의 비점성, 선형 슬로싱 해석 연구이다. 하지만 실제 해양 부유체 내부 슬로싱은 선박의 운동, 해양 기후, 탱크의 형상에 따라 비선형성이 자주 나타난다.

따라서 본 연구에서는, 기존 연구에서 보고되지 않았던 3차원 실린더형 부유체 형상과 비선형성이 강한 자유표면의 슬로싱을 구현하였다. Volume Of Fluid (VOF) 기법을 적용하여 다상 유동을 구현하였으며, 외란으로는 비선형 파랑인 Stokes 5차 방정식을 이용하여 조파하였다. 결과는 비 정상상태 해석을 수행하여 슬로싱을 포함한 부유체의 2자유도(Heave, Pitch)운동 결과를 시간대 별로 비교하였다.

2. 수치 해석

2.1 지배 방정식

슬로싱과 파랑의 해석은 Navier-Stokes 방정식을 바탕으로 한 SST 난류 모델과 다상 유동 해석에는VOF모델을 이용하였다. Solver는 상용해석 프로그램인 CFX14.0 을 사용하였으며, 사용된 SST모델에 대한 설명은 참고문헌[5]에 잘 나타나 있다. 표면장력에 대한 영향은 무시할 수 있을 정도로 작다고 가정하였고, 비압축성, 비 정상상태, 점성유동을 고려한 지배 방정식은 다음과 같다. 식 (1) - (2) [6].

여기서, u_j는 속도, i,j는 텐서, ρ는 밀도, P는 압력, τ는 응력을 의미한다. 다상유동의 물리적 매개변수들은 다음과 같은 방법으로 계산된다. 식 (3) - (4).

여기서, α=1일 때 물, α=0일 때 공기이다. 강체의 운동은 선형적으로 작용하는 힘 F와 각 운동량π의 변화에 따른 영향을 받으며, 강체 운동은 다음과 같이 계산된다.

여기서 P는 선형 운동량, π는 각 운동량, m은 질량, θ는 오일러 각, I는 각축에 대한 질량 관성 모멘트 행렬을 나타낸다.

2.2 해석 모델 및 경계조건

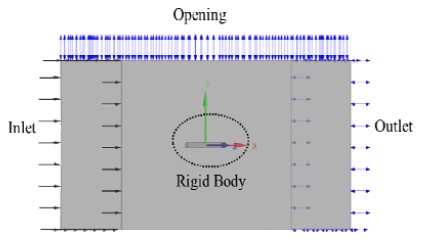
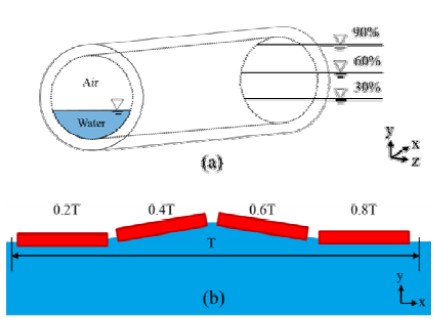
Figure 1은 내부와 외부 도메인을 나타내고 있다. 실린더 탱크의 기하학적 형상은 Li [7]의 결과에서 1.5m 파고하의 부유체 운동이 가장 활발했던 길이30m, 직경3.5m, 벽 두께 0.2m로 모델링하였으며, 실린더의 재질은 설계자에 의해 실제 환경에 견딜 수 있는 것으로 선택되어질 수 있다. 따라서 본 계산에서는 편의상 밀도가 물의 절반인 500kg/m³으로 가정하였다. Figure 2(a)와 같이 직경 기준으로 물을 30%, 60%, 90% 채워가며 슬로싱의 영향을 해석하였다. 해석에 사용된 격자는 Hexagonal 격자를 사용하였고, 2.14ⅹ10⁶ 노드와 2.09ⅹ10⁶개 요소들로 이루어져 있다. 공기의 물성치는 25℃, 밀도는 1.185 kg/m³ 로 주었다. 물의 밀도는 998 kg/m³, 실린더 벽면은 No-slip 조건, 검사체적 양쪽 벽면은 Free-slip 조건을 주었다. 윗면은 Openning 조건을 주었고, 대기압(1atm)을 설정하였다. Outlet은 상대 압력조건이며, Inlet 조건은 아래 수식의 Stokes 5^th 이론에 따라 x와 y방향의 속도 조건을 주었고, 각 방향의 성분은 다음과 같다. 식 (7) - (11) [8].

여기서, C0는 무차원 상수, ε은 무차원 파고, θ는 방향, g는 중력, c는 파속, k는 파수, H는 파고, d는 수심, t는 시간, x, y는 각각 수평축과 수직축을 나타낸다. Stokes 5^th 이론은 깊은 수심과 중간 수심에서 광범위하게 응용 될 수 있는 이론이다. 본 연구에서는 파고 1m, 파장 60m를 설정하였고, Ursell Parameter는 0.03이다. 이는 이론의 적용 한계치인26보다 적으므로 충분히 적용 가능하다.

본 연구에서는 실린더 내부 및 외부유체의 유동과 강체인 실린더의 거동이 커플링 되어 있다. 따라서 유체유동과 실린더의 상관을 효과적으로 수행하기 위하여 내부 사용자 함수 기능인 CEL을 사용하였으며, Newmark 법을 기반으로 내부 슬로싱의 영향, 외부 유체유동의 영향 및 실린더의 거동을 동시에 해석하였다.

Figure 1:

Analysis domain with boundary conditions

Figure 2:

Schematic diagrams of (a) water filling rate and (b) locations of a floater for a period T.

3. 해석 결과

3.1 시간대 별 부유체와 자유표면 가시화

Figure 2(b)는 파랑의 한 주기 T 동안 부유체와 파도 사이의 시간대별 상대위치를 나타내고 있고, 각 시간대별 부유체 의 운동과 내부 유체의 슬로싱은 Figure 3, 4와 같다. Figure 3은 앞의 경계 조건과 물성치, 해석 방법을 이용하여 해석한 결과를 x-y 단면으로 나타낸 그림이며, 시간대별 부유체 거동에 따른 유체의 분포를 체적비로 나타냈다. 파랑의 약 1주기 동안 부유체 거동을 2초 간격으로 나타내고 있고, (a)는 30%, (b)는 60%, (c)는 90% 물을 채웠을 때 결과이다. 여기서 부유체에 물이 채워질수록 흘수가 깊어지는 것을 확인할 수 있고, (a) 에서는 91s부터 발달한 유체 도약이 표면류로 발달하는 것을 확인 할 수 있다. (b)와 (c)의 경우 파랑의 자유표면 상, 하로 운동하고 있는 것을 관찰할 수 있고, Heave 운동이 (a)보다 활발함을 알 수 있다. 특히 (c)의 93s 시간대에서 부유체 윗부분으로 파랑이 쇄파되는 현상을 확인 할 수 있다.

Figure 3:

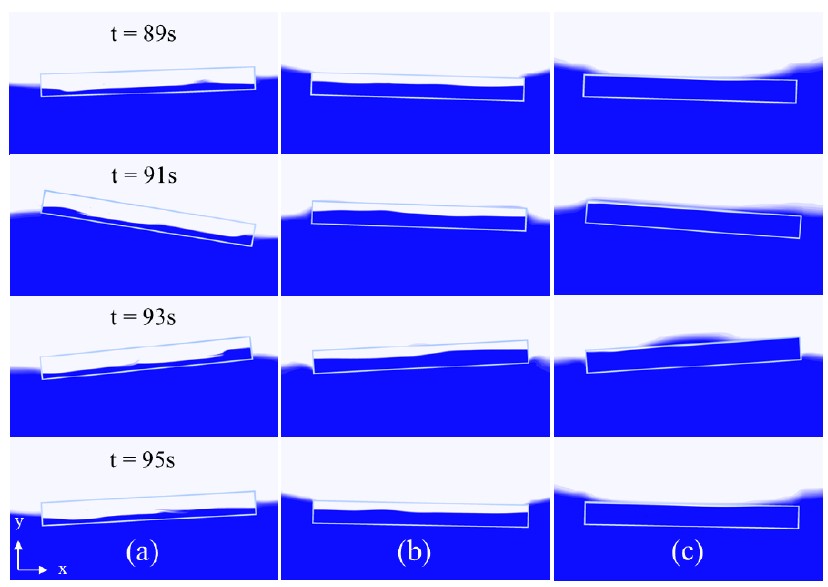
Visualization of cylindrical floater motions with sloshing (a) 30% filled cases, (b) 60% filled cases and (c) 90% filled cases.

Figure 4:

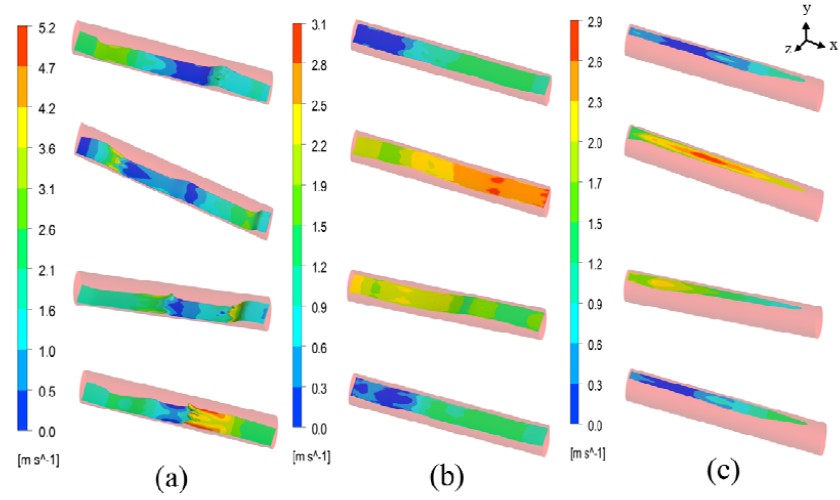
The time history of a sloshing in cylindrical tank and a velocity fields at free surfaces (a) 30% filled cases, (b) 60% filled cases and (c) 90% filled cases.

Figure 4는 Figure 3과 같은 시간대의 실린더 내부의 자유 표면과 속도장을 나타내고 있다. 표면의 슬로싱을 더 자세히 관찰하기 위해 z축 방향으로 2배 가량 비율을 늘려 표시 하였다. (a)의 경우 가장 슬로싱이 활발하며, (c)의 경우를 제외한 자유 표면은 강한 비선형성을 띄며 탱크 내 유체의 수심이 얕을수록 슬로싱이 활발한 것을 가시적으로 확인 할 수 있다. 표면류의 속도는 강한 슬로싱이 나타나는 (a)의 경우 95초에서 최대 5.2 m/s로 나타났고, (b) 의 경우 91초에서 최대 3.1m/s, (c)의 경우 역시 91초에서 최대 2.9 m/s로 물이 채워질수록 작아지는 경향을 나타냈다. 파랑과 강체 관성력 사이의 순간적인 상반 작용 영향에 따라 반드시 이러한 결과가 나타나지는 않지만, 이러한 경향성은 간단한 베르누이 법칙으로 설명이 가능하다. 물이 50% 이하로 채워지게 되면, 유체가 벽면을 타고 도약한 이후에 발달하는 표면류가 중력 방향으로 흐를 때, 실린더의 형상특성상 유체가 채워진 단면적이 좁은 원통 아랫부분으로 이동하게 되면서 속도가 빨라지게 된다. 반대로 50%이상 물을 채우게 되면 유체는 원통 윗부분으로 도약한 후 유입될 때 실린더 중앙 단면 쪽으로 넓게 유입되면서 표면류가 물이 채워질수록 점점 느려지는 경향을 나타내게 된다.

3.2 부유체 거동 해석

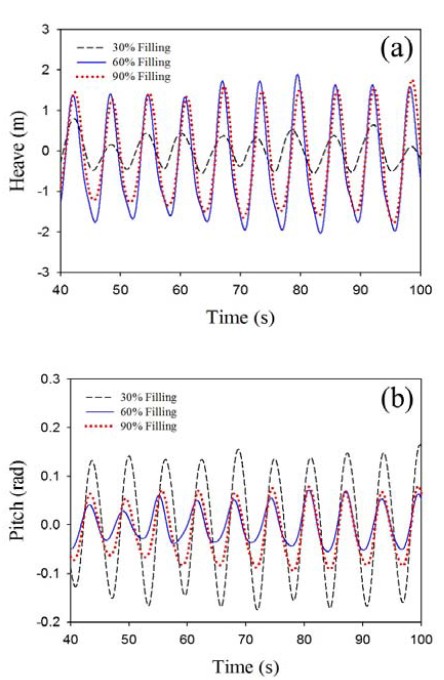
슬로싱 효과를 고려한 부유체 거동을 Heave 와 Pitch 운동으로 Figure 5에 표시 하였다. 40초에서 100초까지 60초 동안의 비 정상상태 계산 결과이며, (a)는 Heave, (b)는 Pitch 운동을 나타내었다. Heave 운동의 변위는 물이 30% 채워졌을 때 –0.5m~0.8m, 60% 일 때 –2.1m~1.9m, 90%일 때 –1.9m~1.7m로 나타났다. Pitch 운동의 변위는 30% 경우 68s, 60%와 90%경우에서 각각 82s 와 80s에서 최대로 나타났으며, 30% 경우에서 약 0.15 radian 으로 가장 크게 나타났으며, 다른 경우들 보다 약 2배가량 활발한 것을 볼 수 있다. 내부 유체의 비선형적인 운동과 파랑의 영향으로 주기성이 없는 경향을 확인 할수 있었고, 그림 2의 결과와 함께 해석해 보면 부유체 흘수 변화가 변화 할 때, 파랑의 자유 표면 부근의 영향 또한 부유체 Heave 운동에 영향을 줄 것 이라고 생각된다. 이에 따라 향후 연구에서는, 슬로싱 형태가 격렬해 짐에 따른 부유체의 거동 상관 관계에 대해 더 명확한 연구가 필요할 것으로 판단된다.

Figure 5:

The motions history of a cylindrical floater; (a) heave motion, (b) pitch motion.

4. 결 론

파랑에 대한 부유체 거동과 슬로싱 해석은 실린더 내부 및 외부유체의 유동과 강체인 실린더 거동의 3가지 요소가 완전히 결합된 해석방식이 요구된다. 본 연구는 외부유동의 영향을 고려한 부유체와 내부 슬로싱 거동을 결합시켰다. 슬로싱을 동반한 해양부유체 거동을 3차원, 비 정상상태로 해석하였고, 기존 연구에서 찾아보기 힘들었던 큰 스케일의 실린더 형상 내부의 슬로싱을 VOF 기법을 통하여 자유 표면과 파랑의 움직임을 정밀하게 구현하였다. 부유체 운동을 Heave와 Pitch 방향에 대해서 60초 동안 해석 하였고, 본 연구의 해석 방법과 결과는 Ptich 운동에 영향을 받는 Power Take Off unit (PTO) System을 이용한 파력 발전기, 혹은 Heave 모션에 영향을 받는 Aqua Buoy 형식의 파력 발전기에 응용 될 수 있고, 전력 생산 효율에 긍정적인 영향을 줄 것이라고 판단된다.

Acknowledgments

본 연구는 교육과학기술부, 한국연구재단의 지원으로 연구되었음. (NO.2010-0026578)

References

• Y. Kim, B. W. Nam, D. W. Kim, and Y. S. Kim, “Study on coupling effects of ship motion and sloshing”, Ocean Engineering, 34, p2176-2187, (2007). [https://doi.org/10.1016/j.oceaneng.2007.03.008]
• S. J. Lee, M. H. Kim, D. H. Lee, J. W. Kim, and Y. H. Kim, “The effects of LNG-tank sloshing on the global motions of LNG carriers”, Ocean Engineering, 34, p10-20, (2007). [https://doi.org/10.1016/j.oceaneng.2006.02.007]
• S. Mitra, C. A. Wang, J. N. Reddy, and B. C. Khoo, “A 3D fully coupled analysis of nonlinear sloshing and ship motion”, Ocean Engineering, 39, p1-13, (2012). [https://doi.org/10.1016/j.oceaneng.2011.09.015]
• C. H. Wu, and B. F. Chen, “Sloshing waves and resonance modes of fluid in a 3D tank by a time-independent finite difference method”, Ocean Engineering, 36, p500-510, (2009). [https://doi.org/10.1016/j.oceaneng.2009.01.020]
• F. R. Menter, M. Kuntz, and R. Langtry, “Ten years of industrial enperimence with the turbulence model”, Turbulence, Heat and Mass Transfer 4, p625-632, (2003).
• J. D. Anderson Jr, Governing Equations of Fluid Dynamics, Computational fluid dynamics-An Introduction, J. F Wendt, Ed. heidelberg:Springer, (1995).
• K. M. Li, N Parthasarathy, H. C. Yoon, and Y. W. Lee, “Numerical study on energy absorption of a floater for design of wave energy converter in ocean”, Journal of the Korean Society of Marine Engineering, 36(5), p635-644, (2012). [https://doi.org/10.5916/jkosme.2012.36.5.635]
• J. D. Fenton, “A fifth-order stokes theory for steady waves”, Journal of Waterway, Port, Coastal and Ocean Engineering, 111(2), p216-234, (1985). [https://doi.org/10.1061/(ASCE)0733-950X(1985)111:2(216)]