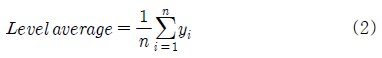Shape optimal design of a dust cover for ball joint of automotive steering system

1. 서 론

자동차의 수요가 급증함에 따라 자동차의 성능과 운전자의 안전에 대한 관심이 더욱 높아지고 있다. 또한 많은 종류의 부품을 필요로 하는 자동차의 특성 때문에 각 부품의 성능 및 안전성을 높이기 위해 많은 연구가 수행되고 있다[1]. 특히 컴퓨터의 성능 발전에 따라, 비선형적 거동을 하는 고무 부품에도 유한요소해석을 통한 평가가 활발히 적용되고 있으며 해석 결과의 신뢰성도 높아지고 있다. 본 연구에서는 자동차 조향장치의 볼 조인트에 사용되는 고무 재질의 더스트 커버에 대한 비선형 유한요소해석 및 최적설계를 다루고자 한다.

더스트 커버는 고무가 가지고 있는 밀봉성을 이용하여 모래 또는 물 등의 이물질로부터 조향장치의 볼 조인트를 보호하고, 볼 조인트 동작부의 윤활유를 밀폐하여 윤활성을 유지시키는 역할을 하는 중요한 부품이다[2][3]. 더스트 커버는 차축의 회전에 따라 인장, 압축, 굽힘의 복합적인 변형을 하게 되며, 고무끼리 서로 접촉하면서 운동하는 자체접촉도 일어나게 된다. 볼 조인트의 회전에 따라 반복하중을 받으면서 더스트 커버의 내구성이 떨어지게 되며, 손상에 따른 밀봉성 저하로 인해 볼 조인트부의 소음이 증가하거나 조향장치부의 결함이 발생할 수 있다[4]. 최근 조향장치용 볼 조인트의 작동조건은 더 많은 회전각도를 요구하고 있으며, 작동 시에 발생하는 최대응력의 크기가 성능을 결정하는 주요 척도이다. 최근에 Kim and Lee[5]는 주름형상과 항아리 형상의 두 종류의 더스트 커버에 대하여 유한요소해석을 통하여 조립상태와 작동상태를 해석하고, 밀봉 부위에서의 접촉압력과 몸통부의 응력을 비교 평가한 바가 있다.

본 연구에서는 상용 유한요소해석 프로그램인 MSC. MARC[6]를 이용하여 주름형상의 더스트 커버에 대하여 비선형 유한요소해석을 수행하여 응력을 평가하고, 다구찌 기법[7]을 이용하여 최대응력을 최소화하기 위한 형상최적설계를 수행하고자 한다. 최적설계를 위하여 다구찌 기법을 이용하면 직접탐색법을 이용한 수치적 최적화 기법에 비해 수렴성 문제와 반복해석에 소요되는 과도한 해석 시간의 문제를 방지할 수 있으며, 설계자가 설계인자의 영향도를 쉽게 평가하여 효율적으로 최적화를 수행할 수 있다는 장점이 있다.

Figure 1:

Section view of the dust cover assembly

2. 기존설계안의 해석

2.1 해석 방법

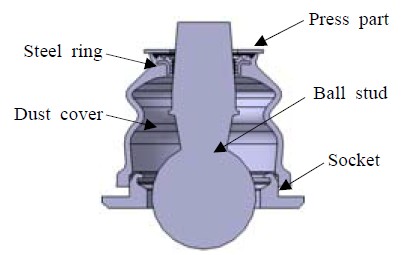
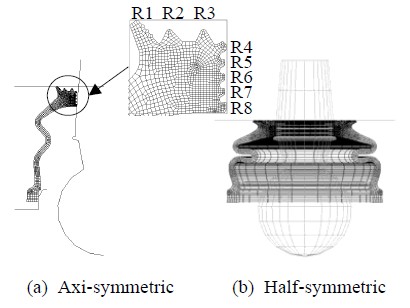
더스트 커버의 유한요소 모델에 대해 MSC. MARC를 사용하여 비선형 응력해석을 수행하였다. Figure 1은 주름형상의 더스트 커버의 단면 형상을 나타낸다[5]. Figure 2(a)에 더스트 커버의 밀봉 성능에 중요한 역할을 하는 리브(rib) 형상을 나타내었는데, 누름부(press part) 및 볼 스터드(ball stud)와 접하는 리브의 안쪽에는 강재 링(steel ring)이 매립되어 있다.

Figure 2:

Finite element model of the dust cover

Table 1:

Material property of the rubber (Ogden function)

더스트 커버의 재질은 T3-CR567인 고무이다. 이러한 고무재료는 초탄성 특성을 지니며, 기하학적 대변형 등의 비선형성의 존재로 해석 시에 해의 수렴이 매우 어렵고 해석에 많은 시간이 소요된다[8][9]. 이러한 재료의 특성을 묘사하기 위해 고무의 인장시험을 수행하고, 그 결과로부터 식 (1)과 같은 Ogden 함수[10]를 이용하여 고무의 물성치를 구하여 해석을 수행하였다. Ogden 함수로 정의할 때 필요한 고무의 물성치는 Table 1에 나타내었다. 강재 링은 일반 구조용 강의 물성치를 사용하였고 누름부와 소켓 및 볼 스터드는 강체로 가정하였다.

W = 변형 에너지

λ_i = 연신률

μ_i = 계수

α_i = 지수

K = 초기 체적탄성률

J = 부피비

전체 해석 과정은 총 두 단계로 구분하여, 1단계에서는 조립상태를, 2단계 해석에서는 작동상태를 해석하였다. 1단계의 조립상태에 관한 해석은 축대칭 모델을 구성하여 수행하였다. 조립상태에서는, 실제 조립조건을 감안하여 소켓(socket)이 3 mm 상승하고 누름부가 11.9 mm 하강하는 경계조건을 부여하였다. Figure 2(a)에 1단계 해석에 사용한 축대칭 유한요소모델을 나타내었으며, 절점 수가 1570개, 요소 수가 1314개이다. 2단계의 작동상태에 관한 해석에서는, 볼 스터드가 39° 굴절되는 작동조건을 감안하여 1단계의 축대칭해석 결과를 원주방향으로 180°확장하여 1/2대칭 모델을 구성하여 해석을 수행하였으며[5][11], 볼 스터드가 39° 굴절되도록 경계조건을 부여하였다. Figure 2(b)에 2단계 해석에 사용한 1/2대칭 유한요소모델을 나타내었으며, 절점 수가 36087개, 요소 수가 28908개이다.

2.2 해석 결과

앞 절에서 기술한 해석 방법에 기반하여 더스트 커버의 비선형 응력해석을 수행하였으며, 본 절에서는 그 결과를 요약하여 기술하고자 한다.

더스트 커버의 성능 중 하나인 밀봉성은 유한요소해석 결과로부터 구한 Figure 2에 표시된 리브 R1~R8에서 발생하는 접촉압력(접촉면의 수직응력)의 분포와 크기를 통해 평가하였다. 해석을 통해 계산된 조립상태와 작동상태의 접촉압력을 Table 2에 수록하였으며, Table 2에서 작동상태 A와 B는 각각 볼 스터드의 굴절방향과 반대방향 대칭면에 위치한 리브를 나타낸다. Table 2에서 볼 수 있듯이, 접촉압력은 누름부와 접하는 리브(R1~R3)에서 최외곽의 R1을 제외하고는 3.0 MPa 이상이다. 볼 스터드와 접하는 리브(R4~R8)에서는 최상부의 R4를 제외하고는 3 MPa 이상이며, 아래쪽의 R6~R8 에서는 8 MPa을 상회하는 것으로 나타났다. 그리고 작동상태의 접촉압력은 조립상태 대비 거의 변동이 없다. 따라서 리브는 볼 스터드 및 누름부와 잘 밀착하므로 더스트 커버의 밀봉성이 우수하고 누유가 발생하지 않는 것으로 판단된다.

Table 2:

Contact normal stress on the ribs

Figure 3:

Distribution of von-Mises stress for the initial design (Unit: MPa)

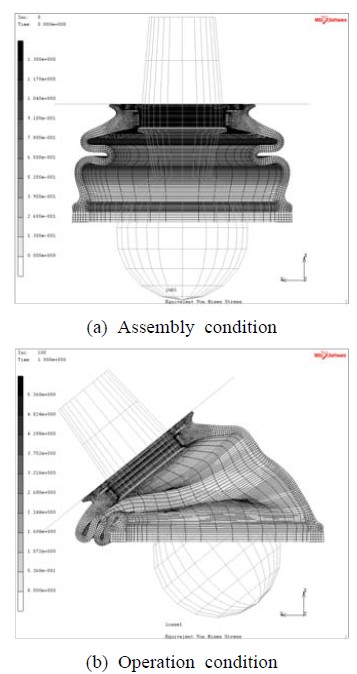
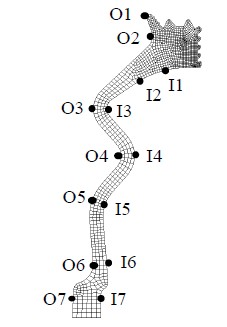
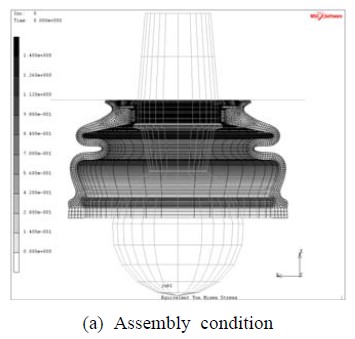
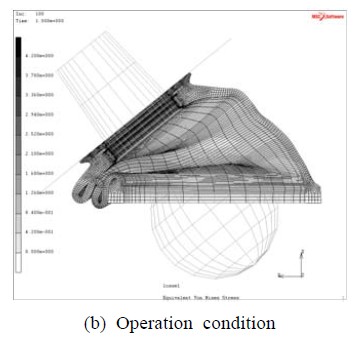
또 다른 평가요소인 내구성에 가장 큰 영향을 미치는 것은 고무에서 발생하는 최대응력의 크기이다. Figure 3(a)와 (b)에 조립상태와 작동상태의 변형형상 및 내표면과 외표면의 등가응력(von-Mises) 분포를 나타내었으며, 변형형상은 실제 더스트 커버의 거동과 유사하게 나타났다. Figure 4는 몸체부 대칭면의 외표면(O1~O7)과 내표면(I1~I7)을 따른 위치들을 나타낸다. 작동상태에서 내표면의 I2~I4, I4~I6 구간과 외표면의 O3~O5, O5~O7 구간에서 고무끼리 접촉하는 자체접촉이 발생하였다. 조립상태 및 작동상태 모두 O4 위치에서 최대응력이 발생하였고 작동상태에서의 최대응력이 조립상태보다 증가하는 것으로 나타났다. 최대응력은 조립상태에서는 1.30 MPa, 작동상태에서는 5.36 MPa로 재료의 인장강도인 18 MPa에 크게 미치지 못하는 것으로 나타났다. 하지만 볼 스터드의 좌우방향 굴절이 반복되는 조건에서의 내구수명 관점에서 볼 때 가능한 한 최대응력이 발생하는 위치의 응력을 저감시킬 필요가 있다. 최대응력이 발생한 O4 부분은 내표면의 I2~I4, I4~I6 구간의 자체접촉에 의해 압축을 받으면서 큰 응력이 발생하였다. 따라서 O4 부분의 두께와 형상의 설계인자가 최대응력에 영향을 미치는 중요한 인자임을 알 수 있다. 다음 장에서는 다구찌 기법을 통해 O4 위치의 최대응력을 저감시키기 위한 설계인자에 대한 최적설계안을 산출하였다.

Figure 4:

Cross section of the dust cover

3. 형상최적설계

3.1 다구찌 기법의 적용

본 장에서는 다구찌 기법을 사용하여 더스트 커버의 최대응력을 저감시키기 위한 최적설계안을 도출하였다.

평가 특성치로는 볼 스터드의 굴절방향에 따라 응력의 피크가 발생하는 위치의 응력을 고려하였으며[12], 작동상태에서 몸통부의 O4 위치에서 발생하는 최대 등가응력(S_max)으로 선정하였다. 다구찌 기법에서 특성치는 동특성, 망목특성, 망소특성, 망대특성으로 분류할 수 있으며, 본 연구의 특성치인 최대응력은 값이 작을수록 좋은 경우로 망소특성에 해당된다[13].

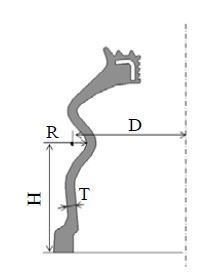
설계변수로는 Figure 5와 같이 최대응력이 발생하는 굴곡부 O4의 형상에 영향을 미치는 설계인자를 선정하였다. 설계인자는 굴곡부 O4의 곡률중심의 반경방향좌표(D), 굴곡부 O4의 곡률중심의 축방향좌표(H), 굴곡부 O4의 곡률반경(R), 몸체부의 두께(T)이다. Table 3에는 각 설계인자에 대한 수준을 나타내었으며, 기존설계를 2수준으로 설정하였다.

Figure 5:

Design variables of the dust cover

Table 3:

Level of design variables (Unit: mm)

설계인자 및 수준을 선정한 후에는 직교배열표를 선택해야 한다. 직교배열표는 선정된 설계인자를 배치하여 해석을 실시하고 각 설계인자의 효과를 파악하는데 사용하는 것으로 최소의 해석으로 최대의 효과를 얻을 수 있다[14]. 설계인자가 4개이며 수준이 3 개임을 고려하여 Table 4와 같은 L9(3⁴) 직교배열표를 사용하였다[15].

Table 4:

L9(34) orthogonal array

3.2 최적설계안의 해석 결과

Table 4에 나타낸 직교배열표에 따라 각각에 대한 해석을 수행하였다. 해석에 사용한 조건은 제2장과 동일한 조건을 사용하였다. 선정한 특성치에 대한 해석 결과를 Table 5에 나타내었다.

Table 5:

Result of characteristic(Smax)

Table 5에 나타낸 해석 결과를 이용하여 각 설계인자의 수준별로 특성치의 평균값을 계산하여 설계인자에 대한 효과를 분석하였다. 다구찌 기법에서 각 특성치의 평균값은 다음 식에 의해서 구할 수 있다[16].

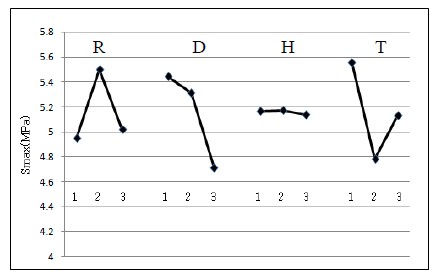
여기서 y_i는 i번째 경우의 평가특성 해석 결과를, n은 해당 수준에 대한 각 인자별 경우의 수를 나타낸다. 식 (2)를 사용하여 각 설계인자에 대한 평가특성의 수준별 평균값을 계산하여 Table 6에 표기하였다. 이러한 방법을 다구찌 기법에서는 요인효과 분석이라고 하며, Figure 6에 요인효과선도를 나타내었다.

Table 6:

Level averages of each design variable

Figure 6:

Graph of significant factors

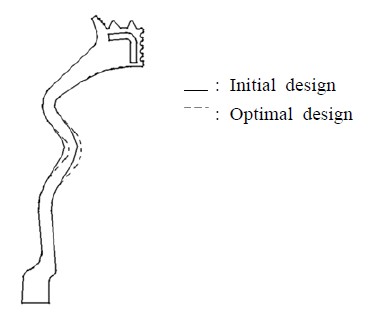
Figure 6을 보면 설계인자 D와 H는 3수준일 때 가장 우수한 결과를 나타내고 있으며, 설계인자 R은 1수준일 때 가장 우수한 결과를 나타내고 있다. 또한 설계인자 T는 2수준일 때 가장 우수한 결과를 나타내고 있다. 요인효과선도에서 기울기가 급할수록 민감도가 큰 설계변수이며, 평가특성의 수준별 평균값이 최소값을 가지는 수준을 최적값으로 선정하였다. Table 7에 설계인자들의 최적값을 나타내었으며, Figure 7에 초기설계(기존설계)와 최적설계의 형상을 비교하여 나타내었다.

Table 7:

Values of design variables of the initialand optimal design (Unit: mm)

Figure 7:

Initial and optimal shapes

이와 같이 결정한 최적설계안에 대하여 초기설계안과 동일한 방법으로 유한요소해석을 수행하였다. Figure 8(a)와 (b)는 최적설계안에 대한 조립상태와 작동상태의 변형형상 및 내표면과 외표면의 등가응력 분포를 나타내며, 최대응력은 조립상태에서는 1.40 MPa, 작동상태에서는 4.20 MPa 이다. 평가 특성치인 S_max는 최적설계에서 4.20 MPa로 초기설계의 5.36 MPa 대비 22 %의 감소 효과를 보였다.

Figure 8:

Distribution of von-Mises stress for the optimal design (Unit: MPa)

Figure 9:

Comparison of von-Mises stress of the initial and optimal design

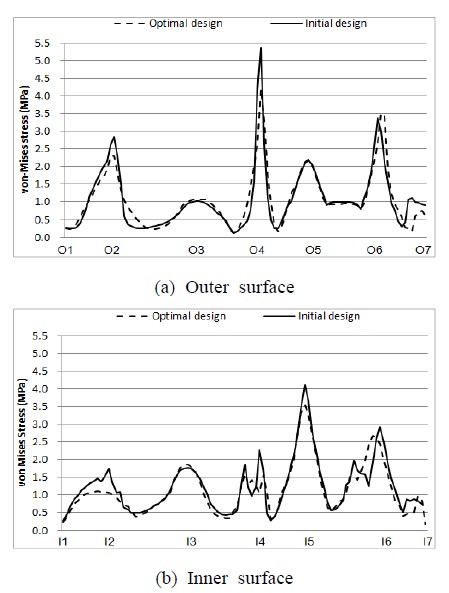
Figure 9(a)와 (b)는 초기설계안과 최적설계안의 해석 결과로부터 외표면과 내표면을 따라 추출한 응력 분포를 나타낸다. Figure 9를 보면, 굴곡부에서 피크가 나타나며 O4 부분에서 최적설계안의 응력이 초기설계안의 응력보다 감소한 것을 알 수 있다.

4. 결 론

본 연구를 통하여 도출한 주요 결과를 요약하면 다음과 같다.

1) 비선형 유한요소해석을 통하여 자동차 조향장치용 볼 조인트 더스트 커버의 조립상태 및 작동상태의 거동을 평가하는 방법을 제시하였다.

2) 윤활유의 밀봉에 영향을 미치는 리브에서의 접촉압력을 분석한 결과, 조립상태에서 리브가 누름부 및 볼 스터드에 밀착되며 작동상태에서도 조립상태 대비 밀봉성이 악화되지 않는 것으로 나타났다.

3) 작동상태에서의 최대응력은 고무의 자체접촉에 의해 압축되는 굴곡부에서 발생하며, 재료의 인장강도보다 크게 작은 것으로 나타났다.

4) 다구찌 기법을 사용하여 평가 특성치를 최대응력으로, 설계인자를 굴곡부의 형상변수로 선정하여 최적설계를 수행하였다. 도출된 최적설계안의 작동상태에서의 최대응력은 초기설계안 대비 22 % 감소되는 것으로 나타났다.

Acknowledgments

본 연구는 지식경제부․한국산업기술진흥원 지정 계명대학교 전자화자동차부품지역혁신센터(B0008866)의 지원에 의한 것이며, 김지호의 석사학위논문(“자동차 조향장치용 볼 조인트 더스트 커버의 응력해석 및 설계연구, 계명대학교 대학원”)을 개선한 것이다.

References

• Integration of transportation and IT Industry in 2030, National IT Industry Promotion Agency, (2009).
• S. H. Kim, Oh S. T., C. H. Lee, J. H. Lee, H. W. Lee, and H. Huh, “Finite element analysis for 3-D self-contact problems of C. V. joint rubber boots”, Transactions of the Korean Society of Mechanical Engineers A, 21(12), p2121-2133, (1997).
• C. W. Park, C. H. Park, S. D. Choi, and H. J. Choi, “Analysis of deformations of dust-seal in ball joint used for automobile part”, Proceedings of the Korean Society of Precision Engineering 2009 Spring Annual Meeting, p765-766, (2009), (in Korean).
• S. H. Kim, S. T. Oh, J. H. Lee, H. W. Lee, and H. Huh, “Stress analysis of C.V. joint rubber boots by finite element method and application to design modification”, Transactions of the Korean Society of Mechanical Engineers, 6(3), p123-137, (1998), (in Korean).
• J. H. Kim, and B. Y. Lee, “Nonlinear stress analysis of dust covers for the ball joint of automotive steering system”, Transactions of the Korean Society of Mechanical Engineers A, 37(10), (2013), (in Korean). [https://doi.org/10.3795/KSME-A.2013.37.10.1297]
• MSC, MARC User's Guide, MSC. Software, (2007).
• G. Taguchi, Taguchi Methods, Michigan USA: ASI, (1992).
• Y. D. Kwon, K. T. Roh, C. S. Ri, and S. P. Hong, “A study on the convergency of the finite element analysis of rubber using numerical differentiation method”, Transactions of the Korean Society of Automotive Engineers, 7(5), p141-153, (1999), (in Korean).
• J. E. Mark, B. Erman, and F. R. Eirich, Science and Technology of Rubber, 2nd ed, New York: Academic, (1994).
• U. C. Baek, M. H. Cho, and J. S. Hawong, “Material properties for reliability improvement in the FEA results for rubber parts”, Transactions of the Korean Society of Mechanical Engineers A, 35(11), p1521-1528, (2011), (in Korean). [https://doi.org/10.3795/KSME-A.2011.35.11.1521]
• T. H. Kang, Y. S. Kim, and I. K. Kim, “An analysis of rubber dust-cover for automotive parts”, Transactions of the Society of CAD/CAM Engineers, 10(5), p375-379, (2005).
• W. D. Kim, C. S. Woo, and S. W. Han, “Finite element analysis and fatigue life evaluation of automotive rubber insulator”, Elastomers and Composites, 33(3), p168-176, (1998).
• B. Y. Lee, and H. W. Lee, “Shape optimal design of an automotive pedal arm using the Taguchi method”, Journal of the Korean Society of Precision Engineering, 24(3), p76-83, (2007), (in Korean).
• J. Kang, J. M. Lee, J. H. Kang, Y. C. Park, and H. C. Park, “Optimization of a gate valve using orthogonal array and kriging”, Journal of the Korean Society of Precision Engineering, 23(8), p119-126, (2006), (in Korean).
• J. H. Kim, Finite Element Analysis and Optimal Design of a Roller Rail for a Refrigerator, M.S. Thesis, Department of Mechanical Engineering, Keimyung University, Korea, (2007), (in Korean).
• S. B. Lee, Application of Taguchi Methods Using Minitab, 1^st ed., Gunpo, Korea: Eretec, (2006), (in Korean).