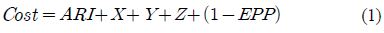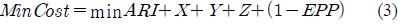Layout design optimization of pipe system in ship engine room for space efficiency
Recent advanced IT made layout design fast and accurate by using algorithms. Layout design should be determined by considering the position of equipment with satisfying various space constraints and its component works with optimum performance. Especially, engine room layout design is performed with mother ship data, theoretical optimal solution, design requirements and several design constraints in initial design stage. Piping design is affected by position of equipment seriously. Piping design depends on experience of designer. And also piping designer should consider correlation of equipment and efficiency of space. In this study, space evaluation method has been used to evaluate efficiency of space. And also this study suggested object function for optimal piping route, Average Reservation Index(ARI), Estimated Piping Productivity(EPP) and with modified space evaluation method. In this study, optimum pipe routing system has been developed to reflect automated piping route with space efficiency and experience of piping designer. Engine room is applied to the design of the piping in order to confirm validity of the developed system.
Keywords:
Layout Design, Optimum Design, Engine Room, Average Reservation Index(ARI), Estimated Piping Productivity(EPP)1. Introduction
Initial ship design of engine room is usually performed based on preceding design data such as reference ship data, theoretical optimum solutions, requirement items and design constraints. And the designed data are used for the next design stage. Moreover, designers modify the layout under consideration of equipment performance analysis and the evaluation of equipment operators. Finally, an optimum layout is selected after evaluation under designer’s knowledge and experience.
To perform the layout design more effectively, researches about room arrangement in ship have been carried out [1][2]. Hills et al. [3] studied effective design method for section layout or initial structural layout. Especially, Penteado et al. [4] conducted optimum layout of equipment of chemical process plant considering safety. Many researchers have focused on the optimization of room layout and plant equipment layout.
However, in company with equipment layout, pipe layout is also important. Because pipe arrangement is unconditionally affected from equipment layout, pipe path could not be determined before equipment arrangement. Also, even though equipment layout is confirmed, it is often modified due to high expenses of pipe [5]. Thus, the optimization method of pipe path has difficulty in performing the design effectively in short time using computer. If there is the design system satisfying the various design requirements, the efficiency of pipe design could be increased. Pipe path design highly depends on the experiences of designer. In the pipe design, considering the correlation among equipment and room efficiency is difficult. It is necessary to develop the optimum design system satisfying the design requirements.
Therefore, in this paper pipe design system is proposed to optimize the pipe path for engine room
2. Theory for optimum pipe path design
2.1 Optimum arrangement evaluation methodology
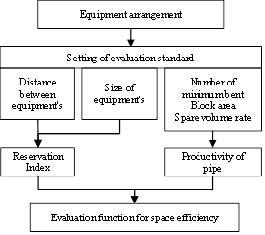
Generally, machinery equipment is evaluated and produced under the established standards such as standardization, departmentalization and ergonomics. The standards for evaluation of equipment arrangement system consist of the following objection functions: the maximization of convenience for operations and maintenances; the minimization of equipment size; Estimate Pipe Productivity (EPP); the maximization of Estimated Link Practicability (ELP); Reservation Index; evaluation of cost function. Under the assigned algorithm, initial layout design is calculated, and finally optimum layout is selected to minimize the cost function. For the design optimization of equipment arrange, easy, productivity, size of equipment, interference, and locations of elements are considered. Designed equipment’s from experienced designers are compared and evaluated for optimum arrangement alternatives under the considerations. Besides, pipe ducting between unit equipment is considered from the initial stage of arrangement. Figure 1 illustrates algorithm for flowchart to evaluate the space efficiency according to equipment arrangement.
2.2 Fuzzy theory
Fuzzy theory is introduced by Prof. Zadeh at UC Berkley in 1965 [6]. Fuzzy theory expresses uncertainty of phenomenon in itself. The theory expresses the real approximate and inexact state more effectively than traditional logic system. Because the evaluation of equipment arrangement contains many uncertain terms such large/small, far/near, often/sometimes, and emergency/ normal, Fuzzy theory can be effectively applied for the evaluation. Previous set theory based on boolean logic explain that a specific object is belong to set A (1, true) or not to set A (0, false). On the other hand, from fuzzy set theory based on Fuzzy theory, specific set A can be expressed by the number from 0(fully excluded) to 1 (perfectly included). For example, for a set A of tall people, Crips set and Fuzzy set are compared as shown in Figure 2.
Fuzzy set A attached to universal set U can be defined as follow:
where, UA(x) is membership function of x in A. Membership function assigns each element of X number from 0 to 1.
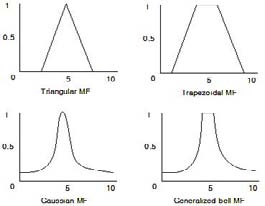
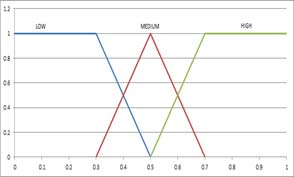
The simplest membership functions are composed by using lines. The simplest is triangular membership function which is composed of three points of triangle. Membership function of trapezoidal has flat shape at top, which is cut shape of truncated triangle curve. These line functions are easy for calculation. Besides, there are Gaussian membership function and generalized bell membership function as shown in Figure 3.
The evaluation items of descriptive language can be included in the computer program, by expressing vague terms using Fuzzy function and organizing from Fuzzy rules. Moreover, from the Fuzzy inferences, designers can quantify the evaluation standards as well as can evaluate arrangement alternatives fast and easy.
Layout design for evaluation algorithm
A Comparison of Fuzzy Set and Crisp Set
Membership Functions
2.3 Shortest path search algorithm
Shortest path means the shortest path among the paths existing between two stationary points on graph. At direction graph the initial peak and final peak on path are called source and destination, respectively. Shortest path problem is divided according to the selection of source and destination. Edsger Dijkstra [7] proposed Dijkstra algorithm which search shortest path from source to every destination. The shortest path length obtained by conducting algorithm is stored into array. If all the stationary points are included in the subset of stationary points, the subset of shortest path has shortest path. Disjkstra algorithm investigates the shortest path by maintaining the set which is composed of start peak and shortest path already known. Firstly, only start peak is included in the set expressed array. Secondly, it searches the shortest path by selecting point which is shortest point from stationary point to among points which in not included in set of stationary points, also by including only shortest points into the set. The shortest points from start stationary point to arbitrary stationary point are stored into set using array. When all the points are included in the set, the set have points having the shortest points from start stationary point to all points through these procedures [8].
Moreover, Hart et al. [9] developed A* search algorithm which combines heuristic method and formal method, in order to estimate of the best route from start point to destination node. A* algorithm guarantees searching shortest path on graph and it performs under minimum computation. From the research of Hart et al. [9], admissibility and optimality properties of A* algorithm are verified.
Therefore, because A* algorithm guarantees short time and optimization, in this study A* algorithm is used for the optimum system considering room efficiency as well as pipe path optimization.
3. Optimum pipe path search system
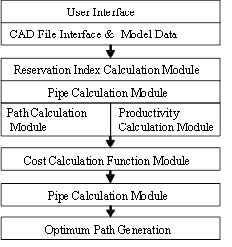
Optimum pipe path system is developed using Fuzzy theory and path search algorithm. Figure 4 illustrates system organization for optimization of pipe path.
Flow chart of equipment arrangement evaluation system
3.1 Fuzzy modeling for pipe path optimization
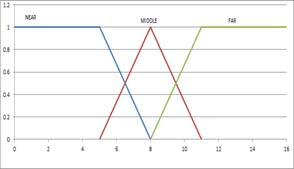
Eight Fuzzy rules are determined in order to estimate reservation index. Based on the rules, Fuzzy inference system contains input and output. Distance, input Fuzzy function as shown in Figure 5 consists of linear Fuzzy function. Reservation index, output is composed of Fuzzy function as shown in Figure 6. Fuzzy rules for inference of Reservation Index are determined as shown in Table 1. Goodness of fit concerning input can be obtained from the intersection of two propositions at sound area. Next, inference result of each rule can be found by applying these good nesses of fit to consequent Fuzzy set, reservation index. Then, final inference result can be determined by accumulating each rule. In fact, the final inference value Z is obtained by using center of gravity method [10].
3.2 Pipe path searching algorithm
In this study, pipe path searching system is pro posed and A* algorithm is used to calculate optimum pipe path. The applied A* algorithm guarantees the searching shortest path with minimum calculation using heuristic information. Using heuristic information, the modified cost accelerates searching to the direction of the objective node, instead of exploring all direction. Consequently, it reduces time consuming for the search of small node and edge, and the exploring velocity
Fuzzy set for distance.
Fuzzy set for Reservation Index
increases.
In this study, cost function for the generation of optimum pipe path can be expressed as follows:
where, ARI denotes Average Reservation Index; X, Y, Z represent manhattan distance; EPP stands for Estimated Pipe Productivity. Upon it, optimum pipe paths are calculated using Reservation Index of equipment as well as using heuristic information of distance between nodes. In this study, the objective function for optimum pipe path search is defined as cost function and it can be formulate as follow:
3.3 Optimization application for pipe path
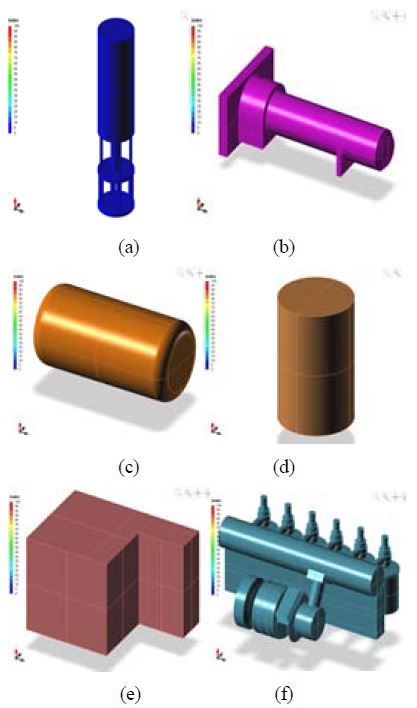
In this study, to validate the proposed optimization pipe path system, the pipe path generation of engine room is conducted. Table 2 demonstrates the lists of equipment used for pipe path generation as well as size and influence distances. Equipment shapes are displayed in Figure 7.
Fuzzy rules for inference of Reservation Index
List of Equipment and Influence Distance
Modeling for unit equipment: (a) pump; (b) Generate; (c) Tank type 1; (d) Tank type 2; (e) 2nddeckgenerator;(f)Engine
4. Results and Discussion
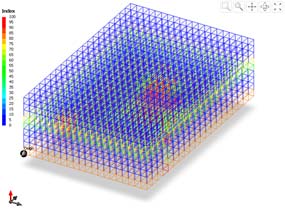
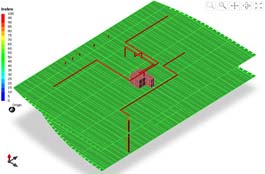
Optimum pipe path generation of engine room is conducted in order to validate the effectiveness of algorithm proposed in this research. In order to define the space, cell size and number of cells are defined as shown in Table 3. Figure 8 illustrates the defined design space.
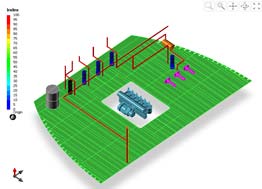
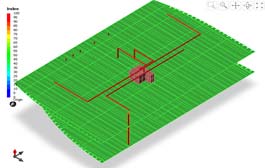
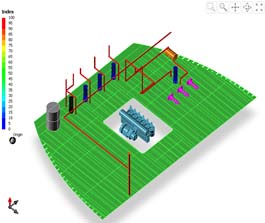
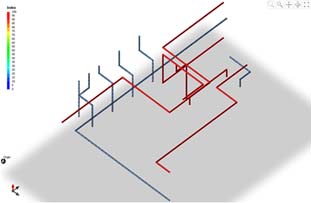
Figure 9-10 show the design from the experiences of designers. Figure 11 illustrates the reservation index. Optimized designs using pipe design system are shown in Figure 12-13. And corresponding reservation index is shown in Figure 14. Average reservation index according to each design method is compared in Table 4. The average reservation index before pipe generation shows low value of 23.04. The average reservation index of design based on designer’s experience and of optimized design are 51.41 and 51.36, respectively. Figure 15 illustrates the differences of design based on designer’s experience and optimized design.
Cell size and number of cells of design space
Definition of design space
Pipe Arrangement of Deck 1
Pipe Arrangement of Deck 2
Reservation Index of design
Pipe Arrangement of Deck 1
Pipe Arrangement of Deck 2
Comparison of Average Reservation Index for Design Alternatives
Reservation Index of Optimized design
After applying the layout optimization (Changed the Pipe)
From the Figure 15, it is observed that the total length of the pipe and number of bent part are the same before and after the optimization. Therefore, it is clear that the design from the proposed system not have effect on EPP, so that the pipe condition is the same. However, from the ARI the efficiency of the room is improved.
5. Conclusions
In this paper, Fuzzy theory and A* search algorithm was applied for optimization of pipe route of engine room in the design stage of ship. From the research the following conclusions were made:
1) A* algorithm is used for the search of optimum path of pipe for engine room, and the analysis results showed short calculation time and optimization of path.
2) The efficiency of A* algorithm was maximized by joining the traditional evaluation factors such as ARI and EPP.
3) The proposed methodology can be effectively used for the pipe design in engine room.
Acknowledgments
This research was financially supported by the Ministry of Education, Science Technology (MEST) and National Research Foundation of Korea (NRF) through the Human Resource Training Project for Regional Innovation
Notes
References
-
J. P. Hope, “The process of naval ship general arrangement design and analysis”, Naval Engineers Journal, 93(4), p29-38, (1981).
[https://doi.org/10.1111/j.1559-3584.1981.tb00657.x]
-
A. Cort, and W. Hills, “Space layout design using computer assisted methods”, Naval Engineers Journal, 99(3), p249-260, (1987).
[https://doi.org/10.1111/j.1559-3584.1987.tb02136.x]
- W. Hills, and M. Wels, “An efficient compartmentation method for use in preliminary ship design”, Proceedings of ICCAS'89, (1989), p141-153.
-
F. D. Penteado, and A. R. Ciric, “An MINLP approach for safe process plant layout”, Industrial & Engineering Chemistry Research, 35(4), p1354-1361, (1996).
[https://doi.org/10.1021/ie9502547]
- J.-K. Park, Development of Evaluation System for Machinery Arrangement in Engine Room, M.S. Thesis, Department of Naval Architecture, Pusan National University, Korea, (2002), (in Korean).
-
L. A. Zadeh, “Fuzzy sets”, Information and Control, (1965), 8(3), p338-353.
[https://doi.org/10.1016/S0019-9958(65)90241-X]
-
E. W. Dijkstra, “A note on two problems in connection with graphs”, Numeriche Mathematik, 1(1), p269-271, (1959).
[https://doi.org/10.1007/BF01386390]
- W.-B. Ku, Data Structure Realized Using C Language, Seoul, Korea: Insolmedia Publisher, (2001), (in Korean).
-
P. E. Hart, N. J. Nilsson, and B. Raphael, “A formal basis for the heuristic determination of minimum cost paths in graphs”, Systems Science and Cybernetics, IEEE Transactions on, 4(2), p100-107, (1968).
[https://doi.org/10.1109/TSSC.1968.300136]
- S.-K. Oh, Fuzzy Model and Control System by C Programming, Seoul, Korea: Naeha Publisher, (2002), (in Korean).