유기랭킨사이클용 반경류터빈의 예비설계 및 성능분석
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
유기랭킨사이클의 열역학적 효율에 큰 영향을 미치는 구성요소는 터빈이다. 일반적으로 유기랭킨사이클에서 팽창과정은 작동유체의 급격한 물성치 변화를 수반하므로 터빈의 설계에 많은 어려움이 따른다. 그러므로 효율이 우수한 터빈의 개발을 위해서는 정밀한 터빈의 예비설계가 요구된다. 반경류터빈의 효율은 loading과 flow 계수에 큰 영향을 받으므로 터빈의 예비설계에서 이러한 변수의 선정이 매우 중요하다. 그러나 기존의 성능곡선으로부터 loading과 flow 계수를 선정하는 고전적인 방법을 이용할 경우 정밀한 예비설계를 기대하기 힘들다. 그러므로 본 연구에서는 로터 깃의 개수와 열역학적 설계조건으로부터 loading과 flow 계수를 산출하는 방법을 제시하였다. 본 연구에서 제시한 예비설계모델을 이용하여 예비설계를 수행한 결과는 공신력 있는 상용예비설계프로그램을 이용한 결과와 비교하여 만족스러운 것을 확인하였다. 또한 예비설계모델의 정확성을 검증하기 위해 예비설계한 반경류터빈에 대한 수치해석을 수행하였으며 효율을 제외한 대부분의 변수들이 예비설계조건을 비교적 충족하는 것을 확인하였다.
Abstract
The major component with a significant impact on the thermodynamic efficiency of the organic Rankine cycle is the turbine. Many difficulties occur in the turbine design of an organic Rankine cycle because the expansion process in an organic Rankine cycle is generally accompanied by a dramatic change in the working fluid properties. A precise preliminary design for a radial inflow turbine is hard to obtain using the classic method for selecting the loading and flow coefficients from the existing performance chart. Therefore, this study proposed a method to calculate the loading and flow coefficient based on the number of rotor vanes and thermodynamic design requirements. Preliminary design results using the proposed models were in fairly good agreement with the credible results using the commercial preliminary design software. Furthermore, a numerical analysis of the preliminary design results was carried out to verify the accuracy of the proposed preliminary design models, and most of the dependent variables, with the exception of the efficiency, were analyzed to meet the preliminary design conditions.
Keywords:
Radial inflow turbine, Preliminary design, Organic rankine cycle키워드:
반경류터빈, 예비설계, 유기랭킨사이클1. 서 론
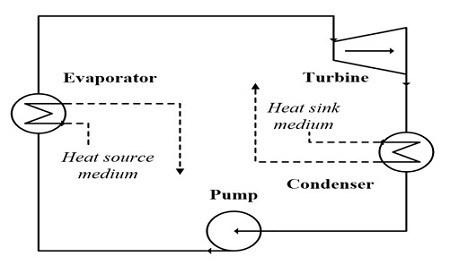
최근 강화되고 있는 환경규제와 화석연료의 고갈 문제로 인하여 유기랭킨사이클(ORC; Organic Rankine Cycle)에 대한 관심이 고조되고 있다. 유기랭킨사이클의 구성요소는 증발기, 터빈, 응축기, 펌프이며 이러한 구성은 고전적인 증기랭킨사이클과 다르지 않으나, 유기랭킨사이클은 비등점이 낮은 유기냉매 또는 탄화수소화합물을 작동유체로 사용하므로 열원의 온도가 비교적 낮을지라도 터빈의 구동에 필요한 고압의 기체를 확보할 수 있다. 그러므로 그동안 경제성의 이유로 회수하지 않았거나 고전적인 증기랭킨사이클로 회수하지 못하였던 태양열, 해양온도차, 지열 및 공장 및 발전소의 폐열과 같은 저온의 열원으로부터 유기랭킨사이클을 이용하여 발전을 하려는 시도가 이어지고 있다.
유기랭킨사이클의 열역학적 효율에 큰 영향을 미치는 구성요소는 터빈이다. A. Whitfield et al. [1]과 R. H. Aungier [2]는 성능이 우수한 반경류터빈의 개발을 위하여 예비설계의 중요성을 강조하며 예비설계기법을 정립하였다. 그러나 이러한 설계기법은 작동유체의 물성치 변화를 무시할 수 있을 경우에 유효하므로 유기랭킨사이클과 같이 일반적으로 팽창과정에서 물성치가 극심히 변화하는 유기랭킨사이클의 반경류터빈의 설계에는 적합하지 않다.
유기랭킨사이클용 터빈의 내부유동에서 물성치의 극심한 변화는 반경류터빈의 설계에 큰 어려움을 야기시키며, 이에 따라 Han et al. [3] 그리고 E. Sauret et al. [4] 등은 유기랭킨사이클용 반경류터빈의 예비설계에 공신력 있는 상용예비설계프로그램인 RITAL을 이용하였다. RITAL은 작동유체의 물성치 변화에 대응하기 위해 NIST Refprop과 연동하여 반경류터빈의 예비설계를 수행할 수 있으며, 손실모델을 이용하여 예비설계한 반경류터빈의 설계점 및 탈설계점에 대한 성능을 예측할 수 있다. 그러나 RITAL은 입력변수 선정에 어려움이 많으며 실제기체를 작동유체로 선정할 경우 응답속도가 늦고 매우 고가이다. 이에 따라 Kim [5]은 H. Moustapha et al. [6]이 정립한 설계기법을 응용하여 빠르고 사용하기 쉬운 유기랭킨사이클용 반경류터빈의 예비설계프로그램인 RTDM (Radial Turbine Design Modeler)을 개발하였으며, 반경류터빈의 예비설계에 이용하여 만족스러운 결과를 얻은 바 있다[7][8].
한편, E. Sauret et al. [4]는 터빈 성능 분석에서 점성력을 고려한 3차원 유동해석의 중요성을 강조한 J. Harinck et al. [9]의 연구에 따라 초임계사이클에 해당하는 지열발전용 반경류터빈을 RITAL을 이용하여 예비설계하고 3차원 유동해석을 통하여 그 성능을 분석하였다. RITAL을 반경류터빈의 예비설계에 이용할 경우 예비설계조건인 flow와 loading 계수의 선정이 터빈의 효율 결정에 중요하다. 그러나 E. Sauret et al. [4]의 연구에서는 이러한 예비설계조건을 바람직하게 결정하지 못하였으므로 합리적인 예비설계조건 산출에 대한 연구가 필요하며, 수치해석에 있어서도 명확하게 개선되어야 할 부분들이 발견되었다.
본 연구에서는 반경류터빈의 예비설계조건을 산출하는 모델을 제시하고 이를 바탕으로 개발된 RTDM을 이용하여 유기랭킨사이클용 반경류터빈을 예비설계하였다. 반경류터빈의 열역학적 운전조건과 설계조건은 E. Sauret et al. [4]의 연구에 따르며 RTDM을 이용한 예비설계의 결과는 동일한 설계조건으로 RITAL을 이용하여 예비설계한 결과와 비교하였다. RTDM을 이용하여 예비설계한 반경류터빈의 성능은 3차원 유동해석을 적합하게 수행하여 그 성능을 분석하였다.
2. 예비설계
2.1 작동유체 및 열역학적 사이클
반경류터빈의 예비설계에 앞서 작동유체 및 열역학적 사이클의 구성 등은 E. Sauret et al. [4]의 연구를 따른다. 작동유체는 R143a이며 주요 물성치는 Table 1과 같다. 유기랭킨사이클의 구성은 Figure 1에 나타낸 바와 같이 기본밀폐사이클이며 지열발전의 열역학적 사이클 및 터빈의 설계조건은 Table 2와 같다. 이러한 운전조건에서 R143a는 사이클의 순수출력과 터빈크기에 있어 최상의 성능을 나타낸다[10].
Main properties of R143a
Schematic of basic closed organic Rankine cycle
Thermodynamic data from R143a ORC cycle
2.2 예비설계조건
RITAL을 이용할 경우 flow와 loading 계수의 선정이 반경류터빈의 예비설계결과에 큰 영향을 미친다. E. Sauret et al[4]는 H. Moustapha et al. [6]이 제시한 반경류터빈의 성능곡선으로부터 효율(ηts) 90%에 해당하는 flow와 loading 계수를 각각 0.215, 0.918으로 선정하였다. 그러나 RITAL을 이용하여 예비설계한 터빈의 효율은 76.8%에 불과하였으며 3차원 터빈형상에 대한 최적화를 수행하였음에도 불구하고 그 성능을 개선시키는 것에는 실패하였다.
한편 RTDM에서 flow와 lading 계수는 예비설계조건이 아니며 예비설계과정에서 도출되는 종속변수이다. 일반적으로 성능이 검증된 반경류터빈에 있어서, 로터입구 상대속도 각도는 20~40°이다[1][6]. 로터 깃의 개수(Nr)와 로터입구 상대속도의 각도(β4)는 밀접한 관계가 있으며, A. Whitfield et al. [1]은 식 (1)과 같은 실험식을 제안하였다.
| (1) |
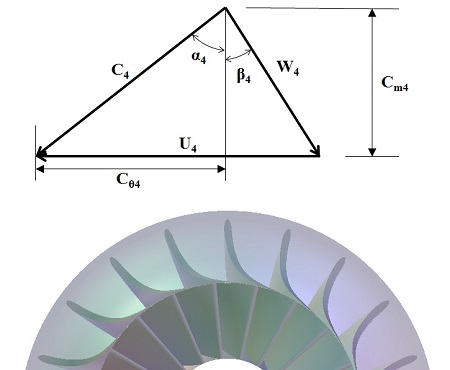
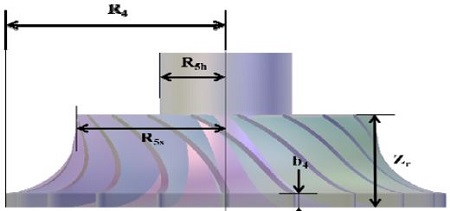
H. Moustapha et al. [6]이 제시한 로터입구 속도삼각형에 대한 최적화 모델은 식 (2) ~ (6)과 같다. 로터 깃의 개수를 선정하여 식 (1)로부터 로터입구 상대속도의 각도를 계산하면, 식 (2) ~ (6)에 의해 터빈 로터의 loading 계수(ψ)와 Figure 2에서 묘사한 로터 입구 속도삼각형의 각 변에 대한 비가 완성됨을 알 수 있다.
Rotor inlet velocity triangle
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
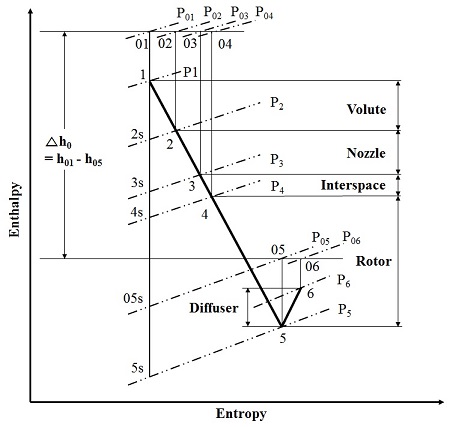
한편 터빈의 효율에는 total to total 효율(ηtt)과 total to static 효율(ηts)이 있으며, 각각은 Figure 3로부터 식 (7)과 식 (8)과 같이 정의된다. 이 중 total to static 효율을 식 (8)과 같이 근사할 수 있으며, 성능이 우수한 반경류터빈의 로터입구 원주속도와 분출속력의 비(υ)는 0.7이므로[1][2][6], 식 (1) ~ (6)을 통하여 계산된 loading 계수를 이용하여 total to static 효율을 근사할 수 있다. 또한 υ을 상수로 선정하였으며 사이클에 대한 열역학적 조건으로 분출속력(Cs)가 결정되므로 식 (9)로부터 로터 입구의 원주속력(U4)을 산출할 수 있다. 이를 식 (4) ~ (6)에 대입하여 로터 입구의 속도삼각형을 완성할 수 있다.
Temperature-entropy diagram for a radial inflow turbine
| (7) |
| (8) |
| (9) |
여기서
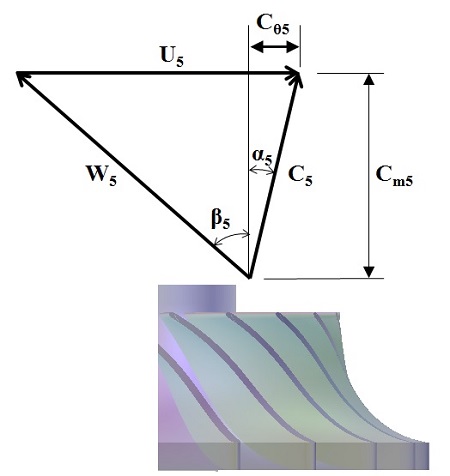
R. H. Aungier [2]는 적당한 자오선 속도비(ξ)에 대한 범위로 1.0 ~ 1.5를 제시하였으며, H. Moustapha et al. [6]은 자오선 속도비를 1로 선정할 것을 제안하였다. 여기서 자오선 속도비는 Figure 2와 Figure 4로부터 식 (10)과 같으며 이를 1로 선정하면 로터 입구의 자오선 속력이 식 (6)에 의해 결정되므로 로터 출구의 자오선 속력을 계산할 수 있다. flow 계수(φ)는 로터 출구의 자오선 속력과 로터 입구의 원주속력의 비이며 식 (11)로부터 flow 계수를 쉽게 산출할 수 있다.
Rotor exit velocity triangle
| (10) |
| (11) |
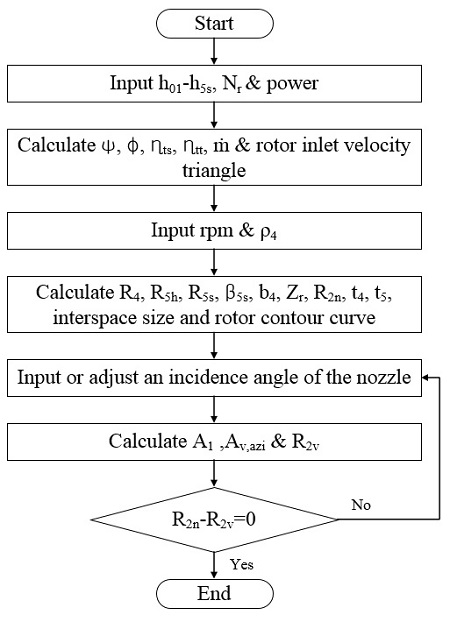
RTDM은 식 (1) ~ (11)을 기초로 로터 깃의 개수와 터빈의 열역학적 운전조건에 대한 엔탈피강하량을 입력변수로 하여 flow와 loading 계수를 계산할 수 있다. RTDM에 대한 주요 알고리즘은 Kim [5]의 연구와 같으며 flow와 loading 계수의 산출 이후 RTDM은 볼류트, 노즐, 로터에 대한 형상을 결정한다. RTDM에 적용한 알고리즘에 대한 흐름도는 Figure 5와 같다.
Flow chart of the preliminary design for RTDM
RTDM을 이용한 예비설계의 조건은 E. Sauret et al. [4]의 연구와 동일하다. 등엔트로피 엔탈피강하량(h01-h5s)은 Table 2의 열역학적인 조건으로부터 Nist Refprop을 이용하여 산출하면 29,740 [J/kg]이며, 목표 출력과 로터의 회전수는 각각 400 [kW]와 24,250 [rev/min]이다. 본 연구에서는 로터 깃의 개수는 20개로 선정하였다. 이를 요약하면 Table 3과 같다.
Input parameters of RTDM
2.3. 예비설계결과
RTDM에 의해 결정된 반경류터빈의 성능 및 형상에 대한 주요수치를 RITAL의 결과와 비교하면 Table 4와 같다. 여기서 Table 2의 조건을 제외하면 RITAL의 입력변수로는 ψ, φ, Nr, Nn 그리고 ηts가 있으며, 이들은 RTDM의 계산결과와 동일하게 입력하였다. Table 4를 살펴보면, 노즐 입구 반경을 제외하고 RTDM와 RITAL의 결과가 대동소이하다. 이는 RTDM이 채택하고 있는 예비설계에 대한 각종 모델과 터빈형상에 대한 구속조건들이 신뢰성이 검증된 반경류터빈의 상용예비설계프로그램인 RITAL과 유사하며, 예비설계에 대한 성능은 두 프로그램이 큰 차이가 없음을 의미한다.
Comparison between results of RTDM and RITAL
Table 4에서 비교적 큰 차이를 보이는 노즐 입구 반경은 두 프로그램이 선정한 노즐의 입·출구 반경비가 다르기 때문이다. RTDM은 노즐의 입·출구 반경비로 1.4를 선택하고 있는 반면, RITAL은 1.25를 default 값으로 선택하고 있다. R. H. Augier [2]가 제안한 적당한 노즐의 입·출구 반경비는 1.1에서 1.7이므로 두 프로그램 모두 적당한 반경비를 선택하고 있다. 그러나 노즐 깃의 코드 길이가 보다 긴 것이 로터의 유동 입사각을 조정하는 것에 보다 유리하므로 RTDM은 RITAL에 비하여 비교적 큰 반경비를 선정하고 있다. 또한 성공적으로 유기랭킨사이클용 반경류터빈에 대한 예비설계를 수행한 Kim et al. [7][8]의 연구에서도 노즐의 입·출구 반경비를 1.4로 선택하였다. 그러므로 Table 4에서 비교적 큰 차이를 보이는 노즐 입구 반경은 터빈의 성능에 큰 영향을 미치지 않은 형상변수로 판단된다.
Nomenclature of rotor stage
한편 Table 4의 RITAL 결과를 살펴보면, H. Moustapha et al. [6]이 제안한 반경류터빈의 성능곡선을 이용하여 ψ, φ을 선정할 경우 발생 가능한 예비설계의 불확실성이 사라진 것을 알 수 있다. E. Sauret et al. [4]은 반경류터빈의 성능곡선으로부터 90% 효율(ηts)에 해당하는 ψ, φ을 각각 0.215, 0.918으로 선정하고 RITAL을 이용하여 반경류터빈의 예비설계를 수행하였으나, 예비설계결과는 효율 76.8%에 불과하였다. 그러나 본 연구에서 제시한 예비설계모델 및 RTDM을 이용한다면 로터 깃의 개수를 조정하여 ηts, ψ, φ을 예측할 수 있으며 그 결과를 공신력 있는 상용프로그램인 RITAL을 이용하여 확인한 바에 의하면 성능곡선을 이용한 고전적인 방법의 불확실성이 사라진 것을 확인할 수 있다.
본 연구의 예비설계조건으로부터 로터 깃의 개수에 따른 ηts, ψ, φ을 RTDM을 이용하여 산출하면 Table 5와 같다. 자오선 속도비를 1로 선정할 경우 Table 5의 결과는 작동유체 및 터빈의 설계조건에 따라 종속적이지 않으므로 H. Moustapha et al. [6]이 제안한 성능곡선을 이용하여 예비설계를 수행하는 고전적인 방법과는 달리 본 연구에서는 Table 5의 변수를 반경류터빈의 예비설계에 대한 초기값으로 사용할 것을 제안한다.
Total to static efficiency, flow and loading coefficient according to the rotor blade number
3. 수치해석
J. Harinck [9]은 터빈의 성능분석에 있어 점성력을 고려한 3차원 유동해석의 중요성을 강조하였다. 본 연구에서는 상용수치해석프로그램인 CFX V13.0을 이용하여 예비설계조건에 대한 터빈의 성능을 확인하였다.
3.1 3차원 형상
Table 4에 보인 바와 같이 본 연구의 유동조건으로부터 RTDM과 RITAL을 이용하여 예비설계한 반경류터빈의 형상에 대한 차이가 사소하다. 본 연구에서는 RTDM을 이용하여 예비설계한 반경류터빈에 대한 수치해석을 수행하였다. 이 때 RTDM의 신뢰성을 수치해석을 통하여 검증하기 위하여 3차원 터빈형상에 어떠한 최적화도 수행하지 않았다.
E. Sauret et al. [4]은 RITAL의 예비설계로부터 노즐, 로터, 디퓨져에 대한 수치해석을 수행하였으나 본 연구에서는 RTDM을 이용하여 예비설계한 볼류트, 노즐, 로터에 대한 수치해석을 수행하였다. 볼류트는 Figure 3과 식 (7) ~ (8)에 나타낸 바와 같이 반경류터빈의 성능에 영향을 미치는 요소인 반면 디퓨져는 반경류터빈의 성능에 어떠한 영향을 미치지 않는다. 그러므로 3차원 수치해석에서 본 연구와 같이 볼류트, 노즐, 로터에 대한 수치해석을 수행하는 것이 합리적이다. 단, Kim [5]의 연구와 같이 수치해석에 있어 수렴성 개선을 위하여 회전도메인인 로터를 유동방향에 있어 최종도메인으로 설정하지 않고 로터 후단에 가상의 비회전 도메인을 추가 적용하였다. 이 영역은 Figure 7에 보인 바와 같이 환형이며, 이 영역의 전체 높이는 로터 전체 높이의 20%에 불과하다.
3D view of the overall geometry
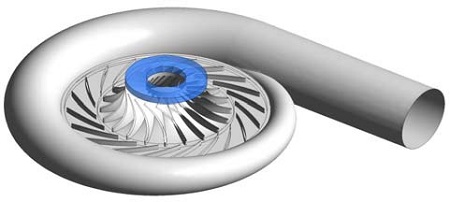
Figure 7은 수치해석에 적용한 전체 도메인에 대한 그림이다. RTDM의 예비설계 결과로부터 볼류트와 로터 후단의 환형 도메인은 CATIA V5R19, 그리고 노즐과 로터는 BladeGen V13.0을 이용하여 형상화하였다.
3.2 난류모델과 격자
난류모델과 벽처리방법에 따라 격자에 대한 y+ 값이 적합하게 선정되어야 한다. 회전체 유동의 적합한 난류모델은 k-ω와 SST 난류모델이 있으며[11], E. Sauret et al. [4]이 수치해석에서 k-ε난류모델을 선정한 것과는 달리 본 연구에서는 SST 난류모델을 이용하였다.
오메가-난류방정식을 기반으로 하는 난류모델에 한하여 CFX는 벽처리 방법으로 저레이놀즈수 방법을 지원한다. 점성효과를 자세하게 모사하기 위하여 점성저층을 직접 계산하는 저레이놀즈수 방법을 선택할 경우 y+ 값은 2 이하로 조밀한 격자를 형성하여야 한다[11]. 이러한 저레이놀즈수 방법은 저레이놀즈수 유동에 적합하다.
한편 항상 저레이놀즈수 방법이 벽함수 방법보다 높은 정확성을 나타내는 것은 아니다[12][13]. 또한 본 연구의 로터 입구 측의 유동조건으로부터 레이놀즈수를 산출하면 6.6e+6에 달하므로 고레이놀즈 유동에 해당한다. 그러므로 본 연구에서는 벽처리방법으로 벽함수를 선정하였다. 이와 같은 경우 y+ 값은 300 이하로 격자를 형성하여야 한다[11].
E. Sauret et al. [4]은 벽함수를 벽처리 방법으로 선정하였음에도 불구하고 y+ 값은 약 700으로 기준치를 초과하는 격자를 형성하였다. 본 연구에서는 Table 6에 나타낸 바와 같이 CFX 13.0 modeling guide [11]에 따라 y+ 300 이하의 격자를 형성하였다. Table 6에 나타낸 격자수는 격자 의존성을 점검하여 결정된 최종 격자수이다. 노즐과 로터도메인은 TurboGrid V13.0을 이용하여 정렬격자를 형성하였으며, 볼류트 도메인은 Ansys Meshing V13.0을 이용하여 비정렬격자를 형성하였다. 그 밖에 전단력을 고려하지 않은 로터 후단의 가상영역은 ICEM CFD V13.0을 이용하여 128,000개의 정렬격자를 형성하였다. Figure 8은 볼류트, 노즐, 로터에 형성한 격자계를 나타내고 있다.
Mesh information
3D view of the overall mesh
3.3 경계조건 및 수치해석모델
경계조건은 예비설계조건인 Table 2와 예비설계결과인 Table 4로부터 터빈 입구조건으로는 질량유량 16.90 [kg/s]와 전온도 413 [K], 그리고 출구조건으로는 정압 1835 [kPa]로 설정하였다. 로터의 회전수는 예비설계조건인 24,250 [rev/min]이다. 로터 후단의 가상영역을 제외한 볼류트, 노즐, 로터의 모든 벽면은 점착(no-slip) 조건이 부여되었으며, 회전체와 비회전체 사이의 인터페이스에는 frozen rotor 인터페이스 조건을 설정하였다.
E. Sauret et al. [4]이 동일 조건에서 Peng Robinson 상태방정식을 사용한 것과는 달리 본 수치해석에 사용한 실제기체방정식은 Aungier Redlich Kwong 상태방정식이다. Aungier Redlich Kwong 상태방정식은 임계점 근방의 상태량에 대한 정확성을 향상시킨 모델이므로[2][14], Peng Robinson 상태방정식보다 본 연구와 같이 초임계사이클용 반경류터빈의 수치해석에 보다 적합하다.
3.4 수치해석결과
수치해석결과는 실험자료와 비교되어야 하나, 실험이 수행된 것이 아니므로 예비설계결과와 수치해석의 결과를 비교하였다. RTDM을 이용한 예비설계조건 및 결과와 CFXV13.0을 이용하여 수치해석을 수행한 결과를 비교하면 Table 7과 같다.
Comparison between results of RTDM and CFD
예비설계한 터빈형상에 대한 어떠한 최적화를 수행하지 않았음에도 불구하고 예비설계의 결과와 수치해석의 결과는 효율을 제외한다면 비교적 잘 일치한다. 특히 전엔탈피강하량과 식 (12)에 의해 산출되는 터빈 출력에 대한 예비설계와 수치해석 결과의 차이는 약 1.26% 이하이다. E. Sauret et al. [4]가 동일한 조건에서 예비설계를 수행하고 형상에 대한 최적화를 수행한 반경류터빈의 수치해석결과에서 출력이 예비설계조건을 약 7% 상회하는 것을 고려할 때 본 연구에서 그 차이가 뚜렷하게 개선되었다. 즉, 예비설계에 있어서 보다 정확하게 flow와 loading 계수를 산출하고 수치해석에서 볼류트 영역을 노즐 그리고 로터영역과 함께 고려하며, 난류모델에는 회전체유동에 적합한 SST 모델을 사용하고 적합한 격자와 상태방정식을 이용함으로서 수치해석결과를 크게 개선할 수 있다.
| (12) |
그러나 Table 7에서 나타낸 바와 같이 온도의 변화량과 효율에 있어서 본 연구에서 수치해석결과의 개선을 위하여 적용한 일련의 조치에도 불구하고 E. Sauret et al. [4]의 연구에 비교하여 개선되지 않았다. E. Sauret et al. [4]에 의하면 기존의 상태방정식을 이용한 수치해석에서 미소한 온도차이가 발생하게 되며 터빈의 효율은 온도에 민감한 상태량이므로 수치해석상의 효율이 큰 차이를 보인다. 이러한 기존 상태방정식의 오차는 터빈의 팽창과정이 임계점 근처에 있거나 터빈의 팽창비가 증가할수록 심화된다. 그러므로 터빈에 요구되는 팽창비가 과도하여 초음속유동 혹은 초음속유동에 근접한 유동이 발생할 경우와 터빈의 운전조건이 임계점 근처에 형성될 경우, 반경류터빈의 수치해석을 위해서는 기존 상태방정식과 비교하여 보다 정밀한 Peng Robinson Stryjek Vera cubic 혹은 Span & Wagner 상태방정식 등이 수치해석프로그램에 적용되어야 할 것으로 보인다[15].
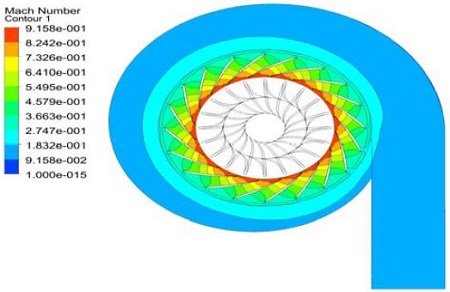
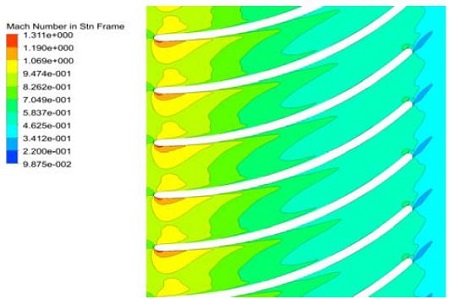
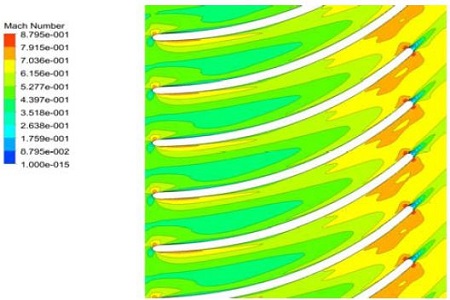
터빈의 유로에서 초음속유동이 발생할 경우 큰 유로손실과 구조적인 문제가 발생하기도 한다. Figure 9은 볼류트와 노즐의 마하수 분포이며 최고 마하수는 약 0.92이다. Figure 10와 Figure 11은 각각 로터부의 절대속력과 상대속도에 대한 마하수를 나타내고 있다. 절대속력의 경우 로터깃 앞날(leading edge)에서 국부적으로 초킹이 발생하였으나 그 영역이 크지 않다. 또한 상대속력의 경우 로터깃 뒷날(trailing edge)부분에서 마하수 0.87에 해당하는 최고속력을 가진다.
Mach number distribution of the stator
Mach number for absolute velocity of the rotor
Mach number for relative velocity of the rotor
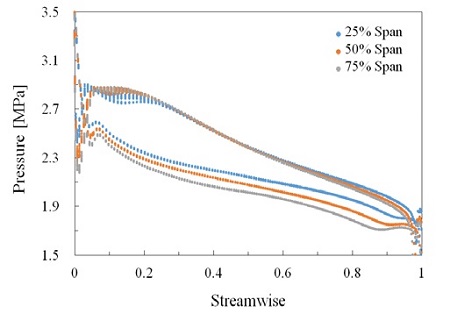
로터 깃의 압력면과 흡입면에 작용하는 압력차이가 크거나 유동방향으로 압력변화가 급격할 경우 로터 깃에 구조적인 문제가 발생할 수 있다. Figure 12는 유동방향에 따른 로터 깃의 압력 분포이며 특이사항이 발견되지 않았다. 그러나 이러한 구조적인 문제는 차후 구조해석에서 엄밀히 다루어져야 할 사항이다.
Blade loading at three different rotor blade heights
4. 결 론
유기랭킨사이클의 효율에 큰 영향을 미치는 구성요소는 터빈이다. 일반적으로 유기랭킨사이클에서 팽창과정은 작동유체의 급격한 물성치 변화를 수반하므로 터빈의 설계에는 큰 어려움이 따른다. 그러므로 성능이 우수한 터빈의 개발에는 정밀한 예비설계가 요구된다.
반경류터빈의 예비설계에서 loading 과 flow 계수의 선정은 매우 중요하나 성능곡선으로부터 이러한 계수를 선정할 경우 정밀한 예비설계를 기대하기 힘들다. 본 연구에서는 로터 깃의 개수와 열역학적 설계조건으로부터 loading과 flow 계수를 산출하는 방법을 제시하였다. 본 연구에서 제시한 방법을 이용하여 반경류터빈을 예비설계를 수행하였으며, 그 결과를 공신력 있는 상용예비설계프로그램을 이용하여 확인한 결과, 본 연구에서 제안한 예비설계기법이 만족스러운 것을 확인하였다.
유기랭킨사이클용 반경류터빈의 예비설계결과는 점성효과를 고려한 3차원 수치해석을 수행하여 그 성능 및 내부유동을 확인하였다. 수치해석에 사용한 상태방정식은 임계점 부근에서 정확성을 향상시킨 Augier Redlich Kwong 방정식이며 난류모델은 회전체 유동에 적합한 SST 모델이다. 수치해석결과는 본 연구에서 참고한 기존 연구와 비교하여 터빈효율을 제외한 대부분의 유동조건에 대하여 만족스러운 결과를 얻었다. 그러므로 본 연구에서 제시한 예비설계모델과 이를 적용하여 개발한 예비설계프로그램을 이용하여 비교적 적합한 초임계 유기랭킨사이클용 반경류터빈을 예비설계할 수 있다는 것을 확인할 수 있었다.
그러나 본 연구와 같이 초임계사이클용 반경류터빈에 대한 보다 엄밀하고 신뢰할 수 있는 수치해석결과를 얻기 위해서는 유동조건에 보다 적합한 상태방정식을 수치해석에 적용할 필요가 있다. 터빈에 대한 수치해석에서 터빈효율은 온도에 민감한 특성을 가지나 터빈의 팽창과정이 임계점 근처에 형성되거나 팽창비가 과도하여 초음속유동 혹은 초음속유동에 근접한 유동조건이 발생할 경우 기존의 상태방정식은 온도변화를 정확하게 예측하지 못한다. 그러므로 초임계사이클 혹은 초음속용 터빈 성능을 수치해석을 통하여 정확하게 예측하기 위해서는 Helmholtz 에너지를 이용한 Span & Wagner 상태방정식 혹은 Peng Robinson Stryjek Vera cubic과 같은 정밀한 상태방정식이 수치해석에 적용될 필요가 있으며, 이러한 상태방정식에 따른 초임계사이클 혹은 초음속용 터빈의 수치해석에 대한 연구가 추가적으로 필요할 것으로 보인다.
Nomenclature
| A : | : Area |
| C : | : Absolute velocity |
| M : | : Molar mass |
| N : | : Blade number |
| NBP : | : Normal boiling point |
| P : | : Pressure |
| R : | : Radius |
| T : | : Temperature |
| U : | : Circumferential velocity |
| W : | : relative velocity |
| Z : | : Overall Height |
| h : | : Enthalpy |
| : | : Mass flow rate |
| t : | : Blade thickness |
| Π : | : Pressure ratio |
| α : | : Absolute flow angle |
| β : | : Relative flow angle |
| η : | : Efficiency |
| ν : | : Velocity ratio |
| ξ : | : Meridional velocity ratio |
| ρ : | : Density |
| τ : | : Torque |
| φ : | : Flow coefficient |
| ψ : | : Loading coefficient |
Subscript
| 0 : | :Stagnation state |
| 00 : | :Stagnation state at position 0 |
| 1 : | :Position of the volute inlet |
| 2 : | :Position of the volute exit and nozzle inlet |
| 3 : | :Position of the nozzle exit and interspace exit |
| 4 : | :Position of the interspace exit and rotor inlet |
| 5 : | :Position of the rotor exit and diffuser inlet |
| 6 : | :Position of the diffuser exit |
| azi : | :Azimuth angle |
| c : | :Critical state |
| m : | :Meridional component |
| n : | :Nozzle |
| r : | :Rotor |
| s : | :Isentropic or shroud |
| ts : | :Total to static |
| tt : | :Total to total |
| v : | :Volute |
| θ : | :Tangential component |
Acknowledgments
본 연구는 2013년도 지식경제부의 재원으로 한국에너지 기술평가원(“OTEC 발전용 신개념 저온작동유체 및 반경류터빈의 기술개발”, No. 20133030000110)의 일부 지원으로 이루어진 성과이며 이에 관계자 여러분께 감사드립니다.
References
- A. Whitfield, and N. C. Baines, Design of Radial Turbomachines, NY, USA, John Wiley and Sons Inc, (2006).
- R. H. Aungier, Turbine Aerodynamics, NY, USA, ASME Press, (2006).
-
S. J. Han, and J. B. Seo, “20kW turbine development for OTEC system”, Journal of the Korea Society for Fluid Machinery, 17(6), p38-43, (2014), (in Korean).
[https://doi.org/10.5293/kfma.2014.17.6.038]
-
E. Sauret, and Y. Gu, “Three-dimensional off-design numerical analysis of an organic Rankine cycle radial- inflow turbine”, Journal of the Applied Energy, 135, p202-211, (2014).
[https://doi.org/10.1016/j.apenergy.2014.08.076]
- D. Y. Kim, A Study of the Development of a Preliminary Design Program for Organic Rankine Cycle Radial Inflow Turbines, Ph.D. Dissertation, Department of Marine System Engineering, Korea Maritime and Ocean University, Korea, (2015), (in Korean).
- H. Moustapha, M. F. Zelesky, N. C. Baines, and D. Japikse, Axial and Radial Turbines, Vermont, USA, Concepts NREC, (2003).
-
D. Y. Kim, H. K. Kang, and Y. T. Kim, “The development of a preliminary designing program for ORC radial inflow turbines and the design of the radial inflow turbine for the OTEC”, Journal of the Korean Society of Marine Engineering, 38(3), p276-284, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.3.276]
-
D. Y. Kim, and Y. T. Kim, “Design of a 100kW-class radial turbine for ocean thermal energy conversion using R32”, Journal of the Koran Society of Marine Engineering, 38(9), p1101-1105, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.9.1101]
-
J. Harinck, D. Pasquale, R. Pecnik, J. van Buijtenen, and P. Colonna, “Performance improvement of a radial organic Rankine cycle turbine by means of automated computational fluid dynamic design”, Proceedings of the Institution of Mechanical Engineers, Part A: Journal of the Power and Energy, 227(6), p637-645, (2013).
[https://doi.org/10.1177/0957650913499565]
-
E. Sauret, and A. S. Rowlands, “Candidate radial –inflow turbines and high-density working fluids for geothermal power systems”, Journal of the Energy, 36(7), p4460-4467, (2011).
[https://doi.org/10.1016/j.energy.2011.03.076]
- ANSYS CFX 13.0 Modeling Guide.
- J. G. Bak, J. U. Kim, Y. S. Gang, L. S. Cho, and J. S. Cho, “Comparative study on the near-wall treatment methods for heat transfer prediction of gas turbines nozzle guide vane”, Proceedings for the KSME Fall Conference, p985-990, (2013), (in Korean).
- J. K. Choi, and H. T. Kim, “A study of using wall function for numerical analysis of high Reynolds number turbulent flow”, Journal of the society of Naval Architects of Korean, 47(5), p647-655, (2010), (in Korean).
- ANSYS CFX 13.0 Theory Guide.
- P. Colonna, S. Rebay, J. Harinck, and A. Guardone, “Real-gas effects in ORC turbine flow simulations: influence of thermodynamic models on flow fields and performance parameters”, Proceedings of the European Conference on Computational Fluid Dynamics, p1-18, (2006).