수중 글라이더의 운동특성을 고려한 동역학 모델링 및 운동성능 해석

1. 서 론

최근 육지자원의 자원 부족과 새로운 자원 탐사를 위해 해양탐사가 늘어가는 추세이다. 특히 연안을 벗어나 대양과 심해탐사 연구가 증가하여 이를 효율적으로 수행할 수 있는 탐사장비의 수요가 증가하고 있다. 현재 해저 케이블 매설과 같은 수중작업을 할 수 있는 ROV(Remotely Operated Vehicle)가 많이 활용되고 있으나 모선과 케이블로 연결되어 작업 반경에 한계가 있다. 또한 모선과 케이블연결 없이 자율 주행하여 해양탐사를 할 수 있는 AUV(Autonomous Underwater Vehicle)가 해양탐사에 많이 사용되고 있으나 내부 전원용량 한계로 인한 운용시간의 제약이 있다. 이로 인해 긴 시간동안 공간의 제약 없이 대양과 심해를 탐사할 수 있는 탐사장비의 개발필요성이 더욱 커지고 있다.

비교적 긴 시간동안 자율적인 운항을 통해 수중을 탐사하는 장비인 수중 글라이더는 일반적인 무인 잠수정과는 달리 별도의 추진기를 사용하지 않고 내부의 부력엔진과 자세제어기를 이용하여 추진력을 얻게 된다. 추진력을 얻기 위하여 연속적인 에너지 소모가 아닌 잠항과 부상을 위한 부력변경과 자세변경 시에만 제한적으로 에너지를 소모하여 에너지 효율을 극대화 시킬 수 있다.

현재 개발되어 상용화된 수중 글라이더는 ONR(Office of Naval Research)의 지원을 받아 Washington Univ.에서 제작된 Seaglider, Scripps에서 제작한 Spray, Wood Hole 해양학연구소에서 개발한 Slocum, ANT에서 개발한 Littoral Glider가 있다[1]-[4]. Seaglider의 경우 CTD센서만 사용할 경우 220일간 운용이 가능하며 Spray 역시 CTD만 사용할 경우 330일 가량 운용이 가능하다. 또한 연안의 빠른 조류에서도 사용할 수 있는 Littoral Glider는 약 2 kts의 속도로 운용할 수 있다[3].

본 논문에서는 선행된 연구에서 개발된 Littral Glider와 같이 비교적 빠른 속도를 얻기 위하여 내부 이동 질량체와 피스톤 하우징 형태의 부력엔진을 장착한 수중 글라이더를 무게 대비 큰 체적 제어비를 가지도록 설계하였다. 또한 본 논문은 수중 글라이더 개발을 위한 기초 연구로써 운동특성을 해석하기 위한 수중 글라이더의 비선형 6자유도 운동방정식을 전개하였으며 PMM시험과 CFD해석을 이용해 추정된 유체력 계수를 이용하여 운동 시뮬레이션을 수행 하였다. 또한 운동 시뮬레이션에 수중 글라이더의 시스템 응답특성을 고려하기 위해 부력엔진 피스톤의 이동 속도와 자세제어기 내부질량의 이동속도를 각각 유압, 기계적 모델링을 수행하여 운동 시뮬레이션에 반영하였다. 수행된 운동 시뮬레이션의 결과를 분석하여 부력엔진과 자세제어기의 운동에 따른 수중 글라이더의 운동 특성을 확인하였다.

2. 시스템 구성

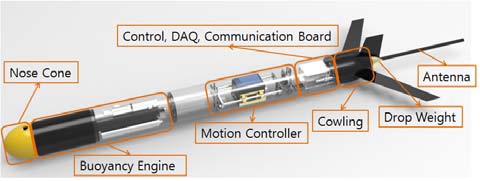
비선형 6자유도 운동 모델링에 사용된 수중 글라이더의 시스템 구성은 Figure 1과 같다. 어뢰형태의 외형을 가지며 수중 운동 시 유체의 저항을 최소화하기 위해 Myring profile[5]을 이용하여 설계 되었다. 노즈콘은 부력엔진 피스톤 하우징과 체결되어 있으며 피스톤 하우징은 외부에 노출되어 있다. 피스톤 하우징은 피스톤의 이동에 따라 해수의 유입이 자유롭도록 설계되어 부력을 조절할 수 있도록 설계되었으며 동체와의 체결 시 수밀을 위해 O-ring을 이용한 수밀방법을 이용하였다. 동체는 좌굴해석과 내압시험을 통해 목표수심의 수압을 견딜 수 있도록 설계하였으며 내부는 부력엔진의 유압탱크와 전동모터 등 피스톤 위치를 제어하기위한 장치들과 자세제어기, 제어 및 통신용 보드로 구성되어 있다. 카울링 끝부분에 드롭 웨이트를 설계하여 비상상황 시 긴급부상이 가능하도록 설계하였다.

Figure 1:

Configuration of underwater glider

3. 동역학 모델링

3.1 좌표계 설정

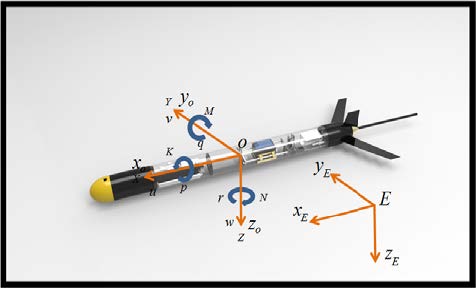
부력엔진과 자세제어기의 운동에 의해 발생되는 수중 글라이더의 운동 해석을 위해서는 동역학 모델이 필요하며 모델링을 수행하기 위해 Figure 2와 같이 좌표계를 설정하였다. 수중 글라이더의 운동을 나타내기 위해 일반적으로 수중 운동체에 사용되는 지구고정좌표계 Ex_Ey_Ez_E와 선체고정좌표계 Ox_Oy_Oz_O를 사용 하였으며 선체고정좌표계의 원점 O는 수중 글라이더 선체의 기하학적 중심으로 하였다. 또한 노즈콘 방향을 x_O축, 수심 방향을 z_O축으로 하여 오른손 좌표계를 이용해 수중 글라이더의 진행방향의 우현을 y_O축으로 설정하였다.

Figure 2:

Coordinate systems of underwater glider

3.2 수중 글라이더 모델링

설정한 좌표계에서 수중 글라이더의 운동을 나타내기 위한 운동방정식은 식 (1)과 같다. 식 (1)은 뉴턴-오일러에 의해 유도된 병진운동과 회전운동을 나타내는 좌항과 외력을 나타내는 우항으로 구성되어 있다[6].

$\[ \begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{m}_t\left[\dot{u}-vr+wq-x_G\left(q^2+r^2\right)+y_G\left(pq-\dot{r}\right)+z_G\left(pr+\dot{q}\right)\right]=X\hfill \\ m_t\left[\dot{v}-wp+ur-y_G\left(r^2+p^2\right)+z_G\left(pr-\dot{p}\right)+x_G\left(pq+\dot{r}\right)\right]=Y\hfill \end{array}\hfill \\ m_t\left[\dot{w}-uq+vp-z_G\left(p^2+q^2\right)+x_G\left(pr-\dot{q}\right)+y_G\left(qr+\dot{p}\right)\right]=Z\hfill \end{array}\hfill \\ I_{xx}\dot{p}+\left(I_{zz}-I_{yy}\right)qr-I_{yz}\left(q^2-r^2\right)+I_{xy}\left(pr-\dot{q}\right)-I_{zx}\left(pq+\dot{r}\right)+m\left[y_G\left(\dot{w}-uq+vp\right)-z_G\left(\dot{v}-wp+ur\right)\right]=K\hfill \end{array}\hfill \\ I_{yy}\dot{q}+\left(I_{xx}-I_{zz}\right)pr-I_{zx}\left(r^2-p^2\right)+I_{yz}\left(pq-\dot{r}\right)-I_{zy}\left(qr+\dot{p}\right)+m\left[z_G\left(\dot{u}-ur+wq\right)-x_G\left(\dot{w}-uq+vp\right)\right]=M\hfill \end{array}\hfill \\ I_{zz}\dot{r}+\left(I_{yy}-I_{xx}\right)pq-I_{xy}\left(p^2-q^2\right)+I_{zx}\left(qr-\dot{p}\right)-I_{yz}\left(pr+\dot{q}\right)+m\left[x_G\left(\dot{v}-wp+ur\right)-y_G\left(\dot{u}-ur+wq\right)\right]=N\hfill \end{array} \]$

(1)

위 식에서 m_t는 수중 글라이더의 총질량이며 다음과 같이 나타낼 수 있다.

$\[ m_t=m_s+m_h+m_m \]$

(2)

m_s는 수중 글라이더 내부 이동질량을 제외한 내부구성품의 질량, m_h는 수중 글라이더의 외부 선체의 질량, m_m은 내부 이동질량의 질량이다. u,v,w와 p,q,r은 선체고정좌표계의 각축의 병진운동과 회전운동의 속도와 각속도를 나타낸다. I_ij는 선체고정좌표계 각축의 수중 글라이더의 질량관성 모멘트를 나타낸다. 우변의 X,Y,Z와 K,M,N은 수중 글라이더에 작용하는 외력을 나타내며 부력, 중력, 유체력이 포함되어 있다. 외력에 포함된 유체력은 CFD해석, PMM시험, 경험식을 이용해 추정된 유체력 계수와 운동체의 속도에 의해 결정된다.

수중 글라이더는 부력엔진과 자세제어기에 운동에 의해 각각 부력중심, 질량중심과 질량관성모멘트가 실시간으로 변화가 생기며 이는 식 (1)에서 x_B,y_B,z_B의 변화, x_G,x_G,x_G변화와 I_ij의 변화로 표현된다.

부력중심과 질량중심, 질량관성모멘트는 수중 글라이더의 부력엔진과 자세제어기의 운동에 의해 실시간으로 변화하게 된다. 부력엔진 피스톤과 자세제어기 내부 이동질량의 이동속도가 수중 글라이더의 운동에 동역학적 영향을 줄 만큼 빠르지 않으므로 부력엔진 피스톤과 자세제어기 내부 이동질량의 동역학적 영향은 무시하여 기구학적 변화만 고려하였다.

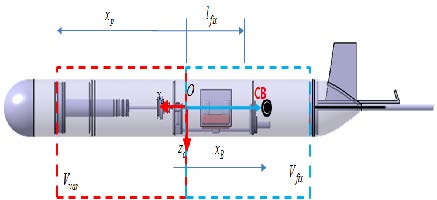
부력엔진 피스톤의 이동에 따라 수중 글라이더의 총 체적이 변화하게 된다. 실시간으로 변화하는 피스톤의 위치를 고려하기 위해 Figure 3에 변수를 나타내었다. 이를 이용하여 부력중심의 변화를 식으로 나타내면 식(3)과 같다.

Figure 3:

Position of the center of buoyancy

$\[ r_{cb}\left(t\right)={\left[x_B,\mathrm{0,0}\right]}^T=\left[\begin{array}{c}\frac{V_{var}\frac{x_p\left(t\right)}{2}+V_{fix}{l}_{fix}}{V_{var}+V_{fix}}\\ 0\\ 0\end{array}\right] \]$

(3)

위 식에서 V_fix는 선체고정좌표계의 원점에서 카울링 까지의 고정체적, V_var는 부력엔진 피스톤까지의 변화체적으로 나타내었다. x_p는 선체고정좌표계의 원점에서 피스톤까지의 거리를 나타내는 벡터이다.

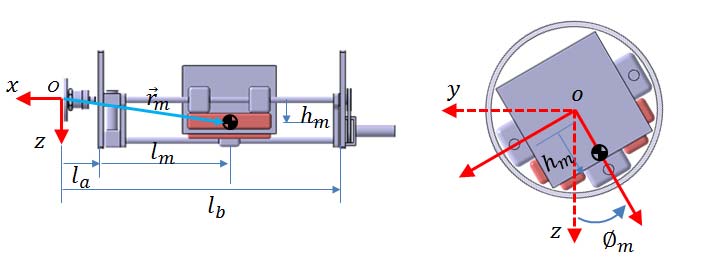
자세제어기 내부 이동질량의 위치변화에 따른 질량중심과 질량관성모멘트의 변화가 발생하게 된다. 이를 고려하기위해 Figure 4와 같이 변수를 설정하였다. 선체고정좌표계의 원점에서 내부이동 질량의 질량중심까지의 위치벡터 변화를 고려하여 수중 글라이더의 질량중심과 질량관성모멘트의 변화를 나타낼 수 있으며 질량중심의 변화는 식 (4)와 같이 나타낼 수 있다.

Figure 4:

Position of the inner moving mass

$\[ \begin{array}{c}{r}_m\left(t\right)={\left[x_m,y_m,z_m\right]}^T=\left[\begin{array}{c}{l}_a+l_m\\ -h_m\sin {\Phi }_m\\ h_m\cos {\Phi }_m\end{array}\right]\\ r_{CG}=\left[\begin{array}{c}{x}_G\\ y_G\\ z_G\end{array}\right]=\frac{m_{hull}{r}_h+m_{star}{r}_s+m_m{r}_m\left(t\right)}{m_t}\end{array} \]$

(4)

위의 식에서 r_m은 선체고정좌표계의 원점에서 내부 이동질량까지의 위치벡터, r_h는 선체 외부질량의 질량중심까지의 위치벡터, r_s는 내부구성품의 질량중심까지의 위치벡터이다.

또한 질량관성모멘트의 변화는 다음 식 (5)와 같이 나타낼수 있다.

$\[ I=\left(I_{hull}-m_{hull}\widehat{r_h}\widehat{r_h}\right)+\left(I_s-m_s\widehat{r_s}\widehat{r_s}\right)+\left(I_m-I_m\widehat{r_m}\left(t\right)\widehat{r_m}\left(t\right)\right) \]$

(5)

위의 식에서 I_hull은 선체고정좌표계의 원점에서 선체 외부질량의 질량관성모멘트, I_s는 내부구성품의 질량관성모멘트, I_m은 내부 이동질량의 질량관성 모멘트이며 연산자 ^은 왜대칭행렬(skew symmetric matrix)을 나타낸다[7].

3.3 부력엔진 모델링

앞선 절에서 유도한 부력엔진 피스톤의 위치변화는 시간에 따라 실시간으로 변화하게 된다. 수중 글라이더의 응답특성을 고려하기 위해서는 피스톤의 이동속도를 모델링 하여야 한다.

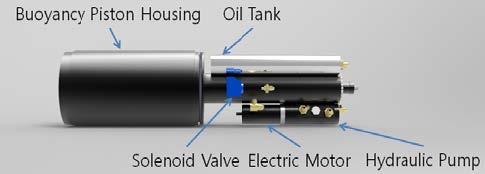
부력엔진의 외형은 Figure 5와 같으며 외부에 노출되는 피스톤 하우징과 유압탱크, 솔레노이드 밸브, 유압펌프, 유압펌프 모터로 구성되어 있다.

부력엔진의 피스톤이 선수방향으로 이동시에는 유압펌프를 구동해 유압유를 토출시켜 피스톤을 이동시키게 된다. 펌프에서 토출되는 유압유의 유량을 식으로 나타내면 식 (6)과 같다.

Figure 5:

Configuration of the buoyancy engine

$\[ q=D\bullet w_b-K_{leak}\bullet P \]$

(6)

위식에서 q는 유량, w_b는 유압펌프 모터 각속도, P는 유압펌프의 유입압력과 토출압력의 차이, K_leak는 누출계수이며 누출 계수는 다음과 같이 식 (7)로 나타낼 수 있다.

$\[ K_{leak}=\frac{K_{HP}}{\mu } \]$

(7)

K_HP는 Hagen-Poiseuille 계수이며 µ는 유체동점성이다. 유압펌프의 유입압력과 토출압력의 차이가 선형적으로 변화한다고 가정하면 Hagen-Poiseuille식을 이용하여 압력차이 P는 다음과 같은 식 (8)로 나타낼 수 있다.

$\[ P=\frac{\mu }{K_{HP}}{q}_{leak} \]$

(8)

위식에서 q_leak은 누출 유량으로써 다음과 같이 식 (9)로 나타낼 수 있다.

$\[ q_{leak}=D\bullet w_{bnom}\left(1-{\eta }_v\right) \]$

(9)

위식에서 D는 유압펌프 토출량, w_bnom은 유압펌프 모터의 공칭각속도, η_v은 유압펌프의 체적계수이다.

위의 식 (6) ~ 식 (9)를 정리하여 펌프 유량을 펌프 토출량과 유압펌프 모터의 각속도에 관한 식으로 정리하면 식 (10)과 같다.

$\[ q=D\bullet w_b-D\bullet W_{bnom}\left(1-{\eta }_v\right) \]$

(10)

위의 식을 이용하여 부력엔진의 유압펌프와 피스톤 이동속도의 관계식을 다음과 같이 식 (11)로 나타낼 수 있다.

$\[ v_b=\frac{D\bullet w_b-D\bullet w_{bnom}\left(1-{\eta }_v\right)}{A} \]$

(11)

위 식에서 v_b는 부력엔진 피스톤의 이동속도, A는 피스톤의 면적이다.

수중 글라이더의 에너지 효율을 높이기 위하여 부력엔진 피스톤을 후진 시에는 솔레노이드 밸브를 개방시켜 외부의 압력과 피스톤 하우징 내부의 압력차에 의해 피스톤이 후진하게 되도록 설계하였으며, 후진 시 피스톤 이동속도는 실제 부력엔진의 하우징에 외압을 인가하여 실험을 통해 얻은 데이터를 바탕으로 근사화된 식을 이용하였다.

3.4 자세제어기 모델링

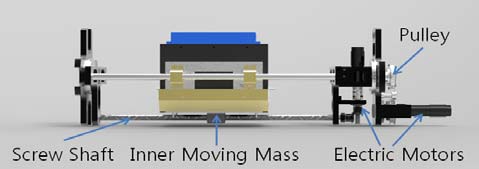
수중 글라이더의 자세제어기는 Figure 6과 같다. 수중 글라이더는 외부의 방향타나 비대칭적 추진력을 이용한 방향전환, 자세제어가 아닌 내부 이동질량의 위치변화를 이용하여 자세를 제어하게 된다. 자세제어기 내부 이동질량은 병진운동과 회전운동이 가능하게 설계 되어 있다.

Figure 6:

Configuration of the motion controller

병진운동을 제어하기 위하여 하나의 전동모터와 스크류 샤프트를 이용하며 전동모터의 각속도와 스크류 샤프트의 리드 길이에 의해 내부 이동질량 병진운동의 이동속도가 결정된다.

회전운동은 전동모터와 풀리를 이용하여 회전운동이 가능하도록 기구부 구성이 되어 있으며 내부 이동질량의 회전운동시 회전속도는 전동모터의 각속도에 의해 결정되게 된다.

수중 글라이더의 자세제어기 모델링을 수행하기 위하여 자세제어기에 사용되는 전동모터의 모델링을 수행하였으며 식(12)와 같이 나타낼 수 있다.

$\[ \begin{array}{c}\frac{d^2\theta }{{dt}^2}=\frac{1}{J}\left(K_{t}i-b\frac{d\theta }{dt}\right)\hfill \\ \frac{di}{dt}=\frac{1}{L}\left(-Ri+V-K_e\frac{d\theta }{dt}\right)\hfill \end{array} \]$

(12)

위의 식에서 J는 로터의 질량관성모멘트, K_t는 모터 토크 계수, K_e는 역기전력 상수, b는 모터 점성마찰 계수, R은 전기저항, L은 인덕턴스 θ는 로터의 각도이다.

식 (12)에서 계산된 전동모터의 각속도를 이용하여 내부 이동질량의 병진운동을 나타내면 식 (13)과 같다.

$\[ v_m={\eta }_g\bullet w_m\bullet L_m \]$

(13)

v_m은 내부 이동질량의 이동속도, η_g 감속기의 기어비, w_m는 전동모터의 각속도, L_m은 스크류 샤프트의 리드길이를 나타낸다.

4. 운동특성 해석

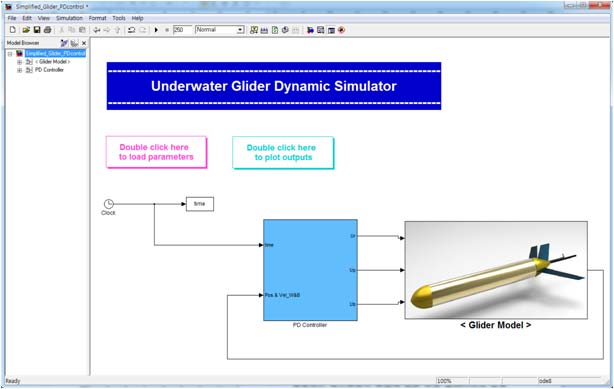
부력엔진과 자세제어기의 운동에 따른 수중 글라이더의 운동특성을 해석하기 위해 수중 글라이더의 6자유도 비선형 운동방정식에 부력엔진과 자세제어기의 모델링을 적용하여 수중 글라이더의 응답특성을 고려한 시뮬레이터를 Matlab/Simulink를 이용하여 개발하였다. Figure 7은 개발된 시뮬레이터를 나타낸다. 수중 글라이더 그림블록은 글라이더의 수학적 모델링을 포함하고 있으며, 그림블록 좌측의 파란 블록은 PID 컨트롤러와 자세제어기, 부력엔진의 전동모터와 피스톤의 수학적 모델링을 포함하는 블록이다. 수중 글라이더 운동방정식에서 계산한 출력값을 PID 컨트롤러에 피드백 시키는 구조를 가지고 있다.

Figure 7:

Underwater glider dynamic simulator

운동 시뮬레이션에서 사용된 유쳬력 계수는 PMM시험을 이용하여 추정한 선형 유체력 계수[8]와 경험식을 이용하여 추정한 비선형 유체력 계수[9]를 사용하였으며 운동 시뮬레이션은 조류와 외란이 없는 상태로 수행하였다.

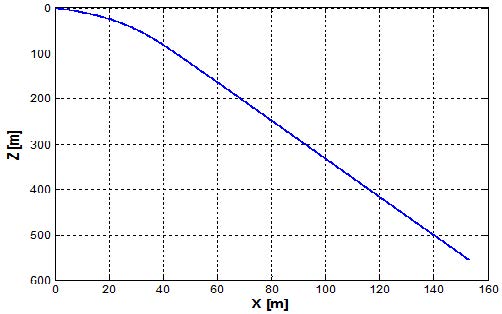
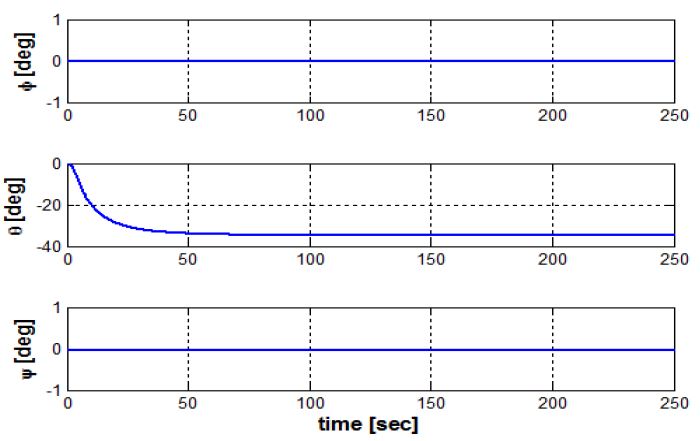
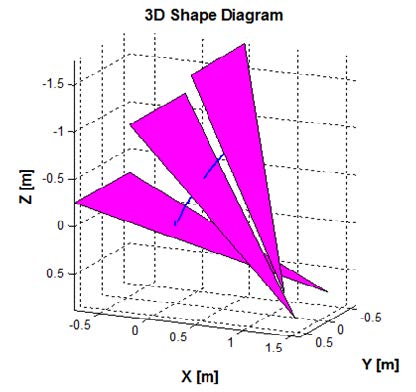
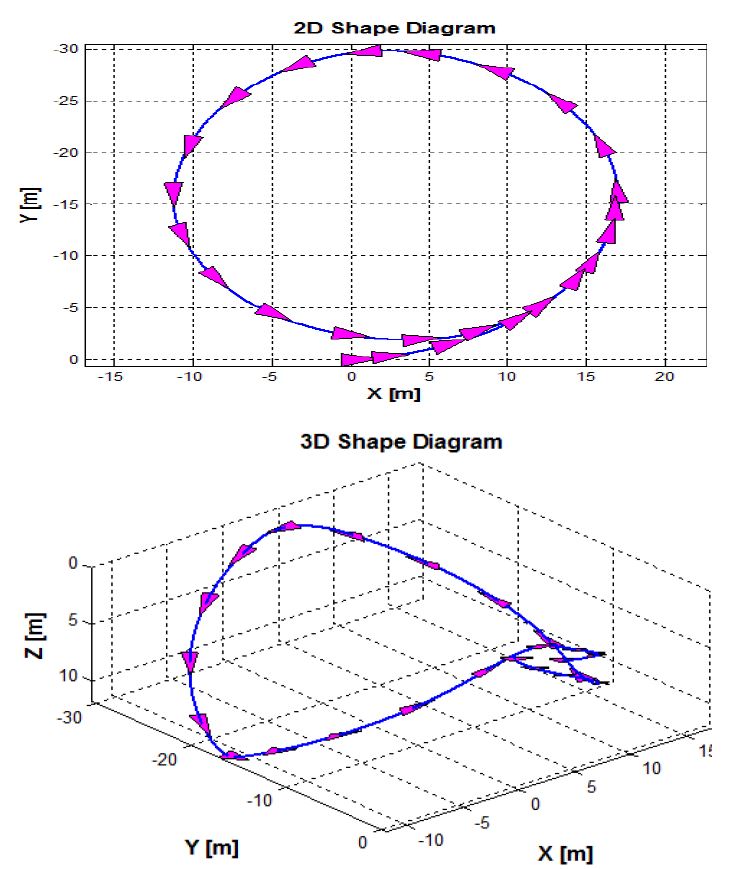
부력엔진 피스톤위치 변화에 따른 수중 글라이더의 운동특성을 확인하기 위해 부력엔진 피스톤의 위치를 후진할 수 있는 최대치로 후진시켜 시뮬레이션을 수행하였다. Figure 8은 부력엔진에 의해 발생하는 수중 글라이더의 수직면 운동을 나타내었으며 피스톤이 후진하여 부력이 중력보다 작게 되어 수중 글라이더가 잠항하는 것을 확인할 수 있다. 이때의 자세의 변화는 Figure 9와 같으며 부력중심의 변화로 인해 종동요각이 발생하는 것을 확인할 수 있다. 또한 자세제어기 내부 이동질량의 위치변화에 따른 수중 글라이더의 운동특성 역시 수중 글라이더의 중요한 요소 이다. 자세제어기에 의해 발생되는 회전운동 확인을 위해 부력엔진 피스톤을 피스톤 하우징 중심에 두고 자세제어기 내부 이동질량의 위치를 최대로 전진시켰다. 이때의 3차원 자세 그래프는 Figure 10과 같으며 각도의 변화는 Figure 11과 같다. 3차원 자세 그래프에서 삼각형의 가장 뾰족한 부분이 수중 글라이더의 선수 방향이며 그래프에서 선미가 수면으로 노출되는 것을 확인할 수 있다.

Figure 8:

2D Trajectory of underwater glider

Figure 9:

Angles of underwater glider

Figure 10:

3D attitude diagram of underwater glider

Figure 11:

Angles of underwater glider when moving mass moves forward

이때의 종동요각은 약 -78°이다. 이는 이미 상용화된 글라이더 들이 외부와 통신을 하기위해 수면에서 취하는 자세와 동일하며 자세제어기만을 사용하여 외부통신자세가 가능함과 자세제어기에 의해 회전운동이 발생되는 것을 확인하였다.

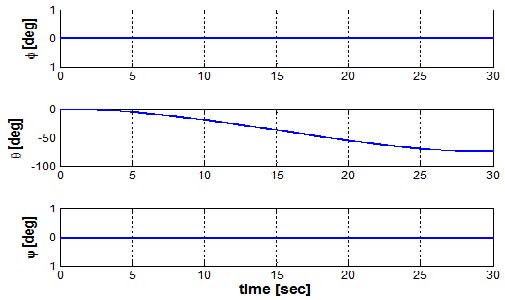
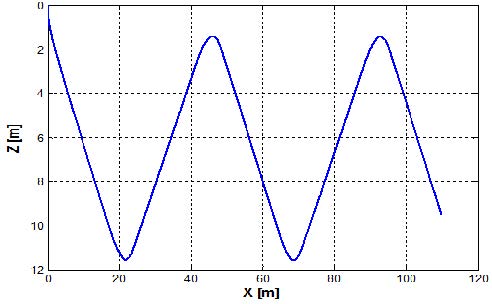
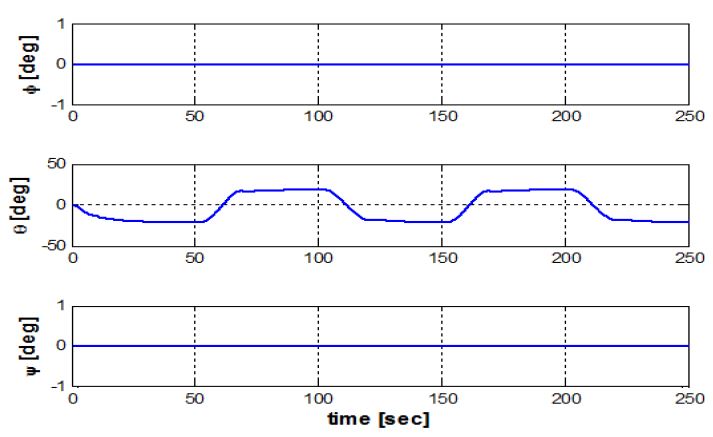
수중 글라이더의 운용목적은 에너지 효율의 극대화 이므로 수중 글라이더 운용 시 가장 에너지 소모가 큰 부력엔진의 운용을 최소화 하여야 한다. 상승 최소수심과 하강 최대수심을 두고 x_E방향으로 같은 거리 만큼 이동시 부력엔진의 운용을 최소화하기 위해선 상승과 하강 횟수를 최소화 하여야 한다. 상승과 하강 횟수의 최소화는 특정 종동요각을 수중 글라이더가 가짐으로써 가능하게 되며 이를 위해 운동 시뮬레이션에서는 PID제어기를 사용하여 자세제어기 내부 이동질량의 위치를 제어하여 특정 종동요각을 가지도록 하였다. PID제어기의 이득값은 운동 시뮬레이션 결과를 통한 경험적 방법으로 튜닝을 하였으며 비례항 이득값 10, 적분항 이득값은 3, 미분항 이득값을 20으로 하였다. 수중 글라이더는 물리적으로 제어기의 제어값에 의해 즉각적으로 운동이 변화 하지 않으므로 비례항의 이득보다 미분항의 이득을 크게 두어 오버슛을 줄이고 안정성을 향상할수 있도록 하였다. Figure 12와 같은 수직평면 운동을 할 때 목표 종동요각이 하강시 -20°, 상승시 20°가 되도록 제어를 하였으며 이때 각도의 변화는 Figure 13과 같으며 종동요각이 목표값을 추종하는 것을 확인할 수 있다.

Figure 12:

2D trajectory of pitch control

Figure 13:

Angles of underwater glider under pitch control

Figure 12에서의 상승 최소 수심은 3m, 하강 최대 수심은 10m로 하였으나 목표 수심을 벗어나는 것을 확인할 수 있다. 이는 부력엔진 피스톤의 이동속도가 느려 부력 또한 느리게 변화하기 때문으로 예상되며 하강 수심범위를 넘을 시 해저면과 충돌 가능성이 있기 때문에 운용 알고리즘으로의 보완 필요성이 있다.

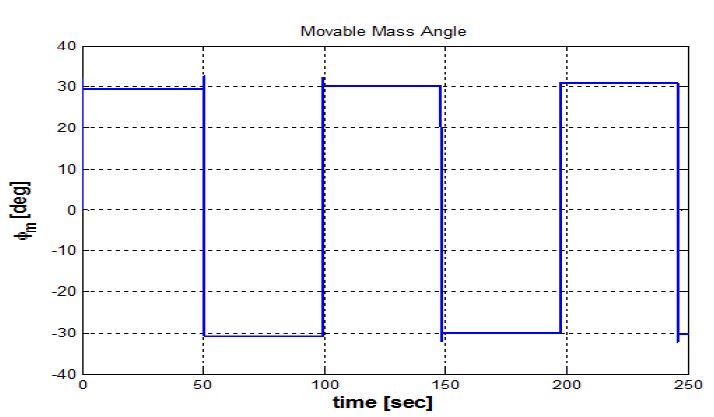
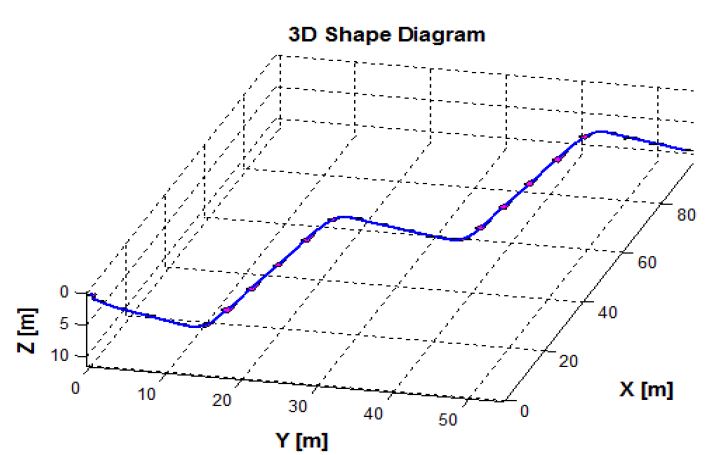
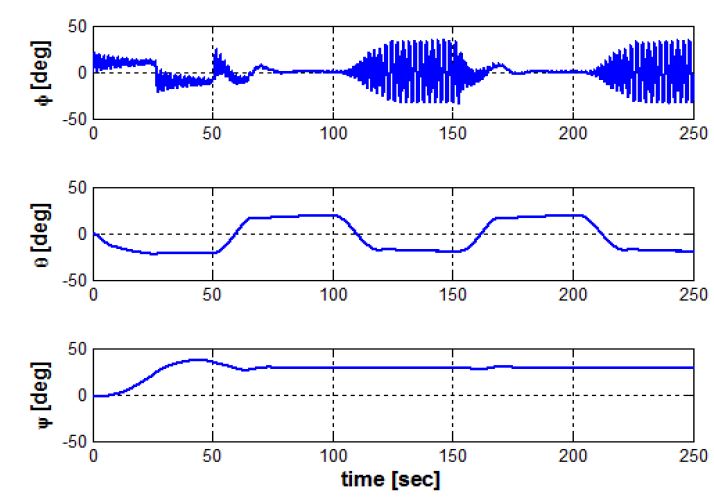
수중 글라이더의 방향을 제어하기 위해서는 자세제어기 내부 이동질량을 회전시켜야 한다. Figure 14와 같이 내부 이동질량의 회전을 이용한 선회가 가능하며 종동요각 제어와 같은 조건에서 선회하면 회전반경이 약 13m가 되는 것을 확인할 수 있다. 이때 Figure 15에서 보이는 바와 같이 내부 이동질량의 회전각도는 하강시 30°, 상승시 -30°가 되도록 하였으며 상승과 하강시에 회전각도가 대칭적으로 변해야 선회가 가능함을 보이고 있다. 수중 글라이더가 상승 하강 운동을 하면서 원하는 목표점까지 이동하기 위해서는 방향각 제어가 필수적이다. 이를 위해 선회운동 시뮬레이션 결과를 바탕으로 수평면의 선수동요각 제어를 수행하였다. 방향각제어 운동 시뮬레이션은 종동요각제어 운동 시뮬레이션과 같은 조건에서 목표 선수동요각을 추종 할 수 있도록 하였으며 3차원 궤적은 Figure 16과 같고 이때의 각도는 Figure 17과 같다. Figure 17에서 확인할 수 있듯 선수동요 값을 추종하는 것을 확인 할 수 있다.

위와 같이 운동 시뮬레이션을 이용하여 수중 글라이더의 운동특성을 해석하였으며, 운동특성을 반영한 동역학 모델링의 유효성을 정성적으로 확인할 수 있었다. 추후 실해역실험을 통한 동역학 모델의 타당성을 검증할 계획이다.

Figure 14:

Tuning simulation of underwater glider

Figure 15:

Rotation of inner moving mass

Figure 16:

3D trajectory of underwater glide under heading control

Figure 17:

Angles of underwater glider under heading control

5. 결 론

본 논문에서는 수중 글라이더의 운동특성을 반영한 동역학 모델링을 수행하였고, 전개된 운동방정식을 이용하여 시뮬레이션 프로그램을 구성하였으며, 운동 시뮬레이션 결과를 통하여 모델링의 유효성을 정성적으로 확인할 수 있었다. 수중 글라이더의 운용목적인 에너지 효율 극대화를 위한 종동요각 제어를 수행하여 자세제어기를 이용한 종동요각 제어가 가능함을 확인하였으며, 또한 자율운항이 가능하기 위한 방향각제어가 자세제어기의 회전에 의해 가능함을 운동 시뮬레이션을 통해 확인할 수 있었다. 추후 실해역 실험을 통해 수중 글라이더 동역학 모델링의 타당성을 검증하고 느린 응답 특성을 가지는 시스템을 제어하기위한 제어 알고리즘을 적용하는 연구를 추진할 계획이다.

Acknowledgments

본 논문은 해양수산부 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구임(해양개발용 수중건설로봇사업단, PJT200539)

References

• D. C. Webb, P. J. Simonetti, and C. P. Jones, “SLOCUM, an underwater glider propelled by environmental energy”, IEEE Journal of Oceanic Engineering, 26(4), p437-446, (2001). [https://doi.org/10.1109/48.972077]
• C. C. Eriksen, T. J. Osse, R. D. Light, T. W. Lehman, P. L. Sabin, J. W. Ballard, and A. M. chiodi, “Seaglider; A long-range autonomous underwater vehicle for Oceanographic research”, IEEE Journal of Oceanic Engineering, 26(4), p424-436, (2004). [https://doi.org/10.1109/48.972073]
• D. L. Rudnick, R. E. Davis, C. C. Eriksen, D. M. Fratantoni, and M. J. Perry, “Underwater gliders for ocean research”, Marine Technology Society Journal, 38(2), p73-84, (2004). [https://doi.org/10.4031/002533204787522703]
• J. Sherman, R. Davis, W. B. Owens, and J. Valdes, “The autonomous underwater glider Spray”, IEEE Journal of Oceanic Engineering, 26(4), p437-466, (2001). [https://doi.org/10.1109/48.972076]
• D. F. Myring, “A theoretical study of body drag in subcritical axisymmetric flow”, Aeronautical Quarterly, p186-194, (1976).
• T. L. Fossen, Guidance and Control of Ocean Vehicles, NY, USA: John Wiley & Sons Inc, (1994).
• J. G. Graver, Underwater Gliders; Dynamics, Control and Design, Ph.D. Dissertation, Department of Mechanical and Aerospace Engineering, Princeton University, USA, (2005).
• J. W. Jung, J. H. Jeong, I. G. Kim, and S. K. Lee, “Experimental study on hydrodynamic coefficients of autonomous underwater glider using vertical planar motion mechanism test”, Journal of Ocean Engineering and Technology, 28(2), p119-125, (2014). [https://doi.org/10.5574/KSOE.2014.28.2.119]
• T. J. Prestero, Verification of a Six-Degree of Freedom Simulation Model for the REMUS Autonomous Underwater Vehicle, M.S Thesis, Department of Ocean Engineering, Massachusetts Institute of Technology/Woods Hole Oceanographic Institution, USA, (2001).