2상 마이크로 채널 히트 싱크에서의 유동 비등 열전달에 관한 연구
© 2015 Korean Society of Women Health Nursing
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 FC-72를 작동 유체로 사용하여 이상 유동 비등에 관한 실험을 수행하였다. 마이크로 채널은 깊이 0.2mm, 폭 0.45mm, 길이 60mm 그리고 채널의 개수는 15개로 구성되었다. 실험은 질량유속과 열유속 각각 200-400 kg/m2s, 5.6-49.0 kW/m2 범위와 증기 건도 0.02-0.93 범위에서 수행되었다. 실험 결과에 따르면 낮은 건도(x < 0.2)영역에서는 핵비등에 의한 열전달이 지배적으로 작용하며, 그 이상의 증기 건도 영역에서는 핵비등과 강제 대류 비등의 영향이 복합적으로 작용하는 것으로 나타났다. 핵비등과 강제 대류 비등은 각각 비등수와 대류수에 관한 함수로 표현할 수 있으며, 실험에서 얻어진 열전달 계수는 기존의 상관식에 의한 열전달 계수와 비교하였다.
Abstract
Two-phase flow boiling experiments were conducted using FC-72 as the working fluid. The micro-channels consisted of 15 channels with a depth of 0.2 mm, width of 0.45 mm, and length of 60 mm. Tests were performed over a mass flux range of 200–400 kg/m2s, heat flux range of 5.6–49.0 kW/m2, and vapor quality range of 0.02–0.93. Based on the results of the experiment, the heat transfer mechanism by nucleate boiling was dominant at a lower vapor quality (x < 0.2), whereas that in the region of a vapor quality greater than 0.2 was complexly influenced by nucleate boiling and forced convection boiling. The nucleate boiling and forced convection boiling could be expressed as functions of the boiling number and convection number, respectively. In addition, the heat transfer coefficient obtained by the experiment was compared with the heat transfer coefficient by the existing correlation.
Keywords:
Boiling number, Convection number, Heat transfer, Micro channels, Two-phase flow키워드:
비등수, 대류수, 열전달, 마이크로 채널, 이상 유동1. 서 론
마이크로 채널을 이용한 히트 싱크에 관한 연구는 Tuckerman et al. [1]가 초고 집적회로(VLSI : very large scale integrated circuit)의 냉각 성능 향상을 위해 제안한 이후 현재까지 활발하게 진행되고 있다. 특히, 전기·전자 분야에서는 18개월마다 마이크로 칩의 밀도가 2배로 증가한다는 무어의 법칙[2]을 따라서 집적회로의 성능은 꾸준히 증가하고 있다. 하지만 이로 인해서 단위 면적당 발생하는 열 또한 계속해서 증가하고 있으므로, 최근에는 이러한 발열을 효과적으로 제거하는 기술의 개발이 중요한 과제로 부각되고 있다.
전기·전자 분야 외 다양한 분야에서도 마이크로 채널을 이용한 히트싱크를 적용하여 높은 열소산 능력을 활용하고 있다. 가스 터빈 블레이드의 냉각[3], 로켓 엔진의 연소실 및 노즐 케이싱의 냉각[4] 그리고 수소 에너지 저장 시스템[5][6] 등이 그 예이다.
그리고 2상 유동 비등을 히트 싱크에 적용하게 되면 단상 유동에 비해서 높은 열전달 계수 값을 가지며, 이때 작동유체가 흡수하는 열은 대부분 상변화에 요구되는 잠열에 사용되므로 단상 유동에 비해서 시스템 내부의 온도 분포를 작동유체의 포화온도 부근에서 비교적 일정하게 유지할 수 있다.
마이크로 채널을 이용한 히트 싱크를 효과적으로 적용하기 위해서는 비등 열전달 메커니즘을 파악하여 열전달 특성을 확인하는 것이 우선되어야 한다. 채널 유동 시 비등 열전달 메커니즘은 크게 핵비등과 강제 대류 비등에 의한 열전달로 구분된다[7].
Lazarek et al. [8]은 직경 3.15mm의 튜브에서 R-113을 작동유체 사용하여 비등 실험을 수행하였으며, 그 결과 핵비등을 2상 유동 비등에서의 주요 열전달 메커니즘으로 분석하였다.
Bao et al. [9]은 R11과 HCFC123을 작동 유체로 사용하여 1.95mm 직경의 튜브에서 비등 열전달 실험을 수행하였으며, Lazarek and Black과 마찬가지로 핵비등을 주요 열전달 메커니즘으로 보았다.
반면에 Lee et al. [10]는 R113을 작동 유체로 사용한 실험에서 열전달 계수는 대부분의 경우 열유속 보다는 질량유속과 증기 건도에 대한 영향을 많이 받는 것으로 나타났으며, 이에 따라서 강제 대류 비등에 의한 열전달이 주요 메커니즘으로 작용한다고 주장하였다.
Kandlikar [11]는 무차원 수인 대류수(convection number, Co) 에 따라서 다음과 같이 비등 열전달의 주요 메커니즘을 구분하였다.
CO < 0.65 - forced convective boiling
CO < 0.65 - nucleate boiling
Lee et al. [12]는 건도에 따라서 낮은 건도(x < 0.05)에서는 핵비등에 의한 열전달이 이루어지며, 중간 건도(0.05 < x < 0.55)와 높은 건도(x > 0.55)에서는 강제 대류 비등에 의한 열전달이 이루어진다고 보고하였다.
Megahed [13]는 본 연구와 동일한 작동 유체인 FC-72를 사용하여 비등 열전달 실험을 수행하였으며, Lee and Mudawar의 연구 결과와 유사하게 건도 변화에 따라서 비등 열전달의 주요 메커니즘이 달라진다고 보고하였다. Megahed는 낮은 건도(x < 0.2)에서는 핵비등에 의한 열전달, 0.2이상의 건도에서는 핵비등과 강제 대류 비등이 복합적으로 일어난다고 주장하였다.
본 연구에서는 전기·전자 분야에서 냉매로 주로 활용되는 FC-72를 작동 유체로 사용하여 마이크로 채널에서의 2상 유동 비등 열전달 실험을 수행하였으며, 마이크로 채널에서의 비등 열전달 특성 및 메커니즘을 분석하였다.
2. 실험장치 및 방법
2.1 실험 장치
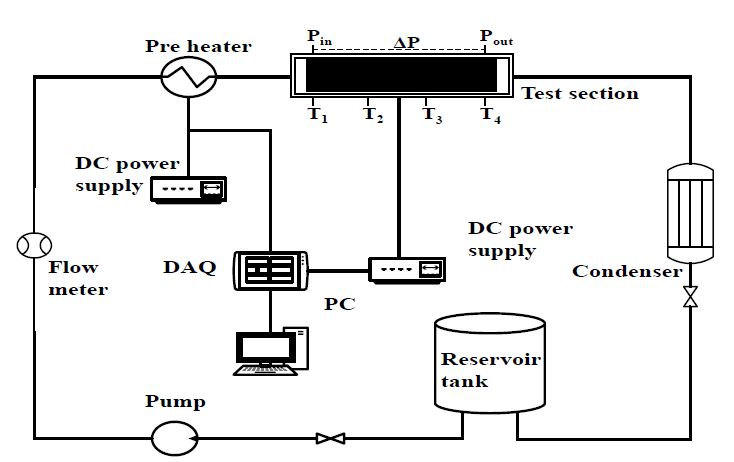
Figure 1은 본 연구에서 사용된 실험장치의 개략도를 나타내고 있으며, 저장탱크, 기어펌프, 유량계, 예열기 그리고 시험부로 이루어져 있다. 본 연구에서는 작동유체로 FC-72 냉매를 사용하였으며, 냉매의 흐름은 먼저 저장탱크에서 기어펌프를 통해 유량계를 거쳐 시험부로 유입된 후 저장탱크로 다시 모이는 폐회로 시스템으로 구성되어 있다.
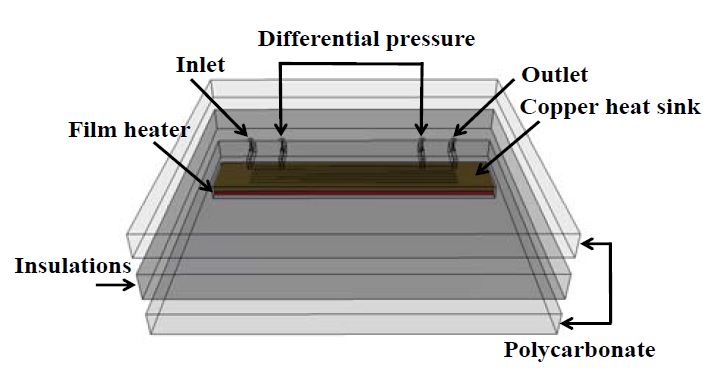
Figure 2는 시험부를 나타내며, 마이크로 채널의 깊이와 폭은 각각 0.2 mm, 0.45 mm이며, 채널수는 15개로 제작되었다. 채널의 총길이는 60 mm이며, 압력 측정은 40 mm에 이르는 구간에서 이루어졌다. 마이크로 채널에 일정한 열량을 공급해주기 위해 필름히터가 마이크로 채널이 있는 동판의 하부에 설치된다. 필름히터와 연결된 직류 전원 공급 장치는 0~50 V와 0~0.3 A의 전압과 전류 범위 내에서 조절되며, 필름히터에 인가되는 전압과 전류를 측정하여 시험부에 전달되는 열량을 계산하게 된다. 동판과 필름히터 사이에 T-type 열전대 4개를 부착하여 온도를 측정하며, 열손실을 최대한 방지하기 위해 단열재를 설치하였다. 또한 동판의 상부에는 채널의 유동을 직접 관찰할 수 있도록 폴리카보네이트로 제작한 투명한 커버를 부착하였다[14].
2.2 실험방법
먼저 실험을 시작하기 전에 시스템 내부의 용존 기체를 완전히 제거하기 위해 시스템 내부를 순환하는 작동유체를 예열기와 시험부의 필름히터를 통해 가열하여 증발시킴으로써 가스제거(degassing) 작업을 수행하였다.
실험이 진행되는 동안 작동유체의 유량은 유량계에 의해 측정되며, 본 연구에서 작동유체의 유량은 질량유속 200, 300 그리고 400 kg/m2s의 범위에서 수행되었으며, 각 질량유속에서 시험부에 가해진 열유속은 5.6 에서 49.0 kW/m2까지이다. 실험조건과 범위는 Table 1과 같다.
일정한 질량유속과 열유속에서 작동유체의 입구온도를 조절하여 출구 증기 건도를 조절한 이전 연구[15]와는 다르게 본 연구에서는 입구온도는 일정하게 고정한 채 열유속을 조절하여 출구 증기 건도를 조절하였다. 작동유체의 입·출구 온도는 T-type 열전대를 사용하여 측정하였으며, 압력강하는 차압계를 사용하여 측정하였다. 실험에서 측정된 값들은 데이터 수집 장치(data acquisition equipment)를 이용하여 수집 분석 하였다. 이때 데이터 수집 장치의 데이터 측정 간격은 0.5s 이다. 그리고 측정된 값들의 불확실성은 유량과 압력강하의 경우 각각 풀 스케일에서 ±3%, ±0.25%이다. 또한 온도 측정의 불확실성은 ±0.3℃이다[16]. 작동유체인 FC-72의 물성치는 제조사인 3M사에서 제공하는 자료를 이용하였다.
3. 결과 및 고찰
채널 내부에서 비등이 시작되면 채널 내부 벽면의 핵점에서 기포가 형성되고 열유속이 증가하면서 생성된 기포는 점차 성장하며, 일정한 크기가 되면 벽면에서 이탈하게 된다. 이어서 액체는 기포가 생성되어 이탈했던 핵점으로 유동하여 다시 핵점에서 기포가 형성된다. 즉, 기포의 생성, 이탈 그리고 액체의 유입에 의한 열전달이 주를 이루게 된다. 열유속을 더욱 증가시켜 건도를 더욱 증가시키게 되면 기포의 이탈과 재적심(rewet)이 충분히 이루어지면서 채널내부에는 이탈된 기포에 의한 기포류(bubbly flow)와 슬럭류(slug flow)가 형성된다. 특히, 마이크로 채널에서는 좁은 채널 직경으로 인해서 기포류와 슬럭류의 기포는 채널 벽면에 의해 압착되어 성장에 방해를 받게 된다. 압착된 증기 기포는 열유속의 증가와 함께 채널 벽면과 접하는 빈도가 증가하게 되며, 결국 열전달률은 감소하게 된다. 여기에서 열유속을 더욱 증가시키게 되면 기포는 서로 합쳐지는 과정을 거쳐 슬럭류에서 파형/환상류(wavy/annular flow)로 천이하게 된다. 파형/환상류에서는 채널 중심부에는 증기가 빠른 속도로 유동하며, 채널의 벽면에는 얇은 액막이 존재한다. 벽면을 통해 공급되는 열유속은 채널 벽면의 얇은 액막을 증발시켜 증기와 액막의 계면에서 열과 질량을 전달한다. 공급되는 열유속이 임계 열유속을 초과하게 되면 채널 내부의 액체는 대부분 증발하게 되며, 증기만의 유동인 드라이 아웃(dry-out)이 발생된다. 본 연구의 실험 범위는 과냉각 비등 영역에서 드라이 아웃 이전의 포화 비등 영역에 포함된다.
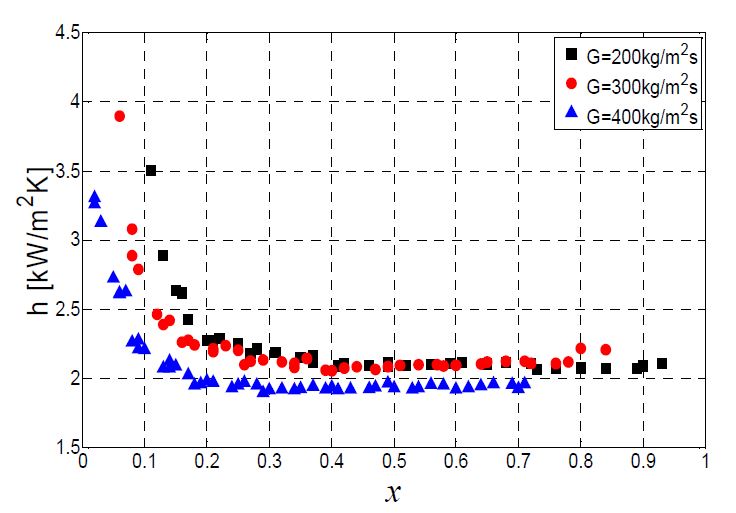
Figure 3은 각 질량 유속에서 증기 건도 변화에 따른 열전달 계수의 변화를 나타낸 것이다. 낮은 증기 건도에서는 즉, 기포류와 슬럭류의 형성이 이루어지는 지점에서는 증기 건도가 증가함에 따라서 열전달 계수는 급격하게 감소하였으며, 일정 건도 이상에서는 증기 건도와는 무관하게 비교적 일정한 값으로 유지되었다. 핵비등에 의한 열전달이 비등 열전달의 주요 메커니즘으로 작용하는 경우 채널 내부에서의 기포류와 슬럭류가 대부분의 영역을 차지하며, 이때 열전달 계수는 열유속에 강하게 의존하며, 증기 건도와 질량 유속에는 크게 영향을 받지 않는 것으로 알려져 있다. 반면에 강제 대류 비등에 의한 열전달이 비등 열전달의 주요 메커니즘으로 작용할 때에는 전자와 비교해서 기포류와 슬럭류에서 파형/환상류로의 천이가 일찍 발생하여 채널 내부를 대부분 파형/환상류 영역이 차지하게 된다. 이때의 열전달 계수는 열유속 보다는 증기 건도와 질량 유속에 주로 의존한다.
급격하게 열전달 계수가 감소하는 영역에서는 핵비등의 영향이 지배적이라고 볼 수 있으며, 이후에 열전달 계수가 더 이상 감소하지 않고 거의 일정하게 유지되는 것은 핵비등 외에도 강제 대류 비등의 영향이 나타나는 것으로 간주할 수 있다.
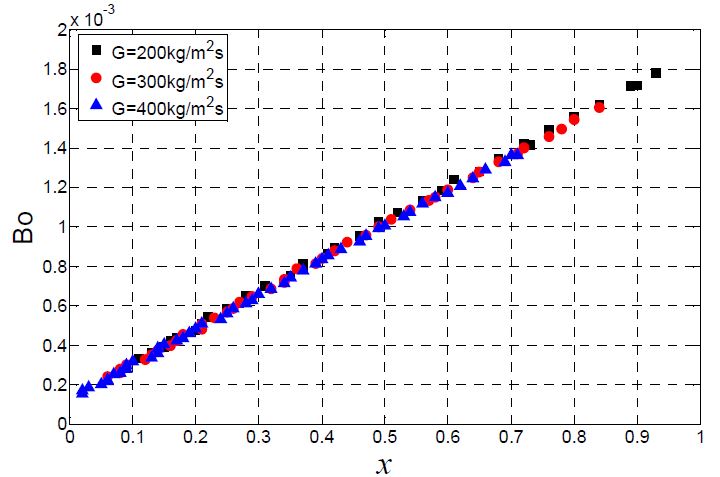
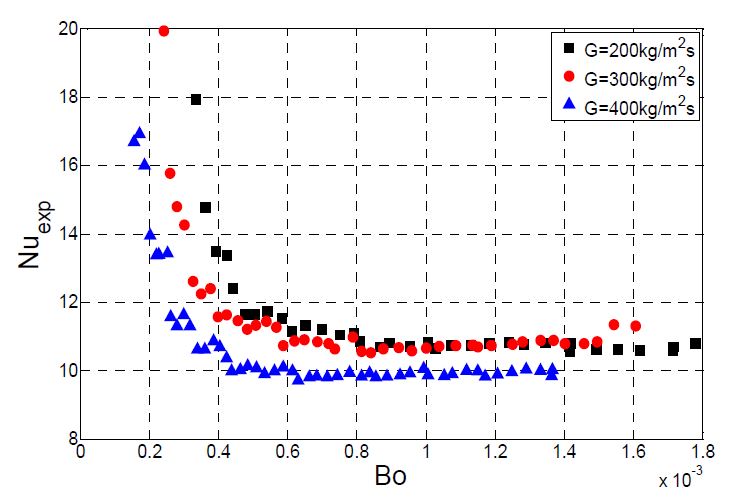
Figure 4와 5는 비등수(boilng number, Bo)와 증기 건도, 너셀수(Nusselt number, Nu)와의 관계를 나타내었다. 비등수는 식 (1)과 같이 정의된다.
| (1) |
여기서 q″는 열유속을 의미하며, G와 hlv는 각각 질량 유속과 잠열을 나타낸다.
비등수는 Figure 4와 같이 증기 건도에 일차 비례하며, Figure 5에 나타낸 것과 같이 비등수가 증가할수록 너셀수는 감소하였다. 그리고 비등수 변화에 대한 너셀수의 변화는 증기 건도 변화에 따른 열전달 계수의 변화 경향과 유사하게 나타났다. 높은 증기 건도(x > 0.2), 즉 높은 비등수(Bo > 0.5) 에서는 비등수가 열전달에 미치는 영향이 감소하는 것으로 볼 수 있다.
비등 열전달 계수를 예측하는 기존의 상관식을 살펴보면 Shah [17], Kandlikar [11] 그리고 Warrier et al. [18]은 비등 열전달 계수를 비등수에 관한 함수로서 상관식을 정의하였다. Warrier et al.은 열전달 계수를 비등수만의 함수로 정의한 것에 반해서 Shah와 Kandlikar는 핵비등 요소와 강제 대류 비등 요소를 사용해서 두 요소 중에 큰 값을 취하는 상관식을 각각 식 (2)와 식 (3)과 같이 제안하였다. 즉, 핵비등과 강제 대류 비등 메커니즘 중 더 강하게 나타나는 메커니즘에 의한 열전달이 이루어지는 것으로 나타내었다.
| (2) |
여기서 하첨자 tp와 sp는 각각 two-phase와 single-phase를 의미하며, Dh는 수력직경을 뜻한다. 그리고 E와 S는 각각 핵비등 요소와 강제 대류 비등 요소를 나타낸다.
| (3) |
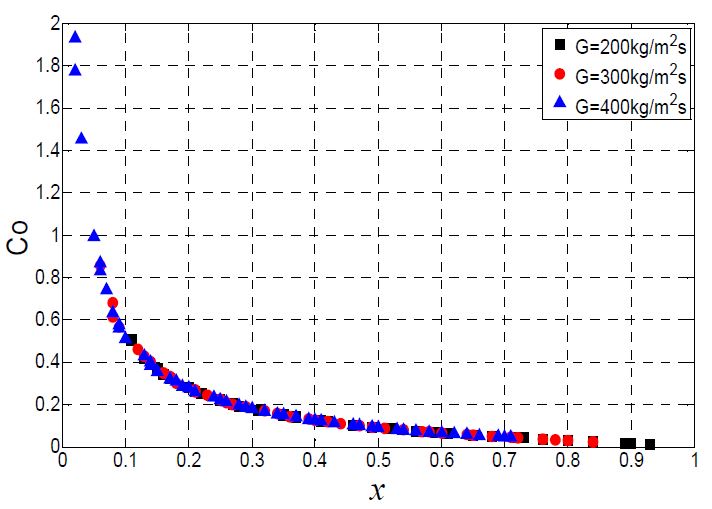
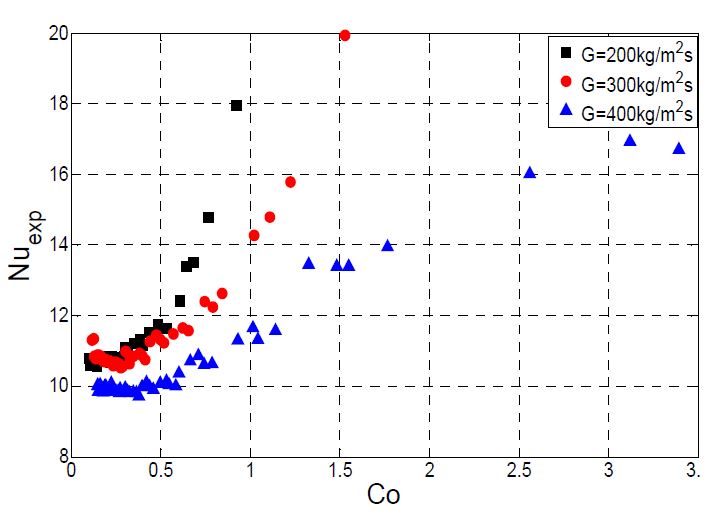
Figure 6 과 7은 대류수(convection number, Co)와 증기 건도, 너셀수(Nusselt number, Nu)와의 관계를 나타내었다. 대류수는 식 (4)와 같이 정의된다.
| (4) |
대류수는 식 (5)와 같이 정의되는 Martinelli 변수와 유사하며, Martinelli 변수에서 점성 항이 제거된 형태로 나타난다.
| (5) |
Figure 6에서 나타낸 것과 같이 대류수는 증기 건도와 반비례하며, Figure 7과 같이 대류수가 증가할수록 너셀수 또한 증가하였다. Shah의 상관식 식 (2)에서 강제 대류 비등 요소를 대류의 함수로 나타내었으며, Kandlikar의 상관식인 식 (3)을 보면 강제 대류 비등 요소에서는 핵비등 요소와 비교해서 대류수의 지수의 절대 값이 증가하였다. 즉, 강제 대류 비등에서는 대류수가 열전달에 미치는 영향이 증가하는 것으로 볼 수 있다.
본 연구의 실험 결과에 따르면 낮은 증기 건도(x < 0.2) 영역에서는 핵비등의 영향이 지배적이며, 증기 건도가 증가할수록 핵비등의 영향이 감소하며, 동시에 강제 대류 비등의 영향이 증가하는 것으로 판단할 수 있다. 이때 핵비등과 강제 대류 비등은 각각 비등수와 대류수에 관한 함수로서 나타낼 수 있다.
Kim et al. [19]는 Churchill et al. [20]의 방법을 이용하여 식 (6)과 같이 열전달 계수를 핵비등과 강제 대류 비등의 영향을 동시에 포함시키는 식으로 표현하였다. Shah와 Kandlikar의 상관식들과 유사하게 Kim and Mudawar 역시 핵비등을 비등수의 함수로서 나타내었으며, 강제 대류 비등에서는 비등수의 비중을 감소시키면서 대류수와 유사한 Martinelli 변수에 관한 항을 추가하였다.
| (6) |
여기서 하첨자 nb와 cb는 각각 nucleate boiling(핵비등)과 forced convection boiling(강제 대류 비등)을 의미한다. 그리고 PH 와 PF는 각각 채널의 접수둘레와 가열둘레를 나타내며, PR은 환산압력(P/Pcritical)을 나타낸다.
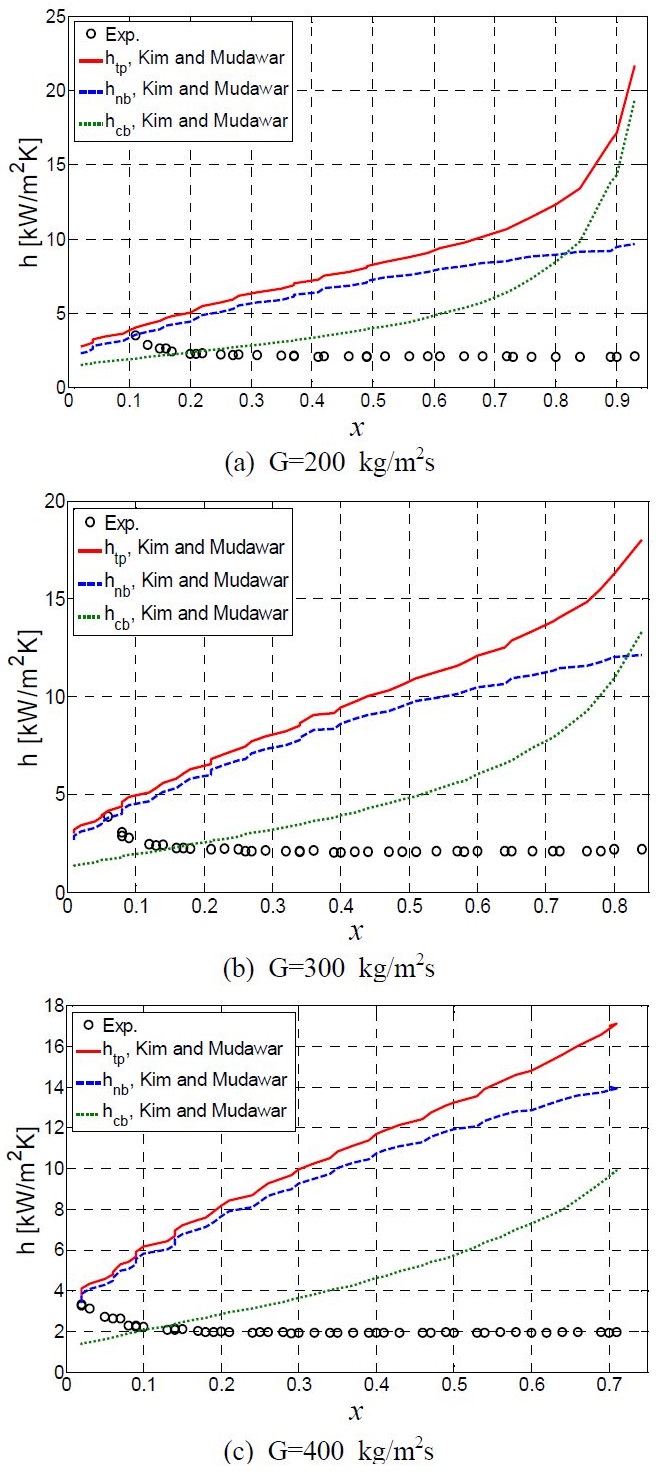
Figure 8은 각 질량 유속에서 식 (6)을 사용하여 예측한 열전달 계수와 실험에서 얻어진 열전달 계수를 비교하였다. Kim and Mudawar의 상관식에 의한 예측 결과를 보면 핵비등과 강제 대류 비등에 의한 열전달이 증기 건도의 증가에 따라서 증가하는 것으로 나타났다. 그리고 Kim and Mudawar의 상관식의 핵비등 열전달 계수는 다른 연구자들[11][17]의 상관식을 통해 계산된 핵비등 요소에 비해 그 값을 높게 예측하였다. 이러한 경향은 본 연구의 실험결과를 만족스럽게 예측하지 못하였다. 실험에서 얻어진 기존의 상관식이 본 연구의 결과를 잘 예측하지 못하는 것은 실험조건, 채널의 형상 그리고 작동 유체의 선정 등에서 차이가 발생되는 것으로 사료된다[12].
본 연구의 실험결과를 정확하게 예측하기 위해서는 핵비등에 의한 열전달 계수는 증기 건도가 증가함에 따라서 감소하여야 하며, 강제 대류 비등에 의한 열전달 계수는 건도 증가와 함께 증가하여야 될 것으로 판단된다. 향후 마이크로 채널 히트싱크의 효과적인 적용을 위해서는 열전달 특성을 충분하게 내포할 수 있는 상관식의 지속적인 개발이 요구된다.
4. 결 론
본 연구에서는 FC-72를 작동 유체로 사용하여 마이크로 채널에서의 비등 열전달에 관한 실험을 수행하였으며, 다음과 같은 결론을 얻었다.
- 1. 실험으로부터 얻어진 열전달 계수는 낮은 증기 건도(x < 0.2)에서는 급격히 감소하였으며, 이러한 경향은 핵비등에 의한 열전달이 지배적으로 작용하고 있음을 나타낸다. 그리고 증기 건도가 더욱 증가함에 따라 열전달 계수는 거의 일정하게 유지되었는데, 이것은 핵비등과 강제 대류 비등에 의한 열전달이 복합적으로 작용하고 있음을 의미한다.
- 2. 열전달 계수는 무차원 수인 비등수 그리고 대류수와 밀접한 관련이 있다. 핵비등이 지배적으로 작용하는 영역에서는 비등수의 영향이 크게 나타나며, 강제 대류 비등이 지배적으로 작용하는 영역에서는 대류수의 영향이 크게 나타나는 것으로 보인다.
- 3. 실험에서 얻어진 열전달 계수는 Kim and Mudawar[19]의 상관식에 의한 열전달 계수와 비교하였으나, 본 연구의 결과를 잘 예측하지 못하였다. 따라서 마이크로 채널에서의 열전달 특성을 정확하게 예측할 수 있는 상관식의 개발이 요구된다.
References
-
D. B. Tuckerman, and R. F. W. Pease, “High-performance heat sinking for VLSI”, IEEE Electron Device Letters, 2(5), p126-129, (1981).
[https://doi.org/10.1109/EDL.1981.25367]

- G. E. Moore, “Cramming more components onto integrated circuits”, Electronics, 38(8), p114-117, (1965).
- H. Moustaph, M. F. Zelesky, N. C. Baines, and D. Japikse, Concepts NREC, (2003).
- M. F. Wadel, Comparison of High Aspect Ratio Cooling Channel Designs for Rocket Combustion Chamber with Development of an Optimized Design, Technical Report No. TM-1998-206313, National Aeronautics and Space administration, Lewis Research Center, (1998).
-
M. Visaria, I. Mudawar, and T. Pourpoint, “Enhanced heat exchanger design for hydrogen storage using high-pressure metal hydride: part 1. Design methodology and computational results”, International Journal of Heat and Mass Transfer, 54(1-3), p413-423, (2011).
[https://doi.org/10.1016/j.ijheatmasstransfer.2010.09.029]

-
M. Visaria, I. Mudawar, and T. Pourpoint, “Enhanced heat exchanger design for hydrogen storage using high-pressure metal hydride: part 2. Experimental results, International Journal of Heat and Mass Transfer, 54(1-3), p424-432, (2011).
[https://doi.org/10.1016/j.ijheatmasstransfer.2010.09.028]

- J. G. Collier, and J. R. Thome, Convective Boiling and Condensation, 3rd Ed., Oxford University Press, (1994).
-
G. M. Lazarek, and S. H. Black, “Evaporative heat transfer, pressure drop and critical heat flux in a small vertical tube with R-11”, International Journal of Heat and Mass Transfer, 25(7), p945-960, (1982).
[https://doi.org/10.1016/0017-9310(82)90070-9]

-
Z. Y. Bao, D. F. Fletcher, and B. S. Haynes, “Flow boiling heat transfer of freon R11 and HCFC123 in narrow passages”, International Journal of Heat and Mass Transfer, 43(18), p3347-3358, (2000).
[https://doi.org/10.1016/S0017-9310(99)00379-8]

-
H. J. Lee, and S. Y. Lee, “Heat transfer correlation for boiling flows in small rectangular horizontal channels with low aspect ratios”, International Journal of Multiphase Flow, 27(12), p2043-2062, (2001).
[https://doi.org/10.1016/S0301-9322(01)00054-4]

- S. G. Kandlikar, “A model for correlation flow boiling heat transfer in augmented tubes and compact evaporators”, Journal of Heat Transfer, 112(1), p219-228, (1990).
-
J. S. Lee, and I. Mudawar, “Two-phase flow in high-heat-flux micro-channel heat sink for refrigeration cooling applications: Part II- heat transfer characteristics”, International Journal of Heat and Mass Transfer, 48(5), p941-955, (2005).
[https://doi.org/10.1016/j.ijheatmasstransfer.2004.09.019]

-
A. Megahed, “Local flow boiling heat transfer characteristics in silicon micro channel heat sinks using liquid crystal thermography”, International Journal of Multiphase Flow, 39, p55-65, (2012).
[https://doi.org/10.1016/j.ijmultiphaseflow.2011.09.003]

-
Y. S. Choi, T. W. Lim, and S. S. You, “Prediction methods for two-phase flow frictional pressure drop of FC-72 in parallel micro-channels”, Journal of the Korean Society of Marine Engineering, 38(7), p821-827, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.7.821]

-
Y. S. Choi, T. W. Lim, S. S. You, H. S. Kim, and H. S. Choi, “Boiling heat transfer characteristics of FC-72 in parallel micro-channels”, Journal of the Korean Society of Marine Engineering, 38(9), p1032-1038, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.9.1032]

- J. P. Holman, Experimental Methods for Engineering, 5th ed., Singapore, McGraw-Hill, (1989).
- M. M. Shah, “Chart correlation for saturated boiling heat transfer: Equations and further study”, American Society of Heating, Refrigerating, and Air Conditioning Engineers Transactions, 88, p66-86, (1982).
-
G. R. Warrier, V. K. Dhir, and L. A. Momoda, “Heat transfer and pressure drop in narrow rectangular channels”, Experimental Thermal and Fluid Science, 26(1), p53-64, (2002).
[https://doi.org/10.1016/S0894-1777(02)00107-3]

-
S. M. Kim, and I. Mudawar, “Universal approach to predicting saturated flow boiling heat transfer in mini/micro-channels – Part II. two-phase heat transfer coefficient”, International Journal of Heat and Mass Transfer, 64, p1239-1256, (2013).
[https://doi.org/10.1016/j.ijheatmasstransfer.2013.04.014]

-
S. W. Churchill, and R. Usagi, “A general expression for the correlation of rates of transfer and other phenomena”, American Institute of Chemical Engineers Journal, 18(6), p1121-1128, (1972).
[https://doi.org/10.1002/aic.690180606]