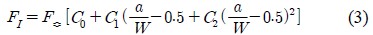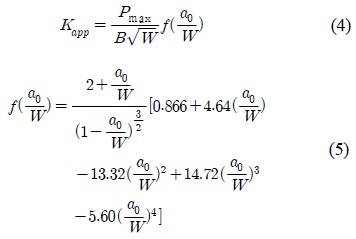Evaluation of tensile strengths and fracture toughness of plain weave composites

1.서 론

최근 복합재료는 해양수송기, 풍력발전 분야 및 차량의 경량화를 위해 주요 부품들의 중량 감소에 따른 연비향상, 제동 및 조향에 따른 에너지 절약 및 이산화탄소 배출을 최소화 하는 장점 때문에 그 수요가 증가하고 있다[1][2]. 다양한 복합재료 중 직물구조 복합재료는 복잡한 강화구조를 가지기 때문에 그 역학적 손상거동은 파악하기가 쉽지 않다. 따라서 지금까지 많은 연구자에 의해 여러 가지 접근법이 제안되었다[3]-[5]. 대표적인 예로, 홍창선 등[3]은 일방향 적층 복합재료를 대상으로 다양한 모드조건(모드 I, II, III)에서의 층간파괴 시험법을 제안하였고 Hochard 등 [4]-[5]은 직물구조 적층 복합재료를 대상으로 수학적 모델을 제안하고 모드 I 조건 하에서 파괴 특성을 예측하였다. 하지만 이상의 연구들은 국한된 종류의 복합재료에 해당되는 실험법으로, 적층 형태 및 종류가 달라지면 그 특성을 평가하거나 예측할 수 없다. 또한 복합재료 섬유간에 충진된 Matrix 특성을 정확히 고려하지 않아 실험결과와도 큰 차이를 보이고 있어 명확한 파괴거동 해석 수법이 확립되지 못한 실정이다. 하지만 아직까지 명확한 파괴거동 해석수법이 확립되어 있지 않다. 특히 조선구조재료의 기계적 특성과 더불어 직물구조 CFRP(Carbon Fiber Reinforced Plastic) 복합재료의 균열에 대한 저항 특성을 파악해두는 것은 조선 구조물의 건전성 평가를 위하여 대단히 필요하다. 일방향 연속섬유강화복합재의 경우에는 Hochard 등[6]이 개구형 변형양식에서 균열이 진전할 때 균열진전 저항특성을 파악하였으며, Xiao 등 [7]은 직물구조 GFRP(Glass Fiber Reinforced Plastic) 복합재료에 대하여 유한요소모델을 제안하여 손상진전 해석을 실시하여 보고하였으나 GFRP 단층판의 경우에 한하였다. Kzauro 등[8][9]은 섬유방향을 변화시킨 직물 CFRP 적층판의 파괴인성치와 AE(Acoustic Emission) 결과 값들과의 관계를 제시하였으나 파손 기구와의 연결성을 충분히 설명하지 못하였다. 이러한 배경에서 직물구조 CFRP 복합재료의 파괴 저항특성의 실험적 연구를 통해 명확한 파괴저항성의 평가가 이루어 져야 할 것이다.

한편, CFRP 복합재료가 구조물의 외층으로 사용될 경우, 폭에 비해 두께가 얇은 재료를 사용하므로 평면응력 파괴인성치(K_c)를 사용하였다.

Figure 1:

Fabric texture orientation of plain woven CFRP laminate composite

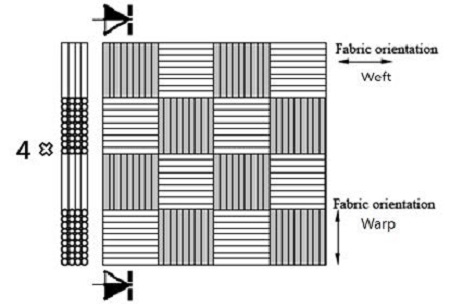
기존의 K_c는 주로 CT시험편(Compact tension specimen)을 이용하여 결정한다[10][11]. 본 연구에서는 평직구조의 CFRP 복합재료에 대하여 두께 3.5mm CT(Compact Tension) 시험편으로 평면응력 파괴인성 실험을 수행하였다. 이와 더불어 직물의 방향성에 따른 재료물성치의 변화를 살펴보고자 인장시험편(0°, 15°, 30°, 45°)을 제작하고 인장시험을 통해 필요한 재료물성치를 획득하였다. 나아가 이방성체 평직 CFRP 복합재료의 응력강도 보정계수를 적용하여 이를 금속재의 경우와 비교하였다. Figure 1에 본 연구에 사용된 평직 적층판의 구조를 나타내었다.

2.재료 및 실험방법

2.1 실험재료

국내 한국카본(주)에서 시판되는 직물구조(plain) 탄소섬유 프리프레그(woven carbon prepreg)인 WSN3K(두께 0.27mm)를 이용하여 실험재료로 사용하였으며 최종두께는 3.50 mm 이다. 적층판은 16층으로 오토클레이브(autoclave)에서 140℃, 60 kg/cm²의 온도와 압력에서 60분간 성형, 제작되었다. 프리프레그의 화학적 성분을 Table 1에 나타내었다.

Table 1:

Chemical compositions of prepreg (Wt. %)

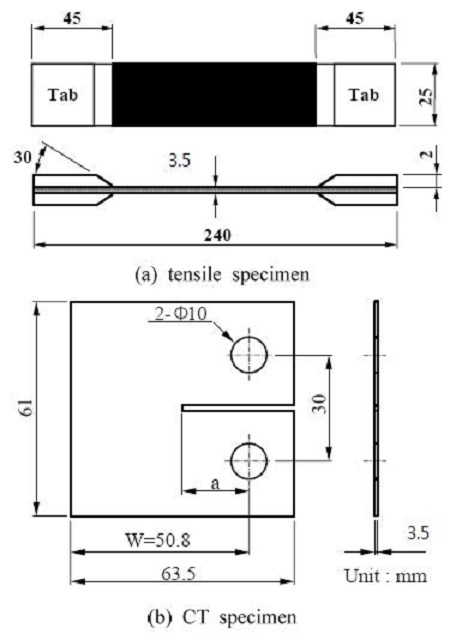
인장시험편은 ASTM D-3090-02를 참조하여 NC 머신으로 인장시험편을 제작 하였으며, 시험편 끝단은 인장 실험시 시험기의 그립으로부터 손상을 방지하기 위해 에폭시 수지인 아랄다이트(araldite)로 GFRP 탭(두께: 2mm)을 부착하였다. 시험편의 탭 부위에 접합강도의 강화와 슬립 방지를 위해 #100의 에머리-페이퍼로 거칠게 연마하여 GFRP 탭을 부착 후 K사의 HY-8000S 전기로에서 100℃로 30분간 후처리를 수행하였다.

파괴인성시험에 사용된 CT 시험편은 ASTM E-647-02 추정법에 따라 NC머신을 이용해 폭 1mm 노치를 삽입하였다. 이때 매우 날카로운 균열을 삽입하여야 하지만 기계가공에 한계가 있으므로 3점 밴딩(three point bending) 피로시험으로 피로균열을 a₀/W=0.4가 되게 하였다. 시험편의 형상은 Figure 2에 나타내었다.

Figure 2:

Specimen configurations

2.2 실험방법

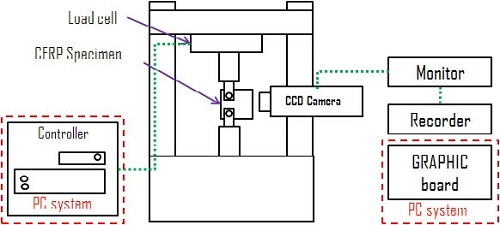
재료의 인장강도, 연신률 등의 기본재료 물성치를 측정하기 위하여 인장시험을 수행하였다. 사용된 시험기는 Shimadzu사의 25 ton 인장시험기로서 Figure 3에 시험기의 형상을 나타내었다.

파괴인성 시험편의 경우 두께가 얇기 때문에 좌굴이 발생할 수 있으므로 편심방지용 가이드 지그를 사용하여 고정하였다. 상온에서 0.2 mm/min 변위제어로 시험을 수행하였다. 인장 및 파괴인성 시험동안 균열발생 및 진전거동과 기지 및 섬유의 표면손상과정을 소형 CCD 카메라를 사용하여 모니터링 하였다. Figure 4에 실험장치의 개략도를 나타내었다.

Figure 3:

Appearance of tensile tester

Figure 4:

Schematic diagram of experimental apparatus for fracture toughness test

3.평직 CFRP 복합재료의 응력확대계수의 계산

3.1 이방성체 응력확대계수 평가

균질탄성체에 있어서 CT 시험편의 경우, 응력확대계수 K는 다음 식과 같이 나타낼 수 있다.

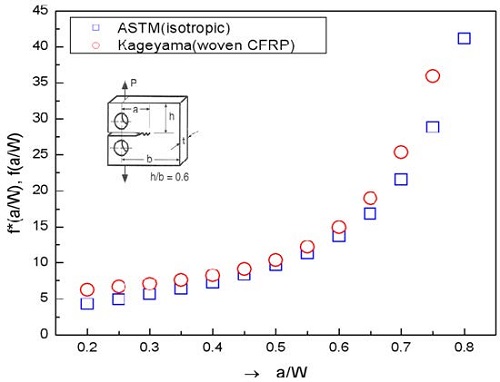
여기서, W는 시험편의 폭이며 a는 균열길이이다. 그리고 f(a₀/W)는 유한 폭에 대한 형상보정계수이다. 섬유강화복합재료에서 강화섬유 배열방향에 따라 현저한 이방성이 존재하고 있으므로 식 (1)과 같은 균질탄성체에 대한 K의 적용은 곤란하다. 따라서 복합재료의 이방성을 고려한 새로운 형상보정계수 f*(a₀/W)를 산출해야 한다.

3.2 이방성체 응력확대계수의 계산

섬유강화 복합재료에서 강화섬유의 배열로 인해 현저한 이방성이 존재하고 있으므로 ASTM에 제시된 균질탄성체에 대한 K의 적용은 곤란하다. 이에 평직 CFRP 복합재료에 대한 응력확대계수는 Kageyama [8]등에 의한 실험식에서 다음 식 (2)로 나타낼 수 있다.

이때, 형상보정계수 F_I 는 식 (3)과 같이 계산된다.

여기서, P는 하중, B는 두께, W는 폭, 그리고 a는 균열길이이며 F_≎는 동일 a/W에 해당하는 균질탄성체의 형상보정계수 값이다.

C₀, C₁ 그리고 C₂는 섬유방향을 나타내는 보정계수로 섬유배열방향에 따라 달라진다. Table 2에 섬유배열방향별 보정계수를 정리하여 나타내었다[8].

Figure 5는 ASTM에서 제시하는 균질탄성체의 f(a₀/W)의 선도와 함께 비교하여 나타낸 선도로서 섬유강화 복합재료의 형상보정계수와는 차이를 보이는 것을 확인 할 수 있었다.

Table 2:

Coefficient Ci of compact specimen

Figure 5:

Variations of f(a0/W) in Plain woven CFRP composite

4.실험결과 및 검토

4.1 인장시험

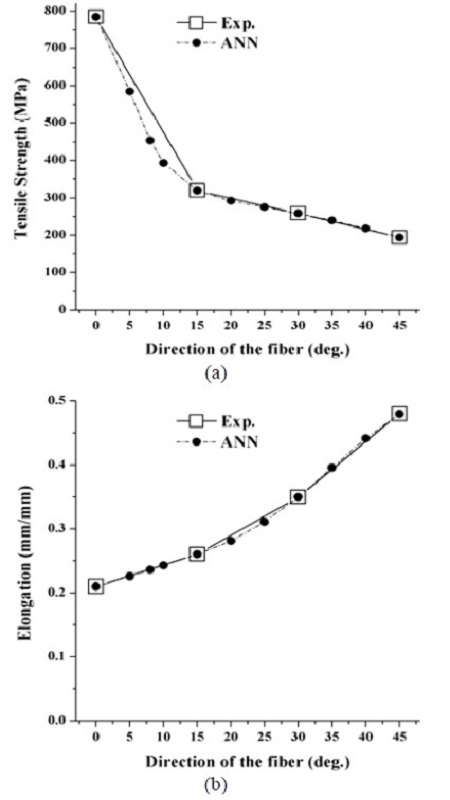
위사(weft) 섬유방향을 기준으로 하중방향에 대한 섬유 배열 방향별(0°, 15°, 30°, 45°) 3회의 시험을 수행한 후 평균한 인장시험 결과를 Table 3에 나타내었으며, Figure 6에 섬유방향과 인장강도 및 연신율의 관계를 나타내었다. 시험결과, 45° 방향의 인장강도가 가장 취약하였으며 0° 방향의 인장강도에 비해 약 28% 감소하는 것을 확인할 수 있었다. 이와는 반대로 연신율의 경우, 0° 방향의 연신율이 가장 낮았으며 45° 방향의 연신율이 가장 높게 나타났다.

이는 0° 방향으로 인장하중이 가해질 경우 위사는 다소 변형률이 적은 접착분리(debonding) 현상이 나타나며, 경사(warp)은 섬유파손(fiber breakage)를 일으켜 파괴되지만, 45° 방향의 경우는 위사가 접착분리와 섬유파손 현상이 함께 나타나므로 그만큼 변형률이 커지게 된다. Figure 7에 파괴된 인장시험편의 파면을 각각 나타내었다.

Figure 6:

Relationship between direction of fiber and tensile strength

Figure 7:

Fracture surface of 0° fabric orientation under the tension loading

섬유의 배열 방향에 따른 재료물성치의 변화는 비선형적으로 변화하게 된다. 또한 시험편 제작의 제한 등으로 다양한 직조 방향에 관한 재료 물성을 얻기 어려움이 있고, 섬유와 고분자의 비선형 관계에서 최종 물성이 결정되는 복합소재에서는 물성을 예측하는데 어려움이 있다. 복합소재의 비선형 특성을 인공신경망(Artificial Neural Network; ANN)을 활용하여 시험이외의 값들을 예측하였다. 본 연구에서 적용한 신경망 이론은 다층 퍼셉트론(multilayer perceptron) 개념이 도입된 역전파 알고리즘을 사용하였다[1][2]. 신경망 학습의 입력 인자는 섬유방향을 선택하였고, 출력 인자는 인장강도와 연신율이 된다. 신경망 학습을 통하여 얻어진 예측 값이 실제 실험값을 잘 나타내며, 특히 실험이 이루어지지 않은 부분의 비선형성을 나타내는 것을 확인 할 수 있다(Figure 6).

Table 3:

Comparison of material properties on fiber orientation

4.2 파괴인성시험

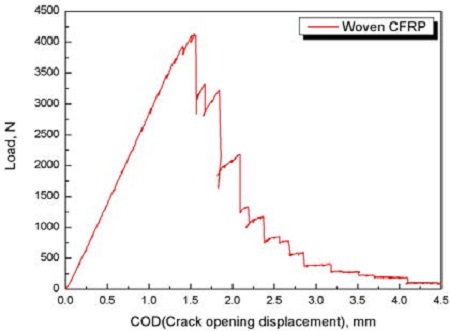
균열개구변위(Crack Opening Displacement, COD)값을 사용하여 평직 CFRP 복합재료(0° orientation)에 대한 하중-COD 선도를 Figure 8에 나타내었다. 또한 하중-COD 선도를 이용한 평면응력 파괴인성치를 결정하기 위해 최대하중 (P_max)과 초기균열길이(a₀)에 의한 ASTM E1820의 평면응력 파괴인성치 결정법을 사용하여 K_app를 구하였다. 초기조건은 균열길이 (a₀=20.32 mm), 시편 폭 (W=50.8 mm), 시편 두께 (B=3.5 mm) 이다.

Figure 8:

Load-COD curves for plain woven CFRP composite of CT specimens

K_app를 구하기 위하여 사용한 식은 다음과 같다.

여기서, f(a₀/W)는 시험편의 형상계수로서 위의 식에 사용될 형상계수 f(a₀/W)는 ASTM에서 제시하는 균질탄성체에 대한 형상계수이다.

따라서 등방성으로 가정하여 계산된 균질탄성체의 형상계수 f(a₀/W)를 현저한 이방성을 가지는 평직 CFRP 복합재료의 파괴인성치를 구하는데 직접 적용시키는 것은 무리가 있다. 따라서 3장에 서술된 Kageyama 등이 제시한 이방성 평직 CFRP 복합재료의 형상보정계수 f*(a₀/W)를 적용하였다. K_app를 구하기 위해 5% 옵셋(offset) 하중 값(PQ)을 사용하였고 균열길이와 시편의 폭, 두께는 초기조건의 값을 사용하였다. 총 3회의 시험을 수행하여 Table 4에 정리하여 나타내었다. 시험결과, K_app는 약 37.62MPa√m 로서 ASTM에서 제시하는 형상보정계수를 적용한 값과 약 15% 정도 차이가 나는 것을 확인할 수 있었다.

Table 4:

Results of fracture toughness

5. 결 론

평직 CFRP 복합재료에 대하여 하중방향에 대한 직물의 방향성의 변화가 파손강도에 미치는 영향을 알아보기 위하여 4가지의 직물방향에 따른 인장시험을 수행하였다. 또한 평직 CFRP 복합재료의 횡방향 균열에 대한 파괴인성치를 평가하기 위하여 파괴인성시험을 수행하였으며, 이방성을 고려한 형상보정계수를 적용하여 파괴인성치를 비교하였다. 본 연구를 통하여 다음과 같은 결과를 얻었다.

(1) 인장시험을 통해 살펴본 하중방향에 따른 직물의 방향성의 변화가 재료물성의 변화에 영향을 미친다는 것을 확인하였다. 45° 방향의 인장강도는 0°방향의 인장강도에 비해 약 28% 감소하였으나, 연신율은 약 43% 증가하는 경향을 나타내었다. 이는 직물을 구성하는 위사와 경사의 파손양상이 하중방향에 대해 직물의 방향이 변함에 따라 파손 양상도 변하기 때문으로 판단된다. 따라서 향후 직물의 방향성을 고려한 파괴저항성 평가에 대한 연구도 필요할 것으로 판단된다.

(2) Kageyama등이 제시한 형상보정계수를 적용한 결과, 평직 CFRP 복합재료의 K_app는 약 37.62MPa√m 로 평가되었다. 이는 ASTM에 제시된 균질탄성체 형상보정계수를 적용한 결과 값과 약 15% 차이를 보이는 바, 이방성체 CFRP 복합재료의 파괴인성 평가시 균질탄성체 형상보정계수를 적용한다면 그 결과 값이 다소 과소평가될 수 있다고 판단된다.

(3) 이방성체 형상보정계수 f*(a₀/W는 ASTM에 제시된 균질탄성체의 형상보정계수와는 상당한 차이가 나타남을 확인하였다. 따라서 향후 복합재료의 파괴저항성 또는 균열성장시험을 위해서는 시험편의 기하학적 형상, 이방성, 직교이방성 등의 조건을 고려한 유한요소 해석을 병행하여 보다 정확한 형상보정계수를 도출하는 것이 필수적이다.

References

• O. H. Kwon, S Xu., and M. Sutton, “Evaluation of the damage mechanism in CFRP composite using computer vision”, The Korean Socienty of Marine Engineering, 34(5), p686-694, (2010). [https://doi.org/10.5916/jkosme.2010.34.5.686]
• S. Y. Bae, B. S. Kim, W. J. Kim, and M. Y. Kim, “Structural design of 3MW wind turbine blade, and their structural safety evaluation”, The Korean Socienty of Marine Engineering Conference, p289-290, (2010), (in Korean).
• C. S. Hong, “Test method for intralaminar fracture of composite”, The Korean Society of Mechanical Engineers, 30(2), p172-179, (1990), (in Korean).
• C. Hochard, P. A. Aubourg, and J. P. Charles, “Modelling of the mechanical behaviour of woven fabric CFRP laminates up to failure”, Composites Science and Technology, 61, p221-230, (2001). [https://doi.org/10.1016/S0266-3538(00)00199-8]
• S. T. Peters (Ed), Handbook of Composites, 2nd ed, Chapman and Hall, p794-809, (1998).
• C. Hochard, “Optimum design of laminated composite structures”, Composite Structures, 63(2), p159-165, (2004). [https://doi.org/10.1016/S0263-8223(03)00144-2]
• J. Xiao, and C. Bathias, “Modified tan’s model for the strength prediction of woven laminates with circular holes”, Composites Engineering, 3(10), p961-963, (1993). [https://doi.org/10.1016/0961-9526(93)90004-4]
• K. Kzauro, N. Katsunobu, S. Shoji, and F. Shunji, “Fracture toughness and acoustic emission of Carbon-Cloth/Epoxy composite”, The Japan Society of Mechanical Engineers, 50, p1260-1266, (1984).
• D. H. Pahr, and F. G. Rammerstorfer, “Experimental and numerical investigations of perforated CFRP woven fabric laminates”, Composites Science and Technology, 64, p1403-1410, (2004). [https://doi.org/10.1016/j.compscitech.2003.11.001]
• J. Wang, P. J. Callus, and M. K. Bannister, “Experimental and numerical investigation of the tension and compression strength of un-notchedand notched quasi-isotropic laminates”, Composite Structures, 64(3-4), p297-306, (2004). [https://doi.org/10.1016/j.compstruct.2003.08.012]
• G. B. Murri, and J. R. Schaft, “Fatigue life methodology for tapered hybrid composite flexbeams”, Composites Science and Technology, 66(3-4), p499-508, (2006). [https://doi.org/10.1016/j.compscitech.2005.06.010]
• K. Gurney, "An introduction to neural networks", University College London Press, p45-48, (1997).