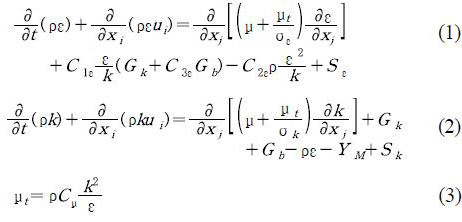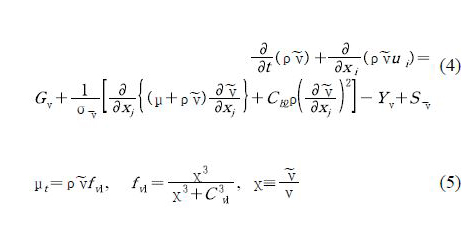Numerical analysis of turbulent flows in the helically coiled pipes of heat transfer
The flow analysis has been made by applying the turbulent models in the helically coiled tubes of heat transfer. The k-ε and Spalart-Allmaras turbulent models are used in which the structured grid is applied for the simulation. The velocity vector, the pressure contour, the change of residuals along the iteration number and the friction factors are simulated by solving the Navier-Stokes equations to make clear the Reynolds number effect. The helical tube increases the centrifugal forces by which the wall shear stress become larger on the outer side of the tube. The centrifugal force makes the heat transfer rate locally larger due to the increase of the flow energy, which finds out the close relationship between the pressure drop and friction factor in the internal flow. The present numerical results are compared with others, for example, in the value of friction factor for validation.
초록
열교환기의 나선형 튜브에 난류모형을 적용하여 유동해석을 수행하였다. 난류모형은 Spalart-Allmaras과 k-ε이고 시뮬레이션에는 정렬격자를 적용하였다. 레이놀즈 수 영향을 규명하기 위하여 Navier-Stokes 방정식을 풀어 속도벡터, 압력, 잔차, 마찰계수를 재연하였다. 나선형튜브는 원심력을 증가하여 튜브의 바깥부분에 벽전단 응력을 크게 하였다. 열전도율과 마찰저항의 증가는 곡률에 기인하며 튜브의 내부방향으로는 벽 전단응력이 감소했다. 원심력은 유체의 에너지를 증가시켜서 바깥쪽으로 열전도율을 증가시켰고 이는 내부유동의 압력강하 및 관마찰계수가 상호 밀접한 관계가 있음을 규명하여 주었다. 본 수치결과는 검증을 위하여 타 계산에서 얻어진 마찰계수 결과와 비교하였다.
Keywords:
Helically coiled pipes, Numerical analysis, Turbulent flow, Heat transfer, Finite volume method, 나선코일관, 수치해석, 난류유동, 열교환기, 유한체적법1. 서 론
나선형 곡관에서의 열전도는 튜브내의 마모도 및 원자로 증기발생기 전열관의 평가에 대단히 중요하다. 강제대류 튜브 열교환기는 원자로 설비에서 광범위하게 찾아 볼 수 있으며, 이러한 나선 계통의 열전달과 압력강하에 관한 연구는 Seban[1], White[2], Mishra[3], Ali[4], Ito[5] 등에 의해서 이루어졌다. 열전도 증가를 위하여 튜브의 형상설계를 나선형으로 하고 내부유동에서의 원심력을 이용하여 나선중심의 외부방향으로 압력구배를 형성한다. 원형나선의 내부압력 비대칭성 구배는 결국은 2차 유동을 형성하고 바깥부분의 속도를 증가시키는데 이는 열전달을 크게 하여 성능을 향상시키게 된다. 나선형 튜브에서 2차 유동은 관 바깥부분의 유체속도를 증가시키고 관 안쪽부분의 주유동 속도를 감소시킨다. 이는 내부유동의 압력강하나 관 마찰계수와 밀접한 관계를 가지고 있다. 전산유동해석을 열전도 문제에 적용한 기법으로는 LES[6] (Large Eddy Simulation) 및 직접수치모사[7][8](Direct Numerical Simulation)가 있으며 수치해석을 통해 관내의 2차 유동특성과 난류에 대한 연구가 이루어지고 있다. 단상유동에서 실험적 방법으로 코일의 반경비 변화에 따른 열전달 상관도를 제시한 연구가 이루어졌고[9] Reynolds수가 커질 경우 이론적인 결과와 실험적인 결과 사이에는 차이가 있으며 그 계산과정은 복잡하다. 2차 유동에서 곡률비가 커지면 섭동해석(perturbation analysis )으로 마찰손실이 매개변수에 대한 함수임을 알 수 있다. 한편 마찰손실이 곡률매개변수에 의존하고 있고 이들 섭동해석은 낮은 레이놀즈 수에서 성립한다. 2차 유동장은 주로 경계층으로 영역을 구분하여 점성과 비점성으로 구분하여 해석하고, 근사경계층 해들을 얻을 수 있다. 본 계산에서는 나선형 관내의 열전도 유동특성에 대하여 레이놀즈 수와 코일의 반경비가 튜브의 국부적인 난류특성에 미치는 영향을 상용코드인 FLUENT를 이용하여 조사하였다. 본 연구의 목적은 계산결과를 이용하여 열교환기와 같은 산업설비의 안전과 성능을 평가하는 기초자료로 활용하는데 있다.
2. 수치시뮬레이션
2.1 기본방정식과 수치조건
기본방정식은 Navier-Stokes 방정식이며 유한체적법의 수치기법으로 격자를 만들어 계산을 수행하였다.
k-ε 을 사용한 수송방정식[10]은
Configuration and grid of helically coiled pipes
Spalart-Allmaras[1]을 사용한 수송방정식은
2.2 격자생성과 경계조건
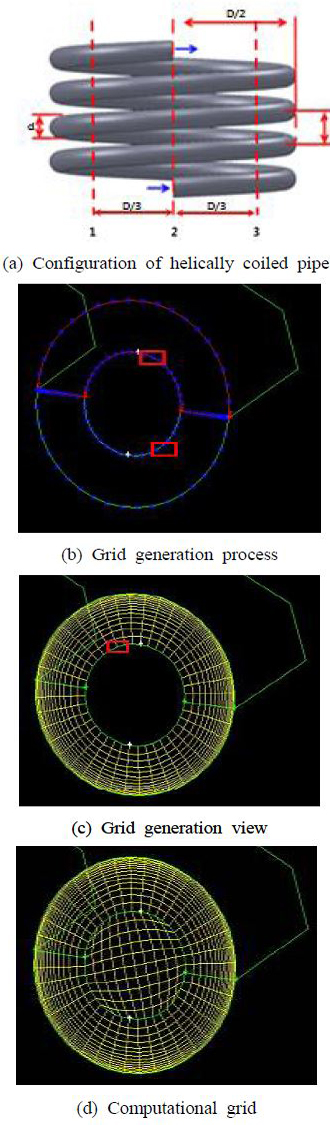
Figure 1은 수치해석을 위한 격자를 보여주고 있다. 갬빗 모듈을 사용해서 정렬격자를 구성하였다. 격자생성은 블린연산(boolean operation)으로 만들었고 혼합체적을 이용하여 굴곡을 주었다. 모든 원천에는 쿠퍼격자법(cooper meshing scheme)을 이용하여 평행을 유지했고 그 밖의 면에는 부도해법 (submap meshing scheme)을 사용하였다. 요소는 Hex/wedge, 형태는 Cooper를 주었다. 혼합을 해서 만든 면은 쓸기 기능을 이용하여 경사면을 생성하였다. 내부의 격자는 그래픽 창에서 최종이미지 랜더링 모형(render model)을 사용하였다. 격자수는 576,704개의 셀로 구성하였다. 격자생성에서는 피치와 회전을 이용하여 선과 원의 중심점을 관통하게 만들었고 첫 번째는 라인스케치를 두 번째는 원스케치 개념을 이용하였다.
경계조건은 입구면, 출구면, 벽면에 속도, 압력 및 구배조건을 부여하였고 공간내부에는 연속형체 조건을 주었다. 균일한 입구속도 및 균일한 열유속을 적용했고, 벽면에는 점착조건, 벽근처에는 저레이놀즈 수 모형을 적용하였다.
3. 수치해석결과 및 토의
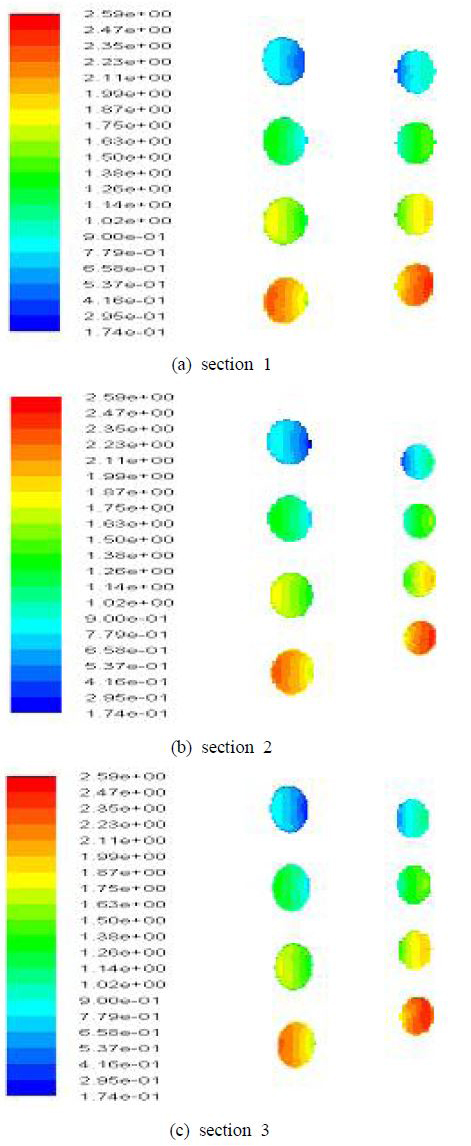
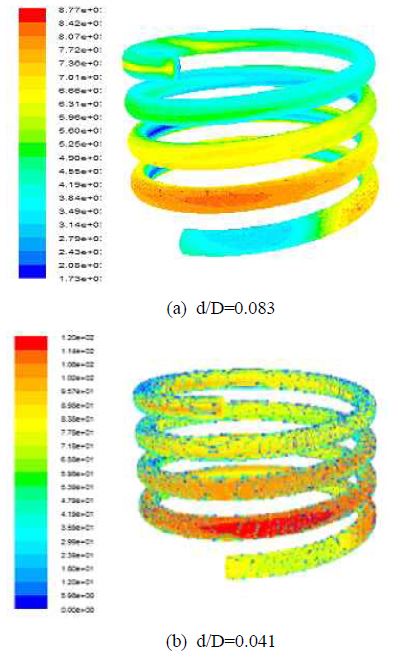
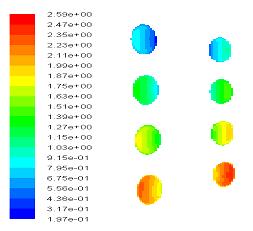
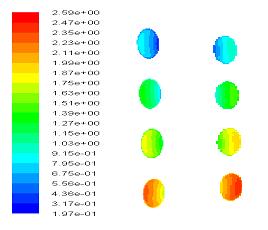
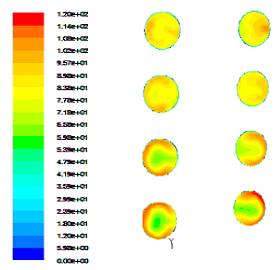
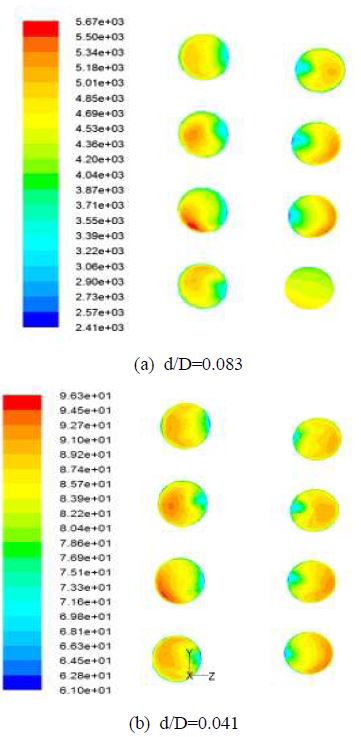
본 연구에서는 레이놀즈 수와 나선곡률비를 경우별로 나눠서 2차유동과 그 특성에 영향을 주는 인자를 적용하였다. 레이놀즈 수는 10,000, 25,000, 50,000, 100,000이고, 곡률비는 0.083, 0.041, 0.0207 이다. 난류 모델은 Spalart-Allmaras 모형과 곡률과 유동회전에서 적용이 가능한 k-ε 모형을 적용하였다. Figure 2는 레이놀즈 수 10,000에서 난류모형 Spalart-Allmaras 를 적용했을 때의 압력분포를 보여주고 있다. 여기서 section의 표시는 Figure 1(a)에 표시되어 있다. Figure 3은 레이놀즈 수 10,000에서 속도분포를 보이고 있는데 균속의 입구유동에 의해 유동 진행 방향으로 근거리에서는 관속의 원심력이 약하게 나타나며 벽쪽으로 경계층이 점차 증가함을 보이고 있다. 그리고 유동이 진전함에 따라 원심력이 점차 성숙하게 되고 이에 따라 튜브 안쪽에서 바깥쪽으로 서로 반대방향으로 회전하는 2차와류가 한쌍 생성되며 이것은 축방향 속도분포에 영향을 미치게 된다. s/d가 중간부근에서는 이미 원심력이 충분히 발달하여 축방향 모멘텀과 균형을 이루어 유동분포가 거의 변하지 않고 완전히 발달하여 수렴하는 것으로 판단된다. 여기서 s는 튜부축 방향좌표, d는 직경을 의미한다. Figure 4는 레이놀즈 수 25,000에서 난류모형 Spalart- Allmaras 를 적용했을 때의 압력분포를 보여주고 있다. 축방향 유동분포에서 튜브 입구에서 s/d가 증가함에 따라 원심력의 영향이 증가하여 이로 인해 바깥쪽의 유속이 빨라져서 튜브바깥쪽에서 열전도 효율이 크게 증가하고 튜브 안쪽에서는 반대로 된다. Figure 5는 레이놀즈 수 50,000에서 난류모형 Spalart-Allmaras 를 적용했을 때의 압력분포를 보여주고 있다. 앞에서 보여준 레이놀즈수 10,000, 25,000과 비교하면 레이놀즈 수가 증가하게 되면서 축방향 모멘텀이 증가하게 되고 원심력의 상대적 효과가 작아지게 된다.
Pressure contours at Re=10,000 for Spalart-Allmaras turbulence model
Velocity contour at Re=10,000 with curvature ratios of d/D
Pressure contours at Re=25,000 for Spalart-Allmaras model
Pressure contours at Re=50,000 Spalart-Allmaras model
Velocity contours at Re=100,000 for Spalart-Allmaras model
Velocity contours for k-ε at Re=100,000
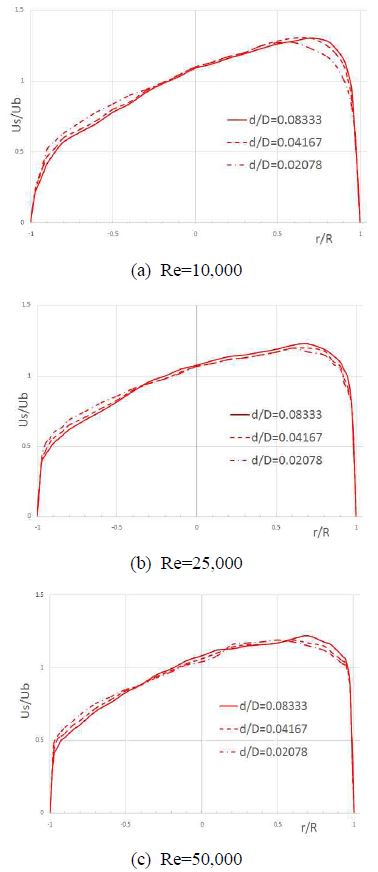
Figure 6, Figure 7은 레이놀즈 수 100,000에서 각각 Spalart-Allmaras, k-ε을 적용했을 때의 속도분포이다. 완전 발달한 난류유동의 경우로 볼 수 있다. Figure 7 에서는 곡률반경에 따른 결과의 차이를 볼 수 있다. Figure 8은 레이놀즈 수와 곡률반경에 따른 축방향의 속도이다. 완전 발달된 영역에서 튜브관속의 수평방향 속도분포를 나타낸다. 각 레이놀즈 수에서 곡률반경이 증가함에 따라 원심력의 영향이 커지고 이에 따라 관 바깥쪽의 속도가 커지며 관 안쪽의 속도가 감소함을 알 수 있다.
Axial Velocity (inner wall at r/R=-1, outer wall r/R=1)
수치결과의 검증을 위하여 레이놀즈 수 100,000 에서 마찰계수(friction factor)를 비교하였다. d/D= 0.083 에서 0.030(White[2]), 0.025(Ali[4]), 0.028 (Ito[5])이었는데 본 결과는 0.027을 보이고 있다. 그리고 d/D=0.041에서는 0.028 (White[2]), 0.025 (Ali[4]), 0.024 (Ito[5])이었는데, 본 결과는 0.026를 보이고 있다. 계산에서의 잔차 값은 10-7∾10-8로 수치적으로 수렴함을 보여 주었다.
4. 결 론
1) 나선형 관내의 열전도 유동특성에 대하여 레이놀즈 수와 코일의 반경비가 튜브의 국부적인 난류특성에 미치는 영향을 상용코드인 FLUENT를 이용하여 조사하였다.
2) 열전도율과 마찰저항의 증가는 곡률에 기인하며 튜브의 내부방향으로는 벽 전단응력이 감소했다. 원심력은 유체의 에너지를 증가시켜서 바깥쪽으로 열전도율을 증가시켰고 이는 내부유동의 압력강하나 관 마찰계수와 밀접한 관계가 있음을 알 수 있었다.
3) 3차원 유동해석을 통해 레이놀즈 수와 나선형 코일의 반경비가 튜브의 열전도에 국부적으로 영향을 미치고 있음을 알 수 있었다. 난류모형 k-ε과 Spalart-Allmaras을 적용하여 상호 비교하였다.
References
-
R. A. Seban, and E. F. McLaughlin, “Heat transfer in tube coils with laminar and turbulent flow”, International Journal Heat Mass Transfer 6, 6(5), p387-395, (1963).
[https://doi.org/10.1016/0017-9310(63)90100-5]
- C. M. White, “Fluid friction and its relation to heat transfer”, Transaction Institute Chemical Engineering(London), 10, p66-86, (1932).
-
P. Mishra, and S. N. Gupta, “Momentum transfer in curved pipes, 1. newtonian fluids”, Industrial Engineering Chemical Process Des. Dev, 1, p130-137, (1979).
[https://doi.org/10.1021/i260069a017]
-
S. Ali, “Pressure drop correlations for flow through regular helical coil tubes”, The Japan Society of Fluid Mechanics and Elsevier Science, 28(4), p295-310, (2001).
[https://doi.org/10.1016/S0169-5983(00)00034-4]
- H. Ito, “Friction factors for turbulent flow in curved pipes”, Transaction Am. Society Mechanical Engineering. Journal Basic Engineering D81, p123-134, (1959).
-
B. J. Boersma, and F. T. M. Nieuwstadt, “Large-eddy simulation of turbulent flow in a curved pipe”, Journal Fluids Energy, 118, p248-254, (1996).
[https://doi.org/10.1115/1.2817370]
-
C. Moulinec, M. J. B. M. Pourquié, B. J. Boersma, T. Buchal, and F. T. M. Nieuwstadt, “Direct numerical simulation on a cartesian mesh of the flow through a tube bundle”, International Journal of Computational Fluid Dynamics, 18(1), p1-14, (2004).
[https://doi.org/10.1080/1061856031000140211]
-
J. H. Bae, J. Y. Yoo, and H. Choi, “Direct numerical simulation of turbulent heat transfer to fluids at supercritical pressure flowing in vertical tubes”, Transactions of the Korean Society of Mechanical Engineers B, 28(11), p1302-1314, (2004), (in Korean).
[https://doi.org/10.3795/KSME-B.2004.28.11.1302]
-
R. C. Xin, A. Awwad, Z. F. Dong, and M. A. Ebadian, “An experimental study of single-phase and two-phase flow pressure drop in annular helicoidal pipes”, International Journal Heat Fluid Flow, 18, p482-488, (1997).
[https://doi.org/10.1016/S0142-727X(97)80006-9]
- B. E. Launder, and D. B. Spalding, Lecture in Math Models of Turbulence, Academic Press, London, England, (1972).
-
P. R. Spalart, and M. Shur, “On the sensitization of turbulence models to rotation and curvature”, Aerospace Science Technology, 1(5), p297-302, (1997).
[https://doi.org/10.1016/S1270-9638(97)90051-1]