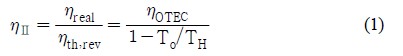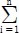[ Article ]

Journal of the Korean Society of Marine Engineering - Vol. 37, No. 8, pp.829-835

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Nov 2013

Received 14 Aug 2013 Revised 03 Sep 2013 Accepted 03 Sep 2013

DOI: https://doi.org/10.5916/jkosme.2013.37.8.829

Exergy analysis of R717 high-efficiency OTEC cycle

YoonJung-In¹ ; SonChang-Hyo^† ; YangDong-Il² ; KimHyeon-Uk³ ; KimHyeon-Ju⁴ ; LeeHo-Saeng⁵

1Department of Refrigeration and Air Conditioning Engineering, Pukyong National University 2Graduate School of Air Conditioning Engineering, Pukyong National University 3Graduate School of Air Conditioning Engineering, Pukyong National University 4Korea Advanced Institute of Science and Technology 5Korea Advanced Institute of Science and Technology

R717용 고효율 해양온도차 발전 사이클의 엑서지 분석

Correspondence to: ^† Department of Refrigeration and Air Conditioning Engineering, Pukyong National University, Yongdang-dong, Nam-gu, Busan, 608-739, Korea, E-mail: sonch@pknu.ac.kr, Tel: 051-629-6180

This paper describes an analysis on exergy efficiency of proposed high-efficiency R717 OTEC power system to optimize the design for the operating parameters of this system. The operating parameters considered in this study include outlet pressure in an evaporator and high turbine, inlet pressure condenser and vapor quality at cooler outlet, respectively. The main results are summarized as follows : As the outlet pressure in an evaporator and vapor quality at cooler outlet of R717 OTEC power system increases, the exergy efficiency of this system increases, respectively. But outlet pressure in the high turbine, inlet pressure in the condenser of R717 OTEC power system increases, the exergy efficiency of this system decreases, respectively. And, incase of exergy efficiency of this OTEC system, the effect of inlet pressure in an evaporator and outlet pressure in the high turbine on R717 OTEC power system is the largest and the lowest among operation parameters, respectively.

초록

본 논문은 제안된 고효율 R717용 해양온도차 발전 시스템의 운전변수에 대한 최적의 설계를 위해 엑서지 효율을 이론적으로 분석하였다. 본 연구에서 고려된 작동변수로는 증발기 출구압력, 고단터빈 출구압력, 응축기 입구압력 그리고 냉각기 출구건도이다. 분석한 결과를 요약하면 다음과 같다. R717용 OTEC 발전 사이클의 증발기 출구압력, 냉각기 출구건도가 증가할수록 엑서지 효율은 증가한다. 그러나 고단터빈 출구압력, 응축기 입구압력이 증가할수록 엑서지 효율이 감소한다. 그리고 이러한 작동변수들 중에서 증발기 출구압력이 R717용 OTEC 발전 사이클의 엑서지 효율에 가장 크게 영향을 미치고, 고단터빈 출구압력이 가장 적게 영향을 미친다.

Keywords:

R717, High-Efficiency, Ocean Thermal Energy Conversion Power Cycle, Exergy Analysis, 암모니아, 고효율, 해양온도차 발전 사이클, 엑서지 분석

1. 서 론

해양온도차(Ocean Thermal Energy Conversion, 이하 OTEC) 발전은 낮은 시스템 효율에도 불구하고, 청정에너지원으로서 심층수와 표층수를 해양으로부터 직접 얻을 수 있는 등의 장점으로 인해 이와 관련된 연구가 세계적으로 다양하게 진행되고 있는 실정이다. 해양의 표층수와 심층수의 온도차를 랭킨사이클에 적용하여 동력을 얻고, 이 동력을 발전기 구동에 이용하여 전기를 생산하는데, 이 기술을 적용한 시스템을 해양온도차 발전사이클 (OTEC power cycle)이라 한다.

Figure 1:

Schematic of high-efficiency R717 OTEC power cycle proposed in this study[1]

지금까지 많은 연구자[1]-[11]들은 고효율 OTEC 발전 시스템 개발을 위해 연구를 진행해 오고 있다. 우선, Kalina et al. [8]는 OTEC 발전 사이클의 큰 비중을 차지하는 열교환기(증발기와 응축기)의 효율을 향상시키기 위해서 암모니아-물의 혼합물을 작동유체로 사용하였다. 또한, Uehara et al. [9]는 Kalina [8]등과 마찬가지로 암모니아-물 혼합물의 작동유체를 사용하고, 다단터빈, 재생기, 재열기, 분리기 등의 기기를 OTEC 발전 사이클에 적용하였다.

본 연구에서는 제안한 고효율 OTEC 발전 사이클의 엑서지 특성을 분석 및 파악하기 위해 HYSYS [13] 프로그램을 이용하여 R717용 OTEC 발전시스템을 모사하고, 각각의 변수에 대한 영향을 분석하였다. 이를 통해 본 연구에서 제안하는 고효율 OTEC 발전 사이클에 대한 기초 설계 자료를 제공하고자 한다.

2. OTEC 사이클의 장치도 및 성능분석

2.1 OTEC 사이클의 장치도

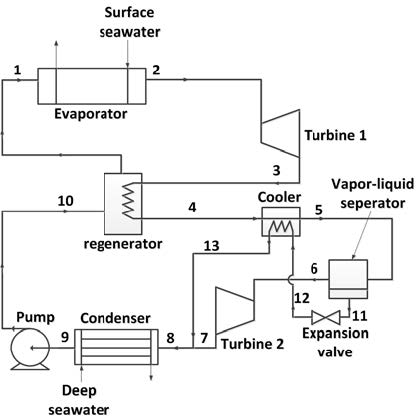
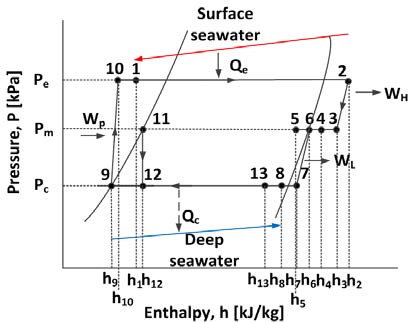
Figure 1은 본 연구에서 제안하는 고효율 OTEC 발전 사이클의 장치도를 나타낸 것이고, Figure 2는 상태점을 P-h 선도상에 나타낸 것이다. Figure 1에서처럼 냉각기, 재생기, 팽창밸브, 분리기 등을 채용한 고효율 OTEC 발전 사이클은 터빈 2개, 펌프 1개, 열교환기 4개, 기액분리기 1개, 팽창밸브 1개 등으로 구성되며, 작동유체는 증발잠열이 높은 R717(암모니아)이 사용된다. 그리고 증발기와 응축기 내를 순환하는 작동유체의 증발과 응축을 위해서 고온의 표층수와 저온의 심층수가 각각 사용된다.

Figure 2:

P-h diagram of high-efficiency R717 OTEC power cycle proposed in this study

본 논문에서 제안한 OTEC 발전 사이클의 특징은 냉각기와 기액분리기를 채용하여 응축기의 방출열량을 감소시키고, 재생기를 사용하여 증발기의 흡입열량을 줄이며, 또한 2단 터빈을 사용하여 출력일과 시스템 효율을 증가시키는 것이다.

2.2 성능분석

R717 냉매의 열역학적 물성치와 상태방정식은 HYSYS에서 제공하는 여러 가지 상태방정식 중에서 R717 냉매에 잘 맞는 Peng-Robinson식[12]을 이용하여 계산하였다.

Table 1:

Balance equation of exergy loss(∆exloss) and exergy destruction factor(EDF) for each component of R717 OTEC power cycle proposed in this study

본 시스템의 엑서지 분석에 필요한 식들은 Table 1에 정리하였다. R717용 해양온도차 발전 사이클의 제 2법칙 효율(second law efficiency) η_Ⅱ은 동일한 조건에서 최대 가역 열효율(η_th-rev)에 대한 실제 열효율(η_real)의 비로써, 다음과 같이 정의된다.

여기서, T_H는 히트소스(heat source) 온도이고, T_o는 주위의 온도이다.

R717용 해양온도차 발전 사이클의 열원수(표층수)의 온도(T_ss,in)는 25℃이고, 주위온도(T_o)는 30℃이다. 따라서 식 (1)의 분모항 내에 있는 T_o/T_H값이 1보다 커지게 되므로, 제 2법칙 효율(second law efficiency) ηⅡ은 음수의 값이 나오게 된다. 이러한 경우, 제 2법칙 효율(엑서지 효율)을 계산하는 식은 엑서지 파괴인자(EDF, exergy destruction factor)로부터 구할 수 있다[10].

여기서, EDF_total는 Table 1에서 나타낸 것처럼, 각각의 구성품에 대한 엑서지 파괴인자(EDF)를 모두 합한 값이다.

Table 2에는 본 연구에서 사용되는 R717용 해양온도차 발전 사이클의 성능 분석범위를 나타내었다. Table 2에서 성능 분석범위는 R717용 해양온도차 발전 사이클의 일반적인 운전조건이다. 질량유량(m)은 다른 변수의 운전조건이 기준값일 때 순수일량(W)을 20 kW로 맞춘 값인 1350 kg/h이다. R717용 해양온도차 발전 사이클의 개략도와 상태점을 나타낸 Figure 1과 운전조건을 나타낸 Table 2의 분석범위로부터 Table 1의 수식을 계산하고 이렇게 나온 결과값을 이용하여 R717용 해양온도차 발전 사이클의 제 2법칙 효율에 영향을 미치는 인자들에 대해서 살펴보고자 한다.

3. 결과 및 토론

최고의 OTEC 발전 시스템 효율을 나타내는 중간압력을 찾기 위해서 고단 터빈의 출구 압력(P_H,t,out)을 변화시켜가면서, 증발과 응축열량, 순수일량의 변화를 살펴보았다. 그 결과는 630 kPa에서 최대값(4.25%)을 나타내었다. 따라서 이후의 OTEC 발전 사이클에는 위의 터빈 출구 압력을 적용하여 분석하였다.

Table 2:

Analysis range of high-efficiency R717 OTEC power cycle proposed in this study

3.1 증발기 출구압력의 영향

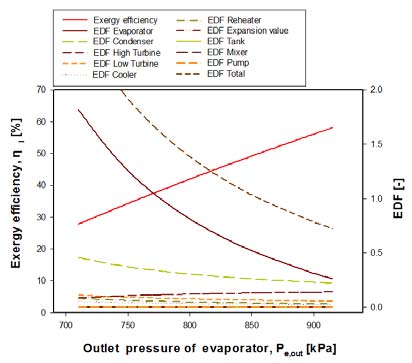
Figure 3은 증발기 출구압력(P_e,out) 변화에 따른 R717용 OTEC 발전 사이클의 엑서지 효율(ηⅡ)과 엑서지 손실인자(EDF)의 변화를 나타낸 것이다. 증발기 출구압력이 증가할수록 엑서지 효율은 약 109% 정도 증가한다. 이는 증발기 출구압력이 증가함에 따라 고단터빈의Figure 3: Exergy efficiency and EDF of R717 OTEC power cycle with outlet pressures of evaporator 입·출구 압력차가 커지고, 결과적으로 고단터빈 일량이 증가하고 순수일량(W)이 증가한다. 그리고 증발기의 EDF_e가 감소하는데, 그 이유는 증발기 출구압력(≒증발온도)이 증가할수록 증발기의 열교환 온도차가 감소해서 증발기의 비가역성이 감소하기 때문이다. 나머지 구성요소의 EDF는 거의 일정하다. 즉, 엑서지 효율을 구하는 식에서 순수일량(W)의 증가와 증발기 EDF^e의 감소에 의해 각 구성기기들의 EDF를 모두 합친 EDF^total이 감소하기 때문에 엑서지 효율은 증가한다.

Figure 3:

Exergy efficiency and EDF of R717 OTEC power cycle with outlet pressures of evaporator

Figure 4:

Exergy efficiency and EDF of R717 OTEC power cycle with outlet pressures of high turbine

Figure 5:

Exergy efficiency and EDF of R717 OTEC power cycle with intlet pressures of condenser

3.2 고단터빈 출구압력의 영향

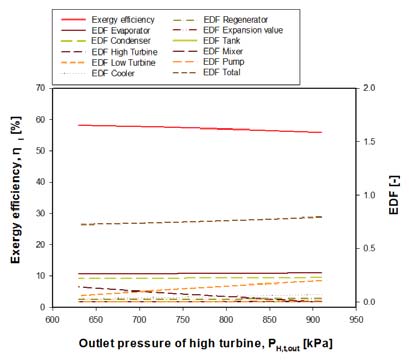
Figure 4는 고단터빈 출구압력(P_H,t,out)의 변화에 따른 R717용 OTEC 발전 사이클의 엑서지 효율(ηⅡ)과 엑서지 손실인자(EDF)의 변화를 나타낸 것이다. 고단터빈 출구압력이 증가할수록 엑서지 효율은 약 4% 정도 감소한다. 이는 식 (2)로부터 각 구성기기의 EDF를 모두 합친 EDF_total이 증가하기 때문이다. 그 이유는 고단터빈 출구압력이 증가할수록 고단터빈의 EDF_H,t는 감소하는 반면, 저단터빈의 EDF_L,t는 증가하는데, 이때 저단터빈의 EDF_L,t 증가량이 약간 더 크다. 그리고 고단터빈 출구압력이 증가할수록 고단터빈의 일량은 줄어들고 저단터빈의 일량은 늘어나게 되는데 이때 고단터빈 일량의 감소가 저단터빈 일량의 감소보다 더 크기 때문에 순수일량(W)은 소폭 감소한다. 결국, EDF_total이 증가하게 되고 엑서지 효율은 감소한다.

3.3 응축기 입구압력의 영향

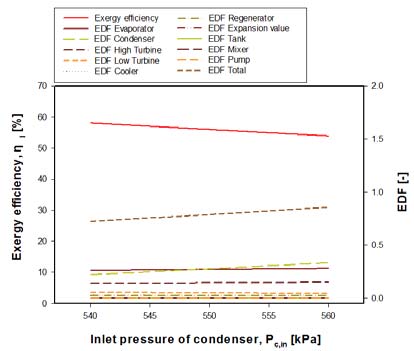
Figure 5는 응축기 입구압력(P_c,in)의 변화에 따른 R717용 OTEC 발전 사이클의 엑서지 효율(ηⅡ)과 엑서지 손실인자(EDF)의 변화를 나타낸 것이다. 응축기 입구압력이 증가할수록 엑서지 효율은 약 8% 정도 감소하는 경향을 보였다. 이는 응축기 입구압력 즉, 저단터빈의 출구압력이 증가하게 되면, 이 저단터빈의 입·출구압력차가 감소하기 때문에 저단터빈 일량이 감소하고, 결과적으로 순수일량(W)이 감소한다. 그리고 응축기의 EDF_c가 감소하게 되는데, 그 이유는 응축기 입구압력(≒응축온도)이 증가할수록 응축기의 열교환 온도차가 증가해서 응축기의 비가역성이 증가하기 때문이다. 나머지 구성요소에 대한 EDF는 거의 일정하다. 즉, 응축기 입구압력이 증가할수록 순수일량(W)이 감소하고 EDF_total이 증가하게 되어 엑서지 효율은 감소한다.

Figure 6:

Exergy efficiency and EDF of R717 OTEC power cycle with outlet vapor qualities of cooler

3.4 냉각기 출구건도의 영향

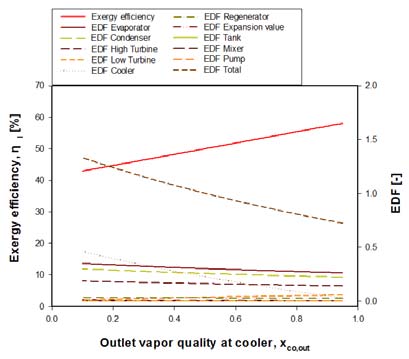
Figure 6은 Table 2의 운전조건에서 냉각기 출구건도(x_HX2,out)의 변화에 따른 R717용 OTEC 발전 사이클의 엑서지 효율(ηⅡ)과 엑서지 손실인자(EDF)의 변화를 나타낸 것이다.

Figure 6에서 알 수 있듯이, 냉각기 출구건도가 증가할수록 엑서지 효율은 약 35% 정도 증가한다. 이는 냉각기의 출구건도가 증가할수록 탱크를 지나 저단터빈으로 들어가는 증기의 양이 많아져서 저단터빈 일량이 증가하게 되므로 순수일량(W)이 증가하게 된다. 즉, 엑서지 효율을 구하는 식에서 순수일량(W)의 증가로 인해 각 구성기기의 EDF를 모두 합친 EDF_total이 감소하기 때문에 엑서지 효율은 감소한다.

4. 결 론

지금까지 본 논문에서 제안한 R717용 OTEC 발전 시스템의 엑서지 효율에 영향을 미치는 증발기 출구압력(P_e,out), 고단터빈 출구압력(P_H,t,out), 냉각기 출구건도(x_HX2,out)와 응축기 입구압력(P_c,in)의 인자들에 대해서 Table 2의 운전조건에서 살펴보았다. 그 결과를 요약하면 다음과 같다.

(1) R717용 OTEC 발전 사이클의 증발기 출구압력, 냉각기 출구건도가 증가할수록 엑서지 효율은 증가한다. 그러나 고단터빈과 응축기 입구압력이 증가할수록 엑서지 효율이 감소한다. 따라서 R717용 OTEC 발전 사이클의 엑서지 효율은 증발기 및 고단터빈 출구압력, 응축기 입구압력과 냉각기 출구건도에 영향을 받는 것을 확인할 수 있었다.

(2) 이러한 작동변수들 중에서 증발기 출구압력(P_e,out)의 변화가 R717용 OTEC 발전 사이클의 엑서지 효율에 가장 크게 영향을 미치고, 고단터빈 출구압력(P_H,t,out)이 가장 적게 영향을 미친다. 따라서 R717용 OTEC 발전 사이클의 엑서지 효율을 증가시키기 위해서는 증발기 출구압력을 증가시키는 것이 가장 유리하다. 즉, 표층수와 열교환하는 냉매의 증발압력(≒증발온도)을 높일 수 있는 증발기 개발이 중요하리라 생각된다. 그리고 본 시스템의 엑서지 효율을 향상시키기 위해서는 반드시 각 구성품의 엑서지 손실을 파악해야 하며 이를 통해 엑서지 손실을 최소화하여 R717용 OTEC 발전 사이클이 최대 효율을 나타낼 수 있도록 해야 한다.

Acknowledgments

본 연구는 국토해양부가 지원하는 ‘해양심층수의 에너지 이용 기술 개발’결과임을 밝히며 연구비 지원에 감사드립니다.

References

J. H. Heo, H. U. Kim, D. I. Yang, C. H. Son, J. I. Yoon, and G. H. Choi, “Performance characteristics of a R744 OTEC power system using high temperature heat source”, The Korean Society of Marine Engineering, p266-267, (2013), (in Korean).
H. S. Lee, H. J. Kim, D. H. Jung, and D. S. Moon, “A study on the improvement for cycle efficiency of closed-type OTEC”, Journal of the Korean Society of Marine Engineering, (2011), 25(1), p80-84, (in Korean). [https://doi.org/10.5916/jkosme.2011.35.1.046]
J. I. Yoon, C. H. Son, S. M. Baek, H. J. Kim, H. S. Lee, “Performance characteristic of R744 OTEC power cycle with operation parameters”, Journal of the Korean Society of Marine Engineering, 36(5), p10-14, (2012), (in Korean). [https://doi.org/10.5916/jkosme.2012.36.5.580]
C. H. Tseng, K. Y. Kao, and J. C. Yang, “Optimal design of a pilot OTEC power plant in Taiwan”, Journal of Energy Resources Technology, 113(4), p294-299, (1991). [https://doi.org/10.1115/1.2905914]
R. H. Yeh, T. Z. Su, M. S. Yang, “Maximum output of an OTEC power plant”, Ocean Engineering, 32(5-6), p685-700, (2005). [https://doi.org/10.1016/j.oceaneng.2004.08.011]
N. J. Kim, C. N. Kim, and W. Chun, “Using the condenser effluent from a nuclear power plant for ocean thermal energy conversion (OTEC)”, International Communications in Heat and Mass Transfer, 36(10), p1008-1013, (2009). [https://doi.org/10.1016/j.icheatmasstransfer.2009.08.001]
T. J. Rabas, C. B. Panchal, and H. C. Stevens, “Integration and optimization of the gas removal system for hybrid-cycle OTEC power plants”, Journal of Solar Energy Engineering, 112(1), p19-28, (1990). [https://doi.org/10.1115/1.2930753]
A. I. Kalina, “Combined cycle system with novel bottoming cycle”, Journal of Engineering for Gas Turbines and Power, 106(4), p737-742, (1984). [https://doi.org/10.1115/1.3239632]
H. Uehara, A. Miyara, Y. Ikegami, and T. Nakaoka, “Performance analysis of an OTEC plant and a desalination plant using an integrated hybrid cycle”, Journal of Solar Energy Engineering, 118(2), p115-122, (1996). [https://doi.org/10.1115/1.2847976]
Z. Shengjun, W. Huaixin, and G. Tao, “Performance comparison and parametric optimization of subscritical organic rankine cycle(ORC) and transcritical power cycle system for low-temperature geothermal power generation”, Applied energy, 88(8), p2740-2754, (2011). [https://doi.org/10.1016/j.apenergy.2011.02.034]
T. Dylan, “Ocean thermal energy conversion: current overview and future outlook”, Renew. Energy, 6(3), p367-373, (1994).
D. Y. Peng, and D. B. Robinson, “A new two-constant equation of state”, Industrial and Engineering Chemistry Fundamentals, 15(1), p59-64, (1976). [https://doi.org/10.1021/i160057a011]
Aspen HYSYS. Version 8.0, Aspen Technology Inc, (2013).