GA 기반의 비선형 PID 제어기 설계 및 CSTR 프로세스에 응용

1. 서 론

선박, 발전소, 석유화학 분야 등에서 운전되고 있는 많은 프로세스들은 강한 비선형성을 보일 뿐만 아니라 시변 특성을 가지고 있다. 특히 석유화학 공정에서 널리 사용되는 연속교반탱크반응기(Continuously Stirred Tank Reactor: CSTR) 내에서 일어나는 화학 반응은 반응물의 농도, 온도, 압력, 촉매, 시간 등에 크게 영향을 받아 비선형성과 시변 특성이 강하고 또 개회로 프로세스에는 불안정한 평형점(Equilibrium point)이 존재할 뿐만 아니라, 경우에 따라서는 불안정한 평형점 부근에서 장시간 운전되어야 할 때가 있다[1][2].

이런 복잡한 프로세스에 기존의 고정 파라미터 제어기를 적용할 때 동작점이 변경되거나 프로세스 파라미터가 변경되면 좋은 성능을 기대할 수 없을 뿐만 아니라 경우에 따라서는 불안정해질 수도 있다. 따라서 제어기 설계 시 보다 정밀하고 안정된 성능을 보장하도록 게인 스케줄링, 적응기법, 신경회로망, 퍼지, 진화기법 등을 접목하는 많은 연구[3]-[6]와 최근에는 표준형 PID 제어기의 프레임상에 다양한 형태의 비선형 함수를 도입한 비선형 PID(Nonlinear PID: NPID) 제어기를 설계하려는 다수의 노력들이 진행되어 왔다[3]-[8].

NPID 제어는 용어상의 의미에서도 짐작할 수 있듯이 그 사용 목적이나 응용 방법에 따라 다양한 형태를 보이고 있지만, 현재까지 발표된 문헌들은 설정치와 출력간의 오차를 비선형적으로 변환해서 PID 제어기에 입력하거나, 아니면 비선형 함수로 표현된 세 이득을 출력의 크기에 따라 변경하는 연구가 주를 이루고 있다[7]-[12].

전자의 연구로 Su 등[7]은 오차에 오차의 구간 제한(Sector-bounded) 함수를 곱해 제어기에 입력하고, 사용된 표준형 PID 제어기의 이득을 Ziegler-Nichols법으로 동조하고, 2자유도 로봇암에 적용하는 방법을 제안하였고, Li 등 [8]은 비선형 추적 미분기(Tracking differentiator)와 비선형조합을 표준형 PID 제어기와 결합하여 미사일의 날개 제어 문제에서 성능을 개선하는데 사용하였다.

한편 후자의 연구로 Zhang et al. [9]는 세 이득을 오차에 대한 하이퍼블릭 시컨트와 지수 함수로 표시한 표준형 PID 제어기를 제안하고 발전기의 여자 제어 시스템에 적용하였고, Korkmaz et al. [10] 또한 가우스 오차 함수(Gaussian error function)로 특정 지워지는 세 비선형 이득을 제안하고 유전알고리즘(GA)으로 파라미터를 동조하는 방법을 제안하였다. So et al. [11]도 마이크로 컨트롤러 상에서 구현이 쉽고 오차와 오차의 변화율에 기초한 비선형함수를 독자적으로 제안하고 GA로 동조한 세 이득을 시변하는 방법을 제안하였다. 이들은 서로 다른 제어 환경에서 나름대로 만족스러운 성과를 제시하고 있으나 더 단순한 함수를 사용하고 또 조정 파라미터 수를 줄이는 등 개선의 여지를 남기고 있다.

따라서 본 연구에서는 기존의 연구들[10]-[12]을 보완하여 단순하면서도 구현이 쉬운 비선형 함수를 도입한 NPID 제어기를 설계하고 GA로 최적 동조하는 문제를 다룬다. 현장에서 흔히 접할 수 있는 포화기를 고려하였고, 이상적인 미분동작의 한계성을 극복하기 위해 필터식을 가진 수정 PID 제어기를 사용한다. 비선형 비례, 적분 및 미분 이득의 파라미터들은 GA를 기반으로 ITAE(Integral of time absolute error) 성능지수를 최소로 하는 관점에서 최적 동조된다. 제안하는 방법은 CSTR 프로세스의 온도 제어에 적용하고 다른 두 방법과 비교하여 그 유효성을 확인한다.

2. 기존의 비선형 제어법

본 연구에서 비교대상으로 사용할 Korkmaz et al. [10]이 제안한 비선형 PID 제어기(이후 Korkmaz NPID 제어기라함)와 Chen et al. [5]이 제안한 적응제어기(이후 Chen 적응 제어기라 함)에 대해 간략히 살펴본다.

3. 제안하는 NPID 제어기

3.1 제안하는 NPID 제어기의 구조

본 연구에서는 표준형 PID 제어기에서 일어날 수 있는 미분폭주 현상을 막도록 식 (7)과 같은 구조의 NPID 제어기를 사용하며, 세 이득은 시변적으로 변경된다.

$\[ C\left(s\right)=K_p\left(e\right)+\frac{K_i\left(e\right)}{s}+\frac{K_d\left(e,\dot{e}\right)s}{1+\frac{T_d\left(e,\dot{e}\right)}{N}s} \]$

(7)

여기서 K_p(e) , K_i(e )와 $$ K_d\left(e, \dot{e}\right)$$는 오차 e 와 오차 변화율 $$ \dot{e}$$의 비선형 함수로서 표준형 PID 제어기의 비례, 적분, 미분 이득과 같은 의미를 가지는 이득이고, $$ T_d\left(e, \dot{e}\right)=K_d\left(e, \dot{e}\right)/K_p\left(e\right)$$는 미분시간이며, N 은 8~20 사이에서 경험적으로 정해지는 상수이고 여기서는 10이 사용된다[13].

3.1.1 비선형 비례이득(Nonlinear proportional gain)

속응성을 높이기 위해 비례동작은 오차가 클 때에는 비례이득을 크게 해줄 필요는 있지만, 응답이 설정치 부근에 도달했을 때에도 계속 큰 값을 유지하면 과도한 동작으로 인해 오버슈트나 진동현상이 일어날 수 있다.

이 점을 고려해 NPID 제어기의 비례이득 K_p(e)는 e 의 크기에 따라 비선형적으로 조절되도록 식 (8)의 함수를 제안한다[12].

$\[ K_p\left(e\right)=a_1+a_{2}f\left(e\right) \]$

(8)

여기서 a₁, a₂는 양의 상수로서 사용자 조정 파라미터이고, f(e )는 구현이 간단하면서 다음과 같이 기술되는 함수이다.

$\[ f\left(e\right)=1-\text{exp}\left(-4e^2\right) \]$

(9)

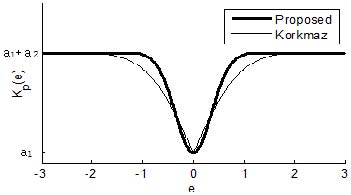
f(e )는 0을 중심으로 e 가 0일 때 0, e 가 커질 때 1에 수렴하는 대칭함수이고, K_p(e)는 a₁, a₂ 값에 따라 그 크기가 결정된다. Figure 1은 식 (2a)와 식 (8)을 그린 것이다.

식 (9)를 선정하게 된 이유는 구현이 쉽고 또 사전 시뮬레이션을 통해 e가 작을 때 비례이득 조정에 적절한 민감성을 보였기 때문이다. 그림에서 보면 e→∞ 이면 K_p(e)들은 상한값 a₁ + a₂에, 반대로 e→0 이면 하한값 a₁에 수렴하는 것을 알 수 있다.

Figure 1:

Kp(e) shapes to changes of e(a1 = 2, a2 = 1)

3.1.2 비선형 적분이득(Nonlinear integral gain)

적분동작은 오차 e의 절대값이 클 때에는 적분이득 값을 줄여 오버슈트 발생에 대비하고, e 의 절대값이 작을 때에는 적분이득 값을 크게 해서 정상상태 오차를 줄이도록 해줄 필요가 있다. 이 점을 고려해 적분이득 K_p(e)는 e 의 크기에 따라 비선형적으로 조절되는 식 (10)을 사용한다[12].

$\[ K_i\left(e\right)=b\left[1-f\left(e\right)\right] \]$

(10)

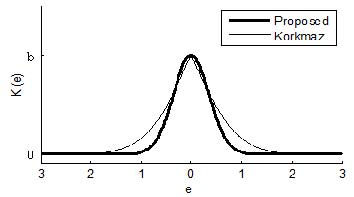
여기서 b(> 0) 또한 사용자에 의해 정해지는 파라미터이고, f(e ) 는 식 (9)에서 정의된 함수이다. Figure 2는 식 (2b)와 식 (10)의 두 K_i(e)를 그린 것이다. 그림에서 보면 e→0이면 K_p(e)는 상한값 b에 수렴하고, 반대로 e→∞이면 하한값 0에 수렴하는 것을 알 수 있다.

Figure 2:

Ki(e) shapes to changes of e(b = 1)

3.1.3 비선형 미분이득(Nonlinear derivative gain)

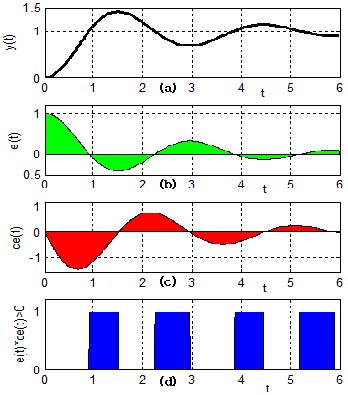
미분동작은 비례동작과 적분동작이 커지면 출력도 같이 커질 것을 예측하고 Figure 3 (c)와 같이 제동을 걸게된다. 전체 제어 사이클 동안 필요 이상의 제동을 걸면 응답속도가 느려지게 되지만, $$ e\dot{e}>0$$인 사이클(Figure 3 (d)의 청색 영역) 동안만 제동을 걸면 비례동작과 적분동작을 더 과감하게 활용할 수 있어서 오버슈트를 줄일 수 있다.

Figure 3:

y, e, e˙ and control cycles when ee˙>0

따라서 미분이득의 크기를 변경하기 위해 다음과 같이 기술되는 시변 함수를 사용한다[12].

$\[ K_d\left(e,\dot{e}\right)=\left\{\begin{array}{c}{\mathrm{c}}_1+c_{2}f\left(e\right), e\dot{e}>0\hfill \\ {\mathrm{c}}_1, elsewhere\hfill \end{array}\right. \]$

(11)

여기서 K_d는 두 매개변수 c₁(>0)와 c₂(> 0)를 가지는 비선형 함수이고, 이 또한 하한값 c₁과 상한값 c₁ + c₂ 사이의 값을 갖는다.

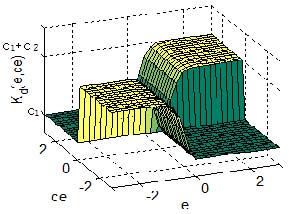
Figure 4는 e 와 $$ \dot{e}$$에 대한 $$ K_d\left(e, \dot{e}\right)$$를 그린 것이다. $$ e\dot{e}>0$$ 인 평면에서 보면 e→0이면 Kde, e˙ 는 c₁에 수렴하고, 반대로 e→∞이면 c₁ + c₂에 수렴하는 것을 확인할 수 있다.

Figure 4:

Kde, e˙ shape to changes of e (c1 = c2 = 1)

3.2 NPID 제어기의 동조

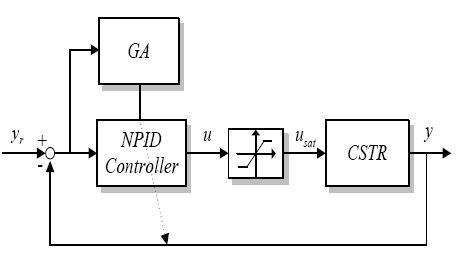
앞서 제안한 NPID 제어기는 총 5개의 파라미터를 가지고 있어 전체 제어 프로세스가 원하는 설정치 추종 성능을 만족하도록 포화기가 포함된 Figure 5에서 동조된다.

Figure 5:

Tuning of the NPID controller with a saturator

동조는 t = 0에서 제어 프로세스가 안정한 평형점에 머물 때 설정치 y_r 를 계단형으로 변경하며 수행되었다.

이때 일어나는 다변수 최적화 문제는 GA [14]를 이용하여 풀며, 성능의 좋고 나쁨을 계량하기 위해 ITAE 성능지수를 사용한다.

$\[ J\left(\varphi \right)={\int }_0^{t_f}t|y_r\left(t\right)-y\left(t\right)|dt \]$

(12)

여기서 φ= [a₁, a₂, b, c₁, c₂ ]^T∈R⁵이고, y_r (t )는 설정치, y(t)는 출력이며, 적분시각 t_f는 이후의 적분값이 무시될 수 있도록 충분히 큰 값이다.

4. 모의실험 및 검토

제안된 방법을 구현해서 모의실험을 실시하고, 그 성능을 Chen 적응제어기 [7]와 Korkmaz NPID 제어기[10]와 비교하였다. Korkmaz NPID 제어기의 경우 비교의 공정성을 유지하기 위해 제안한 NPID 제어기와 동일한 시나리오로 식 (12)를 최소로 하는 관점에서 GA로 동조하였다.

4.1 연속교반탱크반응기(CSTR)

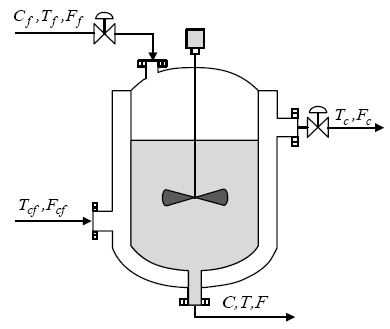
Figure 6은 제어대상으로 사용될 CSTR이고, 여기에는 발열반응이 일어나는 것으로 간주된다. CSTR 내에서 완벽한 반응이 진행되는 최적의 조건을 유지시키기 위해서는 강한 교반과 함께 내부의 온도를 일정하게 유지시킬 필요가 있다. 그림에서 C_f, T_f, F_f와 C , T , F 는 각각 반응물의 입구와 출구 측 농도[mol/m³], 온도[K]와 유량[m³/sec]을 T_cf, F_cf와 T_c, F_c는 각각 냉각수의 입구와 출구 측 온도와 유량을 뜻한다.

Figure 6:

Nonisothermal CSTR process

반응은 반응물에 대하여 1차이고, 교반을 통해 용기 전체를 통해 농도, 온도, 반응속도가 공간적으로 변화가 작은 것으로 간주하면 다음과 같은 무차원화 방정식을 얻을 수 있다[1][2].

$\[ \dot{x_1}=-x_1+D_a\left(1-x_1\right)\text{exp}\left(\frac{x_2}{1+x_2/\gamma }\right)+d_1 \]$

(13a)

$\[ \dot{x_2}=-\left(1+\beta \right)x_2+H{D}_a\left(1-x_1\right)\text{exp}\left(\frac{x_2}{1+x_2/\gamma }\right)+\beta u+d_2 \]$

(13b)

$\[ y=x_2 \]$

(13c)

여기서 x₁과 x₂는 각각 반응물의 농도 C 와 온도 T 를 의미하는 상태변수이고, y와 u는 각각 출력과 입력으로서 반응물의 출구 온도와 냉각수 온도를, d₁과 d₂는 외란을 의미한다. D_a는 Damökhler number, H 는 반응열, β는 열전달계수, V 는 CSTR의 체적, γ = E/RT_f이고 E 는 활성화 에너지와 R 은 기체상수를 의미한다. x₁, x₂, u와 t는 각각 다음 식으로 무차원화 되었다.

$\[ x_1=\frac{C_f-C}{C_f},\mathrm{ }{x}_2=\frac{T-T_f}{T_f}\mathrm{\gamma },\mathrm{ }u=\frac{T_c-T_f}{T_f}\mathrm{\gamma },\mathrm{ }t=t\text{'}\frac{F_f}{V} \]$

(14)

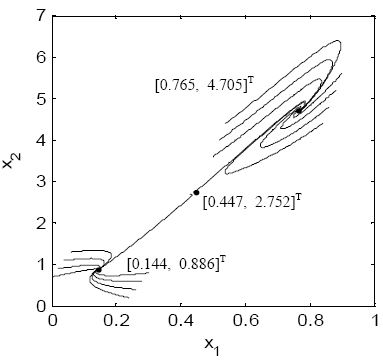
식 (13)의 개회로 시스템은 D_a= 0.072, γ= 20, H = 8, β= 0.3일 때 3개의 평형점 x_eA = [0.144, 0.886]^T, x_eB = [0.447, 2.752]^T, x_eC = [0.765, 4.705]^T을 가지며 그 중 x_eA와 x_eC 는 안정한 평형점, x_eB 는 불안정한 평형점이다. Figure 7은 위상선도 상에 세 평형점을 그린 것이다.

Figure 7:

Phase-portrait for three equilibrium points

CSTR 내의 온도는 냉각자켓을 통해 흐르는 냉각수 양을 가감하여 조절하며, 여기에 사용되는 밸브의 동작은 물리적으로 한계가 있을 수밖에 없다. 따라서 제어기와 CSTR 사이에는 다음 식으로 표시되는 비선형 포화기가 있는 것으로 간주한다.

(15)

4.2 NPID 제어기의 파라미터 동조

모의실험에 사용된 CSTR의 데이터는 D_a= 0.072, γ= 20, H= 8, β= 0.3이고, 샘플링 간격은 0.02로 하였다. GA의 집단크기로는 P_size = 40, 교배확률로는 P_c= 0.9, 동적 돌연변이의 매개변수로는 P_m= 0.05와 b= 4를 사용하였고 [11], NPID 제어기의 파라미터들은 구간 0 < a₁,c₁,b ≦ 60, 0 < a₂,c₂,c ≦ 30에서 탐색되었다. 두 방법의 동조 결과는 Table 1과 같다.

Table 1:

Tuned parameters of the proposed NPID controller and Korkmaz’s NPID controller

4.3 성능 비교

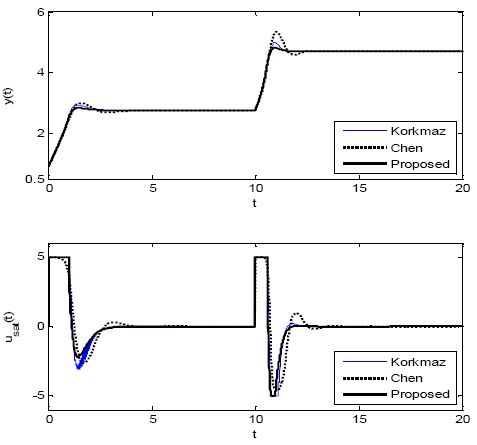
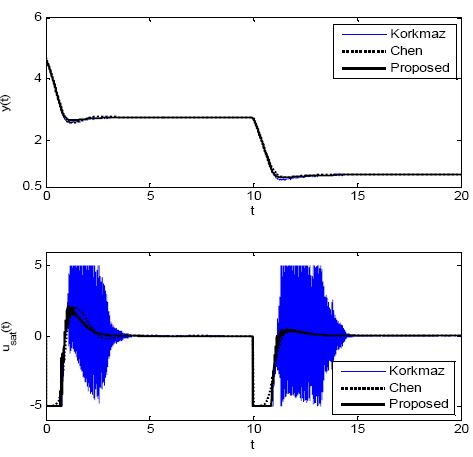
먼저 반응물의 온도를 변경하는 제어 환경을 고려해 설정치 추종 실험을 실시하였다. 실험은 프로세스가 안정한 평형상태 x_eA = [0.144, 0.886]^T에 있을 때 설정치 y_r = 2.752로 계단형으로 증가시켜 불안정한 평형상태 x_eB 로 가져가고, 다시 t= 15에서 y_r = 4.705로 계단형으로 증가시켜 안정한 평형상태 x_eC에 이르는 순서로 하였다. Figure 8은 이때의 출력 y와 포화기 출력 u_sat를 그린 것이다.

Figure 8:

Set-point tracking responses when yr is step-wisely increased from 0.886 to 4.705

그림에서 보면 두 NPID 제어기와 적응 제어기의 응답들은 모두 시간이 경과하면 정상편차 없이 설정치에 도달하지만, 제안한 방법이 두 방법보다 더 작은 오버슈트를 가지고 빨리 접근해 가는 것을 알 수 있다.

Table 2는 세 방법의 정량적인 성능을 보이기 위해 오버슈트(M_p), 도달시간(t_r = t₉₀—t₁₀ ), 2% 정정시간(t_s ), 절대오차의 적분(IAE)를 구한 것이다. 표에서 보면 제안한 방법의 성능이 두 방법보다 앞서는 것을 확인할 수 있다.

Table 2:

Comparison of set-point tracking performances when yr is step-wisely increased from 0.886 to 4.705

CSTR의 내재적인 비선형성으로 설정치를 높일 때와 낮출 때의 응답특성이 서로 다를 수도 있으므로, 이를 확인하기 위해 반대로 프로세스가 평형상태 x_eC = [0.765, 4.705]T에 있을 때 y_r를 2.752로, 다시 x_eB 에 있을 때 t= 15에서 y_r 를 0.886으로 계단형으로 줄이면서 응답을 그린 것이 Figure 9이다. Table 3은 세 방법의 정량적인 성능을 요약한 것이다.

이 경우에도 세 가지 방법 모두 만족스러운 성능으로 설정치를 잘 추종하지만, 특히 Korkmaz NPID 제어기는 비례이득 값이 커질 때 이상적인 미분동작으로 때문에 u_sat에 심한 채터링(Chattering) 현상이 일어나는 것을 볼 수 있다.

Figure 9:

Set-point tracking responses when yr is step-wisely decreased from 4.705 to 0.886

Table 3:

Comparison of set-point tracking performances when yr is step-wisely decreased from 4.705 to 0.886

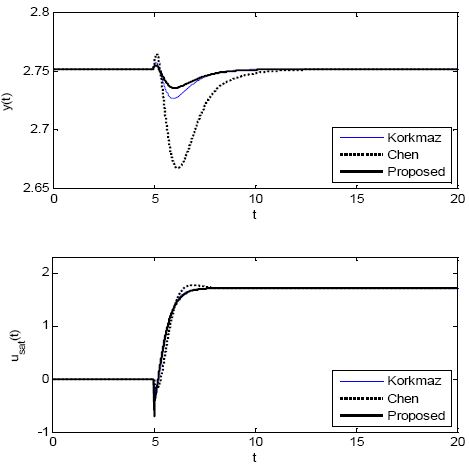
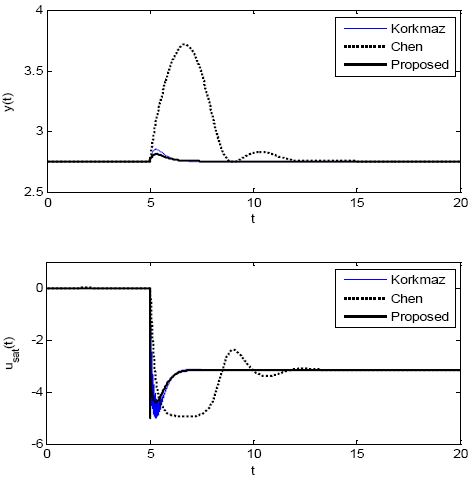
다음은 제안한 방법의 외란 억제 성능을 확인하기 위하여 설정치를 y_r = 2.752에 고정하고 식 (13)의 우측 단에 계단형의 서로 다른 외란 d₁과 d₂를 투입하는 두 가지 시뮬레이션을 실시하였다. 프로세스가 불안정한 평형점 x_eB 에 머물고 있을 때 첫 번째 시뮬레이션은 t= 5 이후 계단형의 외란 d₁= 0.2, d₂= 0.2를, 두 번째 시뮬레이션은 d₁= -0.2, d₂= 0.2를 투입하였다. Figure 10 과 Figure 11은 각각의 시뮬레이션 결과를 그린 것이다.

이 경우에도 제안한 방법은 효과적으로 외란을 억제하고 있지만, 반면에 나머지 두 방법은 외란에 의한 응답 변동이 크면서 회복시간이 길고, 적응제어기의 성능이 제일 좋지 못한 것을 알 수 있다.

다시 세 방법의 성능을 정량적으로 계량하기 위하여 응답변동의 피크치(Perturbance peak) M_peak와 외란의 영향이 소멸되고 출력이 설정치로 회복되는데 걸리는 회복시간(Recovery time) t_rcy를 구하였다. 이때 M_peak = |y_r - y_max | 또는 |y_r - y_min | 를 의미하고, t_rcy는 출력 y가 설정치 y_r의 2% 이내로 회복되는데 걸리는 시간을 의미한다. Table 4에서 보면 제안한 방법의 성능이 전반적으로 우수함을 확인할 수 있다. 특히 두 방법은 M_peak도 클 뿐 아니라 t_rcy도 긴 것을 알 수 있다.

Figure 10:

Disturbance rejection responses when d1 and d2 are step-wisely changed while yr = 2.75(d1=d2 = 0.2)

Figure 11:

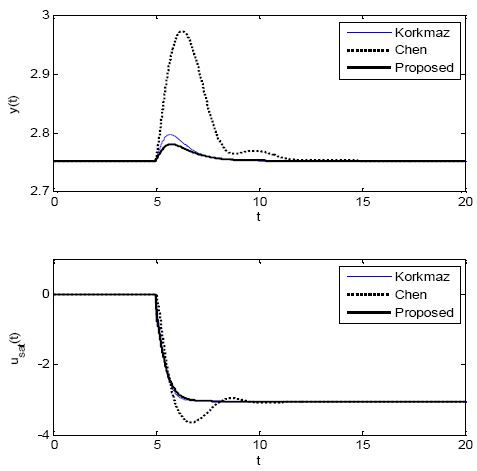
Disturbance rejection responses when d1 and d2 are step-wisely changed while yr = 2.75(d1= -0.2, d2= 0.2)

Table 4:

Comparison of disturbance rejection performances when d1and d2 are step-wisely changed.

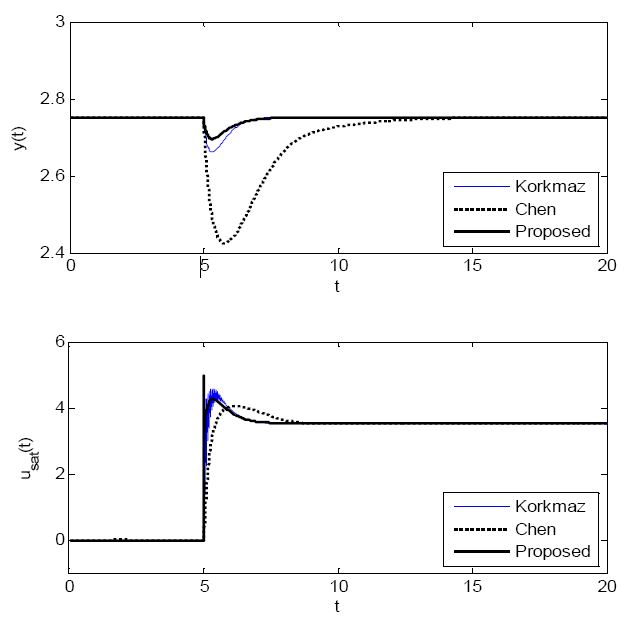
CSTR 내의 화학반응은 시간을 두고 일어나므로 파라미터 변동에 대한 제안한 방법의 강인성을 확인하기 위해 두 가지 시뮬레이션을 실시하였다. Figure 12는 제어 프로세스가 x_eB 에 머물고 있을 때 t= 5이후 파라미터 D_a를 0.072에서 0.09로 H 를 8에서 9로 동시에 변경하며 얻은 결과이고, Figure 13은 t= 5 이후 D_a를 0.072에서 0.05로, H 를 8에서 7로 동시에 변경하며 얻은 응답을 그린 것이다.

Figure 12:

Responses comparison to parameter changes (Da = 0.072→0.09, H = 8 → 9)

그림에서 보면 두 NPID 제어기는 파라미터 변동에 덜 민감한데 비해, 적응제어기는 피크값이 크고 또 회복시간도 길어, 전반적으로 만족스럽지 못함을 알 수 있다. 이는 정량적인 결과를 보여주는 Table 5에서도 확인할 수 있다.

앞에서도 간단히 언급하였지만 Korkmaz NPID 제어기는 매 루프마다 erf(e ) 함수를 수치적분해야 하므로, 이를 마이크로 컨트롤러에서 구현하게 될 경우에는 계산 부담으로 작용할 수 있다.

이를 확인하기 위해 두 방법간의 연산시간을 PC(Intel Core(TM)2 Duo CPU 3.00GHz)와 MATLAB 환경에서 비교하였다. 두 방법 다 세 이득을 연산하는 알고리즘만 선별해서 500회 반복 수행하고 이때 걸린 시간을 평균하였다. Table 6은 이를 요약한 결과이다. 표에서 보면 본 방법이 Korkmaz법 보다 약 100배나 빨리 연산되는 것을 확인할 수 있다.

Figure 13:

Responses comparison to parameter changes(Da = 0.072→0.05, H = 8→7)

Table 5:

Comparison of robustness to step-wisely parameter changes

Table 6:

Comparison of computation time

이상의 시뮬레이션 결과를 토대로 제안된 방법이 설정치 추종과 외란 억제에 더 효과적이며 또 파라미터 변동에도 강인함을 알 수 있었다.

5. 결 론

본 연구에서는 시변 이득을 가지는 비선형 PID 제어기를 제안하고, 세 비례, 적분, 미분 이득은 오차와 오차 변화율의 함수로서 간단하면서도 구현이 쉬운 비선형 함수로 기술하였다. 산업 현장에서 자주 접하게 되는 포화기를 고려하였고, 필터식을 가진 NPID 제어기의 파라미터들은 GA를 기반으로 ITAE 평가함수를 최소로 하는 관점에서 최적 동조되었다. 제안된 방법을 CSTR 프로세스의 온도를 제어하는 문제에 적용하였고. 그 성능을 검정하기 위해 Korkmaz NPID 제어기와 Chen 적응제어기의 성능과 비교한 결과 제어 성능이 향상되었음을 확인할 수 있었다. 차후 안티와인드업기법을 결합하는 연구가 필요하다고 사료된다.

Acknowledgments

본 연구는 석사학위논문(“Temperature Control of a CSTR Using a Nonlinear PID Controller”, 한국해양대학교 해양과학기술전문대학원)을 개선한 것입니다.

References

• W. H. Ray, Advanced Process Control, McGraw-Hill Book Co., N.Y., (1981).
• J. P. Corriou, Process Control: Theory and Applications, Springer-Verlag, London, (2004). [https://doi.org/10.1007/978-1-4471-3848-8]
• U. S. Banu, and G. Uma, “Fuzzy gain scheduled CSTR with GA-based PID”, Chemical Engineering Communications, 195(10), p1213-1226, (2008). [https://doi.org/10.1080/00986440801907003]
• M. A. Nekoui, M. A. Khameneh, and M. H. Kazemi, “Optimal design of PID controller for a CSTR system using particle swarm optimization (PSO)”, Proceedings of the 14th International Power Electronics and Motion Control Conference, EPE-PEMC 2010, Ohrid, Republic of Macedonia, pT7-63-T7-66, (2010).
• C. T. Chen, and S. T. Peng, “Learning control of process systems with hard input constraints”, Journal of Process Control, 9, p151-160, (1999). [https://doi.org/10.1016/S0959-1524(98)00038-9]
• L. S. Saoud, F. Rahmoune, V. Tourtchine, and K. Baddari, “An inexpensive embedded electronic continuous stirred tank reactor (CSTR) based on neural networks”, Proceedings of the International Conference on Multimedia Technology (ICMT), China, p6233-6237, (2011). [https://doi.org/10.1109/icmt.2011.6002445]
• Y. X. Su, D. Sun, and B. Y. Duan, “Design of an enhanced nonlinear PID controller”, Mechatronics, 15, p1005-1024, (2005). [https://doi.org/10.1016/j.mechatronics.2005.03.003]
• C. Li, S. Wang, Z. Yue, J. Yu, and H. Wang, “Anti-windup nonlinear PID controller design and its application to winged missile control system”, Proceedings of the 27th Chinese Control Conference, p377-379, (2008).
• H. Zhang, and B. Hu, “The application of nonlinear PID controller in generator excitation system”, Energy Procedia, 17, p202-207, (2012). [https://doi.org/10.1016/j.egypro.2012.02.084]
• M. Korkmaz, Ӧ. Aydoğdu, and H. Doğan, “Design and performance comparison of variable parameter nonlinear PID controller and genetic algorithm based PID controller”, Proceedings of the 2012 IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Trabzon, p1-5, (2012). [https://doi.org/10.1109/INISTA.2012.6246935]
• G. So, M. So, and G. Jin, (2013), “EA-based design of a nonlinear PID controller”, Proceedings of the 37th KOSME Spring Conference, p374, (in Korean).
• J. Lee, Temperature Control of a CSTR Using a Nonlinear PID Controller, M.S. Thesis, Department of Convergence Study on the Ocean Science and Technology, School of Ocean Science and Technology, Korea Maritime and Ocean University, (2015).
• K. J. Åström, and T. Hägglund, PID Controllers: Theory, Design and Tuning, ISA Press, (1995).
• G. Jin, Genetic Algorithms and Their Applications, Kyowoo Publishing Co., (2000).