유체항력 계산을 통한 자율무인잠수정의 운동성능 예측과 실험

1. 서 론

최근 해양자원 개발, 해양환경 탐사 및 해양 구난활동 지원에 필요한 무인잠수정(UUV)에 대한 관심이 증가하고 있다. UUV(unmanned underwater vehicle) 는 보통 ROV(remotely operated vehicle)과 AUV(autonomous underwater vehicle)로 분류된다. ROV는 모선과 연결된 통신케이블을 사용하여 운용하지만 AUV는 탑재된 전원과 컴퓨터 및 센서를 이용하여 독립적으로 자신의 위치를 인지하고 내장된 경로추적 알고리즘을 이용하여 주어진 임무를 수행하는 자율성을 가져야 한다[1]-[3].

군사용으로서의 AUV는 수중에 설치되어 있는 기뢰탐색 및 작전지역의 해양지형 조사, 적 잠수함 탐지 및 추적 등의 용도로 개발되고 있다[4][5]. 국내에서도 한국해양연구원을 중심으로 AUV에 대한 초기 연구개발이 진행된 바 있다[6]. AUV는 내부공간의 한계로 인해 탑재된 배터리의 운용시간이 제한된다는 단점이 있으며, 잠항 시에는 모선과의 교신이 불가능하므로 정확한 수중위치 인식 및 장애물에 대한 회피거동 등 자율적인 수중운동에 필요한 수중센서, 제어기 및 자율성 알고리즘에 대한 연구가 계속되어야 할 것이다.

본 연구에서는 AUV의 수중 운동성능에 영향을 미치는 선체의 유체항력 계수를 설계단계에서 산출하고, 이를 포함한 동역학 모델을 사용하여 AUV의 수중운동을 예측하는 시뮬레이션 연구를 수행하였으며, 시험을 통해 이를 부분적으로 검증하는 연구를 수행하였다.

2. AUV의 외부형상 및 제원

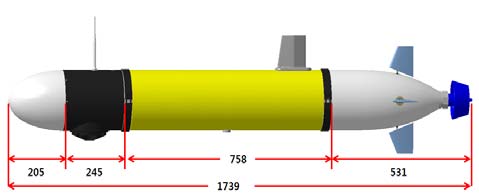
본 연구의 AUV 모델에서 사용한 AUV의 선체는 크게 선수부, 중앙부, 선미부의 3부분으로 나뉘며 외형 및 치수는 Figure 1과 같다. AUV의 중량은 43 kgf이며 부력은 약 44 kgf이다. 선수부와 선미부의 형상은 Myring Profile을 적용하였고, 선체의 개략제원은 Table 1에 나타내었다. AUV의 운동은 1개의 추진기와 4개의 방향타에 의해서 이루어지며, 방향타는 익형의 미국표준규격인 NACA0012를 적용하였다.

Figure 1:

The dimension of AUV

Table 1:

Specifications of AUV

3. AUV의 동역학 모델

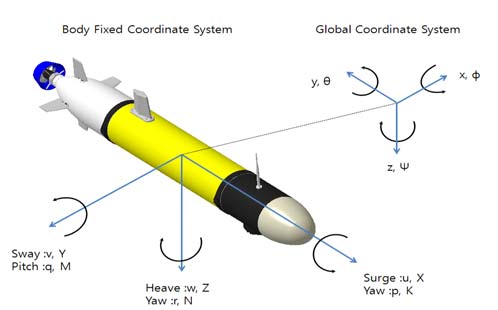
6자유도를 가지는 AUV의 위치와 자세를 나타내기 위해 전역 좌표계의 원점은 AUV가 출발하는 해수면 상의 한 지점을 기준으로 정의하고, 물체 고정 좌표계는 그 중심이 AUV의 부력중심과 일치하도록 정의하여 Figure 2에 나타내었다.

Figure 2:

Coordinate system of AUV

일반적으로 6자유도를 가지는 수중 운동체는 12개의 상태 변수를 사용하여 비선형 운동방정식으로 나타낼 수 있다. 선체의 부력중심에 정의된 물체 고정 좌표계를 기준으로 x-z평면과 x-y평면에 대해서 선체형상을 대칭으로 근사화 할 수 있다. 본 연구에서 사용한 AUV는 거의 대칭형이므로 관성적 (Ixy, Iyz, Ixz)이 주관성모멘트(Ixx, Iyy, Izz)에 비해 매우 작기 때문에 무시하였다. 관성적을 무시한 6자유도 운동방정식은 다음식과 같다.

식 (1)에서 우변의 항들은 AUV에 작용하는 부력과 중력 차이에 의한 정수력(hydrostatic force), 동수력감쇠(hydrodynamic damping), 부가질량(added mass), 방향타와 추진기에 의한 힘과 모멘트로 정의되며 다음식과 같이 구성된다[7].

4. AUV의 유체항력계수의 계산

본 연구에서는 정수력(hydrostatic force), 부가질량(added mass), 방향타력과 추진력은 이론식[8]을 이용하여 계산하였으며, 항력으로 정의되는 동수력감쇠(hydrodynamic damping)는 ANSYS-CFX을 사용하여 CFD 해석을 통해 구하였다[9].

4.1 전방향 항력

전방향(axial flow)항력은 AUV의 진행방향에 대해서 발생하는 선체의 유체저항을 의미한다. 항력계수를 구하기 위해 전방향의 투영면적 형상은 Figure 3과 같다.

Figure 3:

Projected area of the front of AUV

CFD해석을 수행하기에 앞서 요소격자분할작업이 필요하다. 유체영역에서 복잡한 구조물의 형상을 해석하는데 적합한 격자로 4면체요소와 피라미드요소를 사용하였으며, 선체와 유체 사이의 경계층을 표현하기 위해 프리즘요소를 사용하였다. 수행된 요소격자분할은 Figure 4와 같이 나타내어진다. 유동해석을 위해 선체를 감싸는 유체영역을 정의해야 하는데, 이러한 유체영역은 선체 주위의 유동에 영향을 미치지 않을 정도의 적절한 크기로 설정하여야 한다. ANSYS-CFX에서 권장하는 SST(Shear Stress Transport)모델을 사용하여 비선형적인 유동을 해석하였다.

Figure 4:

Element mesh of the AUV

CFD 해석에 사용된 데이터를 정리하면 Table 2와 같다.

Table 2:

CFD analysis data

Table 3은 0.8, 1.0, 1.2, 1.4, 1.6 m/s의 5개 운항속도에 대하여 AUV에 발생하는 항력과 항력계수 값을 계산하고 평균값을 구하였다.

Table 3:

Axial flow drag force and coefficient of the AUV

4.2 횡방향 항력

횡방향(cross flow)항력은 선체의 측면에 대한 항력을 의미한다. 항력계수를 구하기 위해 횡방향의 투영면적 형상은 Figure 5와 같다.

횡방향 항력은 앞서 구한 전방향 항력(axial flow)에 대한 방법과 마찬가지로 계산되어진다. 각각 0.2, 0.4, 0.6, 0.8 m/s 의 운항속도에서 AUV에 발생하는 항력과 항력계수 값을 Table 4에 나타내었다.

Figure 5:

projected area of the side of AUV

Table 4:

Cross flow drag force and coefficient of AUV

4.3 항력 검증시험

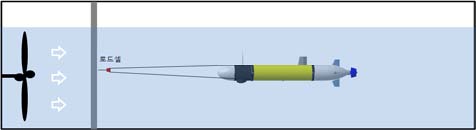
항력시험은 국립수산과학원의 회류수조에서 실시하였으며, 측정방법과 관련된 개념은 Figure 6과 같다. 수조의 왼쪽에 있는 대형 프로펠러가 일정 유속을 만들어내면 인장형 로드셀이 AUV에 묶여 있는 줄에 발생하는 장력을 측정하는 방식으로 진행되었다. Figure 7은 실제 시험하는 장면을 나타내고 있다.

Figure 6:

Concepts of the drag force measurement

Figure 7:

Measurement of the drag force of AUV

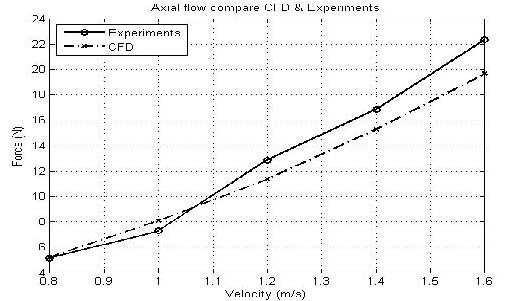
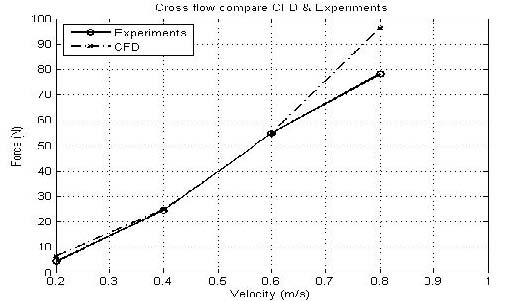
CFD해석과 시험의 결과 값을 전방향(axial flow)과 횡방향(cross flow)에 대해 비교하여 각각 Figure 8 과 9에 나타내었다. CFD에 의해 계산된 값과 시험에 의해 측정된 값들이 유사한 경향을 보이는 것을 알 수 있으며, CFD를 이용한 항력계산이 유효함을 알 수 있다.

Figure 8:

Comparison between the CFD and measured values for axial flow drag forces

Figure 9:

Comparison between the CFD and measured values for cross flow drag forces

5. AUV 운동제어기 설계

실제 무인 잠수정의 특성은 선형 관성력 계수, 선형 감쇠계수, 비선형 감쇠계수 등을 모두 고려한 정밀한 수학적 모델링을 바탕으로 제어기가 설계되면 좀 더 정확한 제어를 수행할 수 있다. 하지만 비선형 감쇠계수의 경우 조종 성능에 미치는 영향이 미미하다고 알려져 있고, 실제 많이 사용하고 있는 PD제어기를 적용하기 위해 비선형 계수들은 무시하였다. 제어기는 수평면과 수직면 운동으로 분리하여 설계하였고 3차원 수중공간에서 AUV의 운동시뮬레이션을 수행하였다.

5.1 PD제어기

5.1.1수평면 제어기

6자유도 운동방정식에서 수평면 상에서 0의 값을 가지는 커플링 성분, 방향타에 의한 성분, 2차 이상의 고차항 성분을 선형화하면 식 (4)와 같이 선형화 모델로 간략화 할 수 있다.

$\[ \left(I_{zz}-N_{\dot{r}}\right)\dot{r}=N_{r}r+{N_{\delta }}_r{\mathrm{\delta }}_{\mathrm{r}} \]$

(4)

앞서 구한 유체항력 계수 값을 식 (4)에 대입하여 행렬식으로 표현하면 식 (5)와 같다.

$\[ \begin{array}{c}\left[\begin{array}{c}\dot{r}\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{cc}-0.1127& 0\\ 1& 0\end{array}\right]\left[\begin{array}{c}r\\ \psi \end{array}\right]+\left[\begin{array}{c}-0.2033\\ 0\end{array}\right]{\delta }_r\hfill \\ y=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}r\\ \psi \end{array}\right]\hfill \end{array} \]$

(5)

식 (5)의 시스템에 PD 제어기를 사용하여 폐루프 전달함수를 구하면 식 (6)과 같다.

$\[ G\left(s\right)=\frac{-0.2033\left(K_p+K_{d}s\right)}{s^2+\left(0.1127-0.2033K_d\right)s-0.2033K_p} \]$

(6)

시스템의 비례게인(K_p) 값과 미분상수(K_d) 값은 MATLAB Simulink를 이용하여 시행착오적인 반복계산에 의해 구하였으며 K_p 값은 -2, K_d 값은 –4를 얻었다.

5.1.2 수직면 제어기

수평면 제어기와 마찬가지로 수직면에 대한 선형화 모델로 간략화 하면 식 (7)과 같다.

$\[ \begin{array}{c}\left(I_{yy}+M_{\dot{q}}\right)\dot{q}=M_{q}q-z_{G}W\theta +M_{{\delta }_s}{\delta }_s\hfill \\ \dot{z}=-U\theta \hfill \\ q=\dot{\theta }\hfill \end{array} \]$

(7)

유체항력 계수 값을 식 (7)에 대입하여 행렬식으로 표현하면 식 (8)과 같다.

$\[ \begin{array}{c}\left[\begin{array}{c}\dot{q}\\ \dot{\theta }\\ \dot{z}\end{array}\right]=\left[\begin{array}{ccc}-0.1135& -0.1399& 0\\ 1& 0& 0\\ 0& -1& 0\end{array}\right]\left[\begin{array}{c}q\\ \theta \\ z\end{array}\right]+\left[\begin{array}{c}-0.2032\\ 0\\ 0\end{array}\right]\left[{\delta }_s\right]\hfill \\ y=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\left[\begin{array}{c}q\\ \theta \\ z\end{array}\right]\hfill \end{array} \]$

(8)

식 (8)에 PD 제어기를 사용한 폐루프 전달함수는 식 (9)와같다.

$\[ G_{depth}\left(S\right)=\frac{0.2032K_{zp}}{s^3+\left(0.1135-0.2032K_d\right)S^2+\left(0.1399-0.2032K_p\right)s+0.2032K_{zp}} \]$

(9)

깊이제어기에서도 Matlab Simulink를 사용하여 시행착오 반복에 의해 비례게인(K_p)은 4, 미분게인(K_d)은 5, 그리고 깊이제어게인(K_zp)은 1.7을 얻었다.

5.2 AUV 운동시뮬레이션

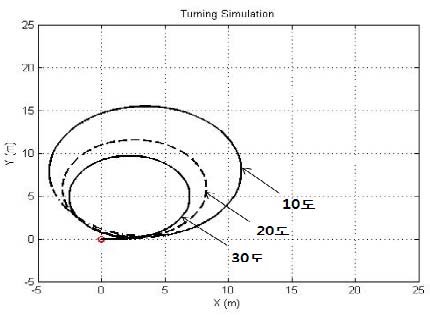
우선 수평면 상에서 고정하여 선회운동 시뮬레이션을 함으로써 AUV 모델의 기본적인 타당성을 검토하였다. Figure 10에서 방향타 각이 10도, 20도, 30도인 경우 선회반경은 각각 약 5 m, 6 m 및 7.5 m가 됨을 알 수 있다. 속도는 1 m/s로 고정하였다.

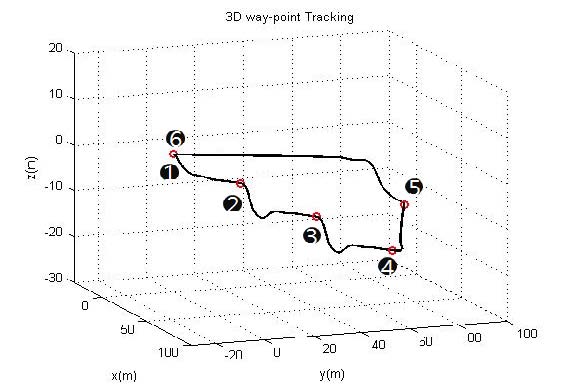
AUV의 속도를 1 m/s로 고정하고 수평 및 깊이 제어기를 사용하여 3차원 공간상에 주어진 경유점(way-point)들을 통과하는 운동시뮬레이션을 수행하였다. 그 결과는 Figure 11과 같이 모든 경유점(way-point)들을 잘 추종함을 예측하였다. 외란은 없다고 간주하였다.

Figure 10:

Circular turning simulation

Figure 11:

3D Way-point tracking simulation

6. 시뮬레이션과 시험 값 비교

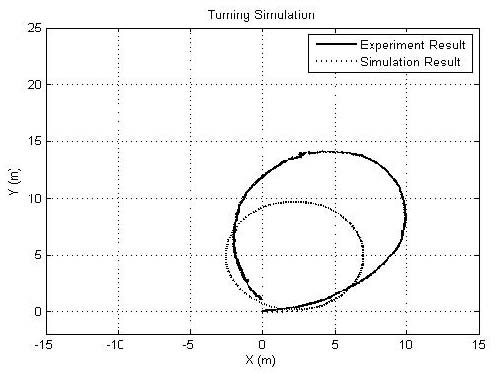
시뮬레이션을 통해 확인한 AUV의 운동성능을 검증하기 위해 실해역 시험을 수행하였다. Figure 12과 같이 수평면상에서 AUV의 방향타 각을 30도로 고정하여 제어기 없이 선회반경 시험을 하였으며, 시뮬레이션 결과와 시험 결과를 비교하여 나타내었다. 시뮬레이션에서의 선회반경은 약 5 m이었는데 실해역에서의 선회반경은 약 7.5 m의 타원형을 나타내고 있다. 이는 수치모델과 AUV 시제품의 동적 파라메터 오차 또는 조류에 의한 외란의 영향으로 판단된다.

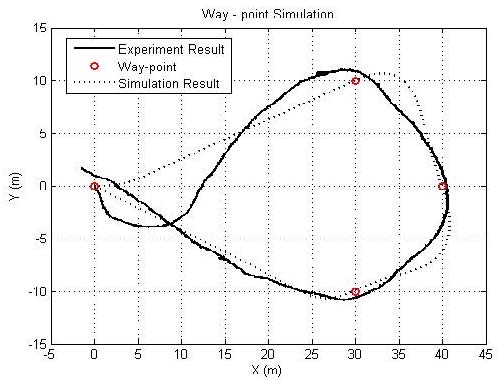
Figure 13은 수평면 상에서 서로 10 m 이상 떨어진 경유점(way-point)들을 설정하여 각 경유점들을 통과하여 돌아오는 수상운동 시뮬레이션과 실해역 운항시험 결과를 비교한 것이다. 실해역 시험에서는 AUV의 초기방향을 인위적으로 네 번째 경유점과 시계방향으로 직각이 되도록 위치시켰는데도 이를 극복하고 이후 경로를 비교적 잘 추종하고 있음을 보여주고 있다.

Figure 12:

Circular turning test

Figure 13:

Way-point tracking test

7. 결 론

본 연구는 AUV의 개발에 사용되는 동역학모델에 대한 연구이다. 선체의 유체저항 계수를 이론식과 CFD를 이용하여 계산하였고 동역학모델을 완성하였다. AUV의 수중운동 시뮬레이션에는 PD제어기를 적용하였고, Matlab Simulink를 사용하여 게인값들을 도출하였다. 동역학 모델과 PD제어기를 사용하여 3차원 경유점들을 추종하는 수중운동 시뮬레이션을 통해 운동성능을 예측하였다.

유체항력 및 수중운동시뮬레이션 결과를 검증하기 위해 수조시험과 실해역 시험을 실시하였다. 30도의 최대 방향타각을 적용한 고정 선회운동 시뮬레이션의 경우 약 5 m의 선회반경을 가지는 것으로 예측되었으나 실해역에서는 약 7.5 m의 선회반경을 가지는 것으로 나타났다. 이는 선회운동의 경우 전방향과 횡방향 항력계수가 융합될 뿐만 아니라 롤운동이 연성되는 특성이 본 모델에 포함되지 않아 오차로 나타난 것으로 판단되며 또한 실해역 시험에서는 일정방향의 조류로 인해 타원운동으로 나타난 것으로 판단된다. 경유점들을 통과하는 실해역 운항시험의 경우는 시뮬레이션 결과와 유사하게 원활한 경로추적성능을 보임을 알 수 있었다. 본 연구에서 본 바와 같이 AUV의 개발 단계에서 해석이론 및 CFD를 활용하여 계산한 유체항력계수 값을 이용하면 선체의 운동을 비교적 정확하게 예측할 수 있다고 판단된다. 물론 AUV의 최종 개발단계에서는 보다 다양한 시험을 통한 운동성능 검증이 필요할 것이다.

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(2014년)에 의하여 연구되었음.

References

• P. M. Lee, “Development of an advance deep-sea unmanned underwater vehicle (1)”, Korea Ocean Research & Development Institute, (2007), (in Korean).
• B. H. Jun, P. M. Lee, and Y. K. Lim, (2009), “Trends in the cruising-type AUVs technologies”, Journal of the Korean Society for Precision Engineering, 26(5), p14-22, (2009).
• S. C. Yu, (2009), “Introduction to specific purpose AUV and Applications”, Journal of the Korean Society for Precision Engineering, 26(5), p33-40, (2009).
• B. Anderson, and J. Crowell, “Workhorse AUV - A cost-sensible new Autonomous Underwater Vehicle for Surveys/Soundings, Search & Rescue, and Research”, (2005).
• R. P. Stokey, and A. Roup, “Development of the REMUS 600 Autonomous Underwater Vehicle”, Jane's Underwater Security Systems and Technology, (2009).
• F. Y. Lee, B. H. Jun, and P. M. Lee, “Implementation and test of ISIMI100 AUV for a member of AUVs Fleet”, OCEANS 2008, (2008).
• F. M. White, Fluid Mechanics 6th Edition, McGraw-Hill Korea, p608-609, (2007).
• T. Prestero, Verification of a Six-Degree of Freedom Simulation Model for the REMUS Autonomous Underwater Vehicle, M.S. thesis, MIT/WHOI, (2001).
• “ANSYS CFX-Basic”, Release 12.0.
• T. H. Joung, K. Sammut, F. He, and S. K. Lee, “A study on the motion analysis and design optimization of a ducted type AUV by using CFD analysis”, Journal of Ocean Engineering and Technology, 23(1), p48-53, (2009).