A Numerical Study on the Performance of a Two-Stage Ejector-Diffuser System
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The conventional ejector-diffuser system makes use of high pressure primary stream to propel the secondary stream through pure shear action for the purposes of transport or compression of fluid. It has been widely used in many industrial applications such as seawater desalination, solar refrigeration, marine engineering, etc. The present study is performed numerically to study the performance of a two-stage ejector-diffuser system. The detailed flow phenomenon of the ejector-diffuser system has been critically predicted by means of the numerical approach using compressible Reynolds averaged Navier–Stokes (RANS) equations. The axi-symmetric supersonic ejector-diffuser flow has been solved by a fully implicit finite volume scheme with a two-equation k-omega turbulence model. The numerical results are validated with existing experimental data. Detailed flow physics and their contributions on ejector performance are detected to compare both single-stage and two-stage ejectors. The performance improvement on the ejector-diffuser system is discussed in terms of the mass flux ratio and the coefficient of power.
Keywords:
Fluid transportation, Compressible flow, Supersonic flow, Shock wave, Ejector-diffuser system1. Introduction
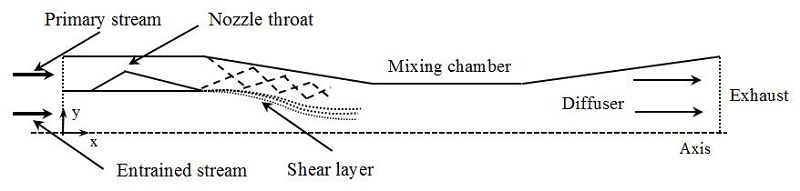
The primary stream of the ejector-diffuser system flows out from the supersonic nozzle with high pressure and high kinetic energy to entrain the secondary stream into the mixing chamber due to the strong shear actions. Two streams are completely mixed in the chamber and exhaust through a diffuser, where their pressure is increased to meet the back pressure located at the surrounding of the ejector exit. Many researching works have been done to increase the performance of the ejector [1]-[4], but results were still unsatisfactory due to its complicated turbulent mixing, compressibility effects and even flow unsteadiness inside the ejector-diffuser system.
Compared with other industrial machineries, the ejector-diffuser system has a fatal drawback that its efficiency is relatively low [5][6]. One of the important reasons is the momentum consume during the mixed flow discharging process. Since the high Mach number primary flow is mixed with the secondary flow inside the mixing chamber, the mixed streams are still carrying high momentum until flowing out the ejector. For most industrial applications where an ejector-diffuser system is installed, the ejector exit is usually connected to a pressure tank where the flow momentum is almost wasted.
In the past decades, many researches have been performed to utilize the ignored momentum dissipation [7]-[9]. One effective method is to introduce the second ejector-diffuser system to utilize the momentum of the mixed flow [10]-[12]. G. Giuseppe. et al. [10] numerically investigated the geometrical effects on the ejector pressure recovery performance in a two-stage ejector refrigeration plant. A two-stage steam ejector was studied with annular primary flow at the second stage. Results revealed the maximum COP at given external inlet fluid temperatures as a function of mass flows, dimensions and temperature differences in the heat exchangers. Singhal et al. [11] installed a two-stage ejector in the chemical lasers for its pressure improvement. A general treatment on the design of a profiled ejector for the case of dissimilar motive and suction fluids that are typical of these lasers. The results revealed the increase in recovery ratio for various conditions of entrainment ratio over the conventional ejectors. At the same time, Gamisans et al. [12] studied the single- and two-stage ejector for its application in venturi scrubber. The results showed a strong influence of the liquid scrubbing flow rate on pollutant removal efficiency. The use of a two-stage venturi tube considerably improved the absorption efficiency.
The objective of present study is to come up with an efficient method for better utilization of the discharged momentum of the ejector-diffuser system. In the present study, the internal flows of the single-stage and two-stage ejector have been numerically simulated by commercial software using RANS equations. The ratio of mass flux and coefficient of power is introduced to explore the performance improvement of the two-stage ejector-diffuser system. Initial results of mass flux ratio are declaring the benefit of the two-stage configuration on ejector performance. The operating pressures are normalized by back pressure of the ejector. The comparison of mass flux ratio among different mixing chamber dimension clearly demonstrates the geometrical effects on the performance improvement of the ejector-diffuser system.
2. Numerical Analysis
2.1 Computational model
A single-stage supersonic ejector-diffuser system with an annular primary stream inlet is shown in the Figure 1. The supersonic primary flow is capable of propelling the secondary stream into the mixing chamber due to the strong shear actions, which appears as the shear layer shown in the Figure 1. The interaction between the primary flow and entrained flow leads to a series of shock waves which decelerate the primary flow and result in high energy loss subsequently. In the meantime, the mixed flow containing high momentum exhausts from the ejector exit which is normally connected to an condensation chamber, where this momentum is wasted mostly. Thus, the objective of present study is to come up with an efficient method for better utilization of the discharged momentum.
The introduction of a two-stage ejector-diffuser system can be a favourable configuration to utilize the remaining momentum of the mixed flow and increase the energy utilization rate considerably. The schematics of the two-stage supersonic ejector-diffuser system geometry used in the present study were shown in the Figure 2. The inlet of the second stage ejector was connected with the exit of the first stage ejector. Thus the mixed flow of the upper stream can be considered to be the secondary flow of the second stage ejector. The primary flow inlet of the second stage was installed at the periphery of the ejector, thus its position can be corresponded to the first primary flow inlet.
2.2 Numerical method
Pressure inlet boundary condition was set at primary inlets of the ejector, for both single-stage and two-stage ones. The secondary inlet and outlet of ejector were extended to stabilize the computational results. Pressure outlet boundary conditions with atmospheric pressure were used at both secondary inlet and outlet of the ejector. Therefore, the secondary stream inlet and ejector exit were propelled and exhausted freely.
For the CFD software, ANSYS Fluent 14.0 was chosen to simulate internal flows of ejector. Ideal gas was used as the working fluid in all cases. A finite volume scheme and density- based solver with coupled scheme were applied in the computational process. SST k-ω turbulent model, implicit formulations were used considering the accuracy and stability. Second-order upwind scheme was used for turbulent kinetic energy as well as spatial discretizations. The flow is governed by the two-dimensional, compressible, steady-state form of the fluid flow conservation equations. Reynolds Averaged compressible Navier–Stokes (RANS) equations are used in this work, which are more suitable for variable density flows. The governing equations can be written as following:
Continuity:
| (1) |
where, ρ represents density and ui,j,k represents the velocity components in the scale of meter per second.
Momentum:
| (2) |
In which the velocity is given as the mass-averaged values. where t represents the time, p represents the pressure, μ is the viscosity and the last term indicates the Reynolds-stress tensor.
The modelled energy equation:
| (3) |
Where the energy E and temperature T are representing the mass-averaged values. In this equation, Cp is the specific heat, Prt represents the turbulent Prandtl number and the last term is the effective stress tensor.
The shear-stress transport (SST) k-ω model can effectively blend the robust and accurately calculate the turbulence kinetic energy (k) and the specific dissipation rate (ω). The form can be obtained from these equations:
| (4) |
and
| (5) |
In these equations, Ğk represents the generate on of turbulence kinetic energy due to mean velocity gradients. Gω represents the generation of ω. Γω and Γω represent the effective diffusivity of k and ω, respectively, which are calculated as described below. Yk and Yω represent the dissipation of k and ω due to turbulence, calculated as described in Modeling the Turbulence Dissipation. Dω represents the cross-diffusion term while Sk and Sω are user-defined source terms.
The effective diffusivities for the SST k-ω model are given by:
| (6) |
and
| (7) |
where σk and σω are the turbulent Prandtl numbers for k and ω, respectively. The turbulent viscosity, μt, is computed as follows:
| (8) |
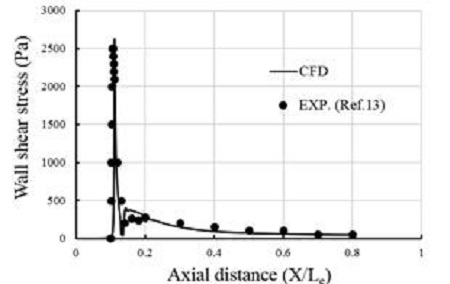
A two-dimensional symmetric model was applied in the present works. Commercial software Gambit was used in the present research to create mesh domain. A structure mesh was employed in this case for ejector and quadrilateral cells were used in the mesh creation. Boundary layer effects were considered by making finer grid densely clustered close to the walls. The first (coarse) grid with y+ of about 1.7 has 458,250 cells. The second (medium) grid set has 668,525 cells with a y+ of about 1.2. The third (fine) set grid is generated using the same minimum space as the second set has 896,220 cells. The computational domain with 668,525 cells was chosen because of its less computational time and more accurate result. The validation was performed to compare the CFD results with experimental data [13]. The wall shear stress along the axis was used to validate the present study, as shown in the Figure 3. The difference between CFD analysis and experimental results was less than 2.5%. In the Figure 3, Le represents the total length of the first-stage ejector diffuser system.
3. Results and Discussion
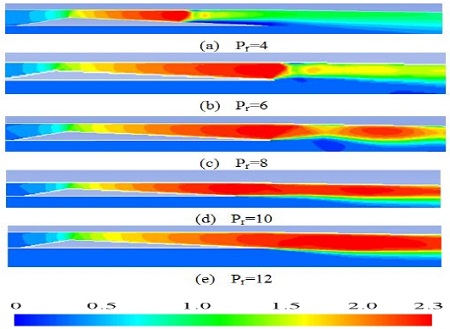
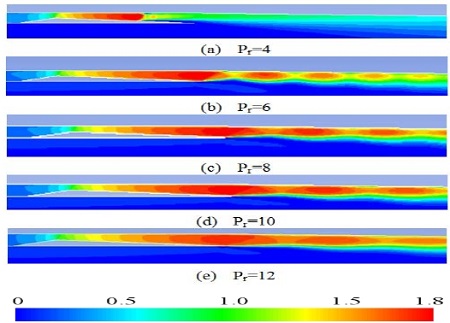
In the present study, the Mach number contours near the primary nozzle exit for both first-stage and second-stage ejectors has been plotted in the Figure 4 and 5. For both figures, the Mach number contours at different pressure ratio (Pr) were compared from each other. The pressure ratios were defined by the ratio of the total pressure at the primary flow inlet to the back pressure of the ejector-diffuser system.
The Mach number contours of the primary inlet flow of the first stage ejector-diffuser system has been shown in the Figure 4. It can be clearly found that the Mach number distribution, shock waves and shock strength are totally different from each other. Along with the pressure ratio increases, the shock wave strength also increases. It is interesting to observe that, the shock is moving downstream the primary nozzle flow, as the Pr increases. It is because the total pressure at the primary flow inlet increases and thus the nozzle pressure ratio (NPR) is also increased. After the primary stream flows out from the primary nozzle exit, the Mach number is rapidly decreased due to its mixing process with the secondary entrained stream.
Figure 5 represents the Mach number contours of the primary inlet flow of the second stage ejector-diffuser system. The difference between first stage nozzle and second stage nozzle can be obviously obtained after comparing with the Figure 4. At the same pressure ratio, the shock strength of the first stage primary flow seems stronger than that of the second stage primary flow. That is because the secondary flow of the second stage ejector is generated by the mixed flow of the first stage ejector, where the ejector exit is located. Thus the back pressure of the second stage ejector is higher than the first stage ejector. At a same pressure ratio, the actual pressure ratio of the second stage ejector is lower than that of the first stage ejector.
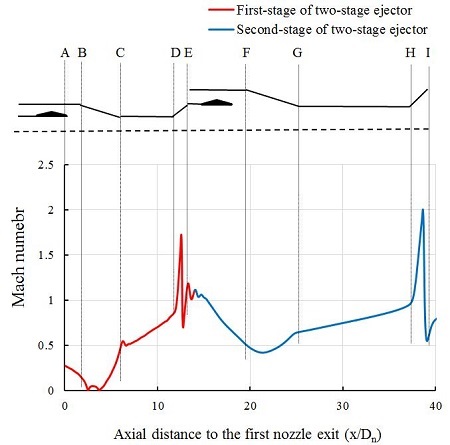
Similar results can be also obtained from Figure 6 and 7, where the Mach number and static pressure distribution along the two-stage ejector axis were plotted. Figure 6 represents the Mach number distribution along the two-stage ejector axis. From A-B, the Mach is decreasing due to the mixing effects between primary stream and entrained stream. Then the mixed flow is increased to supersonic during the converging section and the constant area of the mixing chamber. Since the mixed flow gets diffuser of the system, a series of shock waves happen due to the low back pressure. The Mach number finally achieves one at the exit of the first stage ejector, where the flow is chocked at this position. After the mixed flow from first ejector flows into the second stage ejector, the mixed flow meets the second primary flow and thus again mixed at E-F. After the supersonic is generated in the second mixing chamber, the shock wave inside second diffuser seems stronger than that in the first diffuser. While the number of shock waves are decreased in the second stage ejector.
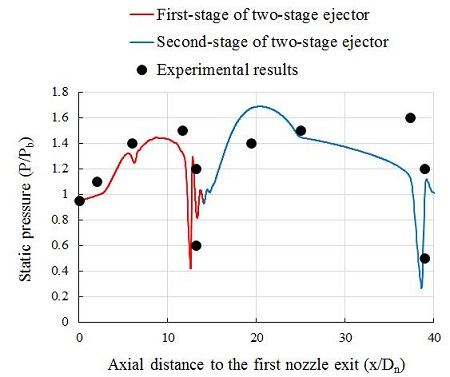
The static pressure distribution along the two-stage ejector axis can be found in the Figure 7. The distribution can be similarly explained by the same mixing process as mentioned above. The numerical results were also compared with the experimental data in this figure, the small difference indicates the accuracy of the present study.
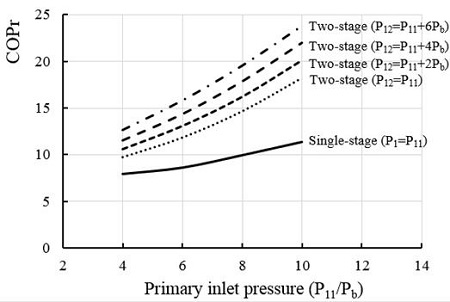
The performance improvement of the two-stage ejector- diffuser system is summarized in the Figure 8, in terms of its effects on the coefficient of power (COPr). The coefficient of power (COPr) is defined by the following equation:
| (9) |
where the subscript 2 indicates the secondary entrained flow, the subscripts 11 and 12 indicate the first primary stream and secondary primary stream, respectively. In this equation, local mass flux (m), enthalpy (h), temperature (T), pressure (P) and inlet area (A) are employed to calculate the coefficient of power. The COPr is capable of calculating all the input heat, but also involving the kinetic energy of all the inflows. Initial results of COPr are shown in the Figure 8, declaring the benefit of the two-stage configuration on ejector performance. The operating pressures were normalized by back pressure of the ejector. The comparison of COPr of two-stage and single-stage ejector clearly demonstrates the effects of the former model on the performance improvement of the ejector-diffuser system. It is also known that as the second primary stream pressure increases, its effects on COPr improvement appears more remarkably.
4. Conclusions
The present numerical study is carried out to study the performance of the two-stage ejector-diffuser system. Compressible Reynolds averaged Navier–Stokes equations are solved by numerical approaches coupled with a two-equation turbulence model. Compare to the single-stage ejector- diffuser system, the two-stage model obtains higher entrained mass flux at a same pressure ratio. The coefficient of power represents that higher energy saving is obtained for the two-stage ejector-diffuser system. The Mach number and static pressure distribution of the first stage and second stage ejectors are compared to study the detailed flow physics of the updated geometry. The two-stage ejector-diffuser system is proved to be an efficient tool to utilize the extra momentum of the mixed flow of the first stage ejector. Further work is going on to optimize the two-stage ejector-diffuser system.
Acknowledgments
This work was supported by Advanced Research Center Program (No. 2013073861) through the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) contracted through Next Generation Space Propulsion Research Center at Seoul National University.
This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2014), held at Paradise Hotel, Busan, Korea on September 17-19, 2014.
References
-
Y. M. Chen, and C. Y. Sun, “Experimental study of the performance characteristics of a steam-ejector refrigeration system”, Experimental Thermal and Fluid Science, 15(4), p384-394, (1997).
[https://doi.org/10.1016/S0894-1777(97)00006-X]

-
Z. Aidoun, and Ouzzane, M., “The effect of operating conditions on the performance of a supersonic ejector for refrigeration”, International Journal of Refrigeration, 27(8), p974-984, (2004).
[https://doi.org/10.1016/j.ijrefrig.2004.05.006]

-
V. Lijo, H. D. Kim, S. Matsuo, and T. Setoguchi, “A study of the supersonic ejector-diffuser system with an inlet orifice”, Aerospace Science and Technology, 23(1), p321-329, (2011).
[https://doi.org/10.1016/j.ast.2011.08.009]

-
X. Yang, X. Long, X. Yao, “Numerical investigation on the mixing process in a stream ejector with different nozzle structures”, International Journal of Thermal Sciences, 56, p95-106, (2012).
[https://doi.org/10.1016/j.ijthermalsci.2012.01.021]

- D. V. Manoha, Desalination of Seawater using a High-Efficiency Jet Ejector, M.S. Thesis, Department of Chemical Engineering, Texas A&M University, (2005).
- W. Somsak, CFD Optimization Study of High-Efficiency Jet Ejector, Doctoral Dissertation, Department of Chemical Engineering, Texas A&M University, (2008).
-
M. N. Biswas, and A. K. Mitra, “Momentum transfer in horizontal multi-jet liquid-gas ejector”, The Canadian Journal of Chemical Engineering, 59(5), p634-637, (1981).
[https://doi.org/10.1002/cjce.5450590513]

-
K. Pianthonga, W. Seehanama, M. Behniab, T. Sriveerakula, and S. Aphornratana, “Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique”, Energy Conversion and Management, 48(9), p2556-2564, (2007).
[https://doi.org/10.1016/j.enconman.2007.03.021]

-
F. S. Kong, H. D. Kim, Y. Z. Jin, T. Setoguchi, “Computational analysis of mixing guide vane effects on performance of the supersonic ejector-diffuser system”, Open Journal of Fluid Dynamics, 2(3), p45-55, (2012).
[https://doi.org/10.4236/ojfd.2012.23005]

-
G. Gr. zzini, and R. Andrea, “Numerical optimisation of a two-stage ejector refrigeration plant”, International Journal of Refrigeration, 25(5), p621-633, (2002).
[https://doi.org/10.1016/S0140-7007(01)00063-9]

-
G. Singhal, A. L. Dawar, and P. M. V. Subbarao, “Application of profiled ejector in chemical lasers”, Applied Thermal Engineering, 28(11), p1333-1341, (2008).
[https://doi.org/10.1016/j.applthermaleng.2007.10.009]

-
X. Gamisans, S. Montserrrat, and F. J. Lafuente, “Gas pollutants removal in a single-and two-stage ejector–venturi scrubber”, Journal of Hazardous Materials, 90(3), p251-266, (2002).
[https://doi.org/10.1016/S0304-3894(01)00352-1]

-
G. Singhala, R. Rajesha, Mainuddina, R. K. Tyagia, A. L. Dawara, P. M. V. Subbaraob, and M. Endo, “Two-stage ejector based pressure recovery system for small scale SCOIL”, Experimental Thermal and Fluid Science, 30(5), p415-426, (2006).
[https://doi.org/10.1016/j.expthermflusci.2005.09.002]