Characteristics of the propulsion shafting alignment for a small class electric propulsion ship equipped with a reduction gear
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In response to the International Maritime Organization’s (IMO) strengthened marine environmental regulations and the trend of high oil prices, newly built ships are increasingly adopting eco-friendly technologies. Large vessels engaged in international navigation typically employ dual-fuel diesel engines based on low-carbon or zero-carbon fuels, while small vessels operating mainly in coastal waters utilize electric propulsion systems powered by batteries. To optimize the performance of propellers, which are more efficient at low rotational speeds, these systems often incorporate reduction gears. The integration of reduction gears necessitates careful shaft alignment to prevent quality issues such as misalignment-induced bearing damage. While classification societies generally do not mandate shaft alignment analysis for propeller shafts with diameters under 400 mm, they recommend evaluating the bearing reaction forces of reduction gear shafts during the design phase to ensure reliability.
This study investigates the static and dynamic alignment characteristics of propulsion shafting systems equipped with reduction gears in small electric propulsion vessels. Key findings highlight the impact of dynamic loads on bearing reaction forces and the need for adjustments to maintain alignment under varying conditions. An optimal alignment configuration is proposed to enhance design stability, thereby contributing to safer and more efficient propulsion systems for small vessels.
Keywords:
Propulsion shafting system, Electric propulsion ship, Reduction gear, Shaft alignment analysis1. Introduction
With the International Maritime Organization's (hereafter IMO) reinforced marine environmental regulations and the prolonged era of high fuel prices, newly constructed ships are increasingly required to adopt eco-friendly technologies that can reduce greenhouse gas emissions. Large ships engaged primarily in international navigation are adopting dual-fuel diesel engines using low-carbon or zero-carbon fuels [1], while small ships operating in coastal waters are employing electric propulsion systems based on electric batteries [2][4].
Electric propulsion systems offer significant advantages, including high torque at low loads, improved propulsion efficiency, reduced fuel costs, and lower maintenance expenses, making them highly advantageous in reducing vessel operating costs. However, to optimize the characteristics of propellers, which achieve higher efficiency at lower rotational speeds, a reduction gearbox must be installed.
From the perspective of shaft alignment, propulsion shafting systems equipped with reduction gearboxes require more precise shaft alignment than traditional propulsion systems where the engine and propeller are directly connected. During operation, the torque generated by the propulsion engine is converted according to the reduction ratio and transmitted at high torque with low rotational speed. This torque is delivered through the gear teeth of the reduction gearbox. Poor alignment of the gear wheel shaft can lead to excessive gear tooth loads, causing reduced safety margins and potential damage such as pitting [5].
Generally, for the propeller shaft with a diameter of 300mm or less, international classification societies do not require the shaft alignment analysis. However, for propulsion shafting systems with reduction gearboxes, it is recommended to evaluate the reaction forces on the bearings supporting the gearbox shafts during the design phase to prevent quality issues arising from misalignment [6].
The issue of shaft bearing damage caused by misalignment in propulsion shaft systems was first observed in U.S. Navy vessels in the 1950s. Since then, active research by shipyards and classification societies has led to the development of shaft alignment analysis methods applicable to ships [7][11]. Recent shaft alignment problems have predominantly occurred in large and high-powered vessels due to increased rigidity of the propulsion shafts, often resulting in damage to the afterward stern tube bearings. Consequently, classification society regulations on propulsion shafting systems primarily focus on the safe design of stern tube bearings [12].
In contrast, smaller vessels, such as passenger ships, work-boats, and small cargo vessels operating in coastal waters, commonly employ high-speed engines or electric motors for propulsion, necessitating the use of reduction gearboxes. These vessels typically use single-stage gear reduction gearboxes, with propeller shaft diameters designed to be less than 400mm. As a result, shaft alignment analysis is not mandated, and the shaft installation is typically conducted in a straight configuration.
Sun et al. performed a shaft alignment analysis on a 500-ton high-speed patrol vessel, demonstrating that misaligned shafts posed more significant issues at the fore bearings of the reduction gearbox than at the aft bearings. They emphasized the need for propulsion shaft analysis considering the stiffness of stern tube bearings to ensure the stability of the reduction gearbox [12]. Kim et al. compared the flexibility characteristics of shaft systems with twin stern tube bearings supporting the propeller shaft and evaluated changes in flexibility and transverse vibration characteristics in a 50,000-ton product tanker with a single stern tube bearing. Furthermore, they analyzed the effects of intermediate bearing placement on shaft alignment and transverse vibration to propose an optimal shaft system layout that avoids transverse vibration resonance and ensures shaft flexibility in ships equipped with single stern tube bearings [13].
This study focuses on the shaft alignment analysis of small electric propulsion vessels equipped with reduction gearboxes, examining the alignment characteristics influenced by the application of reduction gearboxes. Based on the results, this paper proposes an optimal propulsion shaft system layout that incorporates static and dynamic loads of the reduction gearbox and the characteristics of gear shaft support bearings, thereby enhancing the design stability of propulsion shaft systems.
2. Methodology for the Shaft Alignment Analysis
2.1 Theoretical basis for the shaft alignment analysis
Several theoretical approaches are available for analyzing bearing reaction forces in the shaft alignment, including the three-moment method, transfer matrix method, and matrix structural analysis method (finite element method) [5]-[6][10][14]-[16]. In this study, the matrix structural analysis method, which is widely used for analyzing complex structures, was employed.
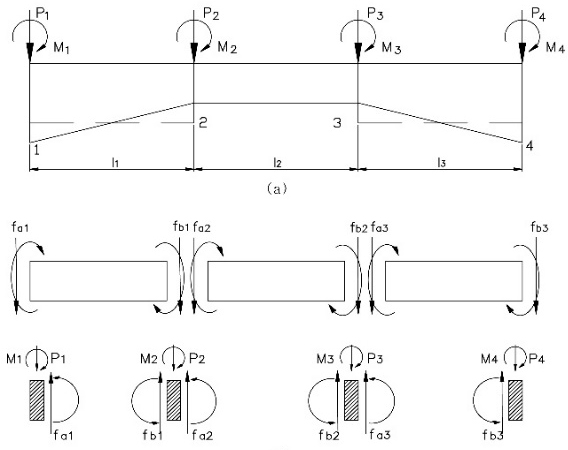
In general, the shafting system can be considered as a non-uniform beam subjected to lateral loads and moments. As illustrated in Figure. 1, the beam is discretized into infinitesimal segments. For each segment, the stiffness matrix, external force vector, and other properties are computed. By applying the beam's nodal equations, the relationship for the system is expressed as shown in Equation (1).
| (1) |
The first vector on the right-hand side represents the external forces acting on the nodes, while the second vector collects the fixed-end sectional forces of each element, where the intermediate forces acting on the elements are converted into nodal loads. The coefficient matrix on the left-hand side corresponds to the global stiffness matrix of the entire beam. By solving Equation (1) for UP1 to UP4, the displacements at each node can be determined. To simplify, Equation (1) can be expressed as Equation (2). Rearranging by transposing the sectional force vector f to the left-hand side yields Equation (3).
| (2) |
| (3) |
Here, the inverse of the stiffness matrix K is referred to as the flexibility matrix. Multiplying both sides of Equation (3) by the flexibility matrix yields Equation (4). Using Equation (4), the displacements at each node can be calculated. Since the reaction forces at the support bearings are considered external forces, they are included in the P term. By substituting the results from Equation (4) into Equation (3), the unknown reaction forces at the specified points can be determined.
| (4) |
Additionally, the reaction influence coefficient represents the change in support loads (reaction forces) at each bearing due to the vertical movement of an adjacent bearing by 1.0 mm. In other words, lowering the height of one bearing increases the load on the adjacent bearings, and this process continues until the changes become negligible. This indicates that every bearing in the system exhibits a load influence coefficient when its height is either lowered or raised by a unit amount. Therefore, a large influence coefficient signifies that the shaft system is highly sensitive to alignment errors. The relationship between the reaction forces and the influence coefficients can be expressed using the concept of a matrix, as shown in Equation (5).
| (5) |
Therefore, the state analysis of the shaft system involves dividing the shaft system into a finite number of arbitrary elements and calculating the stiffness matrix for each element. These matrices are then combined to construct the global stiffness matrix for the entire shaft system. Next, the load at each point is calculated by displacing each bearing position downward by a unit height (1 mm), and the differences between these values and the baseline height (where all bearings are maintained at the same level) are used to calculate the Reaction Influence Number (hereafter RIN). Using these influence coefficients, the bearing loads for various changes in bearing height are calculated, and the optimal heights that keep these loads within allowable limits are determined. Additionally, the bending moments and shear forces at each node are computed, and the resulting stresses are evaluated.
2.2 Alignment Analysis for the Propulsion Shafting System
This section examines the boundary conditions and factors influencing the analysis to simplify the complex shaft system considered during propulsion shaft alignment.
The reference line for propulsion shaft alignment is defined as the point passing through the center of the aft stern tube bearing, which is the closest to the propeller. For low-draft vessels, such as the one in this study, the reference point is set at the aft strut bearing (or Y-strut bearing). Additionally, the line connecting the center points of the Y-thrust bearing and the stern tube bearing (or I-strut bearing) is used as the reference line.
For the reaction support points of the bearings, the aft stern tube bearing, which is the closest to the propeller, has different effective support points depending on the static or dynamic state. In the static state, the effective support point is assumed to be at L/4 from the aft end of the Y-strut bearing, while in the dynamic state, it is assumed to be at L/3 from the aft end of the Y-strut bearing. For all other bearings, the effective support point is set at L/2. Here, L represents the length of the bearing.
The support stiffness of the bearings is assumed to be infinite. The shaft deflection and bearing offset are considered positive (+) when positioned above the reference line, while external forces are considered positive (+) when acting downward from above the reference line. Additionally, the hydrodynamic load of the propeller is considered to generate a positive (+) moment when it rotates in a direction that lifts the aft end of the propeller upward.
Table 1 presents the fundamental material properties applied for the propulsion shaft alignment analysis, while Tables 2 and 3 show the external forces acting on the propulsion shaft system of the studied vessel. The propeller weight is considered as an external force in the static state, with its value varying depending on the degree of submersion. In the dynamic state, the propeller hydrodynamic forces are accounted for, based on DNV classification society standards [17].
Table 4 presents the criteria for the alignment analysis of the propulsion shafting system. Upon review, it is observed that the pressure on the aft stern tube bearing, based on the projected area of the white metal bearing, must not exceed 0.8 MPa under any circumstances [5,17]. However, for the research vessel, Thordon bearings are used, and the manufacturer's recommended limit of 0.55 MPa is applied. Similarly, for the roller bearings supporting the gearbox shaft, the manufacturer's recommended values are also adopted [18]-[19].
3. Analysis Results and Discussion
Figure 2 illustrates the general arrangement of the vessel under study, while Table 5 provides the specifications of the propulsion shafting system. Upon review, the vessel adopts a 320 kW large electric motor as its propulsion engine, with a single-stage reduction gearbox (reduction ratio: 4.95) installed at the rear of the propulsion motor. The propeller achieves maximum output at 361.6 rpm through the reduction gearbox. The propeller has four blades with a diameter of 1.6 m and a total weight of 245 kg, including the propeller cap. The propeller shaft has a diameter ranging from 125 mm to 130 mm and a length of 5,805 mm. Additionally, the intermediate shaft has a diameter of 110 mm and a length of 900 mm.
The types of bearings supporting the propulsion shafting system are as follows: the propeller shaft is supported by the Y-strut bearing and the stern tube bearing, both of which are Thordon bearings based on seawater lubrication. The gearwheel shaft of the reduction gearbox is equipped with tapered roller bearings, which are designed to withstand both axial and radial loads simultaneously.
3.1 Analysis Results of the Shaft Alignment in a Straight Shaft Condition
Figure 3 and Tables 6-9 present the analysis results of the shaft alignment in a straight configuration. In this analysis, the propulsion shafting system is assumed to be supported with infinite stiffness. Upon review, it is observed that the load on all bearings in the static state is below the standard values specified by the classification society. However, the reaction force of the forward-side bearing of the reduction gear shows a negative value(-). Additionally, when the propeller bending moment acts below the reference line, the load on the forward bearing of the reduction gearbox is as low as 22.7 N. In the design stage of the propulsion shafting system, it is essential to ensure that the reaction forces of all supporting bearings are positive (+). However, in the case of the research vessel, the negative (-) reaction force of the forward bearing of the reduction gearbox indicates that the shaft system's arrangement may not be optimal. Regarding the shaft bending moment, when the propeller bending moment acts below the reference line, the maximum bending moment of 2,757.7 Nm occurs at the Y-strut bearing. This is because the Y-strut bearing is the closest support to the heavy propeller.
The analysis of the Reaction Influence Number (hereafter RIN) for each bearing indicates that the RIN value in the dynamic condition is 2.8% higher than in the static condition. This difference is attributed to the change in the effective support point of the Y-strut bearing, which shifts forward when the propulsion shafting system transitions to a dynamic condition. For small vessels, such as the one studied, the propeller shaft typically has a small diameter and low shaft stiffness. Due to these characteristics, the propulsion shafting systems of small vessels often do not carry out the shaft alignment analysis during the design stage and are commonly installed in a straight configuration. However, for the shafting systems with reduction gearboxes, the short spacing between the bearings supporting the gearwheel shaft results in a high RIN, leading to a significantly low reaction force at the forward bearing of the reduction gearbox. Therefore, measures must be implemented to increase the reaction force at the forward bearing of the reduction gearbox.
3.2 Analysis Results of the Shaft Alignment in a Fair Curve Shaft Condition
When the diameter of the propeller shaft is less than 300 mm, the propulsion shafting system is typically installed in a straight shaft condition. However, in cases where a reduction gearbox is present, the reaction force at the forward bearing of the gearbox approaches "0." Therefore, it is necessary to adjust the offsets of the forward and aft bearings of the gearbox to increase the reaction force at the forward bearing.
Figure 4 and Tables 10 and 11 present the results of shaft alignment analysis in a fair curve shaft condition. In this analysis, the propulsion shafting system is assumed to be supported with infinite stiffness. To increase the reaction force at the forward bearing of the reduction gearbox, the offset of the forward bearing is adjusted to -0.38 mm, and the offset of the aft bearing is adjusted to -0.35 mm. Here, the "-" sign indicates that the bearing height is lowered relative to the reference line. Upon review, it is observed that, in the static condition, the reaction force at the forward bearing of the gearbox slightly decreases due to the buoyancy effect on the propeller. However, the reaction forces at the forward and aft bearings of the gearbox are evenly distributed.
In the dynamic condition, the external forces acting on the gearwheel of the reduction gearbox tend to increase the load on the gearbox bearings. When the propeller bending moment acts below the reference line, the load on the aft bearing of the reduction gearbox increases significantly to 8,195.8N. Conversely, when the propeller bending moment acts above the reference line, the load on the forward bearing of the reduction gearbox rises sharply to 5,267.4 N. This behavior is attributed to the short spacing between the bearings supporting the gearwheel shaft of the reduction gearbox, resulting in a high Reaction Influence Number and a pronounced effect of external forces on the shafting system in the dynamic condition. Regarding the bending moment of the shaft, the largest bending moment, 2,262.0 Nm, occurs at the Y-strut bearing when the propeller bending moment acts below the reference line. Notably, when the propeller bending moment acts above the reference line, a bending moment of -200 Nm is observed at the gear shaft near the forward bearing of the reduction gearbox. In conclusion, for the propulsion shafting systems of small vessels equipped with reduction gearboxes, it is appropriate to adjust the offsets of the forward and aft bearings of the reduction gearbox to positions below the reference line to ensure that the load on the forward bearing remains positive.
4. Conclusion
This study investigated the alignment characteristics of propulsion shafting systems in small electric propulsion vessels equipped with reduction gearboxes. And then optimal measures is proposed to enhance design stability of the shafting system by reflecting the static and dynamic loads of the reduction gearbox and the characteristics of its support bearings. The results of these studies are summarized as follows.
- (1) As a result of the shaft alignment analysis in a straight shaft condition, it revealed that the reaction force at the forward bearing of the reduction gearbox has a negative (-) value in the static condition. This does not meet the design criteria for propulsion shaft systems, indicating that the shaft system layout may not be appropriate.
- (2) For small vessels, the low stiffness of the propeller shaft, due to its small diameter, generally the propulsion shafting system is installed in a straight shaft condition. However, in systems with reduction gearboxes, the short spacing between the gearbox bearings often leads to structural issues, such as negative (-) or extremely low positive (+) reaction forces at the forward bearing.
- (3) By adjusting the offset of the forward bearing to -0.38 mm and the aft bearing to -0.35 mm, it is confirmed that the reaction forces at the forward and aft bearings of the reduction gearbox are evenly distributed in the static condition.
- (4) In the dynamic condition, the external forces acting on the gearwheel shaft of the reduction gearbox tend to increase the bearing loads. The reaction forces at the forward and aft bearings of the reduction gearbox tends to vary inversely with the direction of the propeller bending moment. This behavior is attributed to the high RIN value resulting from the short spacing between the gearbox bearings.
- (5) For the propulsion shafting systems of small vessels with reduction gearboxes, adjusting the offsets of the forward and aft bearings in the reduction gearbox to positions below the reference line is recommended as an effective layout to maintain positive (+) reaction forces at the forward bearing. This adjustment can serve as a design guideline for propulsion shafting systems in small vessels equipped with reduction gearboxes. However, to ensure the reliability of the results of this study, future research should conduct verification through additional measurements using methods such as the jack-up method or the strain gauge measurement method
Nomenclature
| FEM : | Finite element method |
| IMO : | International maritime organization |
| MCR : | Maximum continuous rating |
| R/G : | Reduction gear |
| MOI : | Moment of inertia |
| RIN : | Reaction influence number |
| P1~P4 : | External force acting on a node |
| Up1~Up4 : | Displacement of nodes |
| ffa1 : | Section force at a1 stage |
| K : | Stiffness matrix |
| U : | Displacement row matrix |
| P : | External force row matrix |
| f : | Section force row matrix |
| F : | Force row matrix |
| R : | Bearing load after alignment |
| R' : | Initial bearing load |
| kaa1 : | Force to be applied to a1 point in order to cause a unit displacement at a1 point |
| kab1 : | Force to be applied to b1 point in order to cause a unit displacement at a1 point |
Acknowledgments
This research is the result of the national R&D project of “Development of sensors for measuring temperature, flow and pressure (RS-2024-00437086)” funded by Ministry of Trade, Industry and Energy, South Korea. All supports are gratefully acknowledged.
Author Contributions
Conceptualization, Y.G. Kim; Methodology, Y.G. Kim; Validation, Y.G. Kim; Formal Analysis, Y.G. Kim; Investigation, Y.G. Kim; Resources, Y.G. Kim; Data Curation, Y.G. Kim; Writing—Original Draft Preparation, Y.G. Kim; Writing—Review & Editing, Y.G. Kim; Visualization, Y.G. Kim; Supervision, Y.G. Kim; Project Administration, Y.G. Kim Author; Funding Acquisition, Y.G. Kim.
References
- Wartsila, E-book: 50 great wats the maritime industry could reduce its greenhouse gas emissions, Wartsila, Hilsinki, Finland pp. 1-23, 2024.
- T. K. Nam, “The latest technology of electric propulsion ship,” Journal of the Korean Society of Marine Engineers, vol. 29, no. 2, pp. 149-153 2005 (in Korean).
- J. W. Park and S. Y. Kim, “Trends in electric propulsion systems for ships,” The Journal of the Korean Institute of Power Electronics, vol. 19, no. 3, pp. 31-37, 2014 (in Korean).
- Korean Register, Control of Ship Vibration and Noise, Third edition, Textbook publisher, Republic of Korea (2012) (in Korean).
- Korean Register, Rules for the Classification of Steel Ships Part 5 Machinery Installations, Republic of Korean (2024) (in Korean).
-
R. Michel, “A quarter century of propulsion shafting design practice and operating experience in the U.S. navy,” Journal of the American Society for Naval Engineers, vol. 71, no. 1, pp. 153-164, 1959.
[https://doi.org/10.1111/j.1559-3584.1959.tb05306.x]

- H. C. Anderson, C. Henry, and J. J. Zrodovvski, “Coordinated alignment of line shaft, propulsion gear and turbine,” The Society of Naval Architects and Marine Engineers, vol. 67, pp. 449-523, 1959.
- W. E. Lehr and E. L. Parker, A method for the design of ship propulsion shaft systems, Massachusetts Institute of Technology, USA, 1961.
- W. E. Lehr and E. L. Parker, “Considerations in the design of marine propulsion shaft systems,” The Society of Naval Architects and Marine Engineers, vol. 69, pp. 555-601, 1961.
-
G. Mann, “Shipyard alignment of propulsion shafting using fair curve alignment theory,” The American Society of Naval Engineers Journal, vol. 77, no. 1, pp. 117-133, 1965.
[https://doi.org/10.1111/j.1559-3584.1965.tb05656.x]

- American Bureau of Shipping, Theoretical backgrounds shaft alignment program ShAl Ver-1.1, American Bureau of Shipping, United States of America, 2002.
- J. S. Sun, Y. G. Kim, and U. K. Kim, “A study on the shaft alignment analysis of 500ton class patron ship considering reduction gear,” Journal of Defence Quality Society, vol. 2, no. 2, pp. 95-104, 2020 (in Korean).
-
Y. G. Kim and U. K. Kim, “Design and analysis of the propulsion shafting system in a ship with single stern tube bearing,” Journal of Marine Science and Technology, vol. 25, no. 2, pp. 536-548, 2020.
[https://doi.org/10.1007/s00773-019-00659-8]

-
G. Mann, “Design of propulsion shaft systems using fair curve alignment theory,” The American Society of Naval Engineers Journal, vol. 76, no. 6, pp. 851-862, 1964.
[https://doi.org/10.1111/j.1559-3584.1964.tb04091.x]

- D. H. Moon and H. J. Jeon, “A study on the propulsion shaft alignment calculation by the matrix method of three-moment theory,” Journal of the Korean Society of Marine Engineering, vol. 5, no. 1, pp. 1-8, 1981(in Korean).
- H. J. Jeon, J. G. Park, and J. S. Choi, “Optimum alignment of marine engine shaftings by the finite element method,” Journal of the Korean Society of Marine Engineering, vol. 2, no. 1, pp. 1-14, 1978 (in Korean).
- DNV, Rules for classification of ships/high speed, light craft and naval surface craft Part 4 Chapter 4, DNV, Nor-way 2013.
- Thordon Bearing Inc., Thordon bearing sizing calculation program (No. 423885DS73), Thordon Bearing Inc., Canada 2024.
- D-I Industrial Co., Ltd., Calculation for bearing load (model : DMT460NC), D-I Industrial Co., Ltd., Republic of Ko-rea, 2024.