Winding function theory를 이용한 flux switching motor의 토크 계산
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문에서는 winding function이론을 이용하여 플럭스 스위칭 전동기의 토크 계산에 대하여 기술하였다. 먼저 플럭스 스위칭 전동기의 토크 리플을 줄이기 위하여 기존의 전동기 모델에서 회전자 형상을 최적화한 새로운 플럭스 스위칭 전동기를 제시였고, 유한요소해석을 통하여 최적화된 전동기의 토크 리플의 감소를 확인하였다. 그리고 Winding function 이론을 이용한 시뮬레이션 결과와 유한요소해석 결과를 비교 검토하였다. 또한 최적화된 플럭스 스위칭 전동기와 구동 실험 장치를 제작하였고, winding function 이론을 이용한 토크 특성 해석 결과와 실험결과를 비교한 결과로부터 winding function 이론을 이용한 해석 방법의 가능성을 확인하였다.
Abstract
This paper describes the torque calculation of Flux Switching Motor using Winding Function Theory. First of all, the optimized new Flux Switching Motor was proposed to minimize the torque ripple. The simulation results by the Winding Function Theory were compared with those from Finite Element Analysis. The revised Flux Switching Motor and experimental setup were manufactured. The simulation result by the Winding Function Theory was compared with that of the experiment. The comparison validated the analysis method of the Flux Switching Motor by Winding Function Theory.
Keywords:
Flux switching motor, Finite element analysis, Winding function theory키워드:
플럭스 스위칭 전동기, 유한요소해석, Winding function 이론1. 서 론
최근 유가와 원자재 가격의 상승이 지속이 되고, 최저 소비 효율제 시행에 따라 전동기의 고효율과 유지 보수비용의 최소화에 대한 관심이 지속적인 증가에 힘입어 유도전동기, BLDC 전동기 및 스위치드 릴럭턴스 전동기가 많이 사용되고 있다. 그러나 유도전동기는 가격은 저렴하나 운전 효율 면에서 상당히 열세이고, BLDC 전동기는 운전 효율 면에서는 유리하나 가격 측면에서 영구자석 및 구동회로의 복잡성으로 인하여 상당히 고가이므로 제품측면에서 적용하기 어려움이 있다. 스위치드 릴럭턴스 전동기는 이러한 시장의 요구에 잘 부합하는 전동기로 구조가 간단하고 가격이 저렴하며 내구성이 높아 가전제품 및 산업용 기기 등의 가변속 시스템에서 연구가 활발히 진행되고 있다. 그러나 토크의 발생원리가 회전자계에 의한 연속적인 방식이 아니라 릴럭턴스 토크를 이용하므로 토크 맥동에 의한 소음 및 진동이 발생한다는 단점이 있다[1].
플럭스 스위칭 전동기(Flux Switching Motor : FSM)는 가장 최근에 등장하고 개발된 전동기로서 스위치드 릴럭턴스 전동기나 동기형 릴럭턴스 전동기와 같이 릴럭턴스 토크를 이용하고, 고정자 및 회전자의 구조면에서는 유사하나 제어회로 및 운전 알고리즘에서는 상당히 다른 면을 보이고 있다. 특히 회로 측면에서 적은 숫자의 전력변환소자로도 토폴로지를 구성할 수 있으며 저속에서 다른 전동기에 비해 고효율의 전동기 특성을 가지고 있는 장점이 있어 선진국에서 활발히 연구 개발되고 있다. 그러나 FSM은 릴럭턴스 토크를 이용하는 전동기이므로 소음면에서는 불리한 요소가 있어 토크 리플 저감에 대한 연구가 필요하다[2].
최근 전동기 특성 해석을 위해 Winding Function 이론(Winding Function Theory : WFT)을 이용한 특성 해석 방법이 연구되고 있다. 이 방법은 공극에서의 고조파를 고려할 수 있고 해석 시간의 소요가 적은 장점을 갖고 있다. WFT를 이용한 유도전동기 특성 해석 및 고장 진단에 대한 연구도 발표되었으며[3][4], 돌극형 구조를 갖는 동기형 릴럭턴스 전동기의 특성 개선을 위한 D, Q축 인덕턴스의 차와 비를 개선하는 논문[5][6]이 발표되었다. 그러나 WFT를 FSM에 적용한 논문은 아직 없는 실정이다. 따라서 본 논문에서는 WFT를 이용한 FSM의 토크 특성 해석에 대하여 기술한다. 먼저 WFT를 적용한 특성 해석 프로그램을 완성하여 기존의 FSM의 토크 특성을 해석하고 결과를 유한요소해석(Finite Element Analysis : FEA) 결과와 비교한다. 그리고 FSM이 갖고 있는 토크 리플을 줄이기 위한 최적화된 모델을 제시하고, WFT에 의한 해석 결과와 FEA에 의한 해석 결과를 비교한다. 개선된 FSM을 제작하고 구동 장치를 구성한 후, 해석 결과와 실험결과를 비교하여 제안한 해석 방법의 가능성을 확인한다
2. Flux Switching Motor
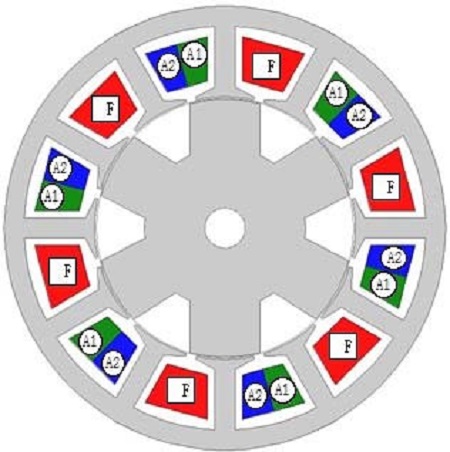
FSM은 Figure 1과 같이 필드 권선(F)과 아마츄어 권선(A1, A2)에 흐르는 전류에 의해서 발생되는 자속의 상호 작용에 의해서 만들어진 릴럭턴스 토크에 의해서 구동되고, 필드와 아마츄어 권선의 전류에 의해서 발생된 자속은 고정자와 회전자를 통하여 흐르게 된다.
필드 권선과 아마츄어 권선(A1)에 전류를 흘리게 되면 자속이 발생하게 되고, 릴럭턴스가 적은 쪽으로 정렬시키려고 하는 릴럭턴스 토크에 의해서 회전자가 정렬된다. 회전자가 고정자와 정렬하게 되면 필드 권선과 아마츄어 권선(A2)에 전류를 흘리게 되며 릴럭턴스 토크가 다시 발생하고 회전자를 정렬시키게 된다. 필드 권선과 아마츄어 권선의 자속은 회전자 폴과 고정자 극 사이의 자기저항을 최소화하기 위해 회전자와 고정자를 정렬시키고 각각의 위치에서 전류를 적절히 인가하여 릴럭턴스 토크를 발생시켜 회전자를 회전시킨다.
3. Winding Function Theory
3.1 Winding Function
WFT은 전동기에 감겨있는 권선의 형태를 고려해서 기자력의 파형을 구한 후 전동기의 토크 계산 시 필요한 인덕턴스를 계산하는 방법이다[7]. 단, 자성체의 투자율은 무한대라고 가정하고 포화는 무시한다. FSM의 상호 및 자기 인덕턴스 수식은Equation (1) 및 Equation (2)와 같다.
| (1) |
| (2) |
여기서 μ0는 공기의 투자율, r은 회전자 반지름, l 은 축방향 길이. NA(φ)는 A상 기준위치 φ에 대하여 나타내어지는 winding function , NB(φ)는 B상 기준위치 φ에 대하여 나타내어지는 winding Function, inverse air-gap function인 e-1(φ-θ)은 A상 기준위치 φ에 따른 회전자의 변화를 나타낸다. 위 수식에서도 알 수 있듯이 인덕턴스 계산에 있어서 각 상의 winding function과 inverse air-gap function의 계산이 중요함을 알 수 있다.
3.2 Inverse Air-gap Function
인덕턴스 계산에서 필요한 inverse air-gap function은 자성체 내에서 발생하는 자속의 경로에 대한 함수이며 Equation (3)로 나타낸다.
| (3) |
여기서 Es(φ)는 고정자 자속 경로, Er(φ-θ)는 회전자의 자속경로이다.
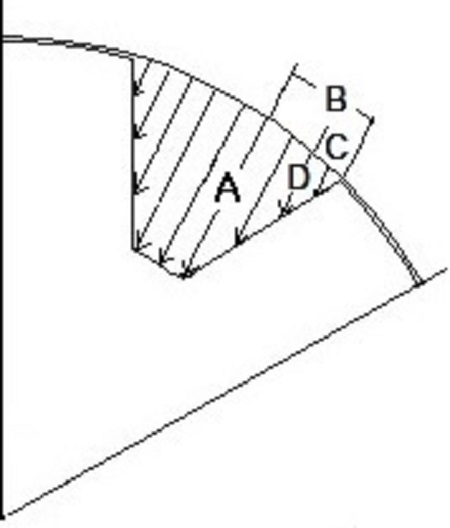
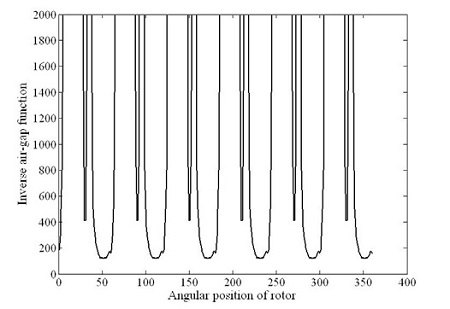
자성체의 투자율을 무한대로 보기 때문에 공기에 대한 자속의 경로만 계산하면 되므로 고정자 슬롯과 회전자의 형상에 의존하게 된다. 고정자의 형상을 이용하여 고정자 자속 경로를 계산할 수 있고[8], Figure 2의 회전자 슬롯의 자속 분포를 이용하여 자속 경로를 계산할 수 있다. 그림에서 알 수 있듯이 회전자 슬롯의 입구에서부터 자속경로는 길어지게 되며 슬롯의 최장 길이까지는 거의 선형적으로 증가됨을 예측할 수 있다. 따라서 자속경로의 길이는 Equation (4)와 같이 계산할 수 있다. Figure 3은 회전자가 고정되어 있는 경우의 inverse air-gap function의 파형을 나타낸다.
| (4) |
4. 회전자 형상 최적화
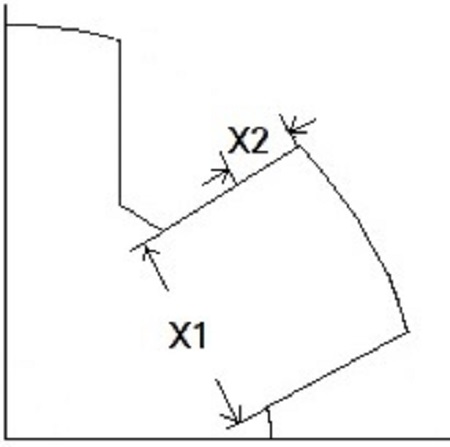
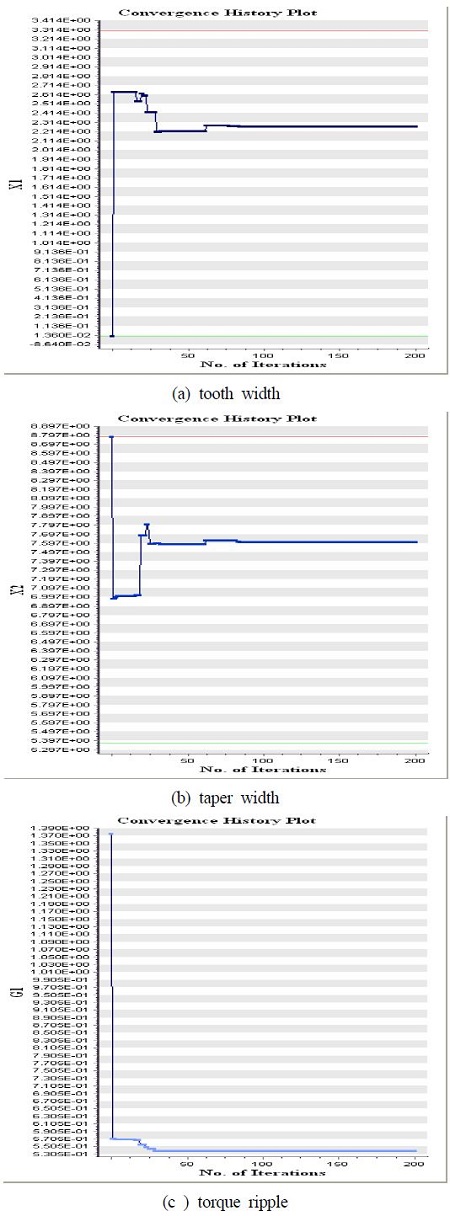
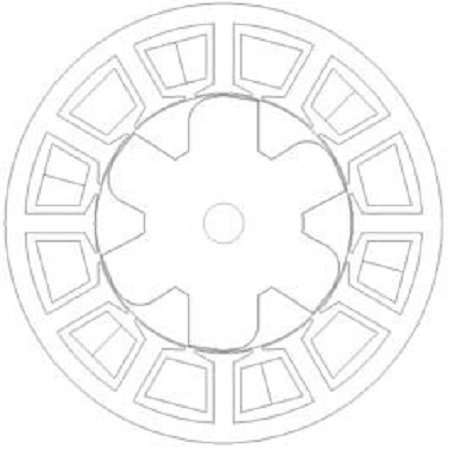
FSM의 특성상 갖고 있는 토크 리플을 줄이기 위하여 최적화 이론을 적용하여 회전자 형상을 최적화할 필요가 있다. 토크 리플에 영향을 줄 수 있는 인자들 중에서 인덕턴스의 변화를 최소화하기 위하여 Figure 4와 같이 회전자 치 폭(X1)과 회전자 치의 taper(X2)를 고려하였다. 최적화를 적용하기 위해 LHS(Latin Hypercube Sampling)을 적용하여 10개의 샘플 모델을 추출하였다. 추출한 변수들을 이용하여 각 경우별 모델에 관하여 유한요소 해석을 실행하여 목적함수인 토크 리플에 대한 결과를 도출하였다. 총 10개의 샘플 모델에 관하여 토크 리플 결과를 도출 후, 최적화 상용 프로그램인 Piano를 이용하고 일반 Kriging 기법을 적용하였다. 여기에 Direct Search 방법 중 하나인 MGA(Micro Generic Algorithm)을 적용하여 예측값을 도출하였고 최적화 결과를 Figure 5에 나타내었다. Figure 6은 최적화된 FSM의 단면도를 나타낸다.
5. 특성 해석 및 실험
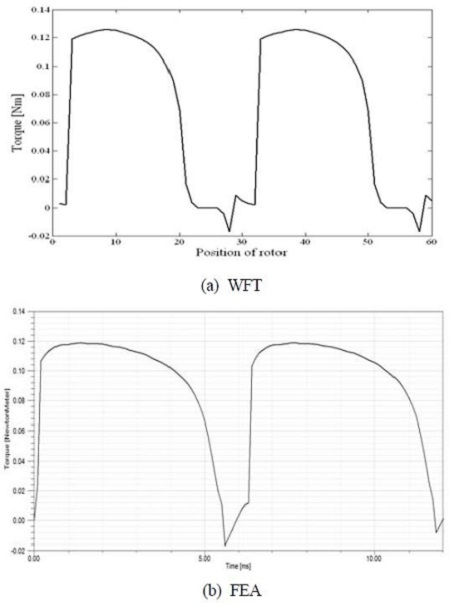
WFT를 이용하여 Matlab으로 작성한 프로그램으로 FSM의 토크 특성의 해석결과를 FEA 결과와 실험결과를 비교하였다. FSM의 턴수는 300, 입력전류는 0.64 [A], 회전속도는 800 [rpm]이다. Figure 7은 최적화 전 모델에 대한 토크 특성 해석 결과를 나타내고 Figure 8은 최적화 모델에 대한 토크 특성 해석 결과를 나타낸다. 최적화 전 모델의 토크 특성에서 역 토크가 발생하지만 최적화 모델에서는 역 토크가 발생하지 않음을 알 수 있다. WFT를 이용한 특성 해석 결과가 FEA 결과가 비슷하게 나타남을 알 수 있다. 최적화된 모델의 회전자 자속경로는 Equation (3)을 이용하였고 회전자 치의 taper에 의한 자속경로 변화를 고려하였다.
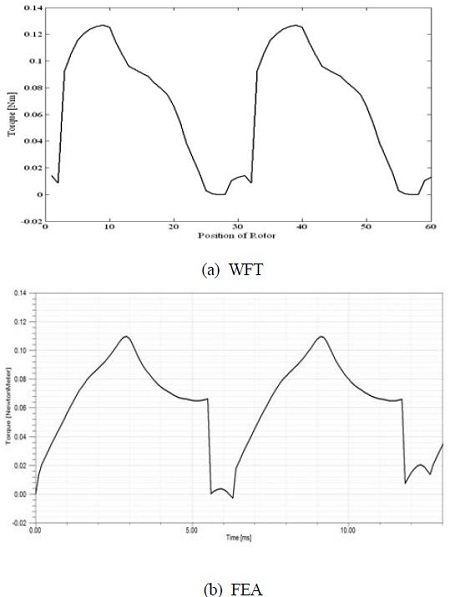
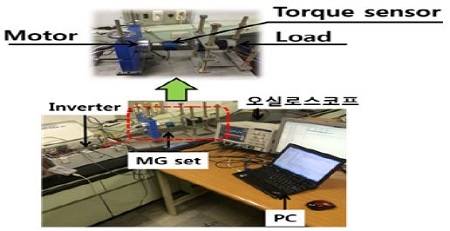
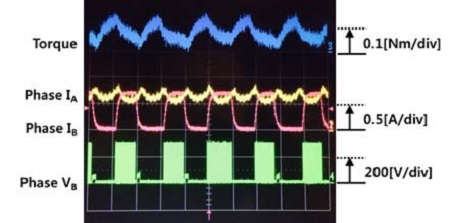
Figure 9는 FSM의 전동기의 동작 특성을 측정하기 위한 실험 장치이다. FSM 인버터를 통해 회전자를 정격속도까지 회전시킨 후 부하에 따라 전류를 증가시켰다. 정격토크까지 부하를 점차 증가시키기 위해 300W DC모터를 이용하였으며, 정상상태에서 전동기의 토크를 측정하였다. FSM의 시간에 따른 토크, 전류, 전압 특성 등은 토크센서와 오실로스코프를 통해 실시간으로 측정하였다. 토크측정용으로 사용된 토크 센서는 정격 5Nm/5V로 출력되는 Lorenz 社에 DR-2112모델을 사용하였으며 정격전압은 DC 310 [V]이며 PWM 방식으로 전류를 제어하였다. Figure 10은 최적화된 모델의 토크, 전류 및 전압 특성을 나타내며 Figure 8의 특성과 비슷하게 발생함을 알 수 있다.
6. 결 론
본 논문에서는 WFT를 이용하여 FSM의 특성해석에 대하여 설명하였다. 기존의 FSM이 갖고 있는 토크 리플의 크기를 줄이기 위하여 최적화 이론을 적용하여 회전자 형상이 최적화된 모델의 FSM을 제시하였고, 이 모델의 특성해석 결과를 FEA의 결과와 비교 검토하였다. WFT를 이용하여 Matlab을 이용한 특성해석 프로그램을 개발하였고, 기존의 FSM의 특성해석 결과를 FEA 결과와 비교하였다. 그리고 최적화된 FSM을 제작하였고, 실험 장치를 구성하여 제작된 FSM의 실험결과와 특성 해석 결과를 비교하여 제안한 해석 방법의 타당성을 확인하였다. 따라서 제안된 WFT를 이용한 특성 해석 방법은 선형적인 자계시스템 특성을 갖는 전동기의 개략적인 설계에 유용하리라 판단된다.
Acknowledgments
이 논문은 2012학년도 부경대학교의 지원을 받아 수행된 연구임(PK-2012-C-D-2012-0498).
References
- T. A. Lipo, Theory and control of synchronous machines, Lecture Notes for ECE 511, Department of Electrical and Computer Engineering, University of Wisconsin, Madison, (2002).
-
C. Pollock, and M. Wallace, “The flux switching motor, A DC motor without magnets or brushes”, IEEE Industry Application Society Annual Meeting, (1999).
[https://doi.org/10.1109/ias.1999.806009]

-
H. A. Toliyat, and T. A. Lipo, “Transient analysis of cage induction machines under stator, rotor bar and end ring faults”, IEEE Transactions on Energy Conversion, 10(2), p241-247, (1995).
[https://doi.org/10.1109/60.391888]

-
X. Luo, Y. Liao, H. A. Toliyat, A. E. Antably, and T. A. Lipo, “Multiple coupled circuit modeling of induction machines”, IEEE Transactions on Industry Applications, 31(2), p311-318, (1995).
[https://doi.org/10.1109/28.370279]

-
A. Vagati, A. Canova, M. Chiampi, M. Pastorelli, and M. Repetto, “Design refinement of synchronous reluctance motor through finite element analysis”, IEEE Transactions on Industry Application, 36(4), p1094-1102, (2000).
[https://doi.org/10.1109/28.855965]

- A. Vagati, T. A. Lipo, I. Boldea, T. Fukao, L. Malesani, and T. J. E. Miller, “Synchronous reluctance motors and drives a new alternative”, IEEE Industry Application Society, p1-1.3, (1994).
-
T. A. Lipo, Analysis of Synchronous Machines, CRC Press, p1-56, (2012).
[https://doi.org/10.1201/b12211-2]

-
T. Lubin, T. Hamiti, H. Razik, and A. Rezzoug, “Comparison between finite-element analysis and winding function theory for a inductances and torque calculation of synchronous reluctance machines”, IEEE Transactions on Magnetics, 43(8), p3206-3410, (2007).
[https://doi.org/10.1109/TMAG.2007.900404]