γ-type Stirling Engine의 Yoke crank 설계 단순화에 관한 연구

2.1 γ-type 스털링엔진

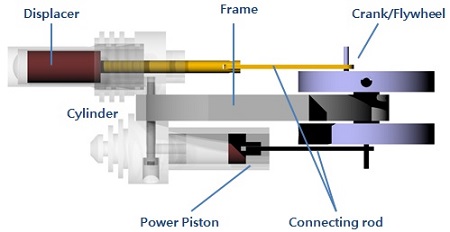
γ-type 스털링엔진은 Figure 2에서 보여주는 것과 같이 크게 파워 피스톤, 디스플레이서 피스톤, 각각의 실린더, 크랭크 및 플라이휠로 구성되어 진다.

Figure 2:

Structure of the γ-type stirling engine

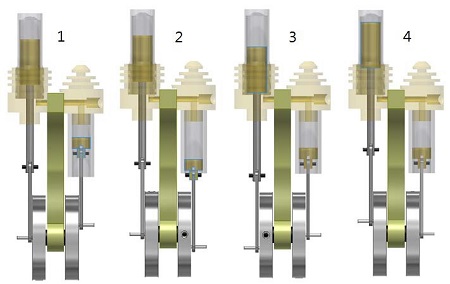
일반적으로 γ-type의 경우 β-type과 동일한 열 교환 메커니즘에 의해서 작동하나 디스플레이서 실린더와 파워 피스톤 실린더가 분리된 두 개의 실린더 구조로 1개 이상의 냉각관로를 통하여 연결되어지는 형태로 구성된다. 스털링엔진은 4개의 동작행정으로 작동하게 되는데, ① 파워 피스톤이 봉입가스를 압축함과 동시에 디스플레이서 피스톤이 봉입가스를 고온부로 밀어 올려 열 교환하는 과정, ② 가열된 봉입가스의 상승된 압력에 의하여 파워 피스톤을 밀어내는 Power stroke(팽창 행정) 과정, ③ 디스플레이서에 의해서 냉각실린더로 잔여봉입가스를 밀어내는 과정, ④ 플라이휠의 회전력으로 다시 냉각된 봉입가스를 압축하는 과정으로 이루어진다.

Figure 3과 같이 사이클이 유지되기 위해서는 파워 피스톤과 디스플레이서 피스톤의 위상이 90°로 위치해야 하며 그 경우에 가장 큰 출력을 얻을 수 있다.

Figure 3:

Simple cycle schematic diagram of the γ-type stirling engine

2.2 위상차와 크랭크 구조

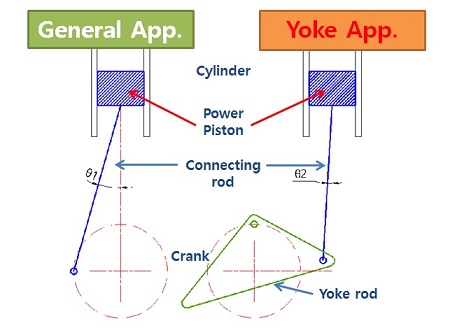
앞서 기술한 바와 같이 스털링엔진의 봉입기체의 압축과 팽창을 파워 피스톤과 디스플레이서 피스톤을 통하여 4개의 행정과정을 1 Cycle로 하여 열에너지를 기계에너지로 전환한다. 이를 유지하기 위해서는 파워 피스톤과 디스플레이서 피스톤의 상하운동의 위상차를 90°가 되도록 유지해 주어야 한다. β-type을 제외하고 보통은 크랭크 각을 90°로 유지하여 설계를 하나 이는 실험 등을 위하여 가장 단순하게 구성할 수 있다. 다만 실린더와 크랭크 축, 플라이휠의 배치에 있어 자유도가 크게 떨어지는 특성이 있어 필요에 의해 다중실린더 형태로 구성될 경우 용적이 커지는 경향이 있다. 대표적인 형태가 α-type의 직교형 실린더 구조로 회전축을 중심으로 하여 1개의 크랭크 암에 두 커넥팅로드(connecting rods)가 체결되는 형태로 구성된다. 또한 γ-type의 경우 크랭크축과 플라이휠을 일체화 하거나 분리하는 형태 등으로 다양한 형태가 있다.

2.3 Ross Yoke 설계

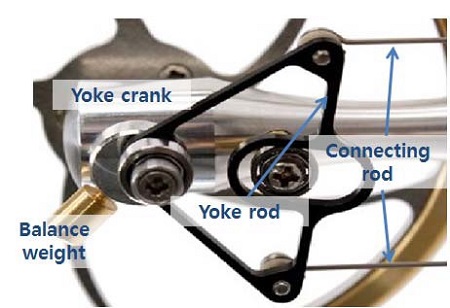
Ross Yoke는 스털링엔진과 같은 두 개의 연동된 피스톤의 상하운동을 회전운동으로 전환하도록 고안된 특징적 구조로 크랭크축을 기준으로 두 개의 실린더가 90°위치가 아닌 0°에 위치한다. Figure 4에서 보여주는 것과 같이 일반적인 크랭크 구조와 비교하여 커넥팅로드와 피스톤 각 변위가 상대적으로 매우 작은 장점으로는 피스톤의 상하 운동에 따른 피스톤과 실린더 벽에 가해지는 횡력이 적고, 무엇보다 시스템의 용적을 줄일 수 있는 특징이 있다. Figure 5는 일반적인 α-type 스털링 엔진의 Yoke driver의 이미지 이다.

Figure 4:

General application of the α-type ross yoke driver

Figure 5:

Schematic of Ross Yoke driver

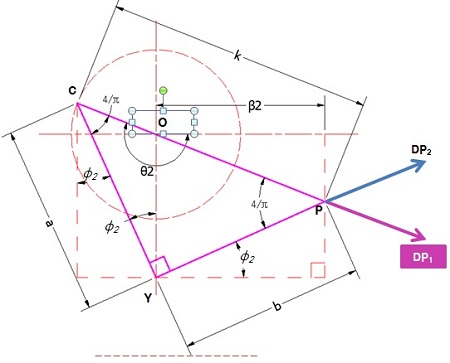
또한 종래의 Yoke 다양한 설계방법을 Figure 5와 Equation (1)을 통하여 설명하고 있으며, 해당 식을 이용할 경우 기본설계 시 특정하여야 하는 조건 변수의 량이 많은 특징이 있고, 무수히 많은 경우의 설계 값을 산출할 수 있다. 피스톤의 동일 스트로크에 대하여 다양한 값이 나올 수 있음으로 설계 진입에 있어 각 정수를 특정하기가 어려운 문제가 있다[6].

2.4 γ형 Ross Yoke driver의 파워 피스톤 측 Yoke crank의 설계

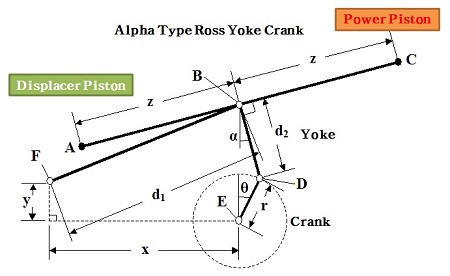
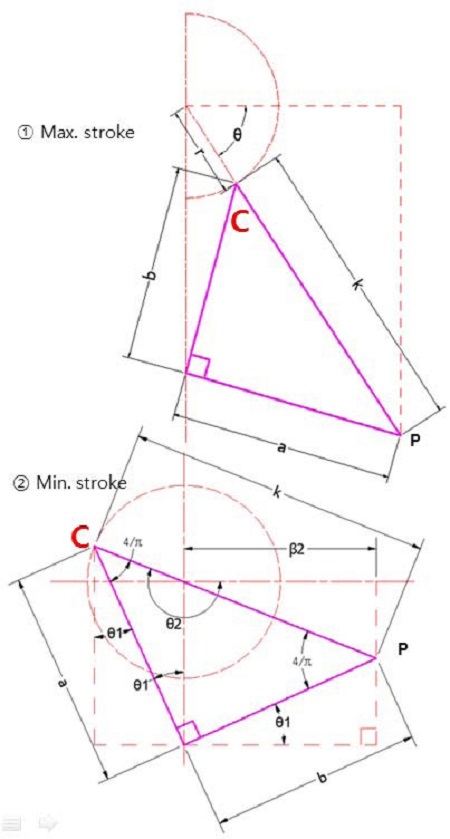
앞서 논의한 바와 같이 Ross Yoke driver는 종래 α-type 스털링엔진에 주로 적용되었다. 금번 연구에서는 driver를γ-type 엔진에 설계 적용하여 Figure 6에서 보여주는 것과 같이 크랭크와 피스톤 구간의 물리적 크기와 실린더와 피스톤에 가해지는 횡력을 종래보다 줄이며 시스템의 병렬화에 유리하게 하는 목적이 있다. 다만, α-type 엔진에서와는 달리 디스플레이서 피스톤의 stroke가 파워 피스톤의 stroke 보다 길어야 하는 특징으로 인하여 크랭크축과 연결되는지 rod의 형태가 Figure 4와 5에서 보는 바와 같이 종래의 등변삼각형이 아닌 모델로 설계가 됨으로 파워 피스톤 측과 디스플레이서 피스톤 측의 rod를 개별 설계하여야 한다. Figure 7는 파워 피스톤 측의 최대-최소 stroke 상태에서 각각의 크랭크 위치와 크랭크 반경 및 Yoke rod의 위치를 도식화하여 보여주고 있다. 즉 크랭크축을 기준으로 최대, 최소 stroke는 다음과 같이 정리가 가능하다.

Figure 6:

Difference of crank arm angles between the respective applications

Figure 7:

Schematic diagram of Max. and Min. strokes at ross yoke driver

즉, Figure 7의 ①과 같이 크랭크축을 중심으로 점 C(crank-yoke 접속점), P(Connecting rod 접속 점)가 일직선이 될 때 최대 stroke, ②와 같이 $$ \overrightarrow{\mathit{CP}}$$가 크랭크축의 중심을 지날 때 최소 stroke를 구성하게 된다.

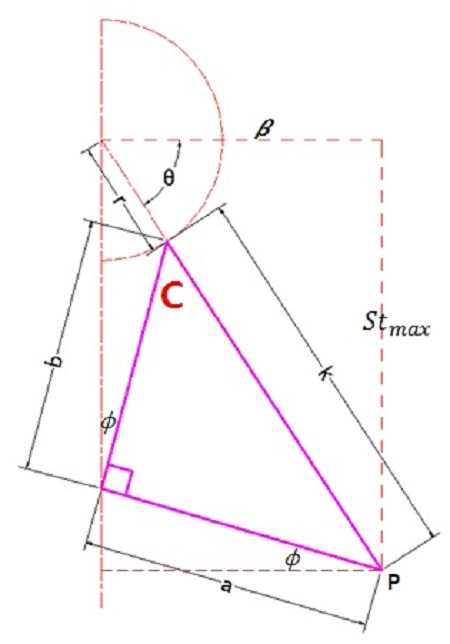
Figure 8에서 최대스트로크 상태에서의 St_max와 β, 회전각 θ에 대한 관계를 확인해야 한다.

수식으로 정리하면 다음과 같다.

Figure 8:

Relation between the Crank and Yoke angular maximum Stroke status

여기서, β는 커넥팅 포인트와 축간 거리, Φ는 요크 중심각 θ는 크랭크각, a는 b는 크랭크 축과 요크중심간 거리, r은 크랭크반지 이다. a, b의 길이는 실제 크기와 비율에 의해서 피스톤의 stroke에 영향을 미친다. 소형엔진에서는 등변으로 값을 설정할 경우 엔진의 회전에 따른 진동이 커지는 경향이 있으나, 중대형 엔진에 있어서는 a, b를 같은 값으로 설정하여도 무방하다. 따라서 a = b로 설정하면 다음과 같이 정리된다.

asinΦ = β

식 (1), (2)를 통하여 다음과 같이 정리할 수 있다.

또한, a = b 일 경우 $$ \mathit{\Phi }={\mathit{\theta }}_1-\frac{\mathit{\pi }}{4}$$ 임으로 식 (5)에 대입하여 정리하면 다음과 같다.

cosθ₁, sinθ₁에 대하여 정리하면 다음과 같다.

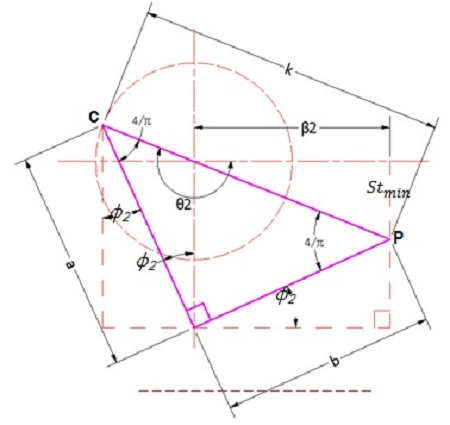
또한, Figure 9에서 최소 stroke 상태를 도식화 하여 최대 stroke에서와 같은 방법으로 정리하면 다음과 같다.

Figure 9:

Relation between the Crank and Yoke angular minimum Stroke status

또한, 최소 stroke는 Figure 9에 도식된 크랭크와 Yoke의 위치, 크랭크 각에 의해서 다음과 같이 계산할 수 있다.

실재 Yoke driver와 링크된 Piston의 stroke(L_st)는 상기의 식 (7)과 (9)에 의해서 다음과 같이 정리될 수 있다.

2.5 상-하사점에 따른 Yoke rod와 커넥션로드의 위상차

Figure 10에 도식한 바와 같이 Ross Yoke driver의 하사점에 따른 θ₁의 각도에 의하여 피스톤과 Yoke rod를 연결하는 connecting rod의 횡 측 위상(lateral phase)이 동 위상에 위치하지 않고 틀어지는 결과를 야기한다. 시뮬레이션과 계산에 의하여 살펴보면 θ₁이 55°를 기준으로 하여 그보다 작은 값이면, Figure 7의 P와 같이 상사점일 때의 커넥팅 포인트와 거의 동 위상에 위치하게 되나, 그 보다 큰 값에서는 급격하게 Figure 10의 P₂와 같이 우측으로 평행 이동한 위상으로 벌어지는 결과 일부 피스톤과 실린더 간 횡력이 증대되는 결과를 야기한다.

Figure 10:

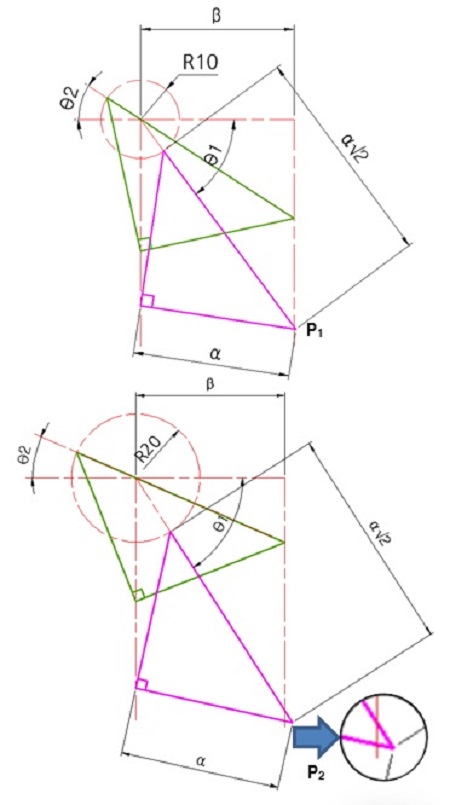
Comparison of the lateral phase between the top and bottom dead point of piston in accordance with θ1

이를 피하기 위해서는 다음 같은 방법에 의해서 설계하여야 한다.

즉 Equation (6)에 의하여 r, a의 값이 결정되면 θ₁의 값이 결정되는 방법에 의한다. 다만, Equation (11)과 같이 θ₁은 55° 보다 작은 값으로 설정한다.

2.6 γ-type Ross Yoke driver의 디스플레이서 피스톤 측 Yoke crank의 설계

앞서 논의 한 바와 같이 일반적으로 Ross Yoke driver는 α-type Stirling engine의 크랭크에 적용할 경우 크랭크와 각각의 Yoke rod가 등변삼각형의 형태를 취한다.

하지만, γ-type의 엔진에서는 디스플레이서 피스톤과 파워 피스톤의 변위가 대략 2:1 내외의 비대칭 형태의 stroke길이를 가짐으로 인하여 Yoke rod의 형태가 등변 삼각형의 형태가 될 수 없다. 또한, 디스플레이서 피스톤과 파워 피스톤의 위상차가 90°를 유지하기 위해서는 Figure 11에서 보는 것과 같이 Yoke rod의 connection poin P가 DP₁ 방향으로 신장되어야만 한다. 만약 DP₂ 방향으로 신장될 경우 상하사점의 중심축과의 위상이 등변위일 때의 위상에서 벗어나는 결과로 stroke의 길이가 늘어나는 특징은 동일하게 가지나 위상차는 90°를 넘어서게 되는 결과를 갖게 되고 커넥션로드와의 접속점의 횡축 위상은 거의 직선상에 위치하여 DP₁ 방향으로의 신장에 비하여 디스플레이서 rod에 걸리는 횡력은 적어진다.

Figure 11:

Relation between the Elongation direction and connection points of displacer piston

이에 반하여 DP₂ 방향으로의 신장의 경우는 Figure 11 와 12에서 보여주는 것과 같이 connection point의 궤적이 크게 변형됨으로 인하여 디스플레이서 피스톤과 연결되는 connection rod에 걸리는 횡력이 증가하게 되어 이를 보완하기 위해서 Figure 13의 설명과 같이 connection rod의 길이를 디스플레이서 피스톤의 상하 운동에 저항하지 않는 범위 내에서 최대한 길게 하여야 횡력이 적어지는 특징을 갖는다.

Figure 12:

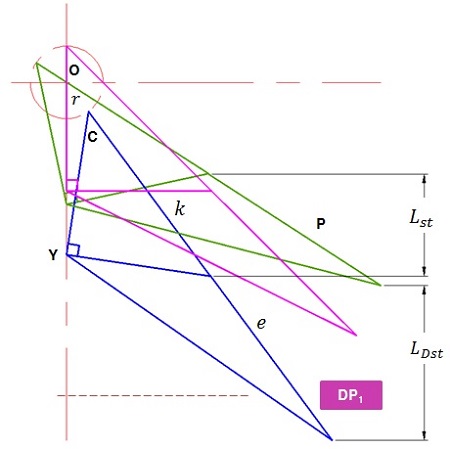
To correct phases between power piston and displacer piston, the connection point is elongated to the DP1 direction. According to these, lateral forces on the displacer rod and connection rod increase.

Figure 13:

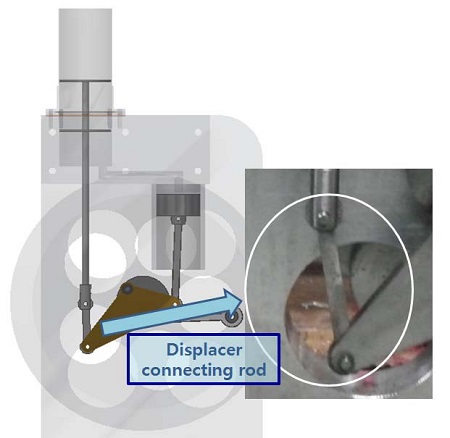
Lateral force to the connection rod according to the elongated yoke rod for displacer piston connection point and variation of connection rod length to reduce the lateral force

앞선 논의에서 파워 피스톤의 상하운동에 따른 stroke 길이는 이미 Equation (10)을 통하여 확인하였다.디스플레이서 피스톤의 stroke 길이 L_Dst는 다음 식 (12)와 같이 정리하여 설계에 반영한다.

디스플레이서 피스톤과 파워 피스톤의 스트로크 거리 비율 R_st는 식 (12)을 통하여 식 13)과 같이 정리할 수 있으며, R_st는 파워 피스톤의 스트로크 거리와 실린더의 최대 부피를 통하여 가열하고자 하는 봉입기체의 총량을 구하고, 이를 통하여 디스플레이서 실린더 내의 공기량과 디스플레이서의 체적을 구하면 디스플레이서 피스톤의 상하 스트로크 거리를 알 수 있으며, 이미 파워 피스톤의 stroke 거리를 계산과정에서 상수로 구하는 단계를 거치게 됨으로 R_st는 비율로서 상수화 할 수 있다. 아울러 θ₁, θ₂, L_st, 모두가 상수로 둘 수 있음으로 e 값만 구하면 디스플레이서 피스톤의 link point의 Yoke 설계를 마무리 할 수 있다.