부분구조 모드합성법에 의한 주파수응답함수 산출법
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
진동해석에 있어서 매우 중요한 부분 중의 하나가 주파수응답함수를 구하는 것이다. 크거나 복잡한 구조물은 일반적으로 아주 큰 자유도-예를 들면 수 백 만 자유도-를 가지기 때문에 역행렬에 의한 전통적인 방법으로는 주파수응답함수를 구할 수 없을지도 모른다. 그래서 전체 구조물을 몇 개의 부분구조로 나누어서 해석하는 부분구조 해석법을 이용한다. 여기에서는 부분구조별로 나누어 계산한 부분구조 진동모드를 이용하여 자유도를 현격하게 낮춘 등가의 저 자유도 모델에서 주파수응답함수를 구하는 방법을 제시한다. 개발한 프로그램의 신뢰도를 확인하기 위하여 평판 구조물에 적용하여서 실험과 축소하지 않는 영역에서의 해석 결과와 본 해석 결과를 비교하였고, 매우 좋은 결과를 얻었다.
Abstract
A very important part in vibration analysis is to calculate the frequency response function (FRF). In general, a large sized or/and complicated structure has many thousands to millions of degrees. Therefore, the FRF cannot be calculated by the traditional analysis method using an inverse matrix. This paper presents a new FRF calculation method of a superstructure by synthesizing sub-structure modes, of which the DOF can be deduced by partitioning into some sub-structures. To confirm its analysis results, the method was applied to an assembled plate (B300 x L900 x t5 mm) with three diagonal sub-plates(B300 x L300 x t5 mm) in series and compared with the measured data. The test results have were comparable those of the calculated ones with an error less than 5%.
Keywords:
FEM, Vibration analysis, Sub-structure, Sub-structure mode synthesis method, Frequency response function키워드:
유한요소법, 진동해석, 부분구조, 부분구조 모드합성법, 주파수응답함수1. 서 론
유한요소법은 구조해석과 진동해석을 하는데 필수적인 수단이 된지 이미 오래다. ANSYS나 MSC/ NASTRAN, ABAQUS, ADAMS, ADINA, LS-Dyna, FLUENT 등 수많은 상용의 도구를 이용하면 설계 단계에서부터 모든 사항을 고려할 수 있기 때문에 최적설계가 가능해지고, 이미 제작이 완료된 구조물에 대하여서도 안전성 진단 및 설계변경 도구로 이용할 수 있다. 그럼에도 불구하고 이러한 상용 프로그램들은 구입하거나 사용하는데 비용이 많이 들고 지원프로그램들이 많기 때문에 사용하는 방법이 매우 까다롭다. 그래서 연구자들은 누구나 손쉽게 사용할 수 있도록 matlab을 이용한 진동해석 프로그램을 개발하여 발표한 바 있다[1].
연구자들이 개발한 프로그램은 자유도가 큰 구조물의 진동해석을 위하여 부분구조합성법[2]을 사용하였다. 부분구조합성법이란 전체 구조물을 작은 부분구조로 나누고, 부분구조 사이의 결합조건을 적용시켜서 전체 구조물을 해석하는 기법을 말한다.
구조물의 정적인 해석은 일차방정식을 푸는 알고리즘이 발달함에 따라서 부분구조합성법이 그리 큰 매력을 주지 못한다. 그러나 부분구조진동해석에서는 단순한 행렬의 조작이 아닌 부분구조물을 극도로 축소된 자유도의 등가 모델로 바꾸어서 결합하여 해석하기 때문에 그 효율성이 매우 뛰어난다.
주파수응답함수를 구하기 위하여서는 아주 큰 행렬의 역행렬을 구하여야 하는데, 여기에서는 부분구조의 진동모드와 결합부의 연결 조건을 이용하여 자유도를 현저하게 축소시켜서 주파수응답함수를 구하는 방법에 대한 프로그램을 개발하고, 그 유효성을 보이기 위하여 실제 구조물에 적용시켜 주파수응답함수를 구하고, 실험을 통하여 그 결과를 확인한다.
2. 모드합성법에 의한 주파수응답함수
2.1 운동방정식과 주파수응답함수
설명을 위하여 구조물의 운동방정식을 다음과 같이 둔다.
| (1) |
여기에서 M은 질량행렬, K는 강성행렬, f는 외력이고, x는 응답이다. 주파수응답함수를 구하기 위하여 외력을 조화함수로 두기로 하면, 응답도 조화함수로 표시된다.
| (2) |
| (3) |
식 (2)와 (3)을 (1)에 대입하여 정리하면 다음과 같이 된다.
| (4) |
| (5) |
따라서 응답은 쉽게 다음과 같이 구해진다.
| (6) |
| (7) |
여기에서 G는 전달함수나 주파수응답함수로 불리는 외력에 대한 응답의 주파수영역에서의 비례함수이며, 외력에 따른 변위의 비례함수를 컴플리언스(compliance)라고 한다.
식 (7)에서 알 수 있듯이 주파수응답함수를 구하기 위하여서는 구조물의 자유도에 해당하는 역행렬을 구해야 하는데 자유도가 커지면 통상의 방법으로는 역행렬을 구하기도 힘들고, 시간도 대단히 많이 걸리게 된다.
참고로 matlab에서의 메모리의 사용을 보기 위하여 다음과 같은 간단한 프로그램을 실행하여 보면 메모리 사용량이 증가함에 따라 계산시간이 어느 정도 소요되는지를 알 수 있다.
| Program 1: Memory test program of Matlab |
사용한 컴퓨터는 Windows 7 64 비트 환경으로 메인보드는 GIGABYTE의 GA-X58A-UD3R로 Intel Core i7 프로세서를 사용하고, 메인 메모리는 8GB, 보조기억장치는 삼성 840 Pro SSD를 사용하고, 가상 메모리는 8GB로 설정하였다. 이 단순한 프로그램을 실행하여 걸린 시간이 무려 40.6초에 달하였고, n을 50,000으로 하면 ‘저장용량 초과(out of memory)’라는 경고메시지와 함께 계산이 중단되었다. 보다 실질적으로 주파수응답함수를 구하기 위한 구체적인 예에 적용시키기 위하여 다음과 같은 프로그램을 실행하여 보았다.
| Program 2: Cpu time check for the calculation of FRF by Matlab |
절점을 1,000, 2,000, 3,000, 4,000, 5,000개로 하고, 자유도는 1점 6자유도로 하여 질량행렬과 강성행렬을 rand 함수로 만들고 주파수를 5Hz부터 5Hz 간격으로 1,000Hz까지 계산하는 과정이다. 그러나 절점이 1,000개인 경우에 대하여서도 주파수응답함수 G를 모두 저장하면 용량초과로 계산이 불가능하기 때문에 단지 1개의 주파수에 대하여서만 주파수응답을 구하였다. 프로그램에는 생략하였지만, 이 방법으로 주파수응답함수를 구하려면 주파수마다의 주파수응답함수를 200번 구하여 보조기억장치에 저장하기를 반복하여야 하기 때문에 단순히 200배의 계산 시간보다 훨씬 더 걸릴 것임을 예상할 수 있다.
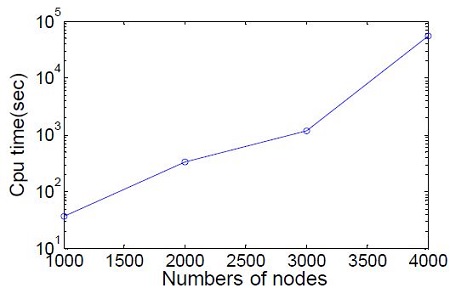
Table 1 및 Figure 1에 절점증가에 따른 계산시간(cpu time)의 증가를 보인다.
종축의 계산시간은 절점증가에 따라 지수적으로 증가하고 있다.
2.2 부분구조 모드합성법에 의한 진동해석
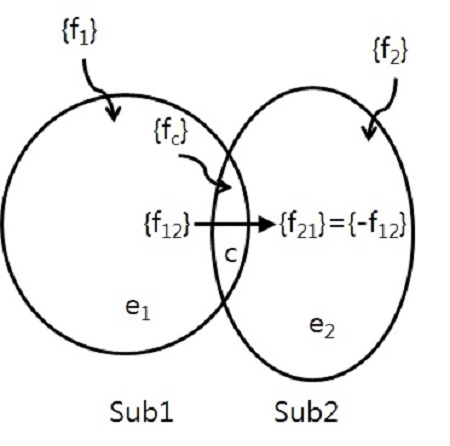
설명을 간단히 하기 위하여 구조물을 Figure 2와 같이 제일 단순한 2개의 부분구조로 나누어 감쇠가 없는 경우로 가정하면 다음과 같은 수학적 모델로 표현될 수 있다.
여기에서 e는 결합부를 제외한 본체 영역이고, c는 다른 부분구조와 결합부 영역을 나타내며, 숫자 1, 2는 부분구조 번호를 나타내고, x는 변위, f는 외력, f12는 부분구조 사이에 주고받는 상호 작용력을 나타낸다.
| (8) |
| (8)’ |
2.3 Guyan의 정축소와 부분구조 모드를 이용한 자유도 축소
식 (8)은 모델만 부분구조별로 한 것이기 때문에 이대로 해석한다면 오히려 해석의 자유도가 결합부의 자유도만큼 증가하여 해석상 이득이 전혀 없다.
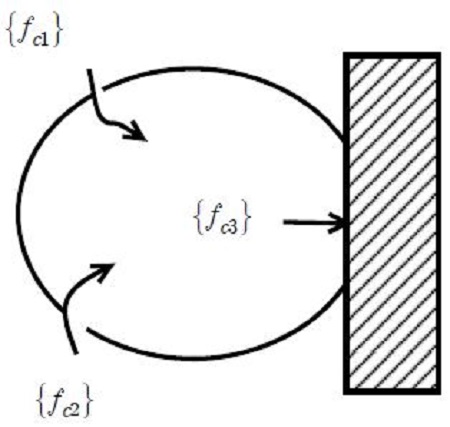
그래서 Guyan의 정축소법[3]이 등장하게 되는데, Guyan의 정축소의 원리는 다음과 같다. Figure 3에서 외력이 작용하지 않은 부분 (e)와 외력이 작용하는 부분 (c)로 나누어서 외력과 강성 및 변위의 관계를 나타내면 다음과 같이 된다.
| (9) |
| (10) |
따라서 외력이 작용하지 않은 부분의 변위는 다음과 같이 외력이 작용하는 부분의 변위로 표시될 수 있다.
| (11) |
단,
| (12) |
여기에서 이 T를 Guyan의 정 축소행렬(static reduction matrix)이라 한다. 식 (11)을 식 (9)에 대입하면 다음과 같이 방정식이 결합부의 자유도만으로 축소되어 표시된다.
| (13) |
따라서 외력이 작용하지 않은 부분이라도 외력이 작용하는 부분으로 표시되어 자유도를 외력이 작용하는 부분의 자유도만으로 표시할 수 있다. Guyan의 정축소법을 이용하면 자유도가 결합부의 자유도로 축소되어 자유도가 대폭적으로 줄어들게 된다. 이 방법은 정적인 문제의 해법에는 수학적으로 완벽하기 때문에 오차가 생기지 않으나, 진동해석과 같은 동적인 문제해결에 적용하면 질량의 항을 무시하였기 때문에 고주파 영역일수록 오차가 커진다. 이를 보완하기 위하여 Hurty[4]와 Benfield [5]가 부분구조별로 해석한 부분구조모드(sub-structure mode)를 이용하였고, 이를 통하여 오차를 훨씬 줄였다.
Hurty의 방법은 Guyan의 정축소(static reduction)에 더하여 다음과 같이 부분구조의 저차 모드를 채용하여 자유도를 축소하는 방법이다.
| (14) |
| (15) |
삭 (14)를 식 (8)에 대입하고 앞에 Tm’을 곱하면 다음과 같이 축소된 자유도의 운동방정식을 얻게 된다.
| (16) |
여기에서 T1과 T2는 Guyan의 정축소 행렬이고, ϕe는 결합부를 완전히 고정한 상태로 가정한 부분구조의 고유진동모드 행렬이다. 또 ϕe와 ξ는 부분구조 해석에서 채용한 모드의 수와 같은 자유도를 가진다. 즉 2개의 부분구조에서 채용한 부분모드의 수와 결합부의 자유도의 합으로 전체 구조물의 자유도가 축소되는 것이다. 상기 식 (16)을 계산하면 축소된 영역에서의 고유진동수와 고유진동모드를 구할 수 있다. 이것을 식 (14)에 대입하면 원래 물리적 좌표계에서의 고유진동 모드를 구할 수 있다.
2.4 부분구조 모드합성법에 의한 주파수응답 함수
식 (16)은 축소된 영역에서의 운동방정식이다. 따라서 이 영역에서의 주파수응답함수는 식 (7)을 구할 때 적용된 과정을 따르면 다음과 같이 구해진다.
| (17) |
| (18) |
또 식 (14)로부터 원래 좌표계로 환원하면 원래의 물리적 좌표계에서의 주파수응답함수는 다음과 같이 구해진다.
| (19) |
즉 물리적 좌표계에서 주파수응답함수는 식 (7)에서 알 수 있는 바와 같이 전 자유도에 대한 행렬의 역행렬을 구해야하지만, 부분구조 모드합성법을 이용하면 식 (18)에서와 같이 부분구조해석에서 채용한 저차의 십 수개 내지 수십 개의 자유도와 결합부의 자유도를 합한 것이 축소된 영역에서의 자유도가 되기 때문에 좌표변환 행렬과 축소된 자유도의 역행렬의 계산의 곱으로 주파수응답함수를 구할 수 있다.
3. 프로그램의 작성
3.1 부분구조 모드합성 주파수응답함수 계산 프로그램
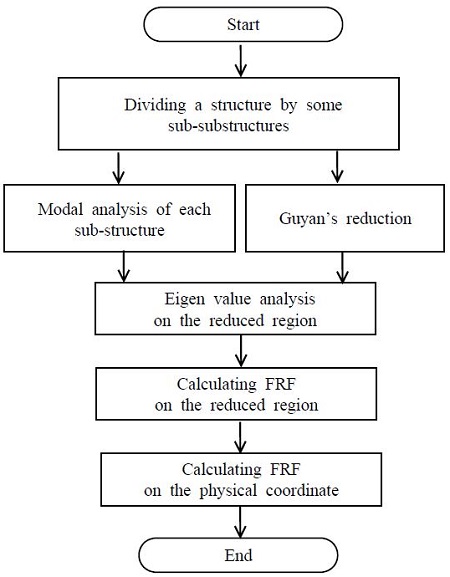
부분구조 모드합성법을 이용한 부분주파수응답함수를 구하는 프로그램의 흐름은 Figure 4에 보이는 바와 같다. 먼저 전체 구조물을 분할하기 용이한 몇 개의 부분구조로 나눈 다음, 각 부분구조를 적당한 유한요소로 분할한다. 각각의 부분구조는 비결합부와 결합부로 나눈다. 각 부분구조물에 대하여 비결합부만의 고유치 문제를 풀어서 비결합부를 저차의 20개 정도의 진동모드로 자유도를 축소하고, 결합부와 합하여 고유치를 구한다. 만약에 구조물 사이가 스프링으로 연결되어 있으면 강결합으로 처리하지 않고 스프링을 부가하여 해석한다.
프로그램의 구성은 크게 각 부분구조의 설계 자료를 이용하여 결합 정보를 알아내는 선행 프로그램과 이를 이용하여 부분구조의 고유진동수와 고유진동모드를 구하는 과정, 정축소행렬을 구하는 과정, 이를 이용하여 식 (15)의 축소행렬 Tm을 만드는 과정을 거쳐서 식 (16)의 축소된 영역에서의 운동방정식에서 고유치를 해석을 하는 부분으로 이루어진다.
4. 적용 예
4.1 해석 모델
폭 300mm, 길이 900mm, 두께 5mm인 평판을 3등분 하여 300 × 300(mm2)인 정사각형 평판 셋으로 나누어서 개발한 프로그램으로 해석한다. 평판의 밀도는 7860kg/m3, 종탄성계수는 205GPa, Poisson 비는 0.3이고, 전혀 구속되지 않은 상태로 해석하고, 자유지지를 실현하기 위하여 철판에 작은 구멍을 두 곳에 뚫어서 공중에 매달아 철판에 수직인 방향은 거의 구속되지 않게 하여 실험한다.
Figure 5는 하나의 부분구조를 보인다. 50 × 50 (mm2)의 정사각형 요소로 분할하였고, 절점 번호는 그림과 같이 1~49로 부여하였다. 이와 똑같은 부분구조가 셋으로 된 되어있는 예에 대하여 적용한다.
Table 2는 전체 구조물을 하나의 모델로 계산했을 경우의 자유도와 셋으로 나누어 계산했을 경우의 자유도에 대하여 나타낸다. 자유도가 약 1/6로 줄었음을 알 수 있다.
이 효과는 복잡한 구조물에 적용하면 훨씬 더 극적으로 나타난다. 예를 들어 100,000 절점으로 분할된 구조물의 진동해석은 Table 1에서 알 수 있듯이 위에서 사용한 계산기로는 해석이 불가능하다. 그러나 이를 50개의 부분구조로 쪼개어 대략 한 구조물 당 약 2500 절점 정도로 나눌 수 있다면 어렵지 않게 계산할 수 있다는 것을 알 수 있다.
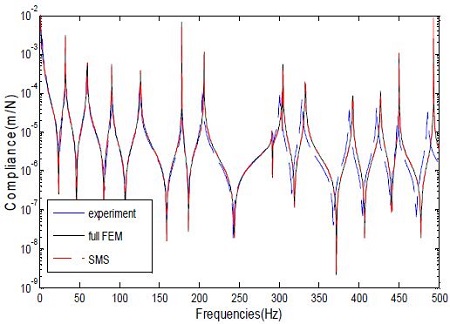
Figure 6은 모델에 대한 주파수응답함수를 보인다. 구조물의 맨 귀퉁이를 가진하고, 가진점의 응답에 대한 그림이다. 쇄선이 실험한 결과이고, 실선이 하나의 구조로 해석한 식 (7)에 의한 계산 결과이고, 일점쇄선이 제안한 방법 식 (19)에 의한 부분구조 모드합성법을 이용한 결과이다. 실험 결과와 비교하면 200Hz 근방인 6차 고유진동수까지는 거의 완벽하게 일치하고 있음을 알 수 있고, 고차로 가도 상당히 잘 일치하고 있다.
또 제안한 SMS에 의한 주파수응답함수가 하나의 구조물로 해석했을 때의 full FEM 모델의 결과와 거의 완벽하게 일치함을 알 수 있다.
Table 3은 각 차수별 고유진동수를 나타낸다. 오차는 축소하기 전 모델에 대한 고유진동수에 대한 축소 후의 모델 해석에 대한 것으로 거의 완벽하게 일치함을 알 수 있다. 실험은 단지 유한요소법 자체의 유효성을 나타내는 참고용으로 본 연구의 핵심과는 거리가 있으므로 언급하지 않는다.
5. 결 론
본 연구에서는 부분구조 모드합성법을 이용하여 주파수응답함수를 구하는 방법을 제안하였으며 다음과 같은 결론을 얻었다.
- 1. 부분구조 모드합성법을 이용하여 통상의 개인용 PC로 100,000 절점을 가진 모델에 대하여 주파수응답함수를 별 무리 없이 구할 수 있음을 알 수 있었다.
- 2. 실제 구조물에 적용하여 실험 결과와 비교하여 거의 완벽한 주파수응답함수를 얻을 수 있음을 보였다.
- 3. 전체구조물을 하나로 모델로 한 주파수응답함수와는 거의 전 영역에서 주파수응답함수가 일치함을 보였다.
References
-
S. C. Park, J. R. Kim, and K. I. Park, “Sub-structure mode synthesis vibration analysis program development using Matlab”, Journal of the Korean Society of Marine Engineering, 38(6), p666-673, (2014).
[https://doi.org/10.5916/jkosme.2014.38.6.666]

- A. Nagamatsu, M. Okuma, Component Mode Synthesis Method, Japan, Baifukan, (1991).
-
R. J. Guyan, “Reduction of stiffness and mass matrices”, AIAA Journal, 3(2), p380, (1965).
[https://doi.org/10.2514/3.2874]

-
W. C. Hurty, “Dynamic analysis of structural systems using component modes”, AIAA Journal, 3(4), p678-685, (1965).
[https://doi.org/10.2514/3.2947]

-
W. A. Benfield, and R. F. Hruda, “Vibration analysis of structures by component mode substitution”, AIAA Journal, 9(7), p1255-1261, (1971).
[https://doi.org/10.2514/3.49936]