유한 대용량 안테나 시스템에서 송수신기 설계 방법

1. 서론

초기 다중 안테나 통신 시스템에 대한 연구는 일대일 무선 통신 환경에 초점을 맞춰 이루어졌다. 최근에는 다중 사용자간 다이버시티(diversity) 이득을 얻을 수 있도록 다중 안테나를 장착한 기지국이 공간 다중화(spatial multiplexing) 방식으로 여러 사용자와 통신하는 시스템, 즉 다중 사용자 다중 안테나 시스템으로 연구 방향이 진화하였다. 최근 RF 소자 기술의 발전과 더불어 기지국에 대용량 안테나를 장착하는 다중 안테나 기술에 대한 논의가 주목 받고 있다. 그 대표적인 방법으로 정합 필터(matched-filter) 선형 송신기를 이용해 다중 사용자간 간섭을 줄이는 대용량 안테나 기술 즉 massive MIMO(multiple-input multiple output) 기술이 있다[1]. 또한 참고 문헌[2][3]은 대용량 안테나 시스템에서 단순한 정합 필터 송신기를 적용하더라도 송신 안테나 수가 무한히 커질 경우 다중 사용자 간섭을 완전히 억제할 수 있음을 이론적으로 밝혔다. 그러나 기지국 안테나 수가 유한하게 커질 경우 1) 다중 사용자간 간섭이 여전히 존재해 정합 필터 송신기로는 다중 안테나 하향링크 방송 채널 (MIMO downlink broadcast channel)의 전송 용량(capacity)를 달성할 수 없다.

한 편, 다중 안테나 하향링크 방송 채널의 전송 용량을 achieve 방법으로 DPC(Costa's dirty paper coding)[4]이 알려져 있다. 그러나 하드웨어 구현이 불가능할 정도의 큰 복잡도로 인해 DPC 방법을 실제 시스템에 적용하기는 어렵다. 그래서 ZF(zero-forcing) 빔포밍 방법[5], BD(block-diagonal-ization) 방법[6], 일반화된 채널 인버젼(G-CI) 방법[7] 등 다양한 선형 송신 기법이 연구되었다. 이러한 방법들은 다중 사용자 간섭을 효과적으로 억제할 수 있으나, 전송 용량 관점에서 최적화되지 않았다. 다중 안테나 하향링크 방송 채널에서 전송용량을 극대화하는 선형 송수신기 설계 방법으로 가중치 평균 자승 오류율(weighted mean squared error; WMSE) 최소화를 통해 송수신기를 구하는 방법이 알려져 있다[8]. 그러나 Christensen et al. [8] 방법도 DPC 방법과 마찬가지로 송신 안테나 개수가 증가할수록 연산 복잡도가 커져, 대용량 안테나 시스템에 적용하기 어렵다.

본 논문에서는 유한 대용량 안테나를 장착한 기지국이 다수의 셀 경계 영역(cell-edge) 사용자를 지원하는 경우, 전송 용량을 최대화하는 선형 송수신기 설계 방법을 다룬다. 즉 기지국은 낮은 신호 대 잡음 비(signal-to-noise-ratio; SNR) 환경의 다수 사용자들과 유한 대용량 안테나를 사용해 동시에 통신한다. 이러한 환경에서 전송 용량을 최대화하는 두 단계 선형 프리코더(precoder) 설계 방법을 제안한다. 우선 첫째 단계 프리코더로 정합 필터를 적용한다. 이를 통해 낮은 신호 대 잡음 비에서 통신하는 셀 경계 영역 사용자에게 빔포밍 이득(beamforming gain)을 제공할 뿐만 아니라, 채널 행렬과 정합 필터의 곱으로 이뤄진 유효 채널 (effective channel)의 dimension을 줄일 수 있다. 둘째 단계 프리코더는 첫째 단계에서 만들어진 유효 채널을 토대로 전송 용량을 최대화하는 해를 구한다. 시뮬레이션 결과와 분석을 통해, 유한 대용량 안테나 기지국이 다수의 셀 경계 영역을 동시에 지원하는 경우 제안하는 방법이 효과적으로 전송 용량을 최대화함을 확인했다. 제안하는 방법은 가중치 평균 오류율을 최소화하는 방법으로 전송율을 극대화하는 선형 송수신기를 구한다는 점에서 Christensen et al. [8] 과 유사하다. 그러나 Christensen et al. [8]은 다중 사용자 다중 안테나 하향 링크 채널을 그대로 사용하는데 비해, 제안하는 방법은 빔포밍 이득(beamforming gain)과 채널 di-mension 축소 효과를 위해 정합 필터를 곱한 유효 채널을 기반으로 한다. 그 결과 제안하는 방법은 송수신기 구현 복잡도를 크게 증가시키지 않으면서 셀 경계 영역 사용자의 전송 용량을 극대화할 수 있다.

2. 시스템 모델

3. 제안하는 두 단계 선형 송수신기 설계

다중 안테나 다중 사용자 환경에서 전송 용량을 극대화하기 위해서, Christensen et al. [8]은 가중치 평균 자승 오류율 최소화 기법을 기반으로 가중치 전송률 합을 최대화하는 선형 송수신기 설계 방법을 제안하였다. 그러나 Christensen et al. [8]의 방법은 연산 복잡도가 송신 안테나 개수의 세제곱에 비례하는 단점이 있어, 대용량 안테나 시스템에 적용하기 어렵다. 본 논문에서는 유한 대용량 안테나 시스템에서 Christensen et al. [8] 방법의 연산량 복잡도 문제와 다중 사용자 간섭으로 인한 정합 필터 방법의 성능 저하 문제를 해결하기 위해 두 단계 선형 송수신기 설계 방법을 제안한다.

여기서는 일반성을 잃지 않으면서 송신기 구조를 T_k = A_kB_k와 같이 가정한다.

3.2 둘째 단계 선형 송신기 설계

앞서 설명한 대로 유한 대용량 안테나 시스템에서는 정합 필터를 적용하더라도 다중 사용자간 간섭이 제거되지 않는다. 이제 이러한 residual 다중 사용자간 간섭을 고려해 전송 용량을 최대화하는 둘째 단계 선형 송신기를 구한다. 이를 위해 수신기는 다음과 같이 평균 자승 오류율 최소화(minimizing mean squared error; MMSE) 수신기로 가정한다.

$\[ D_k=\frac{1}{\sqrt{g_k}}{B}_k^H{H}_k{H}_k^H{\left(H_k{H}_k^H{B}_k{B}_k^H{H}_k{H}_k^H+H_k\sum _{i\cancel{=}k}^K{H}_i^H{B}_i{B}_i^H{H}_i{H}_k^H+\frac{{\sigma }_n^2}{g_k}{I}_{N_r}\right)}^{-1} \]$

(7)

Equation (7)의 MMSE 수신기를 적용할 경우, k번째 사용자에 대한 오류 행렬(error matrix)은 다음과 같다.

$\[ \begin{array}{c}{\Psi }_k=E\left\{\left(D_k{y}_k-\widehat{s_k}\right){\left(D_k{y}_k-\stackrel{{}^{}}{s_k}\right)}^H\right\}\\ ={\left(I_{N_r}+g_k{\Phi }_k^{-1}{H}_k{H}_k^H{B}_k{B}_k^H{H}_{k}H\right)}^{-1}\end{array} \]$

(8)

여기서 $$ {\mathit{\Phi }}_{\mathit{k}}={\mathit{g}}_{\mathit{k}}{\mathit{H}}_{\mathit{k}}\sum _{\mathit{i}\cancel{=}\mathit{k}}^{\mathit{K}}{\mathit{H}}_{\mathit{i}}^{\mathit{H}}{\mathit{B}}_{\mathit{i}}{\mathit{B}}_{\mathit{i}}^{\mathit{H}}{\mathit{H}}_{\mathit{i}}{\mathit{H}}_{\mathit{k}}^{\mathit{H}}+{\mathit{\sigma }}_{\mathit{n}}^2{\mathit{I}}_{{\mathit{N}}_{\mathit{r}}}$$이다. Equation (8)의 오류 행렬을 이용해 전송 용량을 다음과 같이 나타낼 수 있다.

$\[ {\mathit{R}}_{\mathit{tot}}=\sum _{\mathit{k}=1}^{\mathit{K}}\log (\det ({\mathit{\Psi }}_{\mathit{k}}^{-1}\mathrm{))} \]$

(9)

Equation (9)로 표현되는 전송 용량을 최대로 하는 송신기는 다음의 가중치 평균 자승 오류율 최소화 문제를 이용해 구할 수 있다.

$\[ \begin{array}{c}\min \sum _{\mathit{k}=1}^{\mathit{K}}\mathit{Tr}({\mathit{W}}_{\mathit{k}}{\mathit{\Psi }}_{\mathit{k}})\hfill \\ \mathit{s}.\mathit{t}.\mathit{Tr}({\mathit{H}}_{\mathit{k}}^{\mathit{H}}{\mathit{B}}_{\mathit{k}}{\mathit{B}}_{\mathit{k}}^{\mathit{H}}\mathit{H})={\mathit{P}}_{\mathit{t}}\hfill \end{array} \]$

(10)

여기서 $$ {\mathit{W}}_{\mathit{k}}\in {\mathit{C}}^{{\mathit{N}}_{\mathit{r}}\times {\mathit{N}}_{\mathit{r}}}$$ 은 평균 자승 오류율(mean squared er-ror; MSE)의 가중치를 의미한다. Christensen et al. [8] 에 따르면,

$\[ {\mathit{W}}_{\mathit{k}}={\mathit{\Psi }}_{\mathit{k}}^{-1} \]$

(11)

평균 자승 오류율의 가중치를 Equation (11)과 같이 정하면 전송 용량 최대화 문제의 해와 가중치 평균 자승 오류율 최소화 문제의 해가 같아진다. 즉 두 문제의 최적 송신기가 같아진다. 따라서 전송 용량을 최대화하는 둘째 단계 선형 송신기는 다음 식을 이용해 구할 수 있다.

$\[ \begin{array}{c}\sum _{k=1}^{K}E\left\{Tr\left(W_k{s}_k-{\beta }^{-1}\widehat{s_k}\right){\left(s_k-{\beta }^{-1}\widehat{s_k}\right)}^H\right\}\\ s.t.\sum _{k=1}^{K}Tr\left(H_k^H{B}_k{B}_k^H{H}_k\right)=P\end{array} \]$

(12)

여기서 {W_k}은 Equation (11)을 이용해 구하고 β 는 전송 전력을 조절하는 파라미터이다.

행렬에 대한 미분 공식을 이용해, Equation (12)를 만족하는 둘째 단계 선형 송신기는 다음과 같다.

$\[ {\mathit{B}}_{\mathit{k}}=\mathit{\beta }{{\mathit{B}}_{\mathit{k}}}^{\prime } \]$

(13)

여기서

$\[ {B_k}^{\text{'}}={\left(\sqrt{g_k}{H}_k{H}_k^H{D}_k^H{W}_k{D}_k{H}_k{H}_k^H+\frac{{\sigma }_n^2}{g_k{P}_t}Tr\left(W_k{D}_k{D}_k^H\right)H_k{H}_k^H\right)}^{-1}{H}_k{H}_k^H{D}_k^H{W}_k \]$

그리고

$\[ \mathit{\beta }=\sqrt{\frac{{\mathit{P}}_{\mathit{t}}}{\sum _{\mathit{k}=1}^{\mathit{K}}\mathit{Tr}({\mathit{H}}_{\mathit{k}}^{\mathit{H}}{{\mathit{B}}_{\mathit{k}}}^{\prime }{{\mathit{B}}_{\mathit{k}}^{\mathit{H}}}^{\prime }{\mathit{H}}_{\mathit{k}})}} \]$

로 쓸 수 있다.

지금까지 MMSE 수신기와 MSE 가중치 그리고 둘째 단계 송신기를 차례로 구했다. 이들 세 파라미터는 각각 다른 파라미터들이 주어져있다는 가정 하에서 해당 파라미터를 유도했다. 따라서 각 파라미터 간 상호 의존 관계를 고려해 Algorithm 1과 같이 교차 반복 연산 알고리즘으로 둘째 단계 최적 송신기를 구할 수 있다.

각각의 파라미터를 고정한 연산은 볼록 문제의 해를 구하는 과정이므로 Algorithm 1은 local 최적 해로 수렴한다.

Algorithm 1  최적 둘째 단계 송신기 및 수신기 구하는 방법

4. 성능 분석 및 시뮬레이션 결과

4.1 연산 복잡도 분석

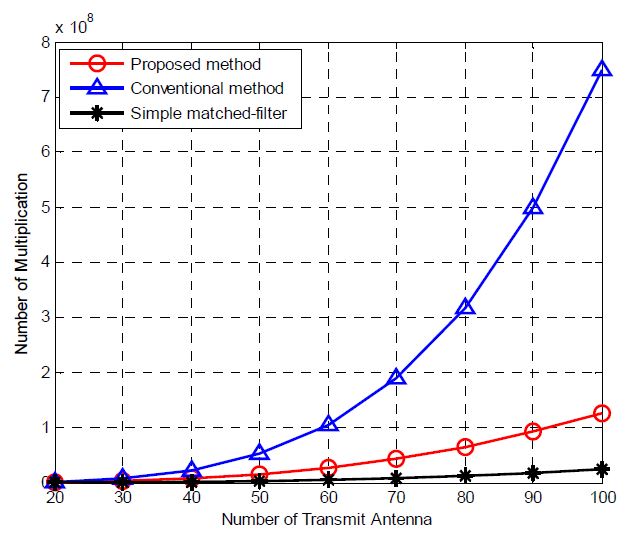
본 절에서는 제안하는 방법의 연산 복잡도를 분석하고 Christensen et al. [8]과 2.2절의 정합 필터 방법의 연산 복잡도와 비교한다. 하드웨어 구현시 복잡도가 가장 큰 연산인 복소수 곱 연산의 횟수를 연산 복잡도의 기준으로 정한다. Figure 1은 송신 안테나 개수에 따른 연산 복잡도의 비교 결과이다. Christensen et al. [8]은 송신기를 구하는 과정에서 주된 연산이 송신 안테나 개수, 즉 사용자 수와 수신 안테나 수의 곱의 세제곱 (KN_r)³에 비례한다. 반면 제안하는 방법은 주된 연산이 수신 안테나 수의 세제곱 N_r³에 비례한다. 그 결과 제안하는 방법이 Christensen et al. [8]에 비해 연산 복잡도 관점에서 상당히 효율적임을 확인할 수 있다. 하지만 2.2절의 정합 필터 방법은 반복 연산 없이 해를 구하는데 반해, 반복 연산이 필요한 제안하는 방법은 정합 필터 방법에 비해 연산량이 많다. 그러나 아래의 시뮬레이션 결과에서 확인할 수 있듯이 제안하는 방법이 정합 필터 방법에 비해 전송 용량 관점에서 낫다.

Figure 1:

The computational complexity

4.2 시뮬레이션 결과

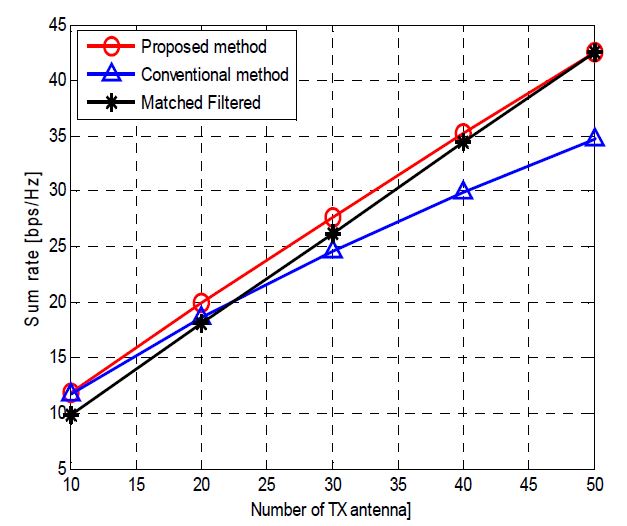
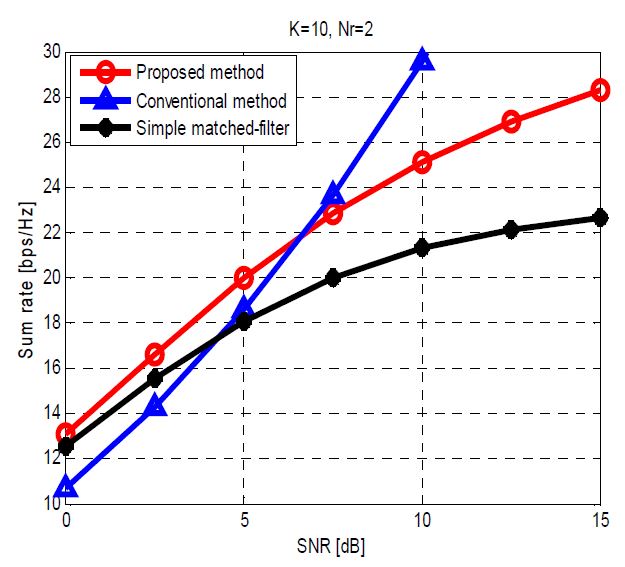
본 절에서는 시뮬레이션을 통해 제안하는 방법의 평균 전송 용량 성능을 확인한다. 시뮬레이션에서 신호 대 잡음 비는 SNR = $$ \frac{{\mathit{P}}_{\mathit{t}}}{{\mathit{\sigma }}_{\mathit{n}}^2}$$으로 정의한다. Figure 2는 N_r = 2, 셀 경계에 해당하는 낮은 신호 대 잡음 비; 즉 SNR = 5 [dB] 에서 제안하는 방법(circle-mark), Christensen et al. [8] 방법(triangle-mark), 그리고 2.2절의 정합 필터 방법의 평균 전송 용량 성능을 보여준다. 유한 대용량 안테나 환경에서 제안하는 방법의 우수함을 확인하기 위해, 다양한 개수의 송신 안테나에 대해 시뮬레이션을 실시하였다. Lemma 2에서 예상할 수 있듯이, 송신 안테나 개수가 증가함에 따라 제안하는 방법과 정합 필터 방법의 전송 용량 성능이 수렴한다. 그러나 송신 안테나 개수가 50 개 이하인 유한 대용량 안테나 환경에서는 제안하는 방법의 전송 용량 성능이 우수함을 확인할 수 있다. 이는 제안하는 방법이 residual 다중 사용자 간섭을 고려해 전송 용량을 최대화하는 송수신기를 구하기 때문이다. Figure 3은 K = 10, N_t = 20, 그리고 N_r = 2 일 때 다양한 신호 대 잡음 비에서 전송 용량 성능을 보여준다. 낮은 신호 대 잡음 비 영역에서 성능을 보면, 제안하는 방법과 정합 필터 방법이 Christensen et al. [8] 의 기존 방법보다 전송 용량이 큼을 확인할 수 있다. 이는 첫째 단계 프리코더인 정합 필터의 빔포밍 이득에 의해 유효 수신 신호 대 잡음 비(effective SNR)가 향상되었고, 그 효과가 잡음이 주된 환경(noise dominant); 즉 낮은 신호 대 잡음비 영역에서 분명히 나타나기 때문이다. Figure 3을 통해 유한 대용량 안테나 기지국이 셀 경계 영역 다중 사용자를 지원하는 경우, 제안하는 방법이 가장 좋은 성능을 보임을 알 수 있다.

Figure 2:

The sum-rate performance over various number of transmit antennas when SNR = 5 [dB]

Figure 3:

sum-rate performance over various SNRs

Acknowledgments

이 논문은 2014학년도 한국해양대학교 신진교수정착연구비 지원을 받아 수행된 연구임.

References

• F. Rusek, D. Persson, B. K. Lau, E. G. Larsson, T. L. Marzetta, O. Edfors, and F. Tufvesson, “Scaling up MIMO: Opportunities and challenges with very large arrays”, IEEE Signal Processing Magazine, 30, p40-60, (2013). [https://doi.org/10.1109/MSP.2011.2178495]
• T. L. Marzetta, “Noncooperative cellular wireless with unlimited numbers of base station antennas”, IEEE Transactions Wireless Communications, 9, p3590-3600, (2010). [https://doi.org/10.1109/TWC.2010.092810.091092]
• E. G. Larsson, O. Edfors, F. Tufvesson, and T. L. Marzetta, “Massive MIMO for next generation wireless systems”, IEEE Communications Magazine, 52, p186-195, (2014). [https://doi.org/10.1109/MCOM.2014.6736761]
• M. H. M. Costa, “Writing on dirty paper”, IEEE Transactions Information Theory, 29, p439-441, (1983). [https://doi.org/10.1109/TIT.1983.1056659]
• C. B. Peel, B. M. Hochwald, and A. L. Swindlehurst, “A vector perturbation technique for near-capacity mult-iantenna multi-user communication - Part I: Channel inversion and regularization”, IEEE Transactions Communications, 53, p195-202, (2005). [https://doi.org/10.1109/TCOMM.2004.840638]
• Q. H. Spencer, and A. L. Swindlehurst, M. Haardt, “Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels”, IEEE Transactions Signal Processing, 52, p461-471, (2004). [https://doi.org/10.1109/TSP.2003.821107]
• H. Sung, S. R. Lee, and I. Lee, “Generalized channel inversion methods for multiuser MIMO systems”, IEEE Transactions Communications, 57, p3489-3499, (2009). [https://doi.org/10.1109/TCOMM.2009.11.070404]
• S. S. Christensen, R. Agarwal, E. Carvalho, and J. M. Cioffi, “Weighted sum-rate maximization using weighted MMSE for MIMO BC beamforming design”, IEEE Transactions Wireless Communications, 7, p4792-4799, (2008). [https://doi.org/10.1109/T-WC.2008.070851]
• 3GPP TR 36.211 V 12.3.0 (Release 12), “Evolved Universal Terrestrial Radio Access (E-UTRA)”, (2014).