Direct orientation estimation through inertial odometry based on a deep transformer model
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Studies on the inertial measurement unit (IMU), a fundamental localization solution for mobile devices in inertial odometry have been conducted. Most inertial odometry approaches focus on the two-dimensional space; however, technological advancements demand the accurate measurement of movements in the three-dimensional (3D) space, making 3D inertial odometry algorithms essential. Three-dimensional inertial odometry calculates the relative pose based on IMU-measured data, and the estimated pose denotes the displacement encountered by the sensor within a unit of time. Subsequently, the trajectory is generated through integration. However, many existing approaches are characterized by drift errors owing to the integration processes utilized to estimate position and orientation. We propose an extended direct orientation inertial odometry network (DO IONet) that directly estimates the orientation to overcome drift errors, improving the estimation performance of the 3D translation vector. The proposed approach calculates the orientation by inputting linear acceleration, gyroscope, gravity acceleration, and geomagnetic values, overcoming drift errors associated with orientation estimation. The extended DO IONet comprises an encoder for local feature extraction and a decoder for sequential feature extraction. The proposed model doesn't require structural initialization and doesn't cause drift error because an integration process is not required to estimate the orientation.
Keywords:
Inertial odometry, Six degrees of freedom, Drift, Neural network, Transformer1. Introduction
Odometry is a positioning technique that estimates relative positions from an initial set of coordinates using sensors within a platform [1]-[3]. Therefore, odometry is primarily utilized in systems that require independent motion tracking, such as drones, vehicles, and vessels, as well as in systems that demand precise motion recognition, such as healthcare, sports monitoring, and gaming. Odometry methods are classified into four categories based on the sensor type: visual odometry (VO) utilizing a camera, light detection and ranging (LiDAR) odometry (LO), radar odometry (RO), and inertial odometry (IO) utilizing an inertial measurement unit (IMU) [4].
VO estimates the trajectory of a platform by analyzing the differences between adjacent frames and the current frame collected by a camera, which can be a monocular camera [5][6] or stereo [7][8]. VO technology utilizes a high-performance localization method; however, the multiple images utilized as input data occupy significant storage space, and the computational algorithms are correspondingly complex, requiring high-performance hardware.
Generally, LO calculates the current position by matching a two-dimensional (2D) terrain map generated using the laser speckle pattern created at each time step. Recently, active studies into approaches to generate precise 3D terrain maps by utilizing improved laser system designs that enable 3D scanning with LiDAR have been conducted [9]-[11]. Similar to LO, RO aligns scans acquired via radar sensors that utilize radio waves for determining the positions of surrounding objects, thereby estimating the relative position of the platform [12]-[14]. This approach is being applied in commercial autonomous driving technology due to its robust operation, even in adverse weather conditions. However, both RO and LO utilize time-series data in the form of 3D arrays as input and involve computationally intensive algorithms, including exponential functions, that must be executed repeatedly. Therefore, applying them to mobile devices with limited storage and computational capacity is challenging.
IO can generate the trajectory of a platform by utilizing an IMU sensor that outputs acceleration, gyroscope, and geomagnetic data [15][16]. Input data for IO encompasses all the features related to 3D motion and has an extremely small data size. Additionally, this approach can estimate the orientation in the reference coordinate system as it utilizes acceleration and magnetometer data as input. Therefore, IO is essential to operate a positioning system in a constrained environment where initial values other than position coordinates are not defined. IO can be utilized as a solution for location correction in environments, such as underground spaces and mountains that render the application of infrastructure-based positioning technologies challenging.
In particular, IO is most suitable for measuring movements at a submeter scale. However, this approach has two inherent problems. First, the ambiguity in setting the initial pose of the platform. Ideally, the trajectory can be accurately estimated by utilizing an initial pose value obtained from sensor data collected in a known environment. However, setting the initial pose can be challenging in common scenarios with devices, such as smartphones and smartwatches that generally utilize inertial sensors. While velocity initialization can be achieved through platform control steps, initializing orientation values is considerably difficult, as it cannot be constrained by the user's azimuth. The second problem is drift error, which results from the continuous integration of the pose over time when generating trajectories. During this process, the noise inherent in the pose data over the unit time interval is also integrated, resulting in considerable errors in the pose when generating trajectories over extended periods. This problem can be mitigated by periodically resetting the pose values.
Conventional IO approaches include strapdown inertial navigation systems (SINS), which continuously integrate pose over a unit time interval to output the current position, and pedestrian dead reckoning (PDR), which enhances the trajectory estimation performance by initializing poses at specific points. SINS is the most intuitive method to estimate relative pose changes by integrating acceleration and angular velocity output from IMUs [17]-[20]. However, it inevitably introduces drift error because it involves multiple integration steps during trajectory generation. Consequently, most SINS techniques aim to improve trajectory generation performance by analyzing the noise originating from IMU sensors in a multidimensional manner [21][22]. PDR utilizes the fact that the walking speed becomes zero while walking, and except for azimuth, orientation remains relatively constant, to output 2D position changes [23][24]. The PDR approach leverages the knowledge of when the foot makes contact with the ground to address the ambiguity problems in setting the initial pose of the platform and drift error. However, owing to the integration of step length and azimuth value in trajectory generation through PDR, drift error occurs, and it remains a 2D odometry approach [25].
Recently, a novel approach called inertial odometry network (IONet) has been proposed as an IO technique. IONet utilizes a low-cost IMU and is based on deep neural networks. Most IONets input sequential inertial data into recurrent neural networks to output pose over unit time intervals [26][27]. Subsequently, the integrated values of these changes are utilized to generate a trajectory. IONet can effectively reduce drift errors by utilizing all sequential data. The resulting trajectory is similar to that obtained by utilizing the conventional IO method. IONet exhibits superior trajectory generation performance compared with SINS, which compensates for measurements based on assumptions regarding the error model. However, as the estimation time increases, the increasing drift error results in greater pose ambiguity. These factors can influence the trajectory estimation accuracy.
This study proposes an extended direct orientation inertial odometry network (DO IONet) that improves the ambiguity in setting the initial pose of the platform and drift error by directly estimating the orientation, thereby eliminating one integration step. The proposed approach circumvents the two problems by leveraging the DO IONet framework to accept inertial data as input and generate the velocity and orientation as outputs. To augment the DO IONet's performance, we conducted experiments by utilizing various network architectures. Consequently, we observed that the extended DO IONet, composed of an encoder with convolutional layers to extract local features and a decoder with transformer blocks to extract sequential features, outperformed alternative methods. This method considerably improved the orientation and 3D translation errors, outperforming the existing DO IONet by over 10%.
The primary contributions and innovations of this study can be succinctly outlined as follows:
- 1. The proposed DO IONet framework directly estimates orientation from low-cost IMU data, eliminating drift errors.
- 2. The proposed extended DO IONet method improves the estimation performance of orientation and 3D translation vectors.
- 3. The proposed method is suitable for various applications, as it enables the estimation of orientation within the reference coordinate system without orientation initialization.
2. Related Studies
2.1 Three-DOF Inertial Odometry Network
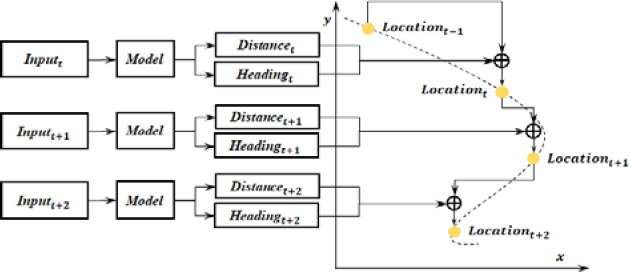
The degree of freedom (DOF) refers to the number of axes utilized to represent pose changes. In the context of IO, 3-DOF IO estimates the relative position changes in a 2D plane, as shown in Figure 1. During unit time intervals, the collected IMU data are fed to a 3-DOF IO model, which outputs the distance and heading. These resultant values can be represented as 2D vectors and are referred to as relative position changes, which are added to the previous location, indicating the current position. [26] represented the pioneering learning-based IO approach. The method utilizes a support vector machine to classify motions captured by IMUs, including standing, walking, and turning, and subsequently regress pose vectors. The pose vectors are integrated to generate trajectories in a 2D plane. IO-Net introduced the Oxford inertial odometry dataset (OxIOD), which comprises various types of inertial data. It estimates trajectories in a 2D plane by feeding 2-second-long accelerations and angular velocities into two layers of long short-term memory (LSTM) networks [27][28]. This was the first approach to apply deep neural networks to inertial data and generate trajectories by utilizing raw data. Furthermore, [29] proposed an approach to alleviate the computational burden of recurrent neural networks by introducing a lightweight variant of LSTM, called WaveNet. [30] introduced a loss function for orientation, orientation change, and velocity in the reference coordinate system to enhance velocity estimation performance. However, these methods are limited in that, similar to PDR, they can only generate trajectories in a 2D plane.
2.2 Six-DOF Inertial Odometry Network
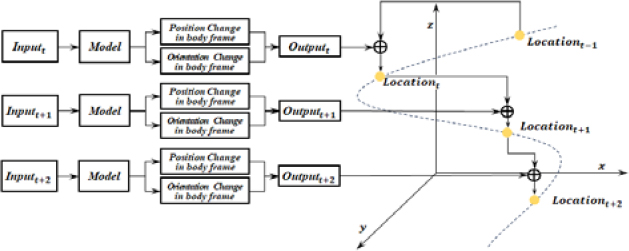
Six-DOF IO represents the change from the initial pose of the platform in 3D space, as shown in Figure 2. The pose includes the position, which can be expressed by utilizing the x-axis, y-axis, and z-axis coordinates, and orientation, represented by the roll, pitch, and yaw angles. The position and orientation changes in the body frame represent the changes in pose over a unit of time. These pose changes in the body frame can be transformed into a 3D translation vector in the reference coordinate system by considering the previous pose. The current pose can be expressed as the sum of a 3D translation vector from the starting point. Compared with 3-DOF IO, 6-DOF IO utilizes three additional coordinate representations, resulting in a considerable increase in drift error owing to the additional orientation computations required. The initial 6-DOF IONet employed a neural network composed of convolutional layers and LSTM to estimate 3D pose changes by inputting linear acceleration and gyro data [31]. These 3D pose changes, when combined with the initial pose, can represent a 3D trajectory. However, when utilizing this method, the error in the estimated orientation diverged with an increase in the estimation time. Therefore, a method to stabilize the orientation change estimation performance was required. The extended IONet proposed incorporating additional inputs of gravitational acceleration and geomagnetic data, which are directly related to orientation, as well as introducing a network to extract multidimensional features from gravitational acceleration [32]. The approach significantly reduced trajectory and orientation errors. However, orientation still diverges as the estimation time increases. DO IONet overcomes these limitations by directly estimating the orientation in the reference coordinate system [33]. It does not require an initial orientation and avoids drift errors because only the orientation values are utilized. Consequently, it exhibits consistent 3D translation vector estimation performance, even with longer estimation periods.
3. Extended Direct Orientation Inertial Odometry Network
This section presents the proposed transformer-based extended DO IONet to enhance the trajectory-tracking performance. The proposed method operates within the DO IONet framework, comprising encoding and decoding steps. Data obtained from the 9-axis IMU were compressed in the encoding step. Time-series data were processed in the decoding step to output the position change and orientation. Subsequently, the calculated 3D translation vector was integrated to generate the trajectory by utilizing the position change and orientation. Various experiments were performed to design the most suitable encoder and decoder for inertial data. These experiments optimized the performance and effectiveness of the proposed method to estimate the trajectory and orientation from inertial data.
3.1 Direct Orientation Inertial Odometry Framework
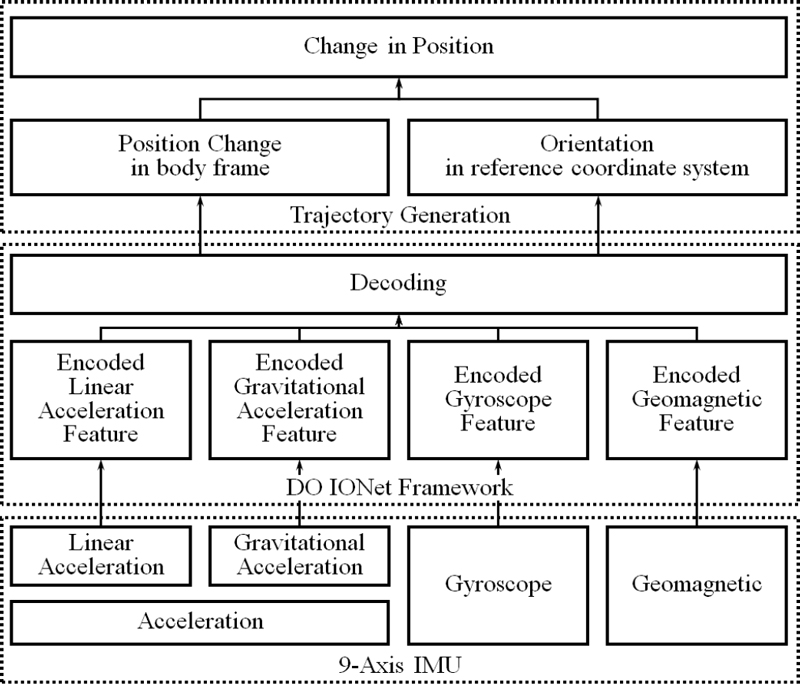
As shown in Figure 3, the DO IONet framework comprised an encoder to extract local features and a decoder for sequential data processing. The encoder aimed to reduce the complexity of inertial data and prevent overfitting. The decoder extracted the complete pattern by incorporating temporal dependencies into the features. It served as a connector that linked each time-step feature to regress to a pose.
The direct orientation IO framework overcame the drift error associated with orientation estimation and accurately estimated position change and orientation in the reference coordinate system. This framework, similar to the DO IONet, comprised an encoder to extract local features and a decoder for sequential data processing. The encoder decreased the complexity of the inertial data and prevented over-fitting, whereas the decoder captured temporal dependencies in the features, enabling them to effectively regress to a relative position for each time step.
3.2 Network Architecture
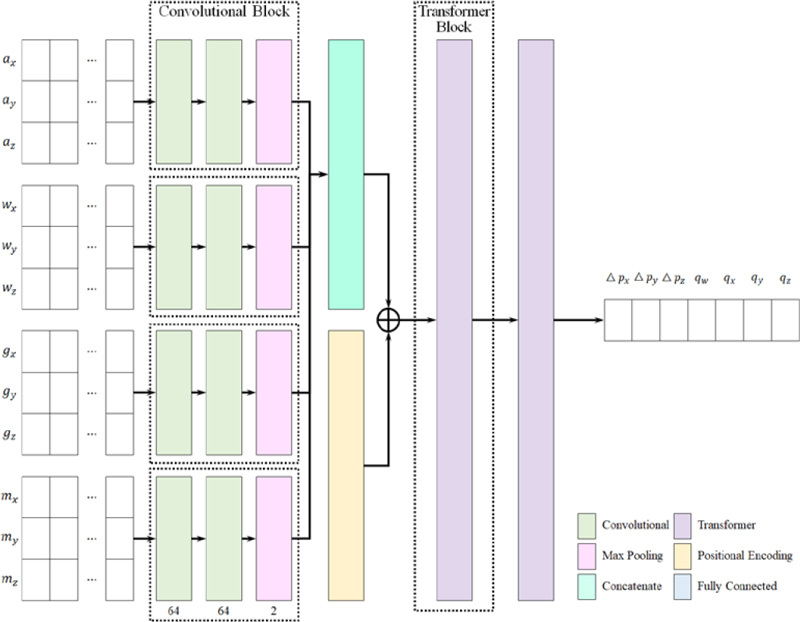
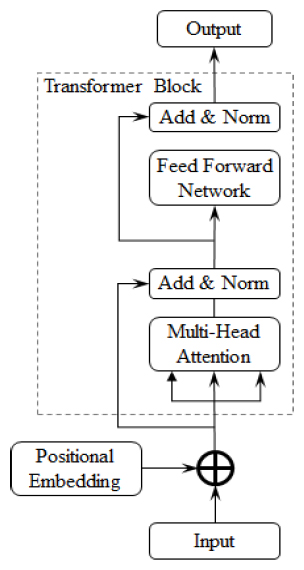
The architecture of the proposed network, which inputs four types of inertial data in a time-series format and outputs position changes and orientation is shown in Figure 4. The four types of inertial data include linear acceleration (a), angular velocity (w), gravitational acceleration (g), and geomagnetic value (m). One set of input data contained 200 inertial data points measured over a duration of 2 s. The position change △p was the velocity between the 95th and 105th data points within the body frame. q was the orientation at the 95th frame in the reference coordinate system, and quaternions were utilized instead of Euler angles, which had limited angular representation ranges, for learning convenience. The proposed network comprised a convolutional block as an encoder, a transformer block, and fully connected layers as decoders.
The convolutional block comprised two convolutional layers and one max-pooling layer. It compressed the local features of inertial data to reduce complexity. Each compressed feature was concatenated and combined with a positional vector for sequential data processing in the transformer block. The transformer block comprised two layers, each of which employed multi-head attention and a feedforward network, as shown in Figure 5. The transformer captured the relative importance and context of the compressed features and functioned as a decoder, connecting each time-step feature for regression. Finally, △p and q were output by utilizing a fully connected layer. Subsequently, q, transformed by the rotation matrix along with △p , was multiplied to generate the trajectory over a unit of time, which is the 3D translation vector.
3.3 Six-DOF Relative Pose Representation
The current position pt, previous position pt-1, orientation R(qt-1), and position change △p were utilized to represent the pose changes in the reference coordinate system. △p indicates the value in the body frame. The 3D translation vector was determined by multiplying the previous orientation with △p. Orientation calculations adopted a unit quaternion because the network could not learn by utilizing Euler angles. The current position can be calculated as follows:
| (1) |
where pt represents the current position, which is the sum of the previous position and the 3D translation vector. It provides a concise pose representation and structurally reduces drift errors by utilizing the DO IONet framework, which directly estimates the orientation.
3.4 Loss Function
The 6-DOF IONet designed a loss function for independent position values along the three axes and dependent direction values for the four quaternion vectors. The consideration of the homoscedastic uncertainty for each task is necessary due to the different scales of position and orientation. Therefore, a multitask loss was adopted to learn various quantities at different scales [34].
| (2) |
where σi and Li denote the variance and loss functions of the ith, respectively. To prevent a division by zero within the total loss, the utilization of exponential mapping removed constraints on scalar values, and the incorporation of log variance enhanced network stability.
Two loss functions were utilized, as expressed in Equation (3).
| (3) |
where LDPMAE and LQME represent the delta position mean absolute error and quaternion multiplicative error, respectively.
| (4) |
| (5) |
where LDPMAE and LQME denote the loss functions associated with the displacement of the sensor unit within the body frame and the orientation within the reference coordinate system, respectively. △imag(q) resulted in a complex number being treated as a real number. Meanwhile, the ⊗ represents the Hamilton product operator, signifying the addition of two angles that indicate the complex conjugate of q.
4. Experiment
4.1 Dataset
Experiments were conducted by utilizing OxIOD, which provides four types of inertial data. Inertial data from OxIOD were captured by utilizing an iPhone 7 and the ground truth for pose was established by utilizing the Vicon motion capture system [27]. OxIOD offers four different form factors based on how the device is transported: handheld, pocket, handbag, and trolley. We utilized the handheld case in our experiments, which provided the longest data collection time and distance. The handheld case comprised 24 sequences. We discarded the initial 12 s and the final 3 s of each sequence to eliminate errors in the Vicon motion capture system and facilitate a clear comparison with existing models. Furthermore, during OxIOD training, we mitigated an error of approximately 1% that occurred when the standard deviation of the difference between consecutive frames and orientations reached 20°. In testing, data with errors were incorporated for comparison with other models. In total, 54,885 training samples were employed.
4.2 Training
The core libraries utilized for training included Tensorflow 2.4.1, Keras 2.4.3, tfquaternion 0.1.6, and numpy-quaternion 2022.4.2. We employed an Adam optimizer with a learning rate of 0.0001 to converge the loss function. The batch size was set to 32 and training ran for 500 epochs. A validation data ratio of 10% was utilized to monitor the training progress. Our model was trained by utilizing an NVIDIA RTX 6000 GPU.
4.3 Evaluation
Data were divided into 17 training and 7 testing datasets. The model was evaluated from various perspectives by utilizing short- and long-term data. The evaluation criteria included the trajectory, orientation, and 3D translation vectors. For short-term data evaluation, time intervals from 0 s to 20 s and from 100 s to 120 s were utilized for each test data sequence. For long-term data evaluation, the time intervals ranged from 0 s to 100 s and from 100 s to 200 s for each sequence. Although the trajectory provided insights into the performance across various instances, it contained cumulative errors from continuous integration, making it less suitable to evaluate the performance of the model over a specific unit of time. Therefore, orientation and 3D translation vectors were utilized as evaluation metrics for the performance assessment per unit of time. Two existing approaches to estimate position and orientation changes were evaluated and compared with the DO IONet framework. For the DO IONet experiments, eight evaluations were performed based on different encoder and decoder configurations. Three evaluations were performed on the models designed by utilizing stacking transformers. Overall, the evaluations encompassed a comprehensive analysis of various approaches to estimate the position and orientation changes, including two existing methods and multiple configurations of the DO IONet framework.
5. Results and Discussion
5.1 Evaluation of short-term inertial data
Short-term evaluations were performed by utilizing data from 0–20 s and 100–120 s. The average trajectory, orientation, and 3D translation root-mean-square errors (RMSEs) at these two time points are listed in Table 1. The models that estimated the trajectory and 3D translation vector exhibited superior performance in the estimation of position and orientation change. However, for the orientation, the extended DO IONet with one convolutional block and two transformers outperformed the others.
Experiments with different numbers of convolutional blocks were performed to reduce the feature size input to the decoder that processed the time-series data. Based on the results, the model performed better when only one convolutional block was utilized, regardless of the decoder type. This is because the pooling layer within the convolutional block could omit essential details in the feature representation. Furthermore, experiments were performed with IONet models comprising only stacked transformers without a separate encoder. The performance improved as the number of stacked transformers increased. A model with three layers of transformers demonstrated a performance close to that of the extended DO IONet.
5.2 Evaluation of long-term inertial data
The long-term evaluation results for each model are listed in Table 2. The RMSE of the trajectory included errors from previous time points as the estimation time increased, resulting in divergence for all IONet models. The orientation RMSE of existing frameworks diverged because they relied on the integration of the initial values to output the final pose. However, the models that utilized the DO IONet framework exhibited values similar to those of the short-term results. Consequently, based on the 3D translation vector, calculated as the product of the position change and orientation, models that utilized the novel framework with accurate orientation values generally performed better.
In the case of the encoder, as demonstrated by the previous results, missing features and higher errors resulted from the stacking of additional convolutional blocks. Some models that only comprised transformers experienced increased errors despite being more stacked. In the long-term evaluation, the 9-axis IONet exhibited the lowest trajectory RMSE. However, the RMSE of the extended DO IONet orientation was approximately 73% and 11% lower than that of the 9-axis IONet and DO IONet, respectively. Furthermore, the RMSE of the extended DO IONet 3D translation vector was approximately 53% and 5% lower than that of the 9-axis IONet and DO IONet, respectively.
5.3 Discussion
The existing IONet and proposed DO IONet frameworks exhibited different characteristics. The existing frameworks continuously integrated changes from the initial position and orientation, resulting in relatively small trajectory estimation errors in the short term. However, the 3D translation vector diverged owing to uncorrectable orientation errors after several tens of seconds. Therefore, although existing frameworks were utilized for short-term trajectory estimation with a single IMU, they did not fully exploit the advantages of IMUs in small-scale odometry for orientation estimation. Conversely, the DO IONet framework also estimated position changes; however, the orientation was output in the reference coordinate system. This enabled relative position estimation regardless of the current orientation, provided the initial position was known. Consequently, it can be utilized as part of a sensor-fusion odometry system or as a complementary metric for the current pose. Therefore, the DO IONet framework offered high scalability and flexibility, making it effective for various practical applications.
We conducted experiments to determine the optimal design for the encoder and decoder within the DO IONet framework. For the encoder, we investigated performance based on the number of convolutional blocks, with each block comprising two convolutional layers. Models with only one convolutional block outperformed those with two blocks, indicating that excessive convolutional layers could diminish sequential features. We examined the performance of different decoders, including LSTM, GRU, one transformer, and two transformers. Models with transformer blocks, commonly utilized for feature extraction in time-series data, demonstrated improved performance regardless of the estimation time. This suggests that transformers can be stacked to enhance performance and serve as a viable alternative to recurrent networks. Finally, we examined performance based on the number of transformers to determine whether the performance improved by increasing the number of stacked transformers. Models with two transformer blocks outperformed those with only one, whereas the performance difference between models with three stacked transformers and those with two stacked transformers was minimal.
6. Conclusion
This study proposed an extended DO IONet that improved the estimation performance of the orientation and 3D translation vectors. Experiments were performed with two encoders based on the depth of the convolutional blocks and four decoders for sequential data learning to design the optimal model within the DO IONet framework. Moreover, experiments were performed with stacked transformers to improve the pose estimation performance. The strengths and weaknesses of existing frameworks and the proposed DO IONet framework were compared experimentally by considering three evaluation metrics.
The proposed model could be integrated with a camera, LiDAR, and other multisensory odometry systems to enhance the pose estimation performance and convenience. Moreover, it could be utilized to improve navigation systems, such as the GPS, for large-scale navigation. Studies on large-scale navigation, such as the GPS and indoor navigation systems, have continuously improved and offered high precision, small-scale navigation systems, such as the proposed DO IONet system. However, these systems require expensive equipment and often involve ambiguous evaluation criteria. Studies on detailed operational validation and measurement-related technologies are limited for problems in commercial applications. These technologies, including the proposed approach, are expected to be commercialized in the future by providing robot-assisted services in healthcare, medical devices, cooking, and other expert services. Therefore, this study explored precise motion estimation based on cameras and multiple IMUs to acquire data similar to the manner in which humans perceive positional changes in the environment.
Acknowledgments
This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant RS-2021-KA162922).
Author Contributions
Conceptualization, H. I. Seo; Methodology, Y. S. Han; Software, Y. S. Han; Validation, Y. S. Han and M. J. Kim; Formal Analysis, Y. S. Han; Investigation, Y. S. Han; Resources, M. J. Kim; Data Curation, M. J. Kim; Writing—Original Draft Preparation, Y. S. Han; Writing—Review & Editing, H. I. Seo; Visualization, M. J. Kim; Supervision, D. H. Seo; Project Administration, H. I. Seo; Funding Acquisition, D. H. Seo.
References
-
J. Wendel, O. Meister, C. Schlaile, and G. F. Trommer, “An integrated GPS/MEMS-IMU navigation system for an autonomous helicopter,” Aerospace Science and Technology, vol. 10, no. 6, pp. 527-533, 2006.
[https://doi.org/10.1016/j.ast.2006.04.002]

-
J. H. Seong and D. H. Seo, “Selective unsupervised learning-based Wi-Fi fingerprint system using autoencoder and GAN,” IEEE Internet of Things Journal, vol. 7, no. 3, pp. 1898-1909, 2020.
[https://doi.org/10.1109/JIOT.2019.2956986]

-
J. H. Seong and D. H. Seo, “Environment adaptive localization method using Wi-Fi and Bluetooth low energy,” Wireless Personal Communications, vol. 99, pp. 765-778, 2018. .
[https://doi.org/10.1007/s11277-017-5151-x]

-
S. A. Mohamed and M. H. Haghbayan, T. Westerlund, J. Heikkonen, H. Tenhunen, and J. Plosila, “A survey on odometry for autonomous navigation systems,” IEEE access, vol. 7, pp. 97466-97486, 2019.
[https://doi.org/10.1109/ACCESS.2019.2929133]

-
N. Yang, L. V. Stumberg, R. Wang, and D. Cremers, “D3vo: Deep depth, deep pose and deep uncertainty for monocular visual odometry,” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 1278-1289, 2020.
[https://doi.org/10.1109/CVPR42600.2020.00136]

-
A. A. Deraz, O. Badawy, M. A. Elhosseini, M. Mostafa, H. A. Ali, and A. I. El-Desouky, “Deep learning based on LSTM model for enhanced visual odometry navigation system,” Ain Shams Engineering Journal, vol. 14, no. 8, p. 102050, 2023. .
[https://doi.org/10.1016/j.asej.2022.102050]

-
Y. Zhou, G. Gallego, and S. Shen, “Eventbased stereo visual odometry,” IEEE Transactions on Robotics, vol. 37, no. 5, pp. 1433-1450, 2021. .
[https://doi.org/10.1109/TRO.2021.3062252]

-
R. Duan, D. P. Paudel, C. Fu, and P. Lu, “Stereo orientation prior for UAV robust and accurate visual odometry,” IEEE/ASME Transactions on Mechatronics, vol. 27, no. 5, pp. 3440-3450, 2022.
[https://doi.org/10.1109/TMECH.2022.3140923]

-
J. Zhang and S. Singh, “Low-drift and real-time lidar odometry and mapping,” Autonomous Robots, vol. 41, pp. 401-416, 2017.
[https://doi.org/10.1007/s10514-016-9548-2]

- Q. Li, S. Chen, C. Wang, X. Li, C. Wen, M. Cheng, and J. Li, “Lo-net: Deep real-time lidar odometry,” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8465-8474, 2019. .
-
P. Dellenbach, J. E. Deschaud, B. Jacquet, and F. Goulette, “CT-ICP: Real-time elastic LiDAR odometry with loop closure,” In 2022 International Conference on Robotics and Automation (ICRA), pp. 5580-5586, 2022.
[https://doi.org/10.1109/ICRA46639.2022.9811849]

-
Y. S. Park, Y. S. Shin, and A. Kim, “PhaRaO: Direct radar odometry using phase correlation,” In 2020 IEEE International Conference on Robotics and Automation (ICRA), pp. 2617-2623, 2020.
[https://doi.org/10.1109/ICRA40945.2020.9197231]

-
D. Adolfsson, M. Magnusson, A. Alhashimi, A. J. Lilienthal, and H. Andreasson, “CFEAR radarodometry - Conservative filtering for efficient and accurate radar odometry,” In 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 5462-5469, 2021.
[https://doi.org/10.1109/IROS51168.2021.9636253]

-
P. C. Kung, C. C. Wang, and W. C. Lin, “A normal distribution transform-based radar odometry designed for scanning and automotive radars,” In 2021 IEEE International Conference on Robotics and Automation (ICRA), pp. 14417-14423, 2021.
[https://doi.org/10.1109/ICRA48506.2021.9561413]

-
S. Y. Cho and C. G. Park, “A calibration technique for a two-axis magnetic compass in telematics devices,” ETRI Journal, vol. 27, no. 3, pp. 280-288, 2005. .
[https://doi.org/10.4218/etrij.05.0104.0192]

- A. A. A. Rahni and I. Yahya, “Obtaining translation from a 6-DOF MEMS IMU—An overview,” In 2007 Asia-Pacific Conference on Applied Electromagnetics, pp. 1-5, 2007.
-
X. Chen, C. Shen, W. B. Zhang, M. Tomizuka, Y. Xu, and K. Chiu, “Novel hybrid of strong tracking Kalman filter and wavelet neural network for GPS/INS during GPS outages,” Measurement, vol. 46, no. 10, pp. 3847-3854, 2013.
[https://doi.org/10.1016/j.measurement.2013.07.016]

-
S. Y. Cho and W. S. Choi, “Robust positioning technique in low-cost DR/GPS for land navigation,” IEEE Transactions on Instrumentation and Measurement, vol.55, no.4, pp. 1132-1142, 2006.
[https://doi.org/10.1109/TIM.2006.877718]

-
P. G. Savage, “Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms,” Journal of Guidance, Control, and Dynamics, vol. 21, no. 1, pp. 19-28, 1998.
[https://doi.org/10.2514/2.4228]

-
P. G. Savage, “Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms,” Journal of Guidance, Control, and dynamics, vol. 21, no. 2, pp. 208-221, 1998.
[https://doi.org/10.2514/2.4242]

-
W. Gao, J. Li, G. Zhou, and Q. Li, “Adaptive Kalman filtering with recursive noise estimator for integrated SINS/DVL systems,” The Journal of Navigation, vol. 68, no. 1, pp. 142-161, 2015.
[https://doi.org/10.1017/S0373463314000484]

-
Z. Zheng, S. Han, and K. Zheng, “An eight-position self-calibration method for a dual-axis rotational inertial navigation system,” Sensors and Actuators A: Physical, vol. 232, pp. 39-48, 2015. .
[https://doi.org/10.1016/j.sna.2015.05.002]

-
W. Kang and Y. Han, “SmartPDR: Smartphone-based pedestrian dead reckoning for indoor localization,” IEEE Sensors Journal, vol. 15, no. 5, pp. 2906-2916, 2015. .
[https://doi.org/10.1109/JSEN.2014.2382568]

-
X. Hou and J. Bergmann, “Pedestrian dead reckoning with wearable sensors: A systematic review,” IEEE Sensors Journal, vol. 21, no. 1, pp. 143-152, 2021. .
[https://doi.org/10.1109/JSEN.2020.3014955]

-
X. Chen, X. Zhang, M. Zhu, C. Lv, Y. Xu, and H. Guo, “A novel calibration method for tri-axial magnetometers based on an expanded error model and a two-step total least square algorithm,” Mobile Networks and Applications, vol. 27, no. 2, pp. 794-805, 2022.
[https://doi.org/10.1007/s11036-021-01898-z]

-
H. Yan, Q. Shan, and Y. Furukawa, “RIDI: Robust IMU double integration,” In Proceedings of the European Conference on Computer Vision (ECCV), pp. 641-656, 2018. .
[https://doi.org/10.1007/978-3-030-01261-8_38]

- C. Chen, P. Zhao, C. X. Lu, W. Wang, A. Markham, and N. Trigoni, “Oxiod: The dataset for deep inertial odometry,” arXiv preprint arXiv:1809.07491, 2018.
-
C. Chen, C. X. Lu, J. Wahlström, A. Markham, and N. Trigoni, “Deep neural network based inertial odometry using low-cost inertial measurement units,” IEEE Transactions on Mobile Computing, vol. 20, no. 4, pp. 1351-1364, 2021.
[https://doi.org/10.1109/TMC.2019.2960780]

-
C. Chen, P. Zhao, C. X. Lu, W. Wang, A. Markham, and N. Trigoni, “Deep-learning-based pedestrian inertial navigation: Methods, data set, and on-device inference,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4431-4441, 2020. .
[https://doi.org/10.1109/JIOT.2020.2966773]

-
M. Zhang, M. Zhang, Y. Chen, and M. Li, “IMU data processing for inertial aided navigation: A recurrent neural network based approach,” In 2021 IEEE International Conference on Robotics and Automation (ICRA), pp. 3992-3998, 2021.
[https://doi.org/10.1109/ICRA48506.2021.9561172]

-
J. P. Silva do Monte Lima, H. Uchiyama, and R. I. Taniguchi, “End-to-end learning framework for IMU-based 6-DOF odometry,” Sensors, vol. 19, no. 17, p. 3777, 2019.
[https://doi.org/10.3390/s19173777]

-
W. Y. Kim, H. I. Seo, and D. H. Seo, “Nine-Axis IMU-based extended inertial odometry neural network,” Expert Systems with Applications, vol. 178, p. 115075, 2021. .
[https://doi.org/10.1016/j.eswa.2021.115075]

-
H. I. Seo, J. W. Bae, W. Y. Kim, and D. H. Seo, “DO IO-Net: 9-axis IMU-based 6-DOF odometry framework using a neural network for direct orientation estimation,” IEEE Access, vol. 11, pp. 55380-55388, 2023.
[https://doi.org/10.1109/ACCESS.2023.3281970]

- A. Kendall, Y. Gal, and R. Cipolla, "Multi-task learning using uncertainty to weigh losses for scene geometry and semantics,” In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7482-7491, 2018.