Improved Adaptive Smoothing Filter for Indoor Localization Using RSSI
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the indoor location estimation system, which has recently been actively studied, the received signal strength indicator contains a high level of noise when measuring the signal strength in the range between two nodes consisting of a receiver and a transceiver. To minimize the noise level, this paper proposes an improved adaptive smoothing filter that provides different exponential weights to the current value and previous averaged one of the data that were obtained from the nodes, because the characteristic signal attenuation of the received signal strength indicator generally has a log distribution. The proposed method can effectively decrease the noise level by using a feedback filter that can provide different weights according to the noise level of the obtained data and thus increase the accuracy in the distance and location without an additional filter such as the link quality indicator, which can verify the communication quality state to decrease the range errors in the indoor location recognition using ZigBee based on IEEE 802.15.4. For verifying the performance of the proposed improved adaptive smoothing filter, actual experiments are conducted in three indoor locations of different spatial sections. From the experimental results, it is verified that the proposed technique is superior to other techniques in range measurement.
Keywords:
Indoor location estimation system, Signal strength indicator, Link quality indicator, ZigBee, Improved adaptive smoothing filter1. Introduction
As information and communication technology (ICT) develops, wireless sensor networks (WSNs) that can provide necessary information irrespective of the time and place enrich the human life. In particular, a location-based system (LBS) providing many advantages by obtaining the object locations in real time has been widely applied in various fields such as medicine, mobiles, and agriculture [1]-[5]. The LBS can largely be classified into outdoor and indoor environments. While the outdoor environment has made considerable progress using the global positioning system (GPS), which can identify locations using various satellite signals, the indoor environment implements indoor localization using wireless communication such as Wi-Fi [6]-[8], ZigBee [9][10], radio frequency identification (RFID) [11], ultra wide band (UWB) [12]-[14], and chirp spread spectrum (CSS) [15][16] because it is difficult to receive the GPS signals. It is more difficult to establish the LBS in the indoor environment, where more disturbances exist when compared with the outdoor environment because the radio-wave signals can be easily distorted by spatial forms, obstacles, electronic equipment, etc. Nevertheless, various methods have been studied to implement the indoor LBS, represented by the time of arrival (ToA), time difference of arrival (TDoA), angle of arrival (AoA), and received signal strength indicator (RSSI) [17]-[26]. Although the method that measures the range using the time during the propagation of radio waves such as UWB and CSS has a relatively accurate performance, it is either commercially unavailable or unaffordably expensive because the RSSI, which forms the basis for the localization method using the received radio-wave signal strength, is supported in most wireless communications, and the indoor LBS can be economically implemented by using the already established Wi-Fi, Bluetooth, and ZigBee.
Consequently, various studies have been accomplished to improve the indoor localization performance using the RSSI. In particular, although the RSSI-based fingerprint method that applies in mobile devices has the advantage of localization in a non-line of sight (NLOS) environment where the radio waves cannot directly propagate because of the physical obstacles, the training process, in which radio maps should be established beforehand in the respective locations to be localized using the RSSI, is required, and it is difficult to implement an accurate localization performance because of the range errors having a few meters[27][28]. Also, because noises are easily included in the RSSI-based localization by disturbances such as multipath and electronic equipment, the filtering methods for reducing these noise problems has been studied [29][30]. These methods reduce the ranging errors by fusing the link quality indicator (LQI) values that represent the metric of the current quality of the received signal, as well as the RSSI and provide weights for noise elimination. However, these methods have the disadvantage that because the LQI and RSSI filters are respectively applied, the processing time becomes longer, and the LQI is not provided in Wi-Fi, which has recently been used as the most general-purpose communication network.
In order to overcome this disadvantage and to measure the more accurate range, this paper proposes the improved adaptive smoothing filter (IASF), which can effectively eliminate the noises by providing exponential weights to the acquired data in consideration of the signal attenuation characteristics of the RSSI with a log distribution. The proposed method uses the feedback filter, which can provide different weights to the current value and previous averaged value according to the noise level included in the obtained signals, and applies fitted weights using an exponential function so as to be appropriate to RSSI-based localization in the indoor environment.
Consequently, the proposed method can increase the estimated range accuracy even without an additional filter such as the LQI, which reduces the distance errors using ZigBee based on IEEE 802.15.4. For verifying the IASF performance, after measuring the RSSI from 0 (m) to 10 (m) using two ZigBee-based wireless nodes in three different indoor sections which consist of half-open, open, and closed section, experiments are accomplished using the proposed method. It is verified that the simple filtering process of proposed method can facilitate the development of the LBS. In addition, this technique can be used as an effective preprocessing step to implement the RSSI-based localization as well as improve the performance of noise elimination compared with the other existing methods.
2. Related Theory
2.1 RSSI
RSSI, which indicates the received radio-wave signal strength between the nodes, is supported in most wireless standards; therefore, it can be provided with the communication chipsets. The general radio-frequency (RF) chipsets can transmit signals of approximately -90 dBm to 0 dBm. The signal strength of less than -75 dBm is determined to be low because signals have high packet loss rates, and the signal strength is determined to be high when the RSSI is greater than -25 dBm because there are a few cases where the radio waves that are lost by the mediums are received at 0 dBm. The RSSI values in the free space are expressed as the logarithm model in Equation (1) as follows.
| (1) |
where n is the signal attenuation constant which depends on the medium; d is the distance (unit: meter) from the signal source to the receiving node; and A, representing the offset, is the RSSI value measured at 1m distance. The CC2420 chipset used in this study is obtained by averaging the received signals in eight symbol periods (128 μs) and provided as a signed 8-bit value. When -45 is added to this value, we can obtain the RSSI in dBm [31].
2.2 LQI
LQI, which represents the received characteristic packet quality according to the communication state, is included in the IEEE 802.15.4 standard and defined as an unsigned 8-bit (0–255) value. The increasing LQI value represents the smoother communication state, and the increasing signal strength represents the lower package loss rate proportional to the RSSI.
The CC2420 chipset, which is widely used in ZigBee communication, provides the correlation values of 50–110 after examining the eight symbols of the received packet, and these correlation values are determined to represent the high quality and low quality when greater than 108 and less than 105, respectively. The CC2420 datasheet mentions that the values of 50~110 should be converted into values of 0~255 from Equation (2)[31].
| (2) |
where CORR represents the correlation values (50–110) provided by the chipset, and a and b are the constants to convert the range. The values a and b should be selected on the basis of the user’s experience because different correlation values are output according to the communication environment.
3. Experimental Testbed
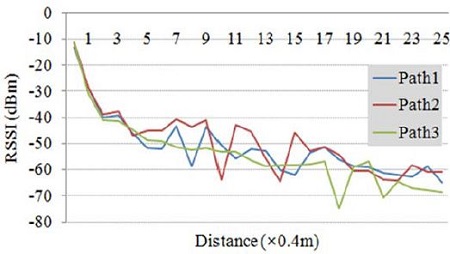
The purpose of this study is to minimize the range errors for improving the RSSI-based indoor localization performance and to verify this by experiments in the indoor environment. Consequently, the RSSI was measured from 0 m to 10 m using two ZigBee (CC2420) nodes based on IEEE 802.15.4 in three respective paths of different forms. The experiments were conducted in the corridors and stairs of the first and third floors of the College of Engineering 1 building of Korea Maritime and Ocean University, and the structural drawings of the respective places are shown in Figure 1. Figure 1 (a), which is half-open section, has the stairs on the right side of the path, Figure 1 (b), which is closed section, is in the general corridor environment in which concrete walls and a door exist, and Figure 1(c), is the path going up the stairs. The RSSI and LQI of two nodes were measured at an interval of 0.4 m, and the results are shown in Figure 2 and 3. In Figure 2, which shows the RSSI according to the distance measured in the three locations, the x-axis represents the distance between the two nodes, and the y-axis, the obtained RSSI. We can verify that the increasing signal strength becomes more similar to the form of a log model, and the decreasing signal strength is more distorted because more noises are included. We can observe that although the signal strength is approximately -10 dBm and -65 dBm on average at the distances between the two nodes of 0 m and 10 m, respectively, as the signal strength decreases to less than -40 dBm, the graph becomes very irregular and many noises are mixed. For correcting the distorted signals by these noises, Equation (1) is redefined as Equation (3) by adding the scaling factor(s) to it, and thus, the distance between the two nodes (d) is expressed as Equation (4).
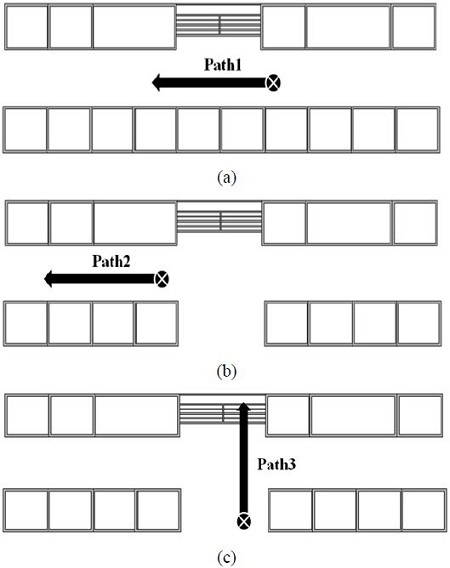
Experimental indoor environment of (a) half-open section (path 1), (b) closed section (path 2), and (c) open section (path 3).
| (3) |
| (4) |
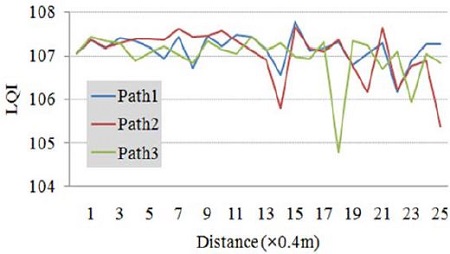
Figure 3 shows the LQI, which represents the communication quality between the two nodes in the three paths, the x-axis represents the distances between the nodes, and the y-axis represents the obtained LQI values. We can verify that although the communication state is generally good in the range of the measured LQI values of approximately 105~108, as the distance between the two nodes increases, there is great variation in the LQI values, thereby gradually lowering the communication quality. The ZigBee communication node used for these experiments is ZigbeX developed by Hanback Electronics Co., Ltd. This product enables wireless communication using the CC2420 chipset, and the RSSI between the two nodes was measured with the radio waves set to be transmitted at the maximum transmission output of 0 dBm at the transmitter of this module. The TinyOS specialized in the sensor network was used to effectively control the hardware of the respective nodes, and the MATLAB program was used to verify the result of application of the noise elimination filter to the obtained RSSI.
4. System Implementation Using Filter
Wireless signals in the indoor environment include noises because they are easily distorted by various disturbances such as spatial structure, quality of the material, and electronic equipment and the range errors can be reduced by using several filters. Reduction of range errors is a very important process for accurate estimation of the locations of objects, which is the main objective of the indoor localization.
4.1 Feedback filter
The feedback filters used for eliminating noises in various fields are basically used as the LQI, RSSI, BOTH, and proposed filters, which are referred to in this study, and can be expressed as Equation (5)
| (5) |
where α represents the weighted value, x represents the most recently measured value, and represents the previous averaged value. The feedback filter obtains the average by providing the distributed weights to the most recently measured and previous averaged values. The range of the value is 0~1, and as the value approaches 1, the proportion of the most recently measured value is increased, and as the value approaches 0, that of the previous averaged value is increased. Consequently, although it is advantageous to design in such a manner that the more noises the signals include, the nearer to 0 the values are, the performance can deteriorate because of improper reflection of the current state. In other words, the values decisively affect the filtered output values; therefore, these values should be selected in accordance with the signal model obtained from the system.
4.2 LQI, RSSI, and BOTH filters
The LQI filter, in which the values depend on the obtained LQI, is expressed as Equation (6). The value approaches 0.8 to increase the proportion of the most recently measured values because the larger the LQI values are, the better the communication quality is. When the obtained LQI is greater than 100, the range of the value is 0.2~0.8, and when it is less than 100, the communication quality is very poor, and the determined value is 0.
| (6) |
Equation (7), which represents the RSSI filter, determines the proportions of the most recently measured and previous averaged values because the values depend on the obtained RSSI sizes. The range of the RSSI input in this filter is from -75 to -15 dBm, and that of the value is 0.5~1. The lesser the received signal strength is, the higher is the probability that the noise components are included, the value is determined to be near 0.5, and the proportion of the most recently measured values decreases.
| (7) |
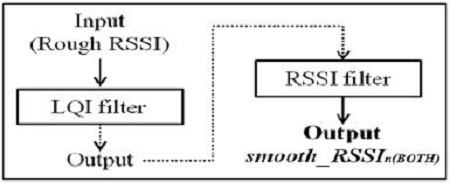
The BOTH filter, which eliminates noises by using both LQI and RSSI filters, is illustrated in Figure 4. The noises of the obtained rough RSSI signals are primarily eliminated by the LQI filter as in Equation (6), and these first resulting values are used as the input values to the RSSI filter. The second resulting values, the noises of which are secondarily eliminated by the RSSI filter as in Equation (7), are the final output of the BOTH filter. Similarly, the BOTH filter reduces the noise level by performing two filtering processes.
4.3 Proposed improved adaptive smoother filter
In order to improve above mentioned techniques, the proposed method reduces the range errors by effectively eliminating the noises in the rough RSSI signals. Consequently, we propose the IASF that is much improved when compared with the previously mentioned LQI, RSSI, and BOTH filters, and this filter is expressed as Equation (8).
| (8) |
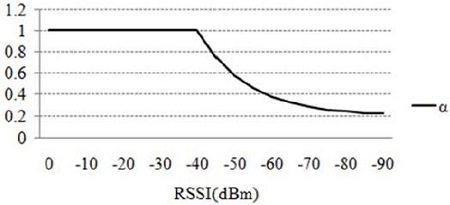
In the proposed IASF using the feedback filter in which the determination of values is a key, the values are determined by using an exponential function to effectively reduce noises acquired from RSSI. The ranges and characteristics of the values determined in this manner are represented as in Figure 5, and while the obtained RSSI is greater than -40 dBm, the value is 1, and when it is less than -40 dBm, the value decreases until ≒ 0.2. Here, the reason for the threshold value to be -40 dBm is that when the RSSI is greater than approximately -40 dBm, the reliability is very high as shown in Figure 2. The RSSI range, in which the CC2420 chipsets used in the experiments are transmitted in the actual environment, is from -90 dBm to -10 dBm, and 0 ≒ exp(-6); therefore, the resulting values are adjusted by multiplying (RSSI+40) by 0.075 = (-6)/(-80). Whereas the input signal strength is approximately -90 dBm and various noise components are included, the minimum value should be more than 0.2 in order to increase the proportion of the recently measured values by at least greater than 20%.
5. Experimental Performance
For verifying the IASF performance for eliminating noise components, experiments were conducted in three locations of different spatial structures. The proposed IASF, which provided the different weights using the feedback filter with an exponential function, improves the noise elimination performance when compared with the existing LQI, RSSI, and BOTH filters. Figure 6, which shows the graphs comparing the proposed IASF performance and those of the existing three filters, represents the errors in the estimated distances using the RSSI obtained according to the actual distances between the two nodes. In the experimental results in Figure 6 (a), which is the half-open section indoor environment, the noise levels are estimated to rapidly have increased because the stairs are located on the right side 5~6 m from the starting point, and here, the proposed IASF effectively reduces the noise levels. Similarly, as shown in Figure 6 (b) and (c), we can verify that the IASF definitely reduces the noise level at the points where the noise levels rapidly increased. This implies that because the IASF has excellent noise elimination performance when estimating the range using the RSSI, it can be usefully used as a preprocessing step in the indoor localization. For a more detailed performance comparison, the average errors of respective filters in m and the improved rates of the filters versus the no filter are listed in Table 1. We can verify that the proposed IASF, BOTH, RSSI, and LQI filters are sequentially excellent in the noise elimination performance in the three paths. The IASF most effectively reduces the maximum error size as well as the average error size, and particularly in Path 3 going up the stairs, it improves the performance by 62% in the average error and 77% in the maximum error. This verifies that the IASF can be more effectively used in poor environments such as Path 3, which has the possibly most severe radio-wave disturbances among the three paths because of the inclined stairs of scores of steps and irregular left and right sections.
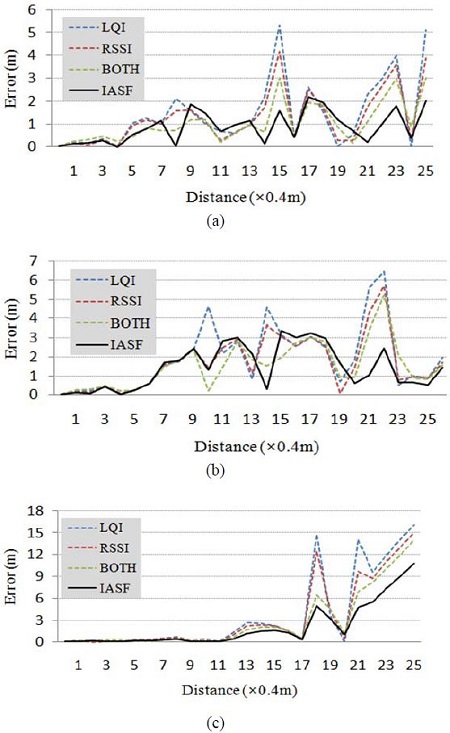
Performance results of different methods with various filters in (a) path 1, (b) path 2, and (c) path 3.
Abbreviations above are presented as path (P), the used filter (F), the average error (AE), the improvement rate of AE (AEIR), the maximum error (ME), the improvement rate of ME (MEIR). respectively and the parentheses indicate units
6. Conclusion
In this paper, when measuring the range between the two nodes to identify the locations of objects in the indoor environment, to effectively eliminate the noises included in the RSSI, the IASF, which provides different exponential weights to the current value and previous averaged value, was proposed. For verifying the proposed filter performance, experiments were conducted in three different paths, and the noise elimination performance was improved in all the paths, and particularly in the places where the most noises occurred, the proposed filter showed the best performance by 13% in the average errors and by 7% in the maximum errors when compared with the existing filters. Furthermore, the IASF does not require an additional filter such as the LQI filter; therefore, its simplified noise elimination process facilitates the development of the LBS, and it is very flexible technique which can be applied in various wireless communications such as Wi-Fi, UWB, and RFID as well as ZigBee based on IEEE 802.15.4. These results imply that the IASF can be used as a preprocessing step that exhibits excellent noise elimination performance in various indoor LBSs using the RSSI.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (No. 2014R1A1A4A01008081).
This paper is extended and updated from the short version that appeared in the Proceedings of the International Symposium on Marine Engineering and Technology (ISMT 2014), held at BEXCO, Busan, Korea on October 17-19, 2014.
References
-
H. Alemdar, and C. Ersoy, “Wireless sensor networks for healthcare: a survey,”, Computer Networks, 54(15), p2688-2710, (2010).
[https://doi.org/10.1016/j.comnet.2010.05.003]

-
M. Caporuscio, P. G. Raverdy, and V. Issarny, “UbiSOAP : A service-oriented middleware for ubiquitous networking,”, IEEE Transactions on Services Computing, 5(1), p86-98, (2012).
[https://doi.org/10.1109/TSC.2010.60]

- T. H. Kim, N. J. Bae, M. B. Lee, C. S. Shin, J. W. Park, and Y. Y. Cho, “A study of an agricultural ontology model for an intelligent service in a vertical farm,”, Journal of International Smart Home, 7(4), p118-126, (2013).
-
D. Perez-Diaz de Cerio, S. R. Boque, J. Rosell-Ferrer, J. Ramos-Castro, J. L. Valenzuela, and J. M. Colome, “The help4mood wearable sensor network for inconspicuous activity measurement,”, IEEE Wireless Communications, 20(4), p50-56, (2013).
[https://doi.org/10.1109/MWC.2013.6590050]

-
E. L. van den Broek, “Ubiquitous emotion-aware computing,”, Personal and Ubiquitous Computing, 17(1), p53-67, (2013).
[https://doi.org/10.1007/s00779-011-0479-9]

-
S. Woo, S. Jeong, E. Mok, L. Xia, C. Choi, M. Pyeon, and J. Heo, “Application of WiFi-based indoor positioning system for labor tracking at construction sites: A case study in Guangzhou MTR”, Automation in Construction, 20(1), p3-13, (2011).
[https://doi.org/10.1016/j.autcon.2010.07.009]

-
P. Mirowski, P. Whiting, H. Steck, R. Palaniappan, M. MacDonald, D. Hartmann, and T. K. Ho, “Probability kernel regression for WiFi localisation,”, Journal of Location Based Services, 6(2), p81-100, (2012).
[https://doi.org/10.1080/17489725.2012.694723]

-
L. Chen, B. Li, K. Zhao, C. Rizos, and Z. Zheng, “ An improved algorithm to generate a Wi-Fi fingerprint database for indoor positioning,”, Sensors, 13(8), p11085-11096, (2013).
[https://doi.org/10.3390/s130811085]

- http://www.ZigBee.org/en/about/faq.asp, Accessed June 17, 2013.
-
J. V. Marti, J. Sales, R. Marin, and E. Jimenez-Ruiz, “Localization of mobile sensors and actuators for intervention in low-visibility conditions: The zigbee fingerprint approach,”, Journal of International Distributed Sensor Networks, 2012, article ID 951213, p1-10, (2012).
[https://doi.org/10.1155/2012/951213]

-
C. H. Oh, “Location estimation using space time signal processing in RFID wireless sensor networks,”, Journal of International Distributed Sensor Networks, 2013, article ID 634531, p8, (2013).
[https://doi.org/10.1155/2013/634531]

-
G. Garcia, L. Muppirisetty, and H. Wymeersch, “On the trade-off between accuracy and delay in UWB navigation,”, IEEE Communications Letters, 17(1), p39-42, (2013).
[https://doi.org/10.1109/LCOMM.2012.120312.121542]

-
H. Jiang, C. Liu, Y. Zhang, and H. Cui, “Fast 3D node localization in multipath for UWB wireless sensor networks using modified propagator method,”, Journal of International Distributed Sensor Networks, 2014, article ID 312535, p8, (2014).
[https://doi.org/10.1155/2014/312535]

-
A. D. Angelis, S. Dwivedi, and P. handel, “Characterization of a flexible UWB sensor for indoor localization,”, IEEE Transactions on Instrumentation and Measurement, 62(5), p905-913, (2013).
[https://doi.org/10.1109/TIM.2013.2243501]

-
S. Lee, H. Shin, R. Ha, and H. Cha, “IEEE 802.15.4a CSS-based mobile object locating system using sequential Monte Carlo method,”, Computer Communications, 38(1), p13-25, (2014).
[https://doi.org/10.1016/j.comcom.2013.10.008]

-
J. Wang, Q. Gao, Y. Yu, H. Wang, and M. Jin, “Toward robust indoor localization based on Bayesian filter using chirp-spread-spectrum ranging,”, IEEE Transactions on Industrial Electronics, 59(3), p1622-1629, (2012).
[https://doi.org/10.1109/TIE.2011.2165462]

-
M. P. Michaelides, and C. G. Panayiotou, “SNAP: fault tolerant event location estimation in sensor networks using binary data,”, IEEE Transactions on Computers, 58(9), p1185-1197, (2009).
[https://doi.org/10.1109/TC.2009.60]

-
X. Liu, and X. Ma, “Target localization and tracking in noisy binary sensor networks with known spatial topology,”, Wireless Communications and Mobile Computing, 9(8), p1028-1039, (2009).
[https://doi.org/10.1002/wcm.652]

-
E. Masazade, R. Niu, P. K. Varshney, and M. Keskinoz, “Energy aware iterative source localization for wireless sensor networks,”, IEEE Transactions on Signal Processing, 58(9), p4824-4835, (2010).
[https://doi.org/10.1109/TSP.2010.2051433]

-
W. Meng, W. Xiao, and L. Xie, “An efficient EM algorithm for energy-based multisource localization in wireless sensor networks,”, IEEE Transactions on Instrumentation and Measurement, 60(3), p1017-1027, (2011).
[https://doi.org/10.1109/TIM.2010.2047035]

-
L. Cheng, C. D. Wu, Y. Z. Zhang, and Y. Wang, “Indoor robot localization based on wireless sensor networks,”, IEEE Transactions on Consumer Electronics, 57(3), p1099-1104, (2011).
[https://doi.org/10.1109/TCE.2011.6018861]

-
S. W. Lee, D. Y. Lee, and C. W. Lee, “Enhanced DV-Hop algorithm with reduced hop-size error in ad hoc networks,”, IEICE Transactions on Communications, 94(7), p2130-2132, (2011).
[https://doi.org/10.1587/transcom.E94.B.2130]

-
J. Lee, W. Chung, and E. Kim, “A new range-free localization method using quadratic programming,”, Computer Communications, 34(8), p998-1010, (2011).
[https://doi.org/10.1016/j.comcom.2010.10.013]

-
Z. Zhong, and T. He, “RSD: a metric for achieving rangefree localization beyond connectivity,”, IEEE Transactions on Parallel and Distributed Systems, 22(11), p1943-1951, (2011).
[https://doi.org/10.1109/TPDS.2011.105]

-
K. Lu, X. Xiang, D. Zhang, R. Mao, and Y. Feng, “Localization algorithm based on maximum a posteriori in wireless sensor networks,”, International Journal of Distributed Sensor Networks, 2012, article ID 260302, p7, (2012).
[https://doi.org/10.1155/2012/260302]

-
L. Cheng, C. Wu, Y. Zhang, H. Wu, M. Li, and C. Maple, “A survey of localization in wireless sensor network,”, Journal of International Distributed Sensor Networks, 2012, Article ID 962523, p12, (2012).
[https://doi.org/10.1155/2012/962523]

-
Y. Kim, Y. Chon, and H. Cha, “Smartphone-based collaborative and autonomous radio fingerprinting,”, IEEE Transactions on System, Man, and Cybernetics, Part C: Applications and Reviews, 42(1), p112-122, (2012).
[https://doi.org/10.1109/TSMCC.2010.2093516]

-
M. Lee, and D. han, “Voronoi tessellation based interpolation method for Wi-Fi radio map construction,”, IEEE Communications Letters, 16(3), p404-407, (2012).
[https://doi.org/10.1109/LCOMM.2012.020212.111992]

-
S. J. Halder, T. Y. Choi, J. H. Parks, S. H. Kang, S. W. Park, and J. G. Park, “Enhanced ranging using adaptive filter of ZIGBEE RSSI and LQI measurement,”, Proceedings of the 10th International Conference on Information Integration and Web-Based Applications Services, p367-373, (2008).
[https://doi.org/10.1145/1497308.1497374]

- S. J. Halder, and W. Kim, “A fusion approach of RSSI and LQI for indoor localization system using adaptive smoothers,”, Journal of Computer Networks and Communication, 2012, article ID 790374, p1-10, (2012).
- Texas Instruments, http://www.ti.com/lit/ds/symlink/cc2420.pdf, Accessed February, 10, 2014.