고속영역에서 전류형상에 따른 스위치드 릴럭턴스 발전기의 효율 개선

1. 서 론

스위치드 릴럭턴스 발전기(이하 SRG라고 한다)는 구조상 많은 이점이 있다. 회전자는 단지 성층철심으로만 구성되어 매우 간단하며, 고정자는 돌극으로 되어 있는 자극에 집중권으로 구성되어 제작비용을 줄일 수 있으므로 상업적 측면에서 유리하다[1][2]. 또한 회전자에는 권선이나 영구자석이 없으므로 고속 운전 및 나쁜 주위 환경에서도 유리하다[3]. SRG의 각 상은 전기적으로나 자기적으로 다른 상과 독립적이어서 시스템 신뢰성이 높다[4][5].

현재까지 SRG의 시스템 효율을 개선하는 것에 관해 다양한 문헌들이 보고되고 있다. 전체 운전 속도 범위에 대하여 원하는 역률을 얻기 위해 스위칭 각 설정에 관한 연구[6], 상과 상사이의 전류 과정에 프리휠링 단계를 추가하여 발전기 출력을 향상시키는 방법[7] 및 시스템 효율과 토크 리플 해석에 근거하거나[8] 고정자와 회전자가 겹치기 시작하는 위치에서 자속과 최대 자속의 비로 턴온/턴오프 각의 선정에 관한 연구[9]가 있다.

문헌[10]은 여러 가지 기준 출력과 속도에서 시스템의 손실에 관한 측정과 해석을 통하여 높은 시스템 효율에 해당하는 스위칭 각도를 설정한다. 또한 측정한 자화곡선을 근거로 다양한 턴온/턴오프 각도에 대한 출력과 시스템 효율 해석을 근거로 턴온/오프 각도를 설정하는 방법도 제시되고 있다[11].

SRG는 구조상 내환경성이 우수하여 풍력이나 소수력 발전과 같이 운전속도 범위가 넓은 경우에 쉽게 적용될 수 있다. 이러한 구동원은 속도 변동 범위가 넓기 때문에 정격속도 이상의 범위에서도 효율 개선이 요구된다.

본 논문에서는 정격속도 이상의 범위에 대해서도 발전기에 흐르는 상전류 형상을 조정하여 SRG 시스템의 효율을 개선하는 것이다. 정격속도 및 정격속도 이상의 범위에 걸쳐 효율 개선을 위한 스위칭각 영향을 검토하고, 시뮬레이션과 실험 결과로 검증한다.

2. SRG 동작 해석

2.1 SRG의 동작 원리

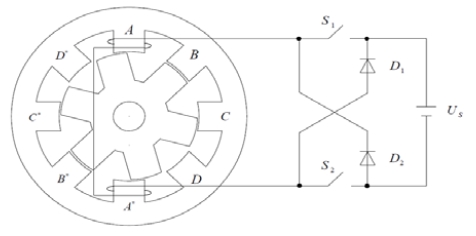
Figure 1은 SRG 구동 회로의 일부이다. SRG가 여자될 때, 한 상에 대한 전압 방정식은 다음과 같다.

Figure 1:

The schematic diagram of SRG

여기서 첨자 p는 상을 나타내며, R_p은 상의 저항, L은 상의 인덕턴스이며 회전자 위치와 상전류의 함수이다. 그리고 e_p는 역기전력이며, ω_r은 발전기 회전속도이다.

Equation (1)에서 상전류는 역기전력과 전원 전압에 의존한다. 역기전력의 크기는 회전자 속도에 따라 변하므로 결과적으로 전류 모양은 전동기 속도에 따라 변한다.

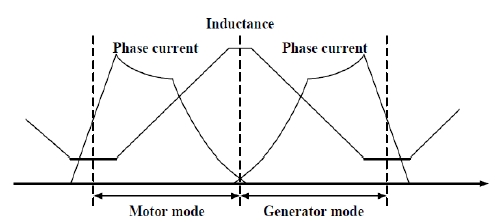
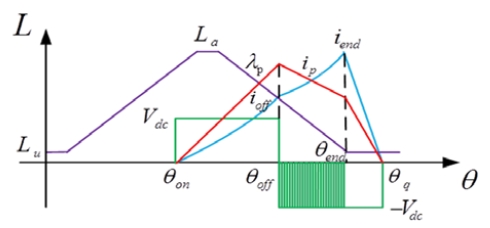
Figure 2는 전동기 동작과 발전기 동작에 대한 인덕턴스 형상과 상전류의 관계를 보여주고 있다.

$\[ \begin{array}{c}{U}_s=R_p{i}_p+L(i_p, \theta )\frac{d{i}_p}{dt}+e_p\hfill \\ e_p=\frac{\partial L(i_p,\theta )}{\partial \theta }{\omega }_r{i}_p\hfill \end{array} \]$

(1)

Figure 2:

Relationship between motor and generator operation of the switched reluctance machine

2.2 주요 전기 손실 계산

SRG의 주요 전기 손실은 동손과 철손이다. 동손은 전류 형상으로부터 구할 수 있고, 다음 식으로 주어진다.

$\[ {\displaystyle P_{cu}=m{I}_{rms}^2{R}_p} \]$

(2)

$\[ {\displaystyle I_{rms}=\sqrt[]{\frac{1}{{\theta }_{rp}}{\int }_{{\theta }_{rp}}^{{\theta }_q}{i}_{pg}^{2}d\theta }} \]$

(3)

여기서 m은 상 수, I_rms는 상전류의 실효값이며, θ_rp는 회전자 극피치, N_r은 회전자 자극 수이다. θ_on과 θ_q는 턴온 각과 상전류가 영이 될 때 회전자 위치이다.

철손은 히스테리시스손과 와류손의 합이며, 이들은 최대 자속밀도와 자계의 교번 주파수와 관련된다. 자속 밀도는 정현적이 아니며, 자기 회로 지점에 따라 다르기 때문에, 철손은 코어내부에서 균일하게 분포되지 않는다. 본 논문에서는 철손은 SRG 각 부분의 실제 자속 밀도를 바탕으로 근사화된 식으로 계산한다. 푸리에 급수를 이용하여 자속밀도의 기본파 성분과 고조파 성분의 크기를 계산한다. 코어의 단위 무게 당 손실을 계산하기 위한 근사 방정식은 다음 Equation (4)와 같다.

$\[ {\displaystyle P_{fe}=K_{h}f{B}_m^2+K_c{\left(f{B}_m\right)}^2} \]$

(4)

여기서 f는 주파수, K_h와 K_c는 각각 히스테리시스손 및 와류손 계수이며, B_m은 최대 자속밀도이다. 자기회로 각 부분의 기본 주파수는 Equation (5) - (8)로 계산된다[12].

$\[ {\displaystyle f_{SP}={\omega }_r{N}_r/2\pi } \]$

(5)

$\[ {\displaystyle f_{RP}=f_{SP}/N_r} \]$

(6)

$\[ {\displaystyle f_{SY}=k\times f_{SP} 1\le k \le m} \]$

(7)

$\[ {\displaystyle f_{RP}=f_{SP}/N_r} \]$

(8)

여기서 f_SP, f_RP, f_SY 및 f_RY는 각각 고정자 자극, 회전자 자극, 고정자 요크 및 회전자 요크의 기본 주파수이다.

Figure 3:

Flux paths in switched reluctance machine

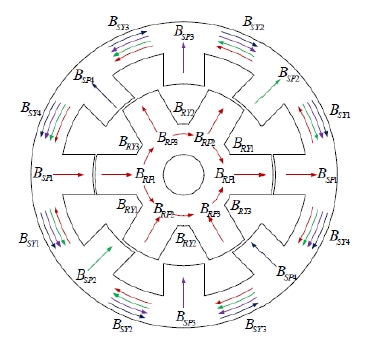
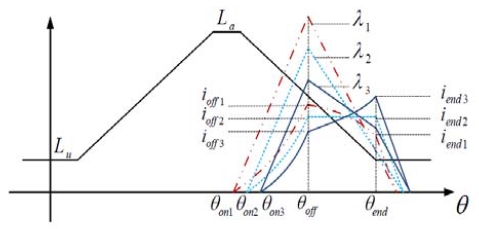
Figure 3은 발전기 각 부분에 대한 자속흐름을 나타내는 단면도이다. 고정자 자극의 자속밀도로부터 다른 부분의 자속밀도를 계산할 수 있으며, 각각의 자속밀도는 다음 Eqaution (9) - (12)로 계산된다[12].

$\[ {\displaystyle B_{SP1}=L\times i_{ph}/2\times N\times A_{SP}} \]$

(9)

$\[ {\displaystyle B_{SP1}=\frac{A_{SP}}{A_{RP}}{B}_{SP1}} \]$

(10)

$\[ {\displaystyle B_{SY}=\left[\begin{array}{c}{B}_{SY1}\\ B_{SY2}\\ B_{SY3}\\ B_{SY4}\end{array}\right]=\frac{A_{SP}}{2A_{SY}}{B}_{SP}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]} \]$

(11)

$\[ {\displaystyle B_{RY}=\left[\begin{array}{c}{B}_{RY1}\\ B_{RY2}\\ B_{RY3}\end{array}\right]=\frac{A_{RP}}{2A_{RY}}{B}_{RP}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]} \]$

(12)

단,

$\[ \begin{array}{c}{B}_{SP}=\left[\begin{array}{cccc}{B}_{SP1}& -B_{SP2}& -B_{SP3}& -B_{SP4}\\ B_{SP1}& B_{SP2}& -B_{SP3}& -B_{SP4}\\ B_{SP1}& B_{SP2}& B_{SP3}& -B_{SP4}\\ B_{SP1}& B_{SP2}& B_{SP3}& B_{SP4}\end{array}\right]\hfill \\ B_{RP}=\left[\begin{array}{ccc}{B}_{RP1}& -B_{RP2}& -B_{RP3}\\ B_{RP1}& B_{RP2}& -B_{RP3}\\ B_{RP1}& B_{RP2}& B_{RP3}\end{array}\right]\hfill \end{array} \]$

여기서, N은 고정자 자극당 권수, A_SP, A_SY, A_RP 및 A_RY는 각각 고정자 자극, 고정자 요크, 회전자 자극 및 회전자 요크의 면적이다.

단위 중량 당 철손은 고조파 성분의 합으로 구하며, 발전기 전체 철손은 각 부분의 철손의 합이다.

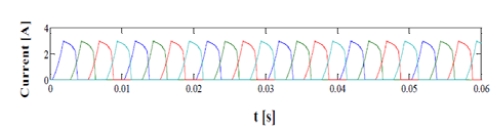
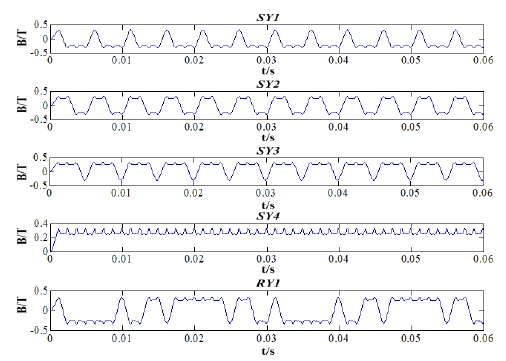
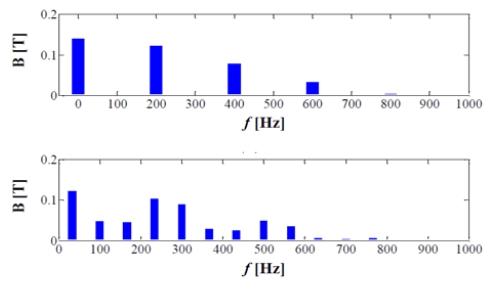
Figure 4는 SRG에서 자속밀도 계산에 적용할 상전류 모양이며, Figure 5는 고정자와 회전자 요크에서 자속밀도를 나타내고, Figure 6은 고정자 자극과 회전자 자극의 자속밀도에 대한 FFT 결과이다.

Figure 4:

Actual phase current waveform

Figure 5:

Flux densities in the various parts of the stator and rotor yoke

Figure 6:

FFT analysis of the stator and rotor pole flux densities

2.3 SRG의 효율

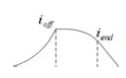
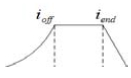
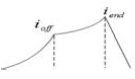
SRG에는 3가지 형태의 전류 파형이 있다. 전류 변화의 방향 표시를 편리하게 하도록 전류변화율(Current Slope Factor, CSF)을 사용한다. 전류변화율과 전류 모양과의 관계는 Table 1에 나타낸다[12][13].

Table 1:

Relationship between CSF notation and current shape

Table 1에서 i_off와 i_end는 θ_off와 θ_end에서 전류 크기이며, θ_off는 턴오프 각도이며, θ_end는 고정자 자극과 회전자 자극의 중첩이 끝나는 회전자 위치이다.

1) 정격속도 이하에서 운전

SRG가 임의의 일정출력에 저속으로 운전되는 경우를 고려한다. 적절한 스위칭 각 설정에 따라 3가지 형태의 CSF를 갖는 전류를 얻을 수 있다.

Figure 7은 동일한 출력 조건에서 3가지 전류 및 이에 해당하는 자속쇄교수를 나타낸다.[13]

Figure 7:

Phase current and flux linkage of various current shapes at the same output power

Equation (1)과 Figure 7을 참고하면, CSF가 ‘+’일 때 상전압의 크기는 가장 낮고, 그 결과 전류의 실효값은 가장 크게 된다. 바꾸어 말하면 동일한 출력에서 CSF가 ‘+’ 일 때 동손이 증가한다는 의미이다.

자속 쇄교수는 θ_off 일 때 최대가 되며, 철손은 동일한 출력조건에서 CSF가 ‘+’일 때 감소한다.

그러므로 동손과 철손의 합인 전체 손실이 가장 적게 되는 CSF가 존재하며, SRG가 저속으로 운전할 동안에는 적정 CFS값에 의해 효율이 개선될 수 있다.

2) 정격속도 이상에서 운전

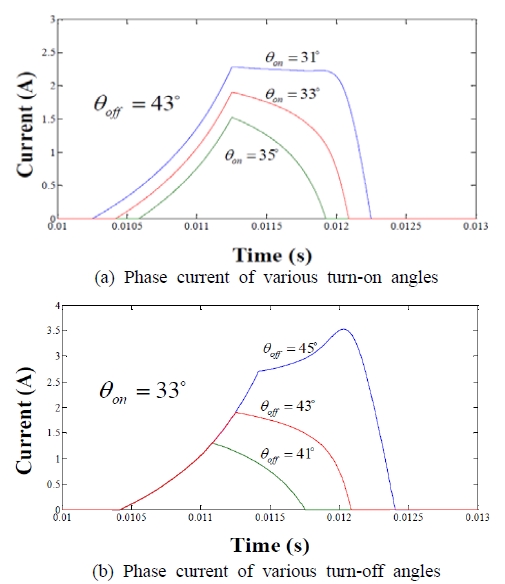
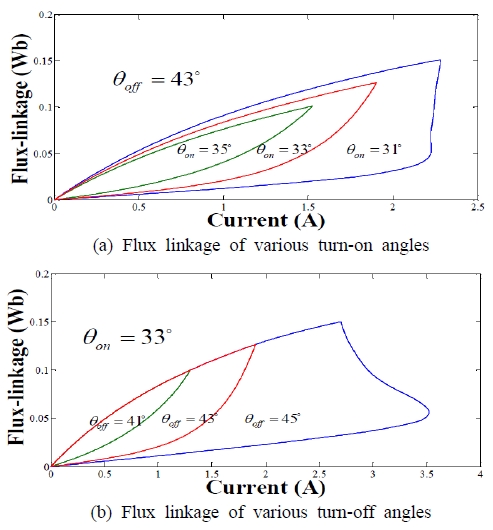
SRG가 정격속도 이상의 고속 운전일 경우에는 역기전력이 전원전압보다 높기 때문에 정격운전 경우처럼 스위치 동작에 의한 전류형상 제어는 곤란하다. 그러므로 SRG 효율을 개선하기 위해서는턴온과 턴오프 각도가 유일한 제어 변수이며, Figure 8과 Figure 9는 턴온/오프 각의 변화에 따른 상전류와 쇄교자속의 변화를 나타낸 것이다.

Figure 8(a)는 턴오프 각도를 일정하게 두고, 턴온각도를 각각 31°, 33° 및 35°로 설정할 경우의 전류이며, Figure 8(b)는 턴온 각도를 33°로 설정하고 턴오프 각도를 41°, 43° 및 45°로 변경한 경우의 전류형상이다.

Figure 8:

Influence of turn-on and turn-off angles on phase current shape

Figure 9:

Flux linkage of various turn-on and turn-off angles

Figure 8과 Figure 9로부터 전류는 턴오프각도에 대해 민감하므로 턴오프각도는 일정하게 두고 턴온각도를 조정하는 것이 전류형상을 효과적으로 제어할 수 있다.

3. SRG 구동 시스템

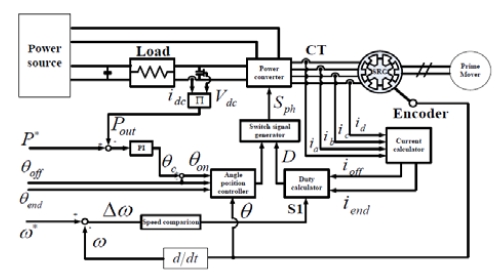
본 논문에서 사용된 시스템 구성을 Figure 10에 나타낸다. 시스템은 전원, SRG, 기계적 동력구동원, 전력변환기 및 각종 제어기들로 구성되어 있다. 기계적 구동원인 원동기로부터 SRG로 전달된 에너지는 부하 측으로 전기에너지를 공급한다. P*와 P_out은 전력 지령값과 출력이다. ω*와 ω 그리고 ∆ω는 SRG의 정격 각속도, 실제 각속도 및 속도오차이다.

Figure 10:

System structure for SRG

Figure 11은 전체 운전 영역에 대한 효율을 개선하기 위해 상전류 형상을 제어할 수 있도록 전류제어 기능을 갖는 스위칭각 제어 방법을 나타낸다.

Figure 11:

Switching angle control with current controller

정격속도 이하의 운전에서는 Figure 11에서처럼 원하는 CSF값을 얻기 위해 스위칭 각은 일정하게 하고, 턴오프 각도 이후에 직접 전류를 제어하는 방법을 적용한다.

정격속도 이상인 경우 전류 형상을 제어하기 위해서는 단지 스위칭 각의 조정에 의해서만 가능하다. Figure 8에서처럼 턴온 각도를 빠르게 하면 전류기울기 CSF는 ‘-’에서 ‘+’로 점차 이동하고, 턴오프 각도를 느리게 하여도 같은 모양으로 전류기울기가 변화한다. 정격속도 이상에서는 턴오프각도를 고정하고, 턴온각도를 조정하여 전류기울기를 제어한다.

4. 시뮬레이션 및 실험결과

Table 2는 시뮬레이션 및 실험에 사용된 발전기의 파라미터이다.

Table 2:

Specifications for parameters of SRG

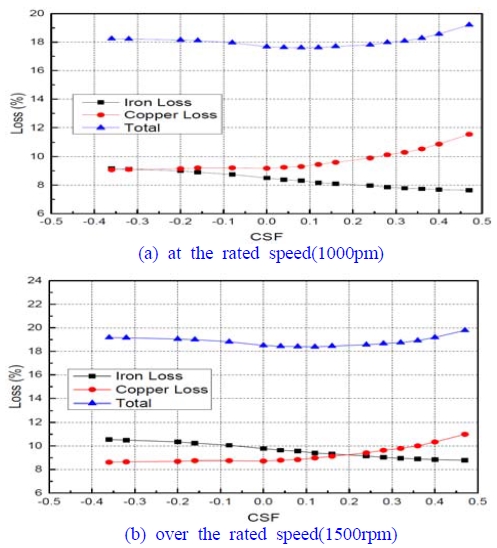
Figure 12는 SRG가 정격속도 및 정격속도 이상에서 운전될 경우 CSF와 손실관계를 나타낸 것이다. 전류기울기 CSF값은 다음 식으로 정하였다.

Figure 12:

Loss variation due to variable CSF

동손은 정격속도 이상에서 운전할 경우 정격속도와 비교할 때 거의 차이가 없으나, 철손은 정격속도 이상에서 전반적으로 약간 증가하는 경향을 보이며, 이것은 스위칭 주파수 증가에 기인하는 것으로 고려된다.

전류기울기, CSF가 증가함에 따라 동손은 증가하는 반면 철손은 감소하고, CSF가 영부근에서 전체 손실이 최소가 되는 것을 알 수 있다.

Figure 13:

Efficiency for output power in simulation

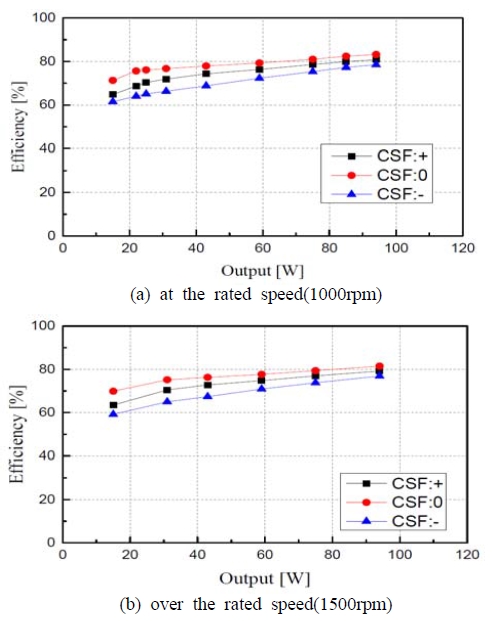
Figure 13은 CSF에 대한 효율을 시뮬레이션한 결과이다. 운전 조건은 직류링크전압 100[V], 정격속도 1000[rpm] 및 정격 이상속도 1500[rpm]이다. 정격속도에서 턴오프각은 42°이며, 정격이상의 속도에는 Figure 14의 결과로부터 턴오프각은 46°로 설정하였다. 효율은 단지 동손과 철손만 고려하고, Equation (14)로 계산한다.

Figure 14:

Relationship between efficiency and turn-off

Figure 13으로부터 2가지의 속도에 대하여 전류기울기 CSF가 0인 경우 전체적으로 높은 효율을 나타내고 있는 것을 알 수 있다.

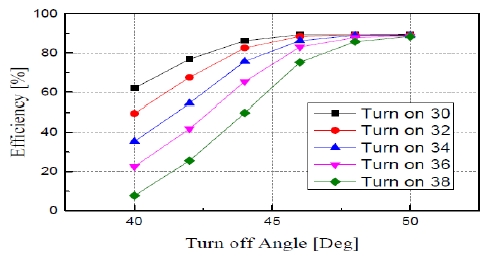
Figure 14는 고속운전에서 전류형상 조정은 스위칭각도 조정에 의해서만 가능하므로 몇 가지 턴오프 각도를 설정하고 턴온각 변화에 따른 효율을 검토한 결과이다. 턴오프각이 턴온각보다 전력변환에 크게 영향을 끼치므로 SRG가 정격속도 이상에서 고속 운전될 경우 턴오프각을 적정 값으로 설정하고, 턴온각도를 조정하는 것이 유리하다. Figure 14로부터 적정한 턴오프각은 실제 설정을 고려하여 46°를 선택하였다. 턴온각도의 변화에 대해 턴온각도가 작을수록 권선에 흐르는 전류값이 증가하기 때문에 발전 출력의 증가와 더불어 효율 증가를 나타내고 있다.

Figure 15는 본 실험에 사용된 실험장치이다. AC 서보전동기가 구동원으로 사용되고, DSP가 주요 제어를 담당하고 있다.

Figure 15:

Experimental setup

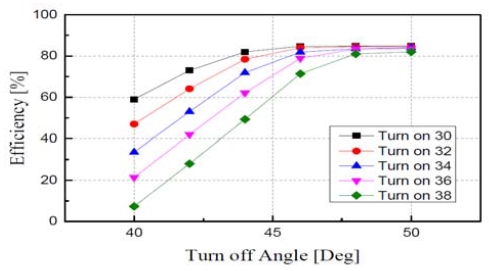
Figure 16은 정격속도 이상의 고속운전에서 적정한 전류형상을 조정하기 위해 특정 턴오프각도를 설정하고 턴온각의 변화에 따른 효율을 측정한 결과이다. 시뮬레이션과 비슷한 결과를 나타내고, 턴오프각도는 46°를 선정하고, 턴온각도의 조정으로 전류형상을 조정하였다. 턴온각 30°는 전류기울기가 ‘+’이며, 38°는 ‘-’에 해당한다.

Figure 16:

Relationship between efficiency and turn-off

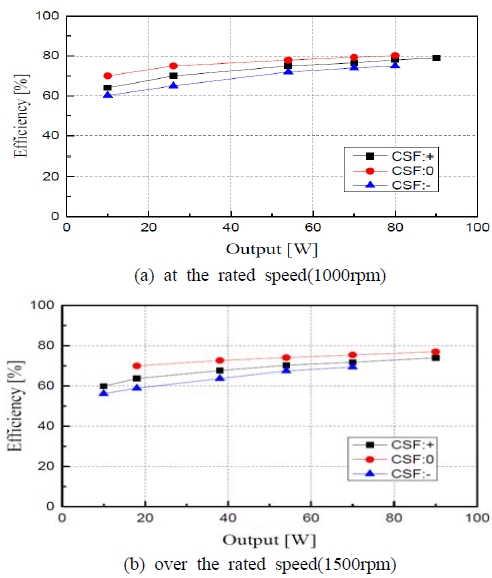
Figure 17은 CSF와 효율과의 관계를 측정한 실험 결과이다. 링크전압은 100[V], 운전속도는 정격속도와 정격속도의 150%인 1000[rpm]과 1500[rpm]이다. 정격속도에서 턴오프각은 42°이며, 정격속도 이상의 1500[rpm]에서는 46°이다. 그림으로부터 시스템의 효율은 CSF가 ‘0’일 경우 최대가 되는 것을 알 수 있다.

Figure 17:

Relationship between efficiency and CSF

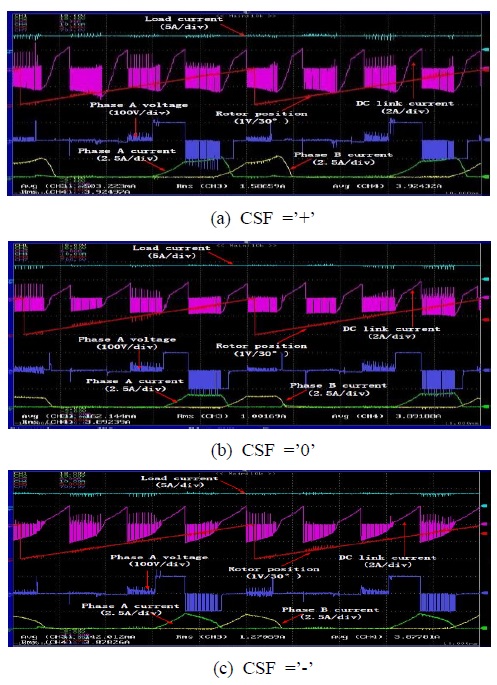
Figure 18은 SRG가 정격속도 1000[rpm]으로 운전될 경우 3가지 전류 형상에 대하여 측정한 결과이다.

Figure 18:

Experimental waveforms according to various current shapes

5. 결 론

풍력이나 소수력 발전의 경우 발전기는 정격속도 이상의 조건에서 운전될 수 있으며, 이러한 경우에 SRG의 시스템 효율도 검토가 요구된다. 본 논문에서는 정격속도 이상의 범위에 걸쳐 SRG의 효율을 개선하는 것에 대하여 기술하였다. 정격속도 이상의 범위에서도 전류 형상이 주요 전기적 손실에 미치는 영향이 해석되었고, 시스템 효율을 개선하기 위해 사용될 수 있는 제어방법이 제시되었다. 정격속도 이상의 범위에서는 턴오프각도를 일정하게 하고, 턴온각도를 조정하여 발전 출력 및 효율을 개선할 수 있음을 보였다. 시뮬레이션과 실험결과는 이론적인 해석을 검증하기 위해 행하여졌다. SRG 시스템 효율은 전체 속도 범위에 걸쳐 전류변화율이 ‘0’일 경우 효율이 높게 나타내었고, 발전량만을 고려할 경우에는 전류변화율이 ‘+’일 때 높다.

Acknowledgments

‘이 논문은 부경대학교 자율창의학술연구비(2014년)에 의하여 연구되었음’

References

• D. A. Torrey, “Switched reluctance generators and their control”, IEEE Transactions on Industrial Electronics, 49(1), p3-14, (2002). [https://doi.org/10.1109/41.982243]
• Y. Sozer, and D. A. Torrey, “Closed loop control of excitation parameters for high speed switched reluctance generators”, IEEE Transactions on Power Electronics, 19(2), p355-362, (2004). [https://doi.org/10.1109/TPEL.2003.823178]
• D. E. Cameron, and J. H. Lang, “The control of high speed variable-reluctance generators in electric power systems”, IEEE Transactions on Industry Applications, 29(6), p1106-1109, (1993). [https://doi.org/10.1109/28.259720]
• A. Radun, “Generating with the switched reluctance motor”, Proceedings of the 9th IEEE Applied Power Electronics Conference and Exposition (APEC’94), 1, p41-47, (1994). [https://doi.org/10.1109/APEC.1994.316421]
• V. Nedic, and T. A. Lipo, “Experimental verification of induced voltage self-excitation of a switched reluctance generator”, Proceedings of the 35th IEEE Industry Applications Society Annual Meeting (IAS’00), 1, p51-56, (2000). [https://doi.org/10.1109/IAS.2000.880981]
• E. Mese, Y. Sozer, J. M. Kokernak, and D. A. Torrey, “Optimal excitation of a high speed switched reluctance generator”, Proceedings of the 15th IEEE Applied Power Electronics Conference and Exposition (APEC’00), 1, p362-368, (2000). [https://doi.org/10.1109/APEC.2000.826128]
• B. Fahimi, and S. Dixon, “Enhancement of output electric power in switched reluctance generators”, Proceedings of the IEEE Electric Machines and Drives Conference (IEMDC’03), 2, p849-856, (2003).
• C. Mademlis, and I. Kioskeridis, “Optimizing performance in current-controlled switched reluctance generators”, IEEE Transactions on Energy Conversion, 20(3), p556-565, (2005). [https://doi.org/10.1109/TEC.2005.852960]
• I. Kioskeridis, and C. Mademlis, “Optimal efficiency control of switched reluctance generators”, IEEE Transaction on Power Electronics, 21(4), p1062-1072, (2006). [https://doi.org/10.1109/TPEL.2006.876827]
• Z. Li, D. Gao, and J. W. Ahn, “Power closed-loop control of switched reluctance generator for high efficiency operation”, Journal of International Conference on Electrical Machines and Systems, 1(3), p128-133, (2012). [https://doi.org/10.11142/jicems.2012.1.3.397]
• J. Faiz, and R. Fazai, “Optimal excitation angles of a high speed switched reluctance generator by efficiency maximization”, Proceedings of the 12th Power Electronics and Motion Control Conference (EPE-PEMC’06), p287-291, (2006). [https://doi.org/10.1109/EPEPEMC.2006.4778414]
• Z. Li, S. Yu, and J. W. Ahn, “High-efficiency operation of switched reluctance generator based on current waveform control”, Journal of International Conference on Electrical Machines and Systems, 2(1), p120-126, (2013). [https://doi.org/10.11142/jicems.2013.2.1.120]
• S. Yu, D. H. Lee, and J. W. Ahn, “Efficiency analysis of switched reluctance generator according to current shape under rated speed”, Journal of International Conference on Electrical Machines and Systems, 2(4), p491-497, (2013). [https://doi.org/10.11142/jicems.2013.2.4.491]