선박 조종운동을 위한 통합제어시스템에서의 이동운동제어에 관한 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
일반적으로 선박의 운동은 이동운동과 회전운동의 결합으로 이루어진다. 특히 대형 크루즈 선박과 광케이블 포설용 선박, 다이버용 선박 등 특수 선박은 자동 접이안이나 설정된 경로 등을 따라 선수방향의 변화 없이 여러 방향으로 이동만 하는 운동을 재현할 수 있어야 한다. 본 논문에서는 다 추력장치를 가진 선박을 대상으로 조이스틱 명령 기반의 이동운동제어를 실현할 수 있는 통합제어시스템의 구성방법을 제안하며, 이를 실현하기 위하여 필요한 속도명령 생성방법과 대응하는 운동변수 및 이들이 가져야 하는 기준 값 생성방법을 제안한다. 또한 정의된 운동변수의 기준 값을 추종하기 위한 다양한 알고리즘 구성에 대하여 논한다. 또한 통합제어시스템 시뮬레이션 프로그램을 작성하고 이를 토대로 다양한 이동운동 명령에 대한 모의실험을 수행한 후, 시뮬레이션 결과를 바탕으로 제안된 방법의 유효성을 검증한다.
Abstract
In general, a series of ship steering motion is represented by the combination of translational motion and rotational motion of the ship. Especially, special-functioned ships such as large-scale cruises, ships for installing underwater optical cable, and diver ships must be able to reveal only a translational motion without the change of orientation. In this paper, a method to comprise an integrated control system based on the joystick as a command instrument for translational motion control is suggested. In order to realize the translational motion control system, several algorithms are suggested including the velocity command generation, the selection of motional variables, and the generation and tracking of reference inputs for the selected motional variables. A simulation bench is composed to execute simulations for several translational motion commands. At last, the effectiveness of the proposed method is verified by analyzing the simulation results.
Keywords:
Ship steering motion, Integrated control system, Translational motion, Velocity command, Motional variables키워드:
선박 조종운동, 통합제어시스템, 이동운동, 속도명령, 운동변수1. 서 론
선박 운항의 주요한 목적은 항해 중 발생할 수 있는 좌초, 침몰, 충돌로부터 선박의 안전성을 확보하는 문제와 정해진 항로를 정확하게 추종하는 문제로 요약할 수 있다. 최근에는 특수선을 대상으로 한 회두각 유지 및 변침을 지향하는 기본 오토 파이럿 제어를 비롯하여, 해도를 이용한 설정된 항로의 추종제어, 자동 접이안 제어, 조류나 바람 등 외란의 영향에도 설정된 위치를 동적으로 유지하는 제어(Dynamic positioning control) 등과 같은 다양한 제어기능을 갖는 시스템에 관한 연구가 진행되어 왔다[1]-[4]. 최근 해상교통이 복잡해지고 선박이 대형화, 고속화됨에 따라 선박항해의 안정성 문제가 더 없이 중요한 이슈로 대두됨으로써 선박의 추진성능 향상뿐만 아니라 고도의 선박의 조종능력을 보유하기 위한 기술이 개발되고 있다. 특히 대형선박이 좁은 항구에서 출입항 할 때와 적하작업을 위하여 안벽으로 접이안 할 때에는, 선박에 설치된 다 추력장치(Multi-actuator)를 이용하여 능동적인 조종운동을 갖도록 함으로써 선박 스스로 운항안정성을 담보하도록 하는 노력이 진행되고 있다[5]-[9].
한편, 해저 광케이블 포설선이나 해저탐사선, 다이버용 선박, 낚시용 레저선박, 크루즈 여객선 등은 그 목적에 따라 다양한 선박운동을 필요로 한다. 이를 위해서는 오퍼레이터에 의해 명령되는 특수한 조종입력 장치와 다양한 형태의 추력장치를 선박에 설치하여야 하며, 이들을 통합하여 선박이 원하는 운동을 갖도록 제어해야 하는 선박운동 통합제어시스템 구성이 필요하다[10]-[13]. 그러나 이에 대한 선진화된 연구는 외국 선진업체들 중심으로 이루어지고 있으며 거의 공개되고 있지 않은 실정이다.
따라서 일반적인 대양 항해처럼 고속운동이 아닌 다양한 저속 조종운동을 대상으로 새로운 개념의 선박 통합제어시스템에 대한 전체적인 개념을 정립하는 것이 필요하고, 조종명령의 입력에서부터 선박운동의 재현까지 요구되는 구체적 모듈 개발에 대한 연구를 수행하는 것이 필요하다.
본 논문에서는 선박의 이동명령을 충분히 재현할 수 있는 다 추력장치를 가진 선박을 대상으로 조이스틱 기반의 이동운동 명령을 수행할 수 있는 통합제어시스템의 구성방법을 제안한다. 통합제어시스템을 구성하는데 필요한 구성요소로서 조이스틱 명령에 따른 다양한 속도명령 생성방법을 제안하고, 이를 추종하기 위하여 필요한 운동변수와 이들이 가져야 하는 기준 값 생성방법을 제안한다. 또한 정의된 운동변수의 기준 값을 추종하기 위해서 필요한 제어 알고리즘들을 제안한다. 또한 제안하는 이동운동 통합제어시스템의 성능을 검증하기 위하여 매트랩(MATLAB) 기반의 통합제어시스템 시뮬레이션 프로그램을 작성하고 이를 토대로 여러 가지의 이동운동 명령에 대한 모의실험을 수행한다. 마지막으로 시뮬레이션으로부터 얻은 결과를 분석함으로써 본 논문에서 제안하는 방법의 유효성을 검증한다.
2. 통합제어시스템 구성방법
본 논문에서 제안하는 이동운동을 위한 선박 통합제어시스템의 구성개념을 나타내면 Figure 1과 같다.
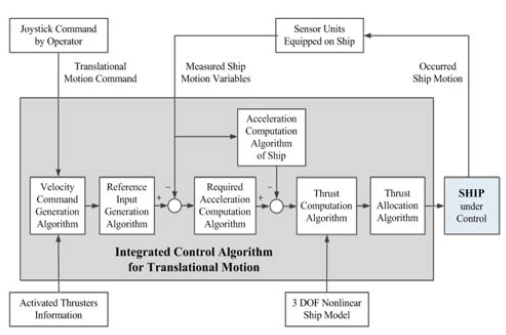
Functional diagram of an integrated control system for translational motion of ship based on joystick command
현재 선박에서 선박의 원하는 이동운동을 갖도록 하기 위하여 선박의 해당 축 방향에 대한 추력과 모멘트를 계산한 다음, 이들을 설치된 다 추력장치에 적절하게 할당함으로써 각 축 방향에서 발생된 선박운동이 원하는 운동이 될 때까지 발생된 선박의 운동정보를 피드백 하여 제어하는 구성방법이다.
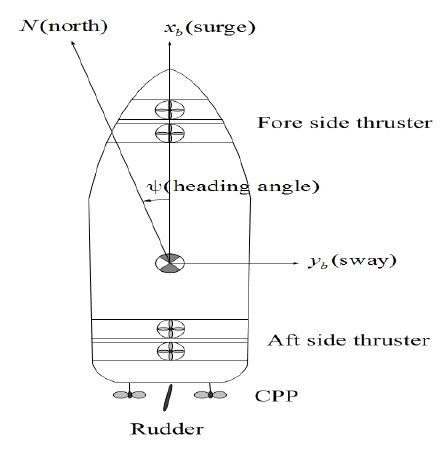
따라서 이동운동을 위한 통합제어시스템을 위하여 본 논문에서 대상으로 하는 선박모델은 Figure 2와 같이, 선체고정좌표계 기준으로 xb축(surge) 선수방향 및 yb축(sway) 횡 방향에 대한 이동운동과 zb축(heave)에 대한 회전운동 등 3자유도 조종운동을 제약조건 없이 충분히 발휘할 수 있도록, 추진을 위한 CPP (controllable pitch propeller) 2대가 좌우 대칭으로 선미에 설치되어 있고 선수와 선미 측에 각각 2대의 사이드 쓰러스터(side thruster)가 설치된 다 추력장치를 가진 선박이라고 가정한다.
Figure 1에서 제안하는 선박 통합제어시스템을 구성하기 위해서는 그림에서 보는 바와 같이 다음과 같은 알고리즘들이 구성되어야 한다. 첫째, 오퍼레이터의 조이스틱 조작에 의해 내려진 명령의 형태 즉 모드를 인식하고 그 명령에 대응하는 속도명령을 생성할 수 있는 알고리즘이 필요하다. 둘째, 인식된 명령을 토대로 선박운동을 재현하는데 필요한 선박운동 변수를 정의한 다음 기준 값을 계산하는 알고리즘이 필요하다. 셋째, 선박운동 변수의 기준 값과 현재 선박의 운동변수를 비교함으로써 운동 축별로 요구되는 추력과 추력모멘트를 계산하는데 필요한 선가속도와 각가속도를 계산하는 알고리즘이 필요하다. 넷째, 현재 발생된 선박운동변수와 계산된 선가속도와 각가속도를 이용하여 선박의 비선형 운동방정식으로부터 각 축별로 요구되는 추력과 추력모멘트를 계산하는 알고리즘이 필요하다. 다섯째, 선박 운동 축별로 계산된 추력과 추력모멘트를 선박에 설치된 다 추력장치에 적절히 할당하는 추력할당알고리즘이 필요하다. 3절에서는 통합제어시스템 구성에 필요한 모든 알고리즘에 대하여 상세히 기술한다.
3. 통합제어시스템 실현 알고리즘 개발
3.1 조이스틱 이동명령 인식과정
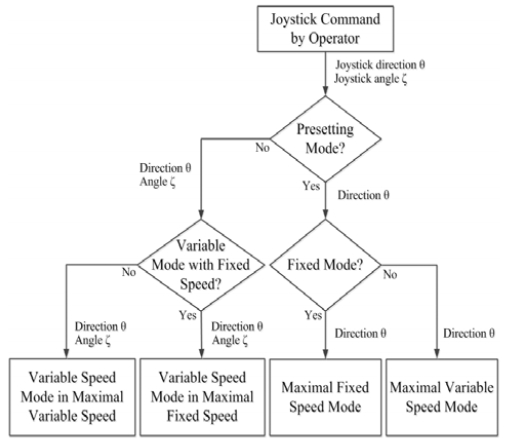
조이스틱을 이용하여 오퍼레이터에 의해 내려지는 이동운동에 대한 명령은 크게 설정속도 모드와 가변속도 모드로 정의할 수 있다. 설정속도 모드는 이동속도의 크기가 조이스틱의 경사각 ζ에는 관계없이 조이스틱의 방향각 에만 종속되어 그 방향으로 미리 설정된 최대의 속도를 갖도록 하는 명령의 형태이다. 이와 같은 설정속도 모드는 다시 최대 고정속도 모드와 최대 가변속도 모드로 구분할 수 있다. 가변속도 모드는 설정속도 모드 내에서 이동명령에 대한 속도의 크기가 조이스틱 경사각 ζ의 함수로 가변되도록 정의하는 모드이다. Figure 3은 조이스틱 명령으로 주어지는 조이스틱 방향각 θ와 경사각 ζ의 정보를 바탕으로 이동명령 모드를 인식하고 인식된 모드에 대응하는 변수 및 기준 값 생성 알고리즘으로 이동하는 과정을 나타낸 흐름도이다.
3.2 속도명령 모드의 정의와 속도명령 생성방법
선박의 조종운동에 있어서 선체의 구조와 사이드 쓰러스터의 추력용량 등을 고려할 때 횡 방향에서의 최대 이동속도를 전진방향의 속도에 대비하여 상대적으로 크게 하는 것은 불가능하다. 또한 선박의 안정조종 측면에서도 조종운동에서의 이동속도를 크게 할 필요가 없다. 이와 같은 관점에서 조종운동에서는 선박의 최대속도 크기를 제한하여 사용하는 것이 보편적이고 할 수 있다.
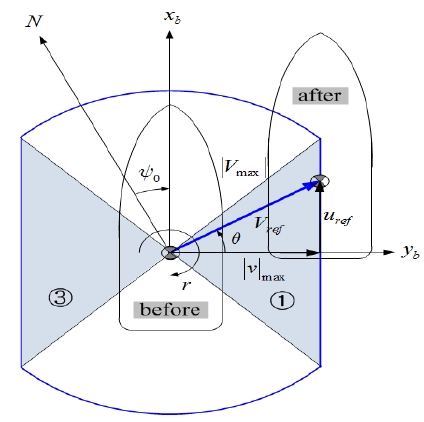
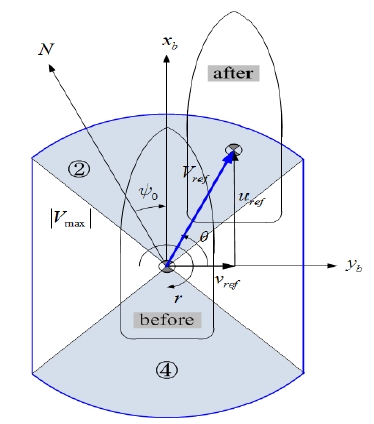
이동속도를 설정하는 모드 중에서 최대 고정속도 모드는, 사이드 쓰러스터의 정격용량을 고려하여 횡 방향으로 이동 가능한 최대속도의 크기를 고정시키고, 오퍼레이터에 의해 조작된 조이스틱의 모든 방향각 θ에 대하여 이동하도록 명령하는 모드로 정의된다. Figure 4는 최대 고정속도 모드를 정의하는 그림으로서, 선수방향에서의 속도변화 없이 조이스틱 방향각 θ로 이동하는데 필요한 속도의 크기가 횡 방향 최대속도의 크기 | Vref | = |ν|max로 자동 설정됨을 보여 준다. 또한 최대 고정속도 모드로 이동명령을 수행하는데 필요한 운동변수들 즉, 조이스틱 방향각 θ의 변화에 따른 xb축 즉 전진방향의 속도성분 uref, yb축 즉 횡 방향 속도성분 νref및 진북을 기준으로 선수방향을 나타내는 회두각 ψ0, zb축에 대한 선회각속도(yaw rate) r을 정의하고 있다.
선박의 일반적인 운동은 6자유도로 묘사되지만 저속 조종운동의 경우에는 O - xbyb평면에서의 이동과 zb축의 회전을 가지는 3자유도 운동으로 근사 가능하다. 그러므로 오퍼레이터의 조작명령이 최대 고정속도 모드로 인식된 경우 통합제어시스템의 명령입력으로 설정되어야 하는 운동변수와 그 기준 값을 계산하는 식을 정리하면 Table 1과 같다.
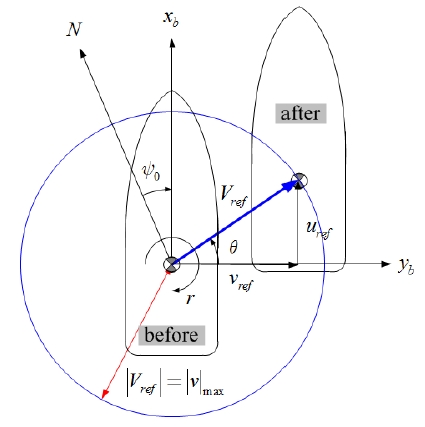
Definition of the maximal fixed speed mode with the magnitude of maximal sway velocity |Vref| = |ν|max
최대 고정속도 모드에서 자동으로 설정된 최대속도의 크기는 조이스틱의 방향각 θ에 관계없이 횡 방향의 최대속도의 크기 |ν|max로 제한되었다. 한편, 선박에서의 전진방향 속도의 크기는 CPP 추력 범위에서 얼마든지 조정 가능하다.
최대 가변속도 모드는 횡 방향의 속도의 크기를 조이스틱의 방향각 θ의 임의구간에서는 횡 방향의 최대속도의 크기 |ν|max로 고정하고 전진방향 속도의 크기를 조이스틱 방향각 θ에 따라 가변시킴으로써 설정된 최대속도를 가변시키는 모드로 정의된다. 이 때, 조이스틱의 방향각 θ에 의존하여 전진방향 속도의 최대크기도 제한된다. Figure 5는 최대 가변속도 모드 중에서 조이스틱의 방향각 θ가 구간 ① 또는 ③ 내에 있을 때의 모드에 대한 최대속도를 설정하는 방법을 묘사한 것이고, 이 모드에서의 이동명령을 수행하는데 필요한 명령변수들을 보여 주는 그림이다.
Figure 5와 같이 최대속도의 크기가 자동 설정되는 최대 가변속도 모드 명령에 대하여 선박이 이동운동을 수행하는데 입력되어야 하는 통합제어시스템의 명령변수와 그 기준 값을 계산하는 식을 정리하면 Table 2와 같다.

Command input variables and computation equations for maximal variable speed mode with joystick direction θ
이를 구체적으로 설명하면 조이스틱 방향각 θ에 따라 선박이 우현방향으로 이동할 때 즉 sgn(cosθ) =+1일 경우에는 νref = |ν|max로, 선박이 좌현방향으로 이동할 경우 즉 sgn(cosθ) =-1일 경우에는 νref = |ν|max로 항상 먼저 설정한 다음, 전진 또는 후진방향의 속도를 uref = νreftanθ로 설정함으로써 최종적으로 무게중심의 이동속도의 크기를 로 설정하는 방법이다. 따라서 설정되는 최대 가변속도는 θ의 방향에 따라 ① 또는 ③영역의 외곽을 따라 그 크기가 설정됨을 알 수 있다.
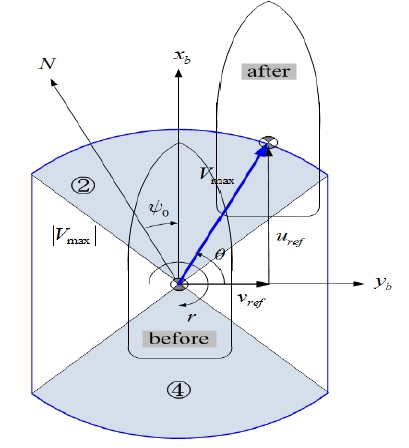
만약 조이스틱의 방향각 θ가 Figure 6과 같이 구간 ②와 ④ 내에 있을 때에는 선박 이동속도의 최대크기 |Vmax|가 상수로 가장 먼저 설정되며, 이 때 이동속도의 선수방향 성분 uref와 횡 방향 성분 νref는 |Vmax|와 조이스틱의 경사방향 θ에 의해 결정된다.
Table 3은 조이스틱 방향각 θ가 ② 또는 ④의 영역에 있을 때 이동명령을 수행하기 위한 통합제어시스템의 입력 명령변수와 그 기준 값을 계산하는 식을 정리한 도표이다.

Command input variables and computation equations for maximal variable speed mode with joystick direction θ
Table 3에서 기준 값을 계산하기 위하여 먼저 설정되어야 하는 |Vmax|의 설정방법을 구체적으로 설명하면, 횡 방향 최대속도의 크기를 |νref|max = |ν|max로 설정한 다음, |uref|max = |u|max = | |ν|maxtanθ |로 계산되는 선수방향 이동 최대속도의 크기를 조종운동에 대응하는 크기로 제한함으로써, 로 설정하는 것이다.
가변속도 모드는 설정속도 모드 내에서 이동명령에 대한 속도의 크기가 조이스틱 경사각 ζ의 함수로 가변되도록 정의하는 모드로서, 설정된 최대속도가 최대 고정속도인가 최대 가변속도인가에 따라 가변되는 속도크기가 결정된다.
Figure 7은 최대 설정속도 모드 내에서 오퍼레이터에 의해 조작된 조이스틱의 경사각 ζ의 함수로 선박의 이동속도 크기를 가감시키는 가변속도 모드를 정의한 그림이다.
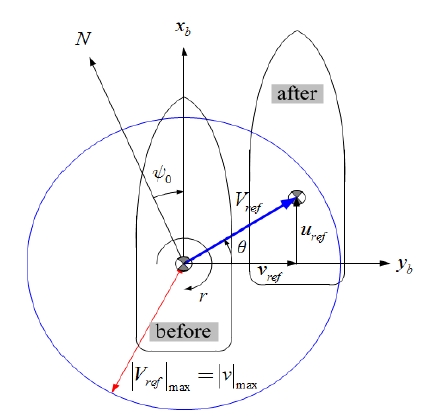
Variable speed mode under the maximal fixed speed | Vref|max = |ν|max with joystick direction θ and angle ζ
Figure 7에서 보는 바와 같이 모든 θ에 대하여 선박 이동속도의 최대크기는 | Vref |max = |v|max이며, 조이스틱 경사각 ζ에 따라 이동속도의 크기는 0 ≤ | Vref | ≤ |v|max 범위를 가지고 ζ에 비례하는 가변속도 모드이다. 조이스틱 방향각 θ와 조이스틱 경사각 ζ에 따른 선박이동을 위한 제어시스템 명령입력으로 작용하는 선박운동변수와 그 기준 값 계산식은 Table 4와 같이 정리된다.

Command input variables and computation equations for variable speed mode corresponding to Figure 7 with joystick direction θ and angle ζ
한편, 3.2.2절에서 설명한 바와 같이 최대속도가 조이스틱 방향각 θ에 따라 가변되어 설정되는 최대 가변속도 모드 내에서, 조이스틱의 경사각 ζ에 따라 최대속도가 가변되는 가변속도 모드는 조이스틱의 방향각 θ가 위치한 영역에 따라 2가지 모드로 다시 나뉜다.
조이스틱의 방향각 θ가 ① 또는 ③ 영역에 놓인 경우 속도명령을 설명하는 그림은 Figure 8이고, 이 모드에서 선박이동을 위한 제어시스템 명령입력으로 작용하는 선박운동변수와 그 기준 값 계산식을 정리하면 Table 5와 같다.
조이스틱의 방향각 θ가 ② 또는 ④ 구간에 놓인 경우 속도명령을 설명하는 그림은 Figure 9이고, 이 모드에서 선박이동을 위한 제어시스템 명령입력으로 작용하는 선박운동변수와 그 기준 값 계산식을 정리하면 Table 5와 동일하다다. 다만 Figure 8의 경우 | Vref |max의 크기가 조이스틱 방향각 θ에 따라 가변되는 것과 달리, Figure 9의 경우에는 최대속도 가 상수로서 정의되는 것이 다르다.
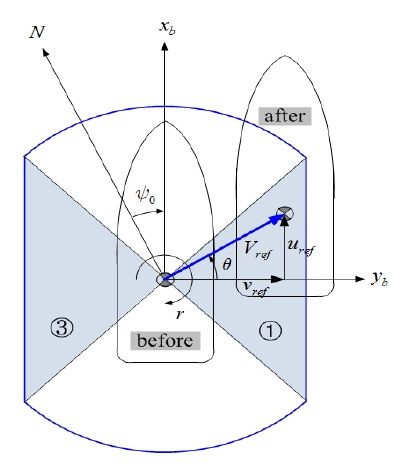
Variable speed mode under the maximal variable speed |Vref|max=|uref|2+|υ|max 2 with joystick direction θ and angle ζ

Command input variables and computation equations for variable speed mode corresponding to Figure 7 with joystick direction θ and angle ζ
3.3 요구 선가속도와 요구 각가속도 계산
이동운동에 대한 오퍼레이터의 조이스틱 조작명령 인식의 결과와 선박에 설치된 추력장치의 능력을 감안한 명령속도 운동변수와 그 기준 값을 선박이 추종하기 위해서는, 선박의 추력장치가 종합적으로 발생해야 할 추력을 계산해야 한다. 3자유도 저속 조종운동의 경우에는, 명령된 속도로 이동을 하기 위한 xb축과 yb축에 대한 추력을 계산하여야 하고, 이동운동 도중에 발생할지도 모를 회두각 변화를 방지하기 위한 zb축에 대한 추력모멘트를 계산하여야 한다. 이와 같은 요구추력과 요구 추력모멘트를 계산하기 위해서 선행되어야 하는 것이 바로 현재 샘플링 시간에서의 xb축과 xb축에 대한 요구 선가속도 , 과 zb축에 대한 요구 각가속도 을 계산하여야 한다.
요구 선가속도와 요구 각가속도는 계산된 운동명령 변수의 기준 값 즉 속도명령 값과 측정된 선박의 현재속도를 이용하여 매 샘플링시간마다 계산할 수 있다. 이때 가속도는 시간에 따라 계속 변하지만 샘플링시간 동안은 일정하다는 가정 하에 샘플링 주기 동안의 평균가속도를 계산하여 사용하는 것이 타당하다.
nTs시각에서 xb축 방향 기준명령 속도가 uref이고 선박의 현재속도가 u(n)일 때, xb축 방향 평균 가속도 은 Equation (1)에 의해 구할 수 있다.
| (1) |
nTs 시각에서 yb축 방향 기준속도가 νref이고 선박의 현재속도가 ν(n)일 때, yb축 방향 평균 가속도 은 Equation (2)로부터 구할 수 있다. 여기서, Ts는 샘플링 시간이다.
| (2) |
nTs 시각에서 zb축에 관한 선회방향의 기준 회두각이 ψref, 현재 회두각이 ψ(n)일 경우 zb축에 관한 선회방향 기준 각속도 rref(n)과 선박의 각속도 rs(n)은 Equation (3)으로 계산된다.
| (3) |
이때 zb축에 대한 평균 각가속도 은 Equation (3)을 토대로 Equation (4)로부터 계산된다[14].
| (4) |
| (5) |
| (6) |
한편, nTs 시각에서 선박의 회두각 ψ(n)이 선박의 기준 회두각 ψref와 같지 않을 경우에는 회두 각가속도를 Equation (4)와 같이 평균 각가속도로 설정하고, 같을 경우에는 현재 샘플링시간 nTs에서 선박의 회두각속도 rs(n)이 0 인가에 따라 Equation (5)와 Equation (6)으로부터 을 계산한다.
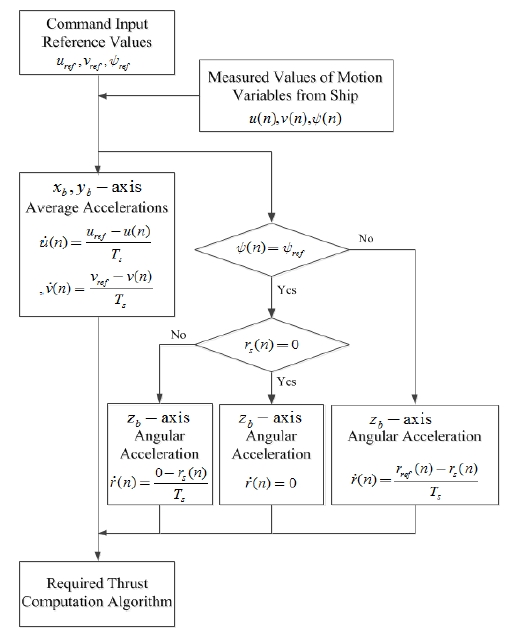
Figure 10은 오퍼레이터에 의해 내려지는 운동명령 모드별 명령입력 변수의 기준 값과 현재의 선박운동으로부터 측정된 운동변수 값을 이용하여 xb, yb축에 대한 평균 선가속도와 zb축에 대한 평균 각가속도를 구하는 알고리즘의 흐름 선도를 도시한 것이다.
3.4 요구 추력과 요구 추력모멘트의 계산
현재 선박이 가져야 하는 운동을 발생시키기 위해서는 추력장치가 발생시켜야 할 선박의 운동 축 xb, yb축에 대한 요구추력과 zb축에 관한 요구추력모멘트를 계산하여야 한다. 이를 위해서는 선체 자체의 관성력과 관성모멘트는 물론 선체주위 유체운동으로 인한 부가질량 관성력 및 관성모멘트, 유체 점성력 및 점성모멘트 등을 종합적으로 고려하여야 한다. 본 논문에서는 선박이 저속 조종운동을 하고 있다는 가정 하에 3자유도 비선형 선박운동방정식을 요구추력과 요구추력모멘트를 계산하기 위한 기본 식으로 사용한다고 가정한다.
고려하는 대상선박은 좌우 대칭이고 선박의 무게중심 상에 선체고정좌표계의 원점이 놓인다고 가정하며, 3차원 평면운동으로 가정하였기 때문에 유체 정역학적 관점에서의 복원력을 무시한다고 가정한다. 또한 O-xbyb평면 조종운동의 경우 선속도는 u, ν만을 고려하고 각속도는 r만을 고려하면 되므로 선수방향과 횡 방향, 요 방향의 운동만이 서로 연성되어 있다고 가정한다. 뿐만 아니라, 저속운동이므로 고속에서 발생하는 비선형 2차 감쇠 항을 무시한다면 Equation (7) - (9)와 같이 선박운동방정식을 근사하여 나타낼 수 있다[2][8].
| (7) |
| (8) |
| (9) |
여기서 m은 선체의 질량, 은 유체운동으로 인한 부가질량과 모멘트이고, Yν, Yr, Yδ, Nν, Nr, Nδ는 유체력 미계수(hydrodynamic derivative), XC, YC, NC는 추력장치에 의해 선박에 인가되는 추력과 추력모멘트이다.
한편, 선박 통합제어시스템에서는 운동 축에 대한 운동변수의 기준 명령 값을 추종하도록 제어하기 위하여 추력장치가 발생시켜야 할 요구추력 XC, YC와 요구추력모멘트 NC를 구하는 것이 필요하다.
따라서 상기의 식을 XC, YC, NC에 대하여 풀고 현재시간 t = nTs에서의 선박운동과 요구되는 선가속도 및 각가속도를 토대로 다음 샘플링시간 t = (n+1)Ts에서의 요구추력 Xc(n+1), Yc(n+1)와 요구추력모멘트 Nc(n+1)를 구하기 위한 순환알고리즘의 형태로 변환하면 Equation (10),(11) 및Equation (12)와 같다[15].
| (10) |
| (11) |
| (12) |
여기서 u(n), ν(n), rs(n)은 샘플링시간 nTs에서의 선박으로부터 측정되는 선속도 및 각속도이고 δ(n)은 타각이다. , ,은 속도명령 기준 값들을 추종하기 위하여 샘플링시간 nTs에서 선박이 가속되어야 하는 요구 선가속도와 각가속도이고, 는 선박이 현재 운동하고 있는 선가속도와 각가속도이다.
따라서 이동운동에 대한 속도명령의 기준 값을 추종하기 위하여 필요한 요구 가속도와 각가속도를 현재 선박의 가속도와 각가속도와 비교함으로써 부가적으로 선박에 인가시켜야 하는 요구추력과 요구 추력모멘트를 상기의 식에 의해 계산할 수 있다.
3.5 이동명령 수행을 위한 추력 할당 알고리즘
Equation (10)-(12)에서 계산되는 요구추력과 추력모멘트는 조이스틱 이동명령을 수행하기 위하여 필요한 선박의 운동 축 xb, yb축에 대한 요구추력과 zb축에 관한 요구 추력모멘트이다. 선박에 설치된 다 추력장치들이 동시에 작동한다고 가정할 때 이들이 발생하는 추력과 추력모멘트의 합이 정상상태에서 계산된 요구추력과 추력모멘트가 되기 위해서는 계산된 추력과 추력모멘트를 다 추력장치로 할당하는 방법이 필요하다.
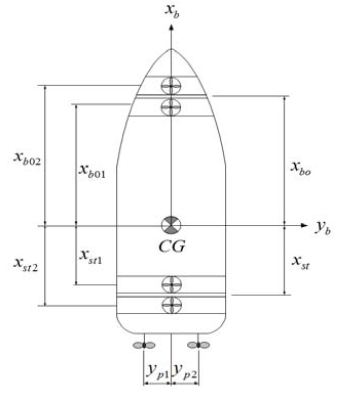
본 논문에서 고려하는 대상선박의 다 추력장치와 이들이 설치된 위치는 Figure 11과 같다고 가정한다.
또한 요구추력과 요구 추력모멘트를 추력장치에 할당하기 위하여 대상선박에서 고려해야 하는 전제조건과 선박제원은 다음과 같다고 가정한다.
(1) 선박에 설치된 모든 추력장치는 활성화되어 있다.
(2) xb축의 요구추력 XC(n+1)은 CPP 2개에 의해서만 발생되고 동일한 크기로 발생된다.
(3) CPP의 설치위치는 좌우대칭 즉 yp1 = yp2이다. 따라서 CPP에 의한 추력은 zb축에 관한 모멘트를 발생시키지 않는다.
(4) yb축의 요구추력 YC(n+1)은 선수 및 선미 측 사이드 쓰러스터에 의해서만 발생된다.
(5) 선수 측 사이드 쓰러스터에 의해 발생되어야 하는 요구 추력모멘트는 2개의 사이드 쓰러스터에 동시에 배분된다.
(6) 선미 측 사이드 쓰러스터에 의해 발생되어야 하는 요구 추력모멘트는 2개의 사이드 쓰러스터에 동시에 배분된다.
위와 같은 가정 하에 요구추력 및 요구 추력모멘트를 할당하기 위한 대수 연립방정식은 Equation (13)과 같다.
| (13) |
여기서 xst, xst1, xst2는 (-)값이고 xbo, xbo1, xbo2는 (+)값으로 Figure 11에서 보는 바와 같이 무게중심으로부터 사이드 쓰러스터가 설치된 위치까지의 거리이다. 그러므로 Equation (13)을 연립함으로써 각 추력장치에 할당될 추력은 Equation (14)와 같이 유도된다. 이때 Tcpp1 등은 각 해당 추력장치에 할당된 추력이다.
| (14) |
여기서, Equation (14)의 각 계수들은 다음과 같다.
4. 통합제어시스템 성능확인을 위한 시뮬레이션 수행과 결과의 고찰
4.1 대상선박의 제원 및 유체력 미계수
본 논문에서 제안한 조이스틱 기반 선박 통합제어시스템의 타당성을 검증하기 위하여 시뮬레이션을 수행하였다. 대상 선박은 기존의 SR-108 컨테이너운반선의 선체를 기본으로 선미, 선수 측에 각각 Side thruster 2개 2조, CPP 2개, 1개의 Rudder를 가진 것으로 가정한 선박으로서 필요한 선박제원을 표시하면 Table 6과 같고, 이를 토대로 Equation (10)-(12)의 추력계산 식에서 필요한 각종 계수를 계산하면 Table 7과 같다[8].
한편, 본 논문의 목적은 조이스틱에 의해 내려진 이동운동 명령을 통합제어시스템이 잘 추종하는지 그 여부를 확인하는 것이다. 따라서 저속에서의 조종운동에 대한 본 논문의 시뮬레션에서는 CPP와 사이드 쓰러스터의 정격추력에는 제한을 두지 않고 속도명령을 정상상태에서 추종할 수 있도록 할당된 요구추력을 충분히 발생시킨다고 가정하였다. 또한 CPP와 사이드 쓰러스터의 동적특성을 반영한 수학모델은 고려하지 않음으로써 과도응답 발생 없이 할당된 추력을 즉시 표출하는 것으로 가정하였다.
4.2 성능확인을 위한 시뮬레이션 수행
조이스틱에 의해 내려진 선박의 이동명령에 대하여 통합제어시스템이 제대로 추종하는가를 평가하기 위하여 여러 가지의 시나리오를 가정하고 시뮬레이션을 수행하였다. 시뮬레이션을 위한 기본 벤치로는 Figure 12에 나타낸 바와 같이 매트랩 SIMULINK 기반으로 설계된 시뮬레이터를 활용하였다.
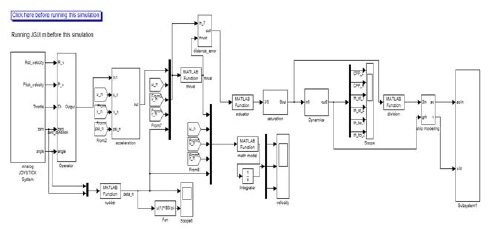
Simulator of the integrated control system for translational motion of ship designed using MATLAB Simulink
Figure 12에 표시된 매트랩 함수 블록 내에는 조이스틱 이동명령의 인식, 선가속도 및 각가속도의 계산, 요구추력의 계산, 추력할당, 3자유도 비선형 선박모델 등을 위한 알고리즘들이 매트랩 언어로서 프로그램 되어 있으며, 본 논문에서는 시뮬레이터 구성에 대한 구체적 언급은 생략하기로 한다.
조이스틱에 의한 이동명령이 Figure 4와 같이 최대 고정속도 모드로 인식되었을 경우 통합제어시스템의 이동명령 추종결과를 평가하기 위하여 시뮬레이션을 수행하였다. 초기 t=0[s]에 정지해 있던 선박을 이동시키기 위하여 t=10[s]에 조이스틱 방향각 180[o]로서 최대 고정속도 2[m/s]로 50[s]동안 이동하도록 하고 t=60[s]에 조이스틱 방향각을 다시 0[o]로 환원함으로써 이동을 멈추도록 하는 명령 시나리오이다. 이 시나리오에 의해 내려진 이동 명령변수와 기준 값은uref = 0[m/s]이고 νref =-2[m/s]이며 선수방향의 회두각 ψref = 0[0]이다.
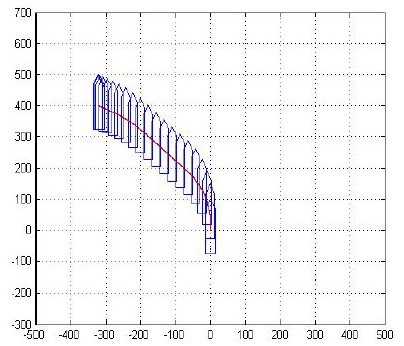
Figure 13은 상기 시나리오에 대하여 샘플링 시간을 Ts = 0.1[s]로 설정하고 통합제어시스템의 각 알고리즘들을 실행하여 이동명령을 수행한 선박운동의 시뮬레이션 결과이다. 가로축은 횡 방향 즉 yb축으로의 이동거리([m])이고 세로축은 전진방향 즉 xb축으로의 이동거리([m])이다. 초기에 (0, 0) [m]위치에서 정지하고 있던 대상선박이 선수방향의 회두각 변화 없이 (0, -100) [m]의 위치로 이동했음을 볼 수 있다.
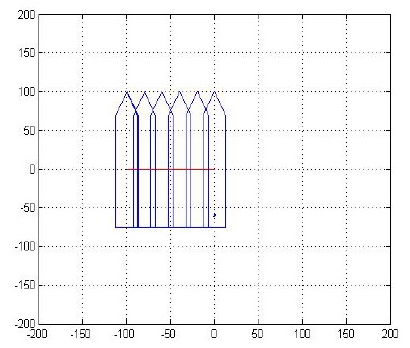
Ship motion result by the integrated control system for the translational command in pure sway direction
시나리오에 따라 수행된 결과를 구체적으로 나타내기 위하여, 조이스틱에 의한 이동명령 방향과 이동명령 속도는 물론, 통합제어시스템에 의해 계산된 요구추력과 추력모멘트, 실제 선박이 이동한 운동결과를 나타낸 그림은 Figure 14이다.
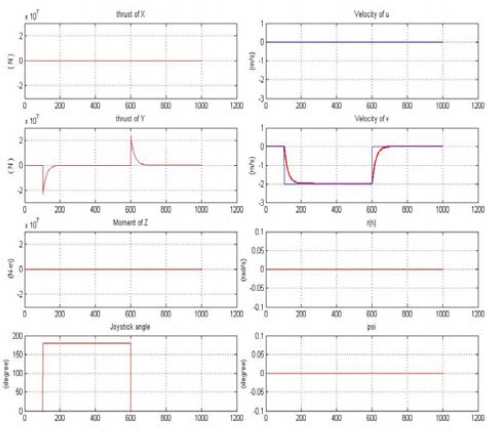
Joystick command, thrusts, and translational motion results of the ship under a maximal fixed speed command
Figure 14에서 가로 좌표축의 단위는 1[s]당 10번을 샘플링 한 샘플수로서 좌표 값을 나타내었으며, 속도를 표시한 선의 경우 파란 선은 조이스틱 명령에 따른 이동 명령속도를 나타낸 것이고, 빨간 선은 명령속도를 통합제어시스템에 의해 선박이 실제로 추종하여 이동한 속도를 도시한 것이다. Figure 13에서도 확인되는 바와 같이, t = [10, 60] [s]사이의 50[s]동안 횡 방향 속도명령만을 ν(n) = -2[m/s]로 정상상태에서 잘 추종하고 있고, 회두각속도 rs(n) = 0 [o/s]와 회두각 ψ(n) = 0[o]를 유지함으로써 선수방향 회전 없이 이동명령을 잘 수행하고 있음을 볼 수 있다.
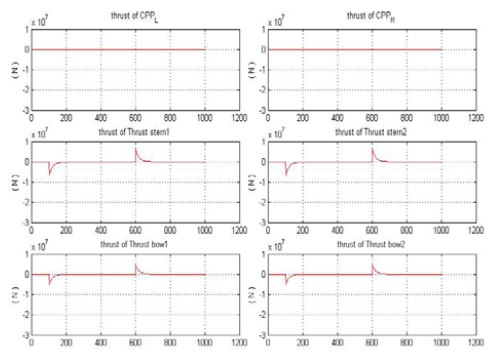
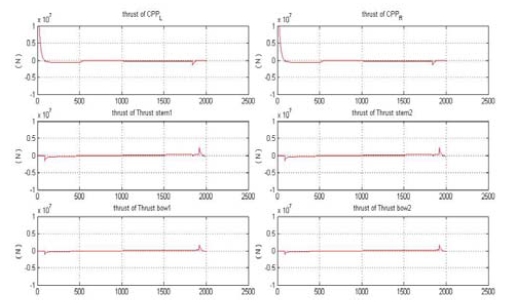
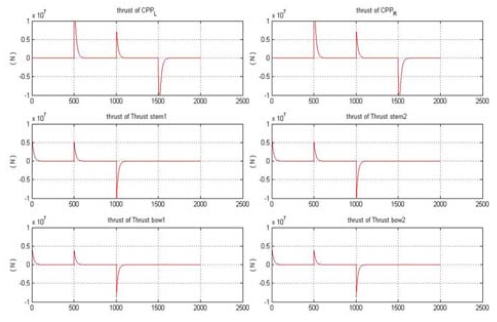
Figure 15는 시나리오에 의해 내려진 속도명령을 추종하기 위하여 Figure 14와 같이 계산된 요구추력을 추력할당알고리즘을 이용하여 선박의 다 추력장치에 할당한 결과를 나타낸 것이다. 그림에서 보는 바와 같이 요구추력은 선수 측 사이드 쓰러스터와 선미 측 사이드 쓰러스터에만 할당되어 횡 방향의 속도만 발생시키도록 동작하고 있음을 알 수 있다.
조이스틱에 의한 이동명령이 가변속도 모드로 인식되었을 경우 통합제어시스템의 이동명령 추종결과를 평가하기 위하여 시뮬레이션을 수행하였다. 초기시간 t=0 [s]에서 회두각 ψ0 = 0[o]를 유지하면서 정지해 있던 선박을 t = [0, 50] [s]동안은 Figure 7에서 정의한 가변속도 모드에 따라 이동시키고, t= [50, 100] [s] 동안은 Figure 9에서 정의한 ② 영역의 가변속도 모드에 따라 이동시킨 다음, t= [100, 150] [s] 동안은 Figure 8에서 정의한 ③ 영역의 가변속도 모드에 따라 이동하도록 시나리오를 구성하였다.
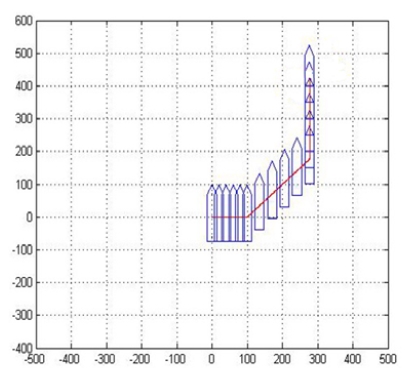
Figure 16은 상기의 시나리오에 따라 가변속도와 방향을 가지고 이동운동을 수행한 선박의 시뮬레이션 결과를 보여주는 그림이다. 그림에서 보는 바와 같이 선박의 이동속도와 방향이 명령된 조이스틱 방향각과 경사각에 따라 지속적으로 가변되고 있음에도 불구하고, 통합제어시스템에 의해 동작되는 선박은 선수방향에서의 회두각 변화 없이 이동운동에 대한 명령을 정상상태에서 잘 추종하고 있음을 확인할 수 있다.
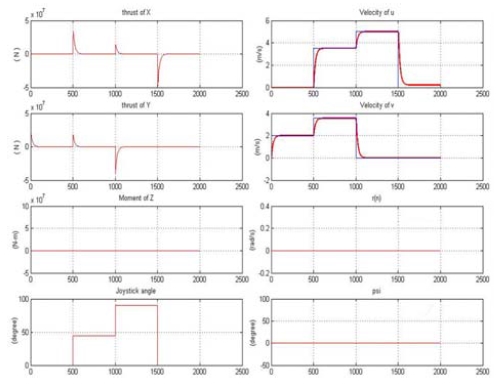
Figure 17은 선박의 이동운동을 제어한 통합제어시스템의 수행과정을 구체적으로 나타낸 것으로, 조이스틱의 이동명령 방향과 조이스틱 경사각에 따라 입력된 속도명령 기준 값 uref 및 νref, ψref을 추종하기 위하여 통합제어시스템에서 계산한 요구추력과 모멘트는 물론 선박이 실행한 실제 회두각속도와 실제 회두각을 나타낸 것이다.
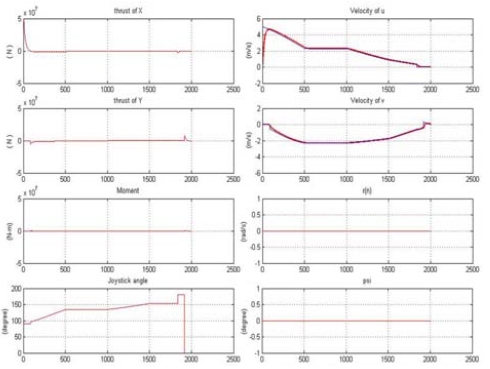
Joystick angle, required thrusts, and translational motion results under a set of variable speed commands
Figure 17에서 보는 바와 같이 선박의 회두각은 초기의 회두각 ψ0 = ψref = 0[o]를 유지한 채, 조이스틱의 방향각과 경사각에 따라 변하는 이동속도와 이동방향을 점근적으로 잘 추종하고 있음을 알 수 있다.
Figure 18은 내려진 속도명령을 추종하기 위하여 Figure 17과 같이 계산된 요구추력을 선박의 다 추력장치로 할당한 결과를 나타낸 것이다. 그림에서 보는 바와 같이 요구추력은 상황에 따라 CPP 2대와 선수 측 및 선미 측 사이드 쓰러스터에 적절하게 할당되었음을 알 수 있다.
실제 선박에서 발생할 수 있는 복합적인 이동운동을 가정하여 통합제어시스템의 이동운동 추종성능을 평가하기 위한 시뮬레이션을 수행하였다. 복합 이동운동에 대한 시나리오는, 정지하고 있던 선박이 t = [0, 50] [s]동안에는 최대 고정속도 모드로 전진속력 uref = 0 [m/s], 횡 방향 속력 νref = 2 [m/s], 회두각 ψref = 0 [o]를 유지하면서 이동하고, t = [50, 100] [s] 사이에는 최대 가변속도 모드 ① 영역에서 조이스틱 방향각 θ = 45 [o]일 때 전진속력 uref = 3.8 [m/s], 횡 방향 속력 νref = 3.8 [m/s], 회두각 ψref = 0 [o]로 이동한 다음, t = [100, 150] [s] 사이에는 최대 가변속도 모드 ② 영역에서 uref = 5.38 [m/s], νref = 0 [m/s] 회두각 ψref = 0 [o]로서 전진방향으로만 이동하고, t = 150 [s]에서 조이스틱을 원위치 시킴으로써 정지하도록 명령하는 시나리오이다.
Figure 19는 상기의 복합 이동운동 시나리오에 따라 선박이 이동한 결과를 도시한 것이다.
실제의 선박과 유사한 이동운동을 묘사하기 위한 복합운동 시나리오 명령에 대해서도 통합제어시스템은 각종 알고리즘을 계산하여 최종적으로 다 추력장치에 발생시켜야 할 추력을 적절히 할당함으로써, 회두각 변화 없이 명령된 이동운동을 잘 추종함을 알 수 있다. 통합제어시스템에서 생성된 요구추력과 추력모멘트, 속도명령과 이를 추종한 선박의 실제 속도 성분들을 도시한 것이 Figure 20이고, 다 추력장치에 할당된 추력을 도시한 것이 Figure 21이다.
4. 결 론
본 논문에서는 다 추력장치를 가진 선박을 대상으로 임의의 방향과 속도에서 이동명령을 수행할 수 있는 조이스틱 기반의 통합제어시스템 구성방법을 제안하였다. 통합제어시스템의 중요한 구성요소로서 조이스틱의 방향각과 경사각을 사용하여 다양한 속도명령을 생성하는 알고리즘을 제안하였고, 주어진 속도명령을 추종하기 위하여 필요한 운동변수의 정의와 이들이 가져야 하는 기준 값 생성방법을 제안하였다. 또한 정의된 운동변수의 기준 값을 추종하기 위해서 반드시 필요한 선가속도 및 각가속도 계산알고리즘을 비롯하여 요구추력 및 요구 추력모멘트 계산알고리즘, 이들을 다 추력장치에 할당하는 할당알고리즘 등 필수적인 모든 알고리즘들을 제안하였다. 또한 이동운동을 위해 제안된 통합제어시스템의 성능을 검증하기 위하여 매트랩 SIMULUNK 기반의 통합제어시스템 시뮬레이터를 구성하였고, 이를 활용하여 기본 이동운동에서부터 복합 이동운동에 이르기까지 여러 가지의 이동운동 명령에 대한 시뮬레이션을 수행하였다. 시뮬레이션으로부터 얻은 결과를 분석한 결과 선박의 이동운동 제어를 위하여 본 논문에서 제안된 통합제어시스템 구성방법이 기본 프레임으로서 매우 유효한 방법임을 확인하였다.
앞으로의 연구방향은 3차원 비선형 선박모델을 보다 현실성 있는 실제의 선박에 가깝도록 모델링하고, CPP와 사이드 쓰러스터에 대한 동적모델을 도입함으로써 실질적인 이동운동 통합제어시스템을 구성하여 그 성능을 확인하는 것이다.
References
- T. I. Fossen, Recent Development in Ship Control Systems Design, World Superyacht Review, Sterling Publication Limited, Millenium Edition, London, (2000).
- T. I. Fossen, “A survey on nonlinear ship control : From theory to practice”, Proceedings of the 5th IFAC Conference on Maneuvering and Control of Marine Craft, p1-16, (2000).
- Breivik, M., J. P. Strand, and T. I. Fossen, “Guided Dynamic Positioning for Marine Surface Vessels”, IFAC MCMC'06, Lisbon, Portugal, September 20-22, (2006), [Online]. Available: www.fossen.biz/home/papers/BreivikStrandFossen%20MCMC06.pdf.
- Lekkas, A. M., and T. I. Fossen, Line-of-Sight Guidance for Path Following of Marine Vehicles: Chapter 5, In Advance in Marine Robotics, LAP LAMBERT Academic Publishing., O. Gal, Ed.) p63-92, ISBN 978-3-659-41689-7 (2013).
- B. K. Lee, Optimal Route Decision and LOS Guidance System, Ph.D Dissertation, Korea Maritime University, (2005), (in Korean).
- B. K. Lee, and J. H. Kim, “A study on the automatic path tracking control of ship using adaptive fuzzy method”, Proceedings of the 14th Korea Automatic Control Conference, D, p21-24, (1999), (in Korean).
- B. K. Lee, J. H. Kim, D. Y. Kim, and T. H. Kim, “A study on the optimal path decision using genetic algorithm”, Proceedings of the 15th Korea Automatic Control Conference, 1, p255-258, (2000), (in Korean).
- K. H. Sohn, Y. M. Kim, “A study on mathematical model of manoeuvering motions of twin-screw and twin- rudder ship for construction of real-time ship handling simulator”, Journal of the Korean Society of Marine Environment and Safety, 7(3.), p1-16, (2001), (in Korean).
- S. H. Suh, Y. G. Song, “Study on the control algorithms for the auto-pilot system”, Transaction of the Society of the Naval Architects of Korea, 31(2), p38-44, (1994), (in Korean).
- J. H. Kim, J. K. Lim, and B. H. Choi, Development of the Ship Joystick Control System, Research Report Submitted in KTE Co. Ltd., Korea, (2009), (in Korean).
- K. H. Sohn, S. K. Lee, and S. P. Ha, “Mathematical model for dynamics of manta-type unmanned undersea vehicle with six degrees of freedom and characteristics of manoeuvrability response”, Transaction of the Society of the Naval Architects of Korea, 42(4), p399-413, (2006), (in Korean).
- B. K. Lee, and J. H. Kim, “Yaw angle command generation and adaptive fuzzy control for automatic route tracking of ships”, Journal of the Korean Society of Marine Engineering, 25(1), p199-208, (2001), (in Korean).
- J. H. Kim, J. E. Woo, S. H. Park, and J. K. Lim, “Translation control in integrated control system for ship steering motion”, Proceedings of the 38th Korean Society of Marine Engineering Spring Conference, 1, p197, (2014), (in Korean).
- J. J. Craig, Introduction to Robotics : Mechanics and Control, Pearson Edition, Prentice-Hall, (2005).
- K. Ogata, Modern Control Engineering, Pearson Edition, Prentice-Hall, (2003).