풍력 레저선박의 돛 받음각과 횡력에 대한 복원력 특성

1. 서 론

해양레저 인구가 늘어나면서 저비용으로 운용가능한 태양광, 풍력을 이용한 레저선박의 필요성이 부각되고 있다. 특히 풍력을 이용한 레저선박은 제작비용이 낮고 무한히 공급되는 풍력을 이용하기 때문에 운용상의 비용이 들지 않는 반면 안정성에 대한 문제점을 안고 있다. 따라서 풍력 레저선박의 안정성은 인명과 직결되므로 반드시 확보되어야 한다. 특히나 풍력에 의한 복원력은 횡력에 의해 레저선박의 안정성 확보는 필수적이다. 레저선박과 같은 선박의 안정성에 관한 연구로는, Yoshimura 등[1]은 풍력 에너지를 이용하여 추진력을 향상 시키는 것과 함께 부가적인 효과는 선체의 동요를 감소시킨다는 연구결과를 발표하였다. 또한, Masuyama 등[2]은 고속선이 항주 시 돛의 각의 제어를 통해 횡동요가 감소한다고 보고하였다. Chae 등[3]은 선박횡동요제어에 관해 실험연구를 하였으며, Jeong 등[4]은 고속선에 대한 저항성능에 주안점을 두고 연구한 바가 있다. 그리고 Kim 등[5]은 횡요방지장치에 대한 실험과 시뮬레이션을 통해 횡요저감효과를 검증하였고, Lee 등[6]은 단순한 형상인 바지선에 대한 파랑 중 횡요감쇠운동에 관하여 실험과 해석을 통해 안정성 해석을 한 연구사례를 찾아볼 수가 있다.

그러나 선행연구에서는 선박의 복원성과 횡요감소에 대한 연구가 일부 수행되었으나, 풍력선박의 받음각 및 횡력에 의한 안정성에 대해서는 거의 연구되지 않았다. 풍력을 이용한 레저선박의 경우, 돛의 방향을 변경함으로써, 돛의 받음각이 변경되고, 이것은 항력과 양력의 변화뿐만 아니라, 추력과 횡력도 변하게 된다. 횡력은 풍력선박의 안정성에 중요한 영향을 준다. 따라서, 본 논문에서는 풍력선박에 대해서 받음각과 횡력에 의한 선박의 복원성을 평가하였다. 받음각에 따른 힘을 유체해석을 통해서 구하였고 복원성 평가를 위한 추력과 횡력식을 유도하였다. 돛의 영향 및 받음각에 따른 복원성을 평가하였다.

2. 이론적 배경

유체해석을 위한 지배방정식은 Equation (1)과 Navier’s Stocks Equation (2)를 사용하였다.

Equation (1) 과 Equation (2)에서 U_i는 평균속도의 유속성분을 나타내며 P는 평균압력, u_i, u_j는 속도를 나타낸다.

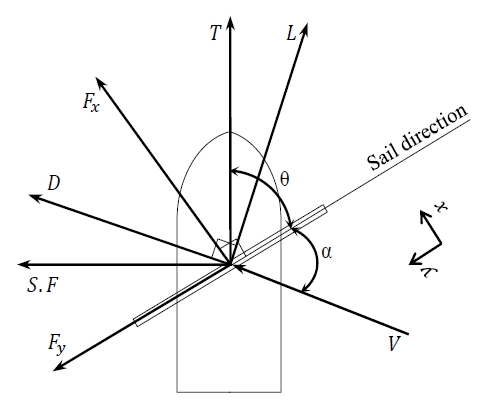
풍력 선박의 추력과 횡력을 유체해석과 연계하여 구하기 변수들간의 상관관계를 Figure 1에 나타내었다. 여기서, α는 받음각, θ는 추력과 돛이 이루는 각이다. V, L, D, T, S.F는 각각 풍향, 양력(Lift), 항력(Drag), 추력(Thrust), 횡력(Side Force)을 나타낸다. 또한, x, y좌표계는 유체해석에서 사용될 국부좌표계로서 돛의 법선방향을 x, 돛의 접선방향을 y로 둔다. 유체해석으로부터 x, y방향의 하중을 구하게 되는데 이때 x방향, y방향의 하중을 각각 F_x, F_y라 한다. 양력(L)과 항력(D)을 F_x, F_y의 항으로 표현하면 Equation (3)으로 쓸 수 있다.

Figure 1:

Relations among variables and angles such as angle of atta (AOA, α) and θ

추력(T), 횡력(S.F)을 F_x, F_y의 항으로 표현하면 Equation (4)로 쓸 수 있다.

Equation (3), Equation (4)에 의해서 추력(T), 횡력(S.F)을 양력(L)과 항력(D)의 항으로 표현하면 Equation (5)로 쓸 수 있다.

돛을 단 선박의 복원성을 실제 상태에서 정확하게 계산하는 것은 불가능 하다. 왜냐하면 돛의 모양, 돛을 다는 방법 등 여러 요소가 복원력에 영향을 주기 때문이다. 따라서, 본 논문에서는 복원성을 평가하기 위해 다음과 같이 간단한 상태를 가정 하였다.

1) 돛은 평면이고 바람은 일정하게 불어온다.

2) 풍압중심(Center of Effect: C.E.)은 돛 모양의 도심에 놓여 있다.

3) 배의 침수 표면에 작용하는 수압중심(Center of Lateral Resistance: C.L.R.)은 타를 포함한 배의 중앙 종단면의 수선하면적의 중심에 놓여있다.

C.E.와 C.L.R. 사이의 거리를 h라 하면S.F에 의한 횡경사 모멘트 M_w는

이며 복원 모멘트 M_ϕ와 평형을 이루게 된다.

따라서, Equation (6), Equation (7)에 의해서

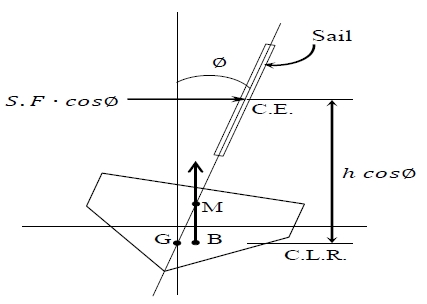
즉 풍압에 따른 선박의 횡경사(ϕ)는 횡력(S.F), 풍압중심과 측압 중심간의 거리(h)에 비례하고, 배수량(∆)과 메타센터 높이(GM)에 반비례한다. 풍압에 의해 Figure 2와 같이 선박이 경사(S.F)졌을 때의, 횡경사 모멘트 M_w, 복원 모멘트 M_ϕ는 다음과 같다.

Figure 2:

Side force and heel of boat with sail

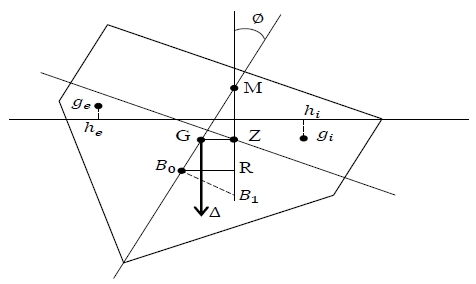
Equation (10)의 복원 모멘트는 10° 미만의 횡경사에서 적용이 되며 Equation (7), Figure 3과 같이 10°를 초과하는 횡경사에서는 메타센터 M가 경사각에 따라서 다른 점으로 이동하기 때문에 M_ϕ는 다음과 같이 나타낼 수 있다.

Figure 3:

Schematic view of boat with heel (ϕ) over 10

여기서, ν는 선박이 기울어짐에 따라 침하된 체적과 노출된 체적이다. Equation (11b)의 앞 항 ∆(ν·h_eh_i)/∇은 선체의 수면 하에 잠긴 부분의 형상과 관련된 형상복원력이고, 뒤 항 ∆·B₀Gsinϕ은 무게 중심의 위치와 관련된 중량 복원력이다. 따라서 복원 모멘트는 형상복원력에서 중량복원력을 뺀 값이 된다.

3. FEM 유동 해석

3.1 해석대상모델

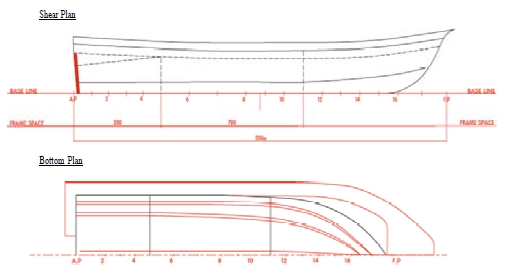
해석에 사용된 선박 모델은 소형 레저선박으로 Table 1에 주요제원을 정리하였으며 Fig. 4에 단순화된 선박의 도면을 나타내었다. 본 연구에서는 돛의 마스트에 연결된 선박이 해석 결과에 영향을 미치지 않는다고 가정하여 폭 0.6m, 길이 1.25m인 돛에 대한 유체 해석을 진행하였다.

Table 1:

Principal dimension of design boat

Figure 4:

Shear plan and bottom plan of analysis boat model

3.2 격자생성

격자 품질을 향상시키기 위하여 벽 근처의 격자는 삼각기둥(prism) 형태로 설정 하였으며, 블레이드 표면의 격자크기를 조절하여 실험 모델 주위의 밀집도를 향상시켰다. Figure 5에 보인 바와 같이 격자생성은 ANSYS Workbench CFX-Mesh를 이용하였으며, 전체 격자점은 대략 670,000개 가 생성되었다.

Figure 5:

Fluid field mesh of analysis

3.3 ANSYS Workbench CFX-Mesh 해석

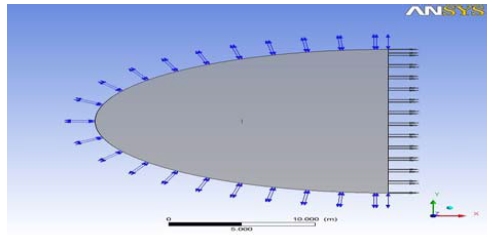
Sail 주변의 공력특성 파악을 위해서 받음각이 5°에서 90°까지 5°간격으로 해석할 수 있는 해석 모델을 Figure 6과 같이 생성하였다. 좌표계는 Figure 1에 보인바와 같이 돛의 법선방향을 x, 돛의 접선방향을 y로 두었다. 돛의 방향과 x, y방향은 고정으로 두고 풍향이 변경되도록 하였다.

Figure 6:

Boundary condition of analysis model

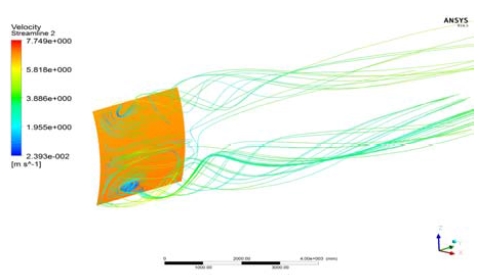
입구에서의 풍향조건은 균일 속도로 5 m/s를 각도에 따라 유입하고 나갈 수 있도록 열린(opening) 조건을 설정하였으며, 출구 조건은 평균 정압(average static pressure)을 대기압과 같게 놓았다. 점성 유동의 해석이므로, Sail 표면에서는 점착 조건(no-slip condition)으로 처리하였다. Figure 7는 이러한 경계 조건이 원방에서 잘 적용되고 있는지 확인하기 위하여 유선과 속도를 도시하였다(θ = 30^o).

Figure 7:

Computational domain and boundary condition (Check for streamlines)

확인 결과, 비대칭적인 계산 영역에도 불구하고 유동 입사 각도가 후류에서 잘 유지되며, 평균 입사 속도 또한 5 m/s로 고정되고 있음을 알 수 있었다. 받음각은 30~90도로 변동시키면서 공력 계수 값을 관찰하였다. Figure 8에서 돛은 위아래가 좌우보다 긴, 홀쭉한 형태이기 때문에 깃 끝 와류(wing-tip vortex)가 세로로 배열된 형태를 보여준다. 물론 가로로 배열된 깃 끝 와류도 동시에 관찰되어서 전체적으로는 3차원적인 복잡한 와류 구조를 보여준다.

Figure 8:

Velocity field and streamline of rectangular sail

3.4 유동해석결과

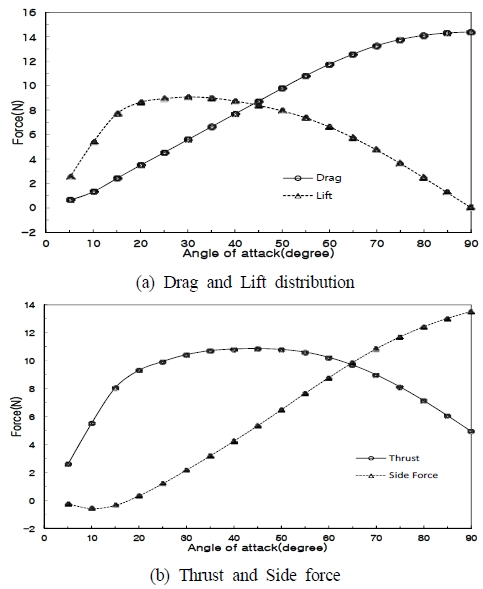
유동해석을 수행하였고, 유동해석에서 구한 항력(D)과 양력(L)을 받음각에 대해서 정리하면 Figure 9(a)와 같다. 받음각이 증가함에 따라 항력(D)은 증가한다. 양력(L)은 받음각이 30°까지 가파르게 증가한 후 완만하게 감소한다. 추력과 횡력의 일반식은 Equation (3), Equation (4)와 같으며, 본 연구에서는 예시를 위하여 풍향이 일정하고 풍향과 추력방향사이의 각(β)이 일정하다고 가정하였다. 이것을 수식화하면 다음과 같다.

Figure 9:

Force distribution according to angle of attack

$\[ {\displaystyle \beta =\alpha + \theta } \]$

(12)

여기서, β 상수이며 110°로 두었다. Equation (12)을 θ에 대해 정리하면 Equation (13)와 같다.

$\[ {\displaystyle \theta ={110}^{\circ }-\alpha } \]$

(13)

Equation (13)를 Equation (4)에 대입하여 Equation (14)를 얻었다.

$\[ {\displaystyle \left\{\begin{array}{c}T\\ S.F\end{array}\right\}=\left[\begin{array}{cc}\sin ({110}^{\circ }-\alpha )& -\cos ({110}^{\circ }-\alpha )\\ \cos ({110}^{\circ }-\alpha )& \sin ({110}^{\circ }-\alpha )\end{array}\right]\left\{\begin{array}{c}{F}_x\\ F_y\end{array}\right\}} \]$

(14)

이것을 그래프로 그리면 Figure 9(b)와 같다. 받음각이 증가함에 따라 S.F는 계속 증가하고, T는 45°를 정점을 이루고 감소하는 것을 알 수 있다.

4. 풍력 레져 선박의 복원력평가

4.1 돛에 의한 복원력 영향평가

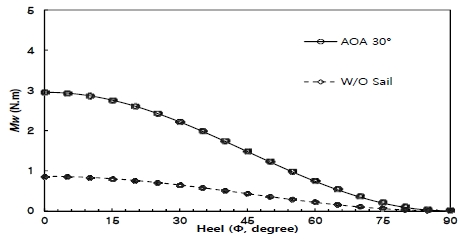
돛이 선박의 복원력에 주는 영향을 평가하기 위해 돛이 없는 경우와 있는 경우의 복원력을 비교하였다. 먼저 돛이 없는 경우, 풍압은 선박의 측면에 작용하여 횡경사가 발생한다. 풍향과 추력사이의 각은 Equation (12)에서와 같이 110°이며, 풍속 5m/s로 작용한다. 선박의 측면에 작용하는 풍속은 Vcos(20°) = 4.69m/s가 된다. 횡경사 모멘트 M_w는 Equation (6)을 사용하였다. Figure 10는 돛이 없는 경우와 돛이 있는 경우 받음각 30°일 때의 횡경사 모멘트를 보여준다. 돛이 없을 때의 횡경사 모멘트에 비해 3배 이상의 모멘트가 작용함을 알 수 있다.

Figure 10:

Comparison of heel moment (Mw) of boat W/T and W/O sail

4.2 받음각에 따른 복원력 평가

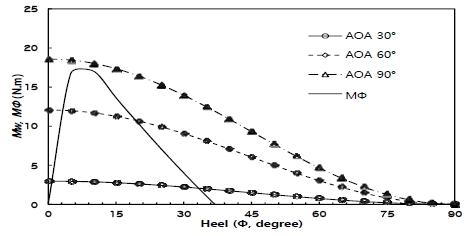
받음각 별로 선박의 복원력을 평가하기 위해, 받음각 30°, 60°, 90°일 때의 횡경사 모멘트 M_w와 복원모멘트 M_ϕ를 계산하였다. 횡경사 모멘트의 식은 Equation (9)을 사용하였고, 받음각별 횡력 S.F는 Fig. 9의 ANSYS해석결과를 사용하였다. 복원 모멘트 M_ϕ의 식은 경사각 10° 미만, 10° 이상인 경우, 각각 Equation (10), Equation (11)을 사용하였다. Figure 11에 보인 바와 같이 받음각이 30°, 60°, 90°로 증가함에 따라 횡경사 모멘트가 증가하는 것을 알 수 있다. 복원모멘트는 10°부근 까지 증가한 후 40°부근에서 소멸하는 것을 알 수 있다. 또한, 받음각이 60°까지는 복원모멘트 값이 횡경사모멘트보다 높은 값으로, 선박의 복원성이 있다고 할 수 있으나, 받음각이 90°에서는 횡경사 모멘트의 그래프가 복원모멘트의 그래프의 위쪽에 있으므로 선박은 전복된다. 따라서, 선박의 안정성을 위해 받음각이 60°를 넘지 않는 것이 좋다고 할 수 있다.

Figure 11:

Heel moment (Mw) according to angle of attack(AOA) 30°, 60°, 90° and restoring moment (Mϕ)

4.3 레져선박의 복원력 평가

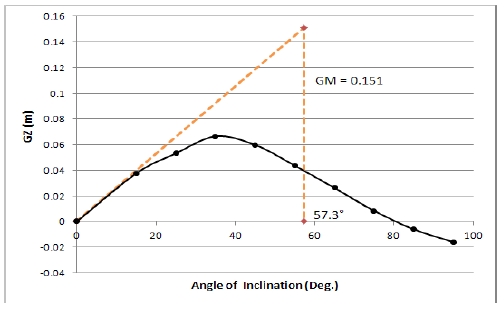
풍력 레저선박의 복원력 특성을 알기 위하여 횡경사각에 따른 복원정(GZ)을 Equation (15)에 의해 조사하여 Table 2에 정리하였고 Figure 12에 정적 복원력 곡선으로 나타내었다. Figure 12에서 풍력 레져선박이 횡경사시 복원력 특성 을 나타내고 있으며 GM은 0.151로 산정되며 한계경사각은 약 35°로 나타났다.

Table 2:

GZ value according to angle of inclination

Figure 12:

Static restoring curve of leasure boat

이 한계 경사각 이상으로 풍력 레져선박이 바람 등의 외력에 의해 경사지게 되면 선박은 복원력을 상실하여서 전복하게 되므로 설계시에 주의하여야한다.

$\[ {\displaystyle GZ=KN-KG\cdot \sin \varphi } \]$

(15)

4. 결 론

돛을 단 레저선박에 풍하중이 작용하였을 때 선박의 안정성을 평가하기 위해 복원력을 평가하였다. 복원력 평가를 위해 받음각과 고려한 횡력과 추력을 수식화 하였고, 횡력에 의한 횡경사모멘트, 복원모멘트를 유도하였다. 유동해석을 이용해 구한 횡력값을 사용하여 복원력을 평가하였고 다음과 같은 사실을 알 수 있었다.

추력의 방향과 바람의 방향이 일정할 때, 받음각이 증가함에 따라 횡력은 증가한다. 돛을 달았을 때의 횡경사 모멘트는 돛을 달지 않았을 때보다 큰 값을 보인다. 돛을 단 경우에 받음각이 증가함에 따라 횡경사 모멘트는 증가하며, 복원모멘트보다 큰 값에서는 선박은 전복된다. 또한 풍력 레져선박의 횡경사시 복원력 특성을 조사한 결과, 전반적으로 GM은 0.151로 산정되었으며 한계경사각은 약 35°로 나타났다.

이 한계 경사각 이상으로 풍력 레져선박이 바람 등의 외력에 의해 경사지게 되면 선박은 복원력을 상실하여서 전복하게 되므로 설계시에 주의하여야한다. 본 연구의 결과는 돛을 단 레저선박의 설계에 반영할 수 있을 것으로 사료된다.

Acknowledgments

본 연구는 교육부와 한국연구재단의 지역혁신인력양성사업으로 수행된 연구결과 (No. 2013H1B8A2023237)와 2013년도 호남광역경제권 선도산업 산업생태계 지원 사업(그린, 레저 선박 기자재 개발을 위한 기술 인력 지원)의 지원으로 연구되었습니다.

References

• Y. Yoshimura, T. Kuroda, M. Kikumoto, and Y. Igarashi, “Roll-damping control by sail-angle”, Journal of the Society of Naval Architects of Japan Symposium Proceeding 2, p85-86, (2003), (in Japanese).
• Y. Masuyama, I. Nakamura, H. Tatano, K. Takagi, and T. Miyakawa, “Sailing performance of ocean cruising yacht by full-scale sea test Part 1 : Steady sailing performance and dynamic performance in waves”, Journal of the Society of Naval Architects of Japan, 172, p349-364, (1992), (in Japanese). [https://doi.org/10.2534/jjasnaoe1968.1992.172_349]
• G. H. Chae, and Y. B. Kim, “An experimental study on the rolling motion control of a ship based on LMI approach”, Journal of the Korea Society of Ocean Engineers, 17(2), p60-66, (2003), (in Korean).
• U. C. Jeong, S. H. Jeong, and H. W. Chun, “A study on the hull form development and resistance performance of a high-speed coastal patrol boat”, Journal of Ocean Engineering and Technology, 18(3), p44-49, (2004.).
• Y. B. Kim, K. S. Lee, J. H. Kim, and G. H. Chae, “A study on development of an anti-rolling system for the ship stability improvement”, Journal of Korean Society of Marine Environment & Safety, 11(1), p23-28, (2005), (in Korean).
• S. G. Lee, J. M. You, H. H. Lee, S. H. Rhee, and K. P. Rhee, “Experimental study on free roll decay motions of a damaged ship for CFD validation database”, Journal of the Society of Naval Architects of Korea, 45(1), p52-59, (2012), (in Korean). [https://doi.org/10.3744/SNAK.2012.49.1.52]
• D. Y. Jeong, Ship Design, Korea : Myungjin books, (2012), (in Korean).