Proposal for ventilation performance improvement measures considering the ship’s kinetic characteristics in case of hydrogen leakage
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The goal of this research was to propose the shape of a hydrogen fuel storage room according to the roof apex angle considering structural and kinetic characteristics and to analyze the effect of improving ventilation performance accordingly. The computational fluid dynamics (CFD) method was used to analyze the ventilation flow rate of the exhaust vent and average hydrogen concentration value by applying ship motion conditions in the proposed model. Consequently, compared with the flat roof model, the proposed model increased the ventilation flow rate by up to 106% and decreased the hydrogen concentration by up to 28%. Similarly, even in mechanical ventilation, the ventilation flow rate increased by up to 19.02% and the hydrogen concentration decreased by up to 32.97%. The proposed model with a roof apex angle of 120° for both mechanical and natural ventilation was ascertained as the most effective model for hydrogen exhaust. The numerical results are expected to be helpful for research on the design of hydrogen tank storage room shapes and ventilation systems to improve the ventilation performance of hydrogen-powered ships.
Keywords:
Hydrogen leakage, Ventilation, Computational fluid dynamics, Hydrogen fuel storage room1. Introduction
In line with greenhouse gas emission regulations and energy paradigm shifts in shipping and shipbuilding, the need for environmentally friendly and energy-saving ships such as hydrogen ships is increasing [1][2]. Hydrogen fuel is not only eco-friendly, because it does not emit nitrogen oxides (NOx) and sulfur oxides (SOx), but also has advantages such as high energy efficiency and fast charging speed; therefore, it is emerging as a fuel to replace existing ship fuel oil [3][4]. However, the issue of securing safety in using hydrogen as an energy source has been raised due to its low gas density, difficulty in being detected because it is colorless and odorless, and large potential for fuel explosions [5][6]. If hydrogen leaks from the hydrogen tank, hydrogen supply pipeline, and valves due to sealing problems or damage caused by external shocks, the possibility of fire or explosion is high if it cannot be quickly exhausted to the outside [7].
Accordingly, certain research has been conducted on ways to effectively discharge hydrogen when it leaks from a hydrogen ship. Hwang et al. [8] studied the position of the exhaust port to effectively discharge hydrogen when it leaks from the hydrogen tank storage room in a hydrogen fuel cell ship. Their results indicated that the higher the location of the exhaust port, the more effective it was in discharging the remaining hydrogen concentration in the storage room. Hwang et al. [9] conducted a numerical simulation to examine the location and size of the supply port to effectively discharge hydrogen from a hydrogen fuel cell ship. They observed that the smaller the size of the supply port, the more advantageous it was for the rapid hydrogen release. However, they indicated that the higher the position of the air supply port, the higher was the hydrogen concentration by inhibiting the distribution of the air current formed in the space. Lee and Cho [10] analyzed the effect of the area of the supply and exhaust ports on the ventilation performance when hydrogen leaked from a hydrogen tank storage room. They suggested that increasing the area of the inlet port was more effective for hydrogen leakage than increasing the area of the exhaust port. Previous studies have confirmed that to effectively exhaust hydrogen, the location and area of the supply and exhaust ports had to be reviewed when hydrogen leaked from ships.
However, previous studies have identified the following limitations. First, the kinetic characteristics of ships are factors that affect hydrogen diffusion; however, identifying studies evaluating ventilation performance considering these characteristics are difficult. Second, although the shape of the space affects ventilation performance, previous studies did not consider this.
The objective of this study was to propose the shape of the hydrogen fuel storage room based on the roof apex angle to improve the ventilation performance by considering the kinetic characteristics of the ship. Simulated using ANSYS FLUENT 19.2, the study showed the effect of improving the ventilation performance according to the proposed shape and ventilation method.
2. Methodology
Figure 1 illustrates the flowchart of the overall methodology. This included the shape of a hydrogen fuel storage room according to the roof apex angle as a measure to improve the ventilation performance considering the ship’s motion. In addition, the hydrogen dispersion behavior of the proposed model using the ventilation method was analyzed to confirm the effect of improving ventilation performance. Accordingly, the shape of the fuel storage room and optimal ventilation conditions were selected.
2.1 Mathematical model
The simulation was performed using the CFD code FLUENT 19.2 to evaluate the ventilation performance in the proposed model and ventilation method. Hydrogen release and dispersion can be described by the conservation equations of mass, momentum, and energy and the species transport equation, as shown in Equations (1), (2), (3), and (4) [11]. The numerical analysis tool was verified through a previous study [12], and the verification part was not included in this study.
| (1) |
where ρ is the density, t is the time, and is the overall velocity vector.
| (2) |
where p is the pressure, is the stress tensor, is the gravitational acceleration, and is the force vector.
| (3) |
where E is the total energy, keff is the effective conductivity, T is the temperature, hjis the sensible enthalpy of species j, and is the diffusion flux of species j.
| (4) |
where Yi, Ri, and Si is the mass fraction of each species, net rate of the product of species i by chemical reaction, and the rate of creation by addition from the dispersed phase plus any user-defined sources.
2.2 Computational domain
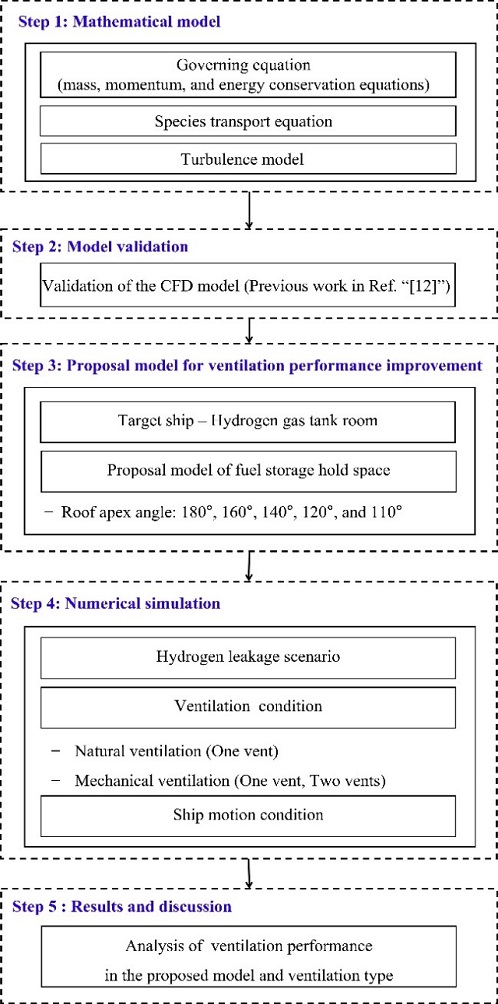
The purpose of this study is to propose the shape of a hydrogen fuel storage room to improve the ventilation performance, and the target model is based on the concept design of a fuel gas supply room (FGSS room) of a hydrogen-powered ship. Hydrogen leakage is highly likely to occur from the hydrogen tank and piping connections, and component equipment other than hydrogen tanks can influence the analysis of the diffusion behavior and act as a variable in shape selection [13]. Therefore, only a hydrogen tank (total internal volume of 21 m3) in a rectangular parallelepipe-shaped (15 m long × 6 m wide × 7 m high) hydrogen fuel storage room was considered for simplification, as shown in Figure 2. The hydrogen tank was assumed to be that of a Type C LNG Tank among the independent fuel tank types stipulated by the IMO, and the detailed specifications are summarized in Table 1 [14].
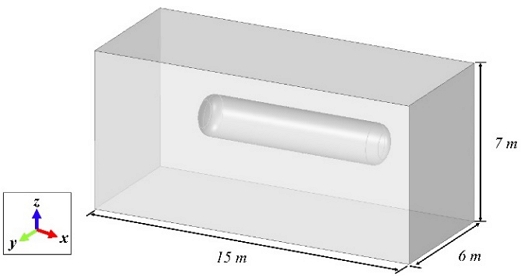
A model was proposed from a structural perspective to improve the ventilation efficiency of a hydrogen gas tank room. According to a study by Perén et al. [15], the roof inclination angle during natural ventilation significantly affected on air flow, and the ventilation volume tended to increase by 22% at 45° compared with that when the roof inclination angle was 0°. Therefore, this study proposed a geometric shape based on the roof apex angle, as shown in Figure 3.
The volume of the model is determined by the cross-sectional area and length of the room, and the cross-section is represented by the side height (h), width (W), roof apex angle (α), and height of the ridge (H). It is divided into the available volume (VA) used to place structural equipment other than hydrogen tanks and the load volume (VL) that acts as a load factor due to ventilation. The effective volume is determined by the height (h) and width, and the load volume is defined as the roof space. In this study, the length (L) and height (H) of the ridge were fixed at 15 m and 7 m, respectively, and the width was adjusted to maintain the same total volume of approximately 630 m3. Table 2 lists the detailed dimensions of the proposed model for the hydrogen tank storage room based on the roof apex angle.
Table 3 summarizes the computing domain, hexahedral grid creation, number of nodes, and orthogonal quality generated for the five different types using ANSYS Meshing. The orthogonal quality is an index that evaluates the quality of a generated grid. The average orthogonal quality for each model was 0.991–0.993, which was within the excellent range [11]. In addition, the numbers of nodes at 180°, 160 °, 140°, 120°, and 110° depending on the roof apex angle were 672,815; 658,060; 663,665; 662,544; and 660,011, respectively.
2.3 Numerical simulation
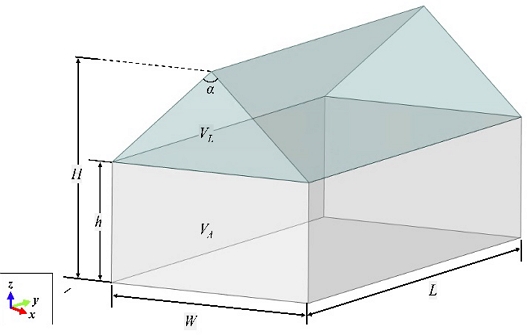
The worst scenario for a hydrogen leakage accident, in which the gas jet leaked from the flange connecting the hydrogen tank and the pipe, was considered in this study. The hydrogen leakage position is shown in Figure 4, and the hydrogen leaks horizontally. The flange size was set to DN250 (applicable pipe inner diameter: 273 mm), and the leak rate was set to 10% of the flange size. In general, high-pressure hydrogen is charged at 35 or 70 MPa; therefore, the pressure of the hydrogen tank was selected based on this. In addition, the hydrogen temperature was selected as 85°C according to the temperature range of 5–85°C, which was selected as the charge/discharge simulation temperature in IS WG24 [16]. To calculate the high-pressure hydrogen leak flow rate, the leakage was determined as either sonic or subsonic. If the tank pressure is higher than the critical pressure calculated according to Equations (5) and (6), the gas is determined to leak at sonic speed, and if the tank pressure is lower than the calculated critical pressure, the gas is determined to leak at subsonic speed. The pressure is 7 × 107 Pa and the temperature is 85 ° C, is calculated as 1.376, and is calculated as 190,333 Pa, and the gas is determined to leak at the speed of sound. The leakage flow rate is calculated according to Equation (7) [17]-[18]. Table 4 presents the hydrogen leakage scenario.
| (5) |
where Pc is the critical pressure, Pa is the atmospheric pressure, and γ is the polytropic index of adiabatic expansion or the ratio of specific heats.
| (6) |
where M is the molar mass, Cp is the specific heat at constant pressure, and R is the universal gas constant.
| (7) |
where Wg is the mass release rate of the gas, Cd is the discharge coefficient, S is the cross section of the opening, P is the pressure inside the container, Z is the compressibility factor, and T is the absolute temperature of the gas.
The ventilation flow rate is 5.25 m3/s when calculated to have a ventilation capacity of at least 30 times per hour according to regulations and 25.93 m/s when converted to speed [19]. Equations (8) and (9) are used to calculate ventilation rates. For natural ventilation, a type 2 ventilation method was applied and evaluated by applying it to the air supply inlet.
| (8) |
where Qvent is the ventilation requirement, Vroom is the volume of the room, and H is the time.
| (9) |
where Voutlet velocity is the ventilation velocity requirement, and Aoutlet is the ventilation area.
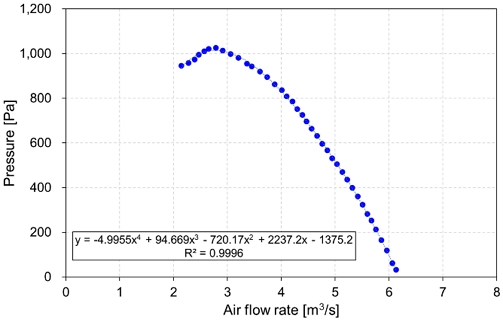
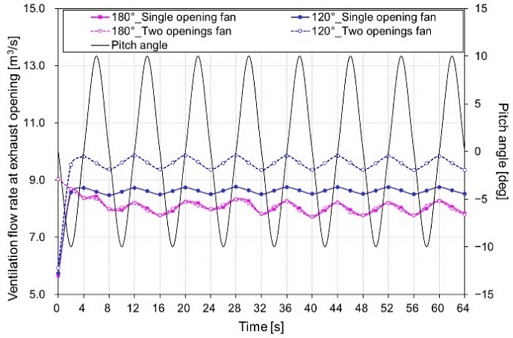
In the case of mechanical ventilation, ventilation is performed using a blower. To consider this in the analysis, the blower characteristic curve was applied to the exhaust opening. Figure 4 shows the characteristic curve of the blower fan prototype that satisfies the required ventilation as a polynomial expression. This was converted into a momentum source and applied in the simulation [20]. The location of the air supply inlet was modeled to be at the bottom of the room, and the exhaust opening was at the top, opposite to the air supply inlet, according to the regulation [21]. When the number of exhaust ports was one, it was placed on the ceiling, opposite to the air supply inlet, and when the number of exhaust openings was two, they were placed on the roof surface of the ceiling.
Previous study confirmed that when the hydrogen leakage is in the longitudinal direction, it is affected by pitch motion [12]. Therefore, pitch motion was applied in the simulation. The motion occurs with an 8-s period according to Equations (10) and (11) [22].
| (10) |
where λ is the pitch angle, and g is the gravitational acceleration.
| (11) |
where fT is the ratio between draught at a loading condition and scantling draught, and L is the overall length.
3. Result and discussion
When a high-pressure hydrogen fuel tank leaks, a large amount of hydrogen (1,976 kg/s) leaks and the gas expands. Thus, when the thickness of the hydrogen gas layer on the ceiling increases and reaches the top of the vent, the gas is discharged outdoors through the vent. Therefore, to evaluate the effect of the ceiling apex angle of the proposed model on hydrogen ventilation, the ventilation flow rate of the exhaust opening and average hydrogen concentration in the room were confirmed.
3.1 Natural ventilation performance of the proposed model
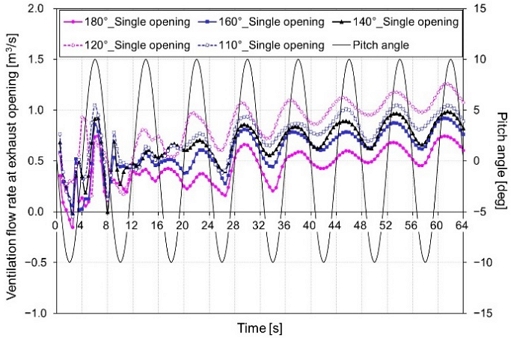
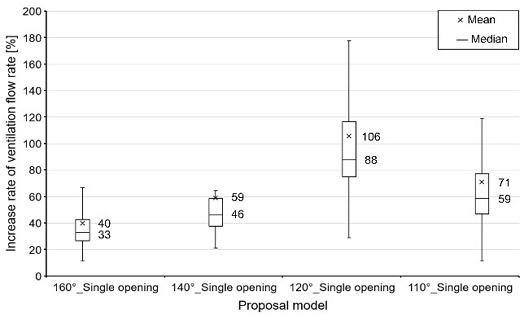
Figure 5 shows the ventilation flow rate at the exhaust opening based on the roof apex angle. As the roof apex angle decreased to 120 °, the ventilation flow rate increased, and the tendency to repeat the rise and fall according to the period could be confirmed. In particular, the largest difference occurred when the pitch angle at 34 s was -10°. When the apex angle was 180°, the ventilation flow rate was 0.21㎥/s, whereas when the apex angle was 160°, 140°, 120°, and 110°, the ventilation flow rate was 0.44㎥/s, 0.58㎥/s, 0.78㎥/s, and 0.68㎥/s, respectively, indicating an increase of 114.5%,177.8%, 275.6%, and 226.9%, respectively. The rate of increase in ventilation flow compared with that at 180 ° is shown in Figure 6 as a box plot graph. Although a large variation occurred in ventilation due to changes in exercise, the average ventilation increased by 40%, 59%, 106%, and 71% at 160 °, 140°, 120°, and 110°, respectively, compared with that at 180°. Thus, even if the air supply was the same, a ventilation plan considering this was necessary because the difference in exhaust occurs depending on the motion period and shape of the space.
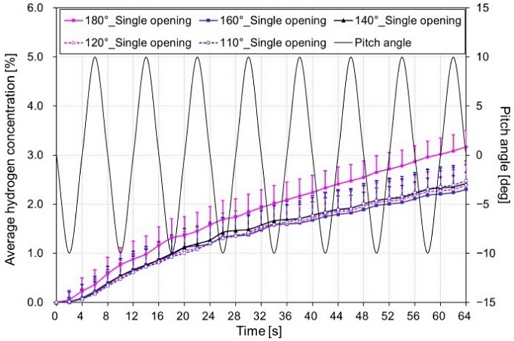
The average concentration of the hydrogen remaining in the room for each proposed model is shown in Figure 7. In addition, the decrease rate of hydrogen concentration compared with that at 180° is shown in Figure 8 as a box plot graph. Overall, the average hydrogen concentration tended to be lower as the roof apex angle decreased, but no significant difference existed between 25 and 28% for each angle compared with that for 180°. This result is due to the failure to provide sufficient ventilation compared with the amount of hydrogen leakage. Therefore, mechanical ventilation method was applied, and the number of exhaust ports was added to confirm the ventilation performance.
3.2 Mechanical ventilation performance of the proposed model
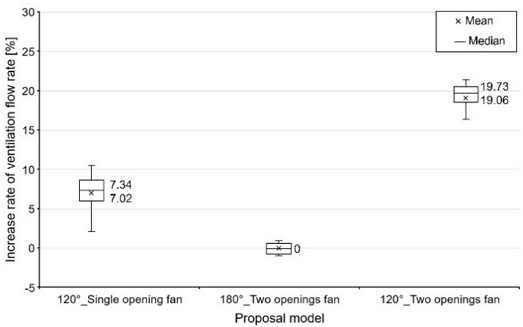
The hydrogen leakage according to the ventilation conditions was analyzed by setting the roof apex angle to 120°, which is the most effective model for hydrogen exhaust during natural ventilation, as an experimental group and a roof apex angle of 180° as a control group. Figure 9 shows the ventilation flow rate at the exhaust opening due to the installation of the blower, and Figure 10 shows the increase rate of the ventilation flow rate by the number of exhaust openings in a box plot graph. Unlike natural ventilation (type 2 ventilation), mechanical ventilation (type 1 ventilation) had a constant ventilation volume. In addition, when the roof apex angle was 180 °, no difference existed in the amount of ventilation despite the increase in the number of exhaust openings. This implied that a stagnant area existed during hydrogen leakage; therefore, the effect of the number of exhaust openings and the blower was small. However, when the roof apex angle was 120 °, ventilation flow increased by at least 10% to a maximum of 13% with two openings compared to one. This implied that when hydrogen leaked, it accumulated on the roof side of the zone and was discharged through openings located on the roof side. In terms of ventilation, compared with a 180° single opening fan, the average increase was 7.02% for a 120° single opening fan and 19.02% for a 120° two openings fan. This confirmed that the amount of ventilation increased at 120°.
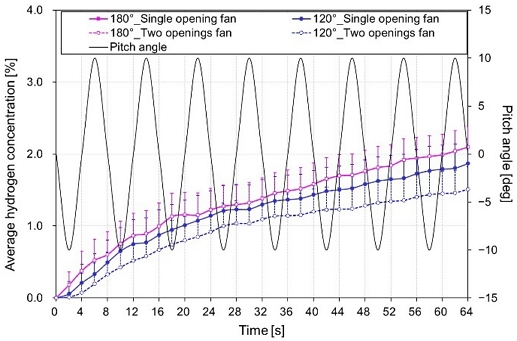
The average hydrogen concentration remaining in the room according to the ceiling apex angle and number of exhaust openings are shown in Figure 11. In addition, the reduction rate of hydrogen concentration compared with that at 180 ° is shown in Figure 12 as a box plot graph. When the roof apex angle was 180 °, although the number of exhaust outlets increased, no difference was observed in hydrogen concentration because the amount of ventilation was the same. In addition, when the ceiling apex angle was 120 °, the hydrogen concentration decreased by a minimum of 16% to a maximum of 25% with two openings compared with that with a single opening. This can be attributed to the increase in ventilation due to the increase in the number of openings. The hydrogen concentration compared with that at the 180° single opening was reduced by an average of 13.98% in the case of a 120° single opening fan and 32.97% in the case of a 120° two openings fan. Thus, the hydrogen concentration value decreased due to the increase in ventilation when both natural and mechanical ventilation were at 120 °.
4. Conclusion
The purpose of this study was to propose a shape and ventilation method for a hydrogen fuel storage area considering the structural and environmental characteristics of the ship to effectively discharge hydrogen during leakage and analyze the effect of improving ventilation performance. The results obtained in this study are summarized as follows:
- 1) Ventilation performance was compared according to the apex angle (160°, 140°, 120°, and 110°) of the ceiling of the hydrogen fuel storage room when natural ventilation was applied. The ventilation flow rate increased up to 106% (120°) depending on the ceiling angle, and hydrogen concentration decreased up to 28% (120°).
- 2) When mechanical ventilation was applied, hydrogen leakage analysis was performed on the model (120°), which is the most effective for hydrogen emission in natural ventilation and a ceiling apex angle of 180° (control group), and the ventilation flow rate and hydrogen concentration values were compared. As a result, the ventilation flow rate increased by up to 19.02%, and the hydrogen concentration decreased by up to 32.97%.
In summary, considering the characteristics of the ship, the ventilation performance was most effective when ceiling apex angle of the hydrogen fuel storage space was 120 °. However, when applying hydrogen leakage and ventilation scenarios, research on the quantification of hydrogen diffusion characteristics according to leakage and ventilation characteristics must be conducted by applying various conditions, such as the size of the leak port, leak amount, leak direction, and size of the ventilation port. These considerations can overcome the limitations of the application of various ship ventilation conditions.
Author Contributions
Conceptualization, B. Kim and K. I. Hwang; Methodology, B. Kim; Software, B. Kim; Formal Analysis, B. Kim and K. I. Hwang; Investigation, B. Kim; Resources, B. Kim; Data Curation, B. Kim; Writing—Original Draft Preparation, B. Kim; Writing—Review & Editing, B. Kim and K. I. Hwang; Visualization, B. Kim; Supervision, K. I. Hwang; Project Administration, K. I. Hwang; Funding Acquisition, K. I. Hwang.
References
- International Maritime Organization (IMO), Initial IMO Strategy on Reduction of GHG Emissions from Ships, Resolution MEPC.304(72), 2018.
-
O. B. Inal, B. Zincir, and C. Dere, “Hydrogen as maritime transportation fuel: A pathway for decarbonization,” Greener and Scalable E-fuels for Decarbonization of Transport, pp. 67-110, 2021.
[https://doi.org/10.1007/978-981-16-8344-2_4]

- I. Mun, E. -J. Kim, and K. -H. Lee, Introduction to Hydrogen Safety, 1st edition, Seoul, Korea: Chungsong Media, 2019.
-
G. Cipriani, V. Di Dio, F. Genduso, D. La Cascia, R. Liga, R. Miceli, and G. R. Galluzzo, “Perspective on hydrogen energy carrier and its automotive applications,” International Journal of Hydrogen Energy, vol. 39, no. 16, pp. 8482-8494, 2014.
[https://doi.org/10.1016/j.ijhydene.2014.03.174]

-
D. A. Crowl and Y. -D. Jo, “The hazards and risks of hydrogen,” Journal of Loss Prevention in the Process Industries, vol. 20, no. 2, pp. 158-164, 2007.
[https://doi.org/10.1016/j.jlp.2007.02.002]

-
F. Rigas and P Amyotte, Hydrogen safety, 1st ed, Boca Raton, United States: CRC Press, 2012.
[https://doi.org/10.1201/b12267]

-
F. Li, Y. Yuan, X. Yan, R. Malekian, and Z. Li, “A study on a numerical simulation of the leakage and diffusion of hydrogen in a fuel cell ship,” Renewable and Sustainable Energy Reviews, vol. 97, pp. 177-185, 2018.
[https://doi.org/10.1016/j.rser.2018.08.034]

-
D. -J. Hwang, B. -L. Kil, S. -K. Park, and M. -H. Kim, “Numerical study on the location of exhaust outlet for effective ventilation in the event of hydrogen gas leakage in a hydrogen tank storeroom,” Journal of the Korean Society of Marine Engineering, vol. 41, no. 7, pp. 619-625, 2017 (in Korean).
[https://doi.org/10.5916/jkosme.2017.41.7.619]

-
D. -J. Hwang, B. -L. Kil, S. -K. Park, and M. -H. Kim, “Numerical study on the effect of location and size of air intake inlet for effective ventilation in a hydrogen tank storeroom,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 3, pp. 142-147, 2018 (in Korean).
[https://doi.org/10.5916/jkosme.2018.42.3.142]

-
C. -Y. Lee and D. -H. Cho, “Numerical study on the effect of area changes in air inlets and vent ports on the ventilation of leaking hydrogen,” Journal of the Korean Society of Marine Environment & Safety, vol. 28, no. 2, pp. 385-393, 2022.
[https://doi.org/10.7837/kosomes.2022.28.2.385]

- ANSYS, ANSYS Fluent Theory Guide, Release 19.2, Canonsburg, United States, 2019.
-
B. Kim, K.-I. Hwang, “Numerical analysis of the effects of ship motion on hydrogen release and dispersion in an enclosed area,” Applied Sciences, vol. 12, no. 3, p. 1259, 2022.
[https://doi.org/10.3390/app12031259]

-
B. D. Ehrhart, E. S. Hecht, and K. Groth, Hydrogen Risk Assessment Models(HyRAM) Version 3.0 Technical Reference Manual, Sandia National Lab., United States, 2020.
[https://doi.org/10.2172/1673177]

- S. -H. Cho, M. -J. Sim, Y. -J. Jung, and I. -S. Kim, “A study on thermal performance evaluation procedures of LNG fuel tank,” Journal of the Korean Institute of Gas, vol. 22, no. 3, pp. 45-52, 2018 (in Korean).
-
J. I. Peren, T. van Hooff, B. C. C. Leite, and B. Blocken, “CFD analysis of cross-ventilation of a generic isolated building with asymmetric opening positions: Impact of roof angle and opening location,” Building and Environment, vol. 85, pp. 263-276, 2015.
[https://doi.org/10.1016/j.buildenv.2014.12.007]

- ISO “Gaseous Hydrogen – Fueling Protocols for Hydrogen-Fuelled Vehicles”, ISO/TC 197/WG24, 2020.
- Korea Occupational Safety and Health Agency, Technical guidance on source term modeling, Ulsan, Korea, 2012.
- Korea Occupational Safety and Health Agency, Technical guidance on accident damage prediction techniques, Ulsan, Korea, 2021.
- Ministry of Oceans and Fisheries, Code of Safety for Ships Using Gases or Other Low-Flashpoint Fuels, 2020 (in Korean). [Online]. Available: https://law.go.kr/LSW/admRulLsInfoP.do?admRulSeq=2100210000019, .
- GS Fan, Technical data for fan, http://www.gsfan.co.kr/view/technical.html, , Accessed December 4, 2022.
- Korean Register, Guideline of marine fuel cell system, 2022 (in Korean). [Online]. Available: https://www.krs.co.kr/KRRules/KRRules2022/data/data_othot/korean/gc12k000.pdf, .
- Det Norske Veritas group, Rules for classification: Ships-DNVGL-RU-SHIP-Pt3Ch4, 2015.