Development of energy management system using neural network for power electric system
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
With the international community's efforts to reduce carbon dioxide, the technology to improve the energy efficiency of ships has been significantly advanced owing to the development of propulsion and power systems. Among them, the power management system in the electric propulsion system, which is a eco-friendly technology, has been transformed to an energy management system(EMS) that integrates the battery management system or green technologies to improve system efficiency. The application of EMS can improve the efficiency of the power system by applying this technology not only to the electric propulsion system but also to the power generation system in merchant ships using the conventional direct mechanical propulsion system. Optimum control of the power generation source according to the rule-based strategy, including the load and state of charge of the battery, referring to the designer's intentions, is presented in this study. The neural network controller logic is developed, and the stability of the control system is analyzed using Matlab/Simulink based on various environments. As a test result, according to the step-by-step changes in load and battery status, the designed learning value shows a stable generator output command value in all operation areas and a stable generator optimal control output according to various conditions.
Keywords:
Rule based strategy, Neural network, Power management system, Energy management system, Optimum control1. Introduction
The international community has strengthened regulations on emissions from ships, and the IMO(International Maritime Organization) has tightened regulations on air pollution emitted from ships [1]. Accordingly, various alternatives such as EEDI(Energy Efficiency Design Index) power system improvement, low-carbon fuel, etc. have been proposed to reduce carbon dioxide [2], and the engine system is also being improved as a solution [3]. This affects not only the change of the propulsion system, but also the improve the efficiency of the power system. In the power system, the conventional parallel running load-sharing power generation system has limitations such as frequent maintenance cycle, increased emissions due to the fuel consumption increase by the low efficiency of the power source in the case of low-load operation [4]. To improve this, various fuels for engines, types of sources, and efficiency improvement measures for power generation sources have been introduced [5][6]. Among them, a hybrid power system using a battery system can also be a solution to improve system efficiency [7]. The efficiency of the system can be improved by the optimal operation of the power source and the battery system’s compensation. Comprehensive control of the battery management system linked with the existing power management system can be managed by the EMS(Energy Management System) [8]; the EMS controller is devised and used by various control methods [9]. In this study, by applying a rule-based strategy, the operation mode of the power generation system according to the load condition and battery SOC and the operation command for each generator were set. In addition, the EMS control results considering the SOC of the battery as a power source and the system without considering the SOC’s effects on the results of the EMS controller were also examined through simulation. To improve the efficiency of the system, the optimal operation point of the power source is designed to be operated in as many sections as possible, and the battery system is designed to compensate for variable load conditions.
2. Power management system and energy management system for ship
2.1 Conventional Power Management System
In the case of load sharing in the conventional electric power system of a ship, the output of the power generation load operated according to the time-varying load condition, as shown in Equation (1). It is equal to the value obtained by dividing the total power load required by the number of operating power sources. It is operated in parallel or in a programmed setting as some generators operate in the optimal operation mode and other power sources are allowed to handle the rest of the demanding load.
| (1) |
In this case, the efficiency of the entire power generation source decreases during equivalent parallel operation, which leads to low system efficiency; this causes an increase in carbon dioxide emissions due to an increase in fuel consumption [4]. Even in the case of some optimal operation mode, it is difficult to evaluate whether the efficiency of the entire system has been improved to a satisfactory level because the efficiency of the low-load power generation source operated asymmetrically is low. When the battery SOC is not considered as reserve power, system maintains the SOC level of the battery properly, but when the battery SOC is considered, the battery SOC will be completely consumed after a specific operation time. The load balancing of the system with the battery is represented in Equation (2)
| (2) |
2.2 Control Strategy of Energy Management System not Considering Battery SOC
As shown in Table 1, if the battery SOC is not considered a reserve power source, it operates in five operating modes. The generator's operation command is designed to be taken as G_STOP, G_OPT, α = PLOAD + PG_min is set in consideration of the minimum generator operation output value in the design standard of the load standard to designate the initial battery charge and the charging section of the battery according to the section without considering the battery SOC as a reserve power. The output command rule for each source was created.
2.3 Control Strategy of Energy Management System Considering Battery SOC
When the battery is considered as the reserve power of the load, the overall generator output command value is reduced because the system power is compensated by the battery. As shown in Table 2, unlike Table 1, by setting β = PLOAD − PBATt, a different operation mode is obtained according to the load condition category. The generator operation status is set to G_STOP, G_VAR, G_OPT.
3. Design of energy management system using neural network
3.1 Specification and test environment
To design the controller for EMS according to the designed rule, the system capacity (system load, generator engine, and battery) was selected as shown in Table 3, and the NCR output of the generator engine was selected as 2,000 kW considering the engine margin. All the design specifications were calculated to control the generator engine’s output, as shown in Table 4.
3.2 Training data for neural network
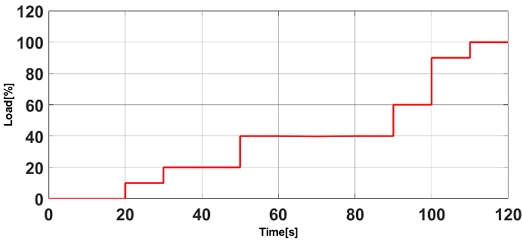
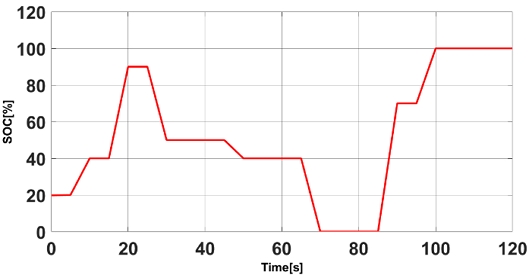
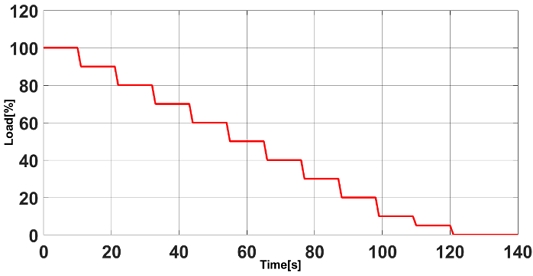
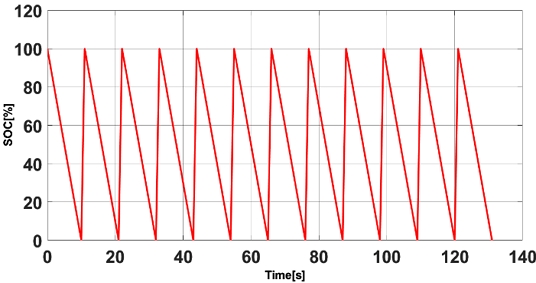
To test the responsiveness and stability of the generator output command controller of the system according to the time-varying load and SOC variation, the environment shown in Figures 1 and 2 was selected as the final experimental environment.
Table 5 shows the neural network training values that do not consider the battery SOC as a reserve power based on the rule-based strategy for the generator output command according to the ship’s load and the battery SOC value in consideration of the simulation environment. Table 6 shows the neural network learning values considering the SOC value.
The gray section indicates the operation where the battery is no longer charged from the system when the battery SOC value reaches 90% or more, and PG_min is set to 0 at α = PLOAD + PG_min and trained.
3.3 Neural network application
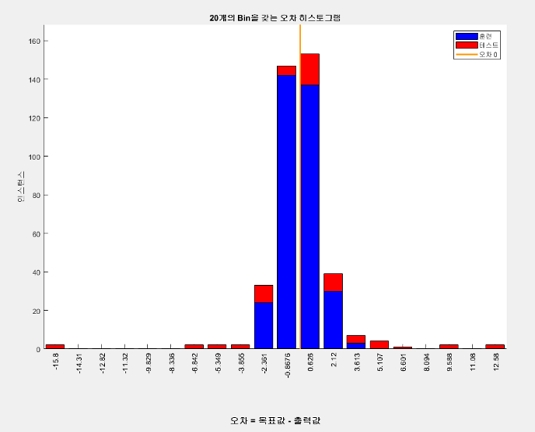
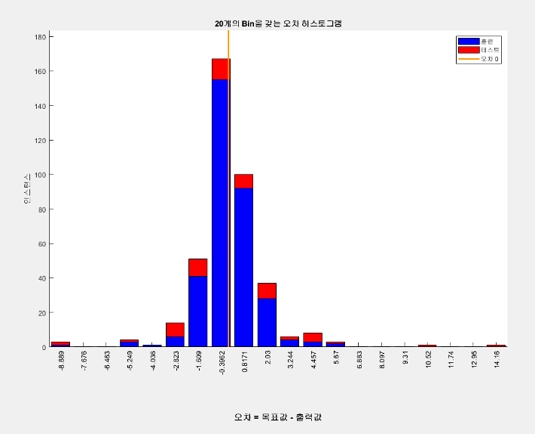
The designed neural network controller had a single-layer neural network; the hidden layers were composed of 30 layers; and a neural network controller using Bayesian regularization was applied. As shown in Figures 3 and 4, the error in the output value of the learned neural network controller can be compensated by the battery system, so it does not affect the output or operation performance.
3.4 Training result by neural network controller
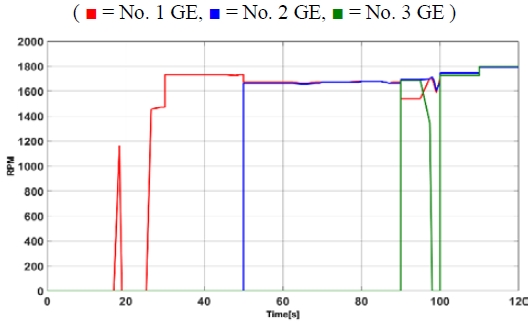
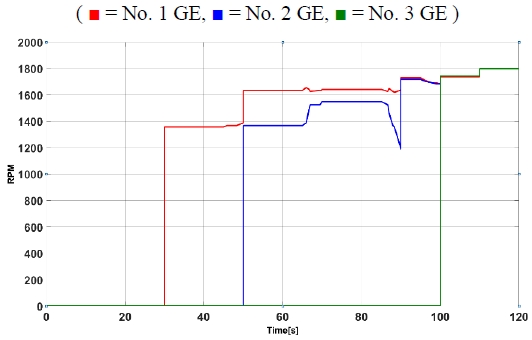
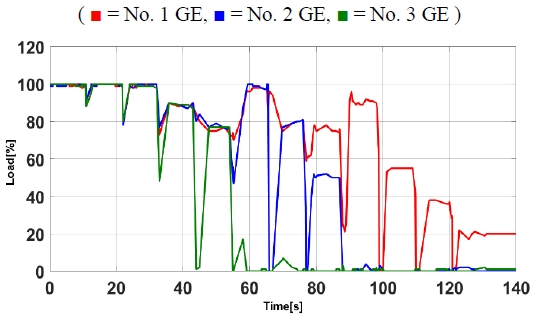
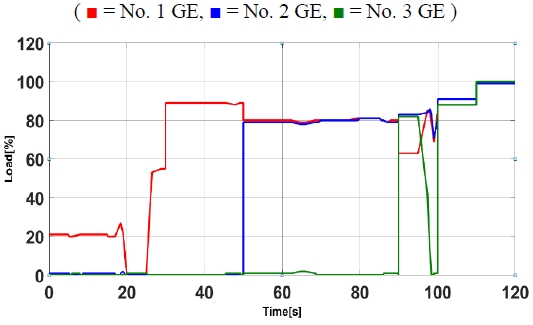
In addition, to verify the control stability of the designed neural network, the load and battery SOC values as shown in Figures 5 and 6 that were used for learning were applied to verify that the generator output command value matches the learned value and to confirm that there are no irregular or uncontrollable areas in the control result. Figures 7 and 8 depicts the results, which are stable.
Result of neural network controller output tested in step load and step battery SOC not considering battery SOC
3.5 Simulation
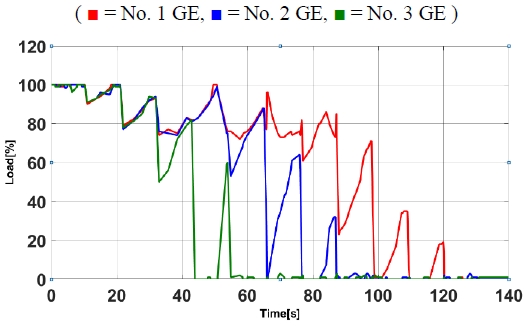
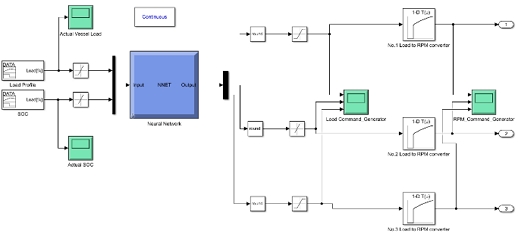
The system shown in Figure 9 was designed through Matlab/Simulink to apply the unspecified ship power load and battery SOC value as input values using the verified neural network controller to make the output command value for the generator output through the controller which prove the stability of the controller.
As shown in Figures 10 and 11, if the battery SOC is not considered, the required output of the power source is higher. However, as a result of both designs, the power generation source was designed to have a parallel operation form above a certain load exceeding the optimum operation output value of the power source.
Result of neural network controller output tested in specific load and battery SOC not considering battery SOC
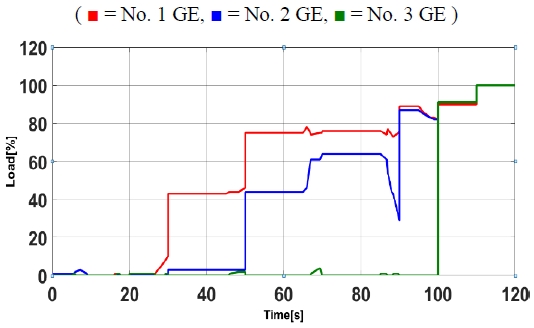
Result of neural network controller output tested in specific load and battery SOC considering battery SOC
As shown in Figures 12 and 13, the command value converted from the generator output command value using the load-RPM table designed in Table 4. It is for a command as the generator angular speed command. It was confirmed that irregular values or oscillation situations did not occur.
4. Conclusion
Through this study, our novel research made the following contributions and findings.
- 1) It was simulated through Matlab/Simulink to design a neural network controller that contributes to the improvement of system efficiency by applying an EMS that manages the battery hybrid system to the power system of a general merchant ship.
- 2) The error between the designed rule-based control value and the neural network controller output was minimized using the Bayesian regularization technique.
- 3) In the controller design, the output of the neural network controller according to the time-varying load is set by setting the optimal operation command of the power source according to the designer's intention and comparing the case where the battery SOC is considered a reserve power source with the case where the battery SOC is not considered under the same load condition.
- 4) It was confirmed that the control characteristics of the command value were stable in designed load and SOC conditions and in a specific test environment too.
However, for future study, the speed range of the engine should be considered for generator control in consideration of the lubricating and mechanical characteristics of the engine.
Acknowledgments
This work was supported by the Technology development program(P0016077) funded by the Ministry of SMEs and Startups(MSS, Korea).
Author Contributions
Conceptualization, S. W. Kim; Methodology, S. W. Kim; Software, S. W. Kim and S. C. Kang; Formal Analysis, M. K. Son and S. C. Kang; Investigation, H. M. Jeon and S. C. Kang; Resources, H. M. Jeon; Data Curation, M. K. Son and S. C. Kang; Writing-Original Draft Preparation, S. W. Kim; Writing-Review & Editing, H. M. Jeon; Visualization, M. K. Son and S. C. Kang; Supervision, S. W. Kim and H. M. Jeon; Project Administration, H. M. Jeon; Funding Acquisition, H. M. Jeon.
References
-
T. C. Van, et al., “Global impacts of recent IMO regulations on marine fuel oil refining processes and ship emissions,” Transportation Research Part D: Transport and Environment, vol. 70, pp. 123-134, 2019.
[https://doi.org/10.1016/j.trd.2019.04.001]

-
E. A. Bouman, et al., “State-of-the-art technologies, measures, and potential for reducing GHG emissions from shipping – A review,” Transportation Research Part D: Transport and Environment, vol. 52, Part A, pp. 408-421, 2017.
[https://doi.org/10.1016/j.trd.2017.03.022]

-
T. -H. Joung, et al., “The IMO initial strategy for reducing Greenhouse Gas (GHG) emissions, and its follow-up actions towards 2050,” Journal of International Maritime Safety, Environmental Affairs, and Shipping, vol. 4, no. 1, pp. 1-7, 2020.
[https://doi.org/10.1080/25725084.2019.1707938]

-
M. Jaurola, et al., “Optimising design and power management in energy-efficient marine vessel power systems: a literature review,” Journal of Marine Engineering & Technology, vol. 18, no. 2, pp. 92-101, 2019.
[https://doi.org/10.1080/20464177.2018.1505584]

-
V. C. Pham, et al., “Effects of various fuels on combustion and emission characteristics of a four-stroke dual-fuel marine engine,” Journal of Marine Science and Engineering, vol. 9, no. 10, p. 1072, 2021.
[https://doi.org/10.3390/jmse9101072]

-
C. W. Noor, M. M. Noor, and R. Mamat, “Biodiesel as alternative fuel for marine diesel engine applications: A review,” Renewable and sustainable energy reviews, vol. 94, pp. 127-142, 2018.
[https://doi.org/10.1016/j.rser.2018.05.031]

-
R. Barrera-Cardenas, O. Mo, and G. Guidi. “Optimal sizing of battery energy storage systems for hybrid marine power systems,” 2019 IEEE Electric Ship Technologies Symposium (ESTS), pp. 293-302, 2019.
[https://doi.org/10.1109/ESTS.2019.8847932]

-
J. Han, J. -F. Charpentier, and T. Tang, “An energy management system of a fuel cell/battery hybrid boat,” Energies, vol. 7, no. 5, pp. 2799-2820, 2014.
[https://doi.org/10.3390/en7052799]

-
S. Kim and J. Kim, “Optimal energy control of battery hybrid system for marine vessels by applying neural network based on equivalent consumption minimization strategy,” Journal of Marine Science and Engineering, vol. 9, no. 11, p. 1228, 2021.
[https://doi.org/10.3390/jmse9111228]