Resonant power transmission through a ridged circular aperture with variable aperture dimensions and its arrays

1. Introduction

The electromagnetic resonant coupling problem, which occurs when electromagnetic waves are transmitted through electrically small apertures or holes, has been well-researched for decades, as it is of interest to many researchers in the fields of optics and microwaves. This problem was first posed by Bethe [1] and was solved mathematically in a strict manner. According to the theory proposed by Bethe, the transmission characteristics are proportional to (a/λ)⁴, where a is the radius of the circular hole and λ is the wavelength. The transmitted power is extremely low for small apertures; in other words, the transmission efficiency is poor. After several decades, the concept of an equivalent circuit was introduced to better study resonant phenomena in circular apertures, and the term “radiation resistance” was posited to generalize this problem [2]. According to this theory, if the resonance condition is properly satisfied, there may be room for improvement in transmission characteristics. The resonance condition is established by adding a capacitor component to the small aperture. Through this approach, electromagnetic transmission can be maximized.

Since 2000, many researchers in the optical field have conducted studies on nanosized optical probes to observe resonant transmission changes as a function of aperture shape; Their studies have revealed that it is possible to maximize the transmission phenomenon. Consequently, these findings can be applied to optical applications, such as nano-microscopy, nanolithography, and optical data storage [3]-[6].

Some typical examples of adding capacitive structures to single circular apertures are as follows. First, it was revealed that a capacitor component was imparted by adding a ridge parallel to the electric field component of the incident wave at the circular aperture; thus, the transmission phenomenon was maximized at frequencies lower than that of the original circular aperture. These results were verified using two numerical techniques and compared. In contrast to that of a conventional circular aperture without ridges, the transmission of the ridged circular aperture (RCA) was better maximized at a lower frequency [7]. Second, when RCAs are arranged side by side and collinearly, the resonant transmission characteristics as a function of the distance between the two RCAs can also be revealed. By observing the change in the transmission characteristics according to distance, it is possible to derive the transmission principle at greater depths than the antenna gain according to the distance between the two dipole antennas [8]. By extending this study, an equivalent circuit model was proposed, and the admittances of the aperture from the transmission resonance phenomenon for a single RCA were systematically analyzed [9].

In this study, we intend to expand on previous studies and examine how the resonant transmission characteristics change as the shape of the ridge in the RCA changes. Specifically, we examine how changes in the resonance frequency are observed as functions of the width of the ridges and gap between the two ridges. In addition, we examine how the transmission characteristics change when the ridge orientations between the two RCAs are arranged side by side or collinearly. Through such a series of analyses, it is possible to understand the resonant transmission of electromagnetic waves through a single RCA and determine the applicability of RCA miniaturization to various fields of research.

2. Problem geometry and resonant transmission

Figure 1 shows a schematic of the RCAs perforated on a thin perfect electric conductor (PEC) screen, where the circular radius D/2 is 3.75 mm, spacing (gap) g between the two ridges is 0.9 mm, and width of the ridges w is 2.1 mm. An electromagnetic plane wave is incident along the z-axis from the rear half-infinite plane (z < 0) to the front half-infinite plane (z > 0). Here, the incident electric field is polarized in the y direction, which is the same as the ridge direction. In a previous study [7], cases were compared where the ridge was not included and the polarization was on the x-axis. Therefore, it was confirmed that higher transmittance was observed in this case, as shown in Figure 1.

Figure 1:

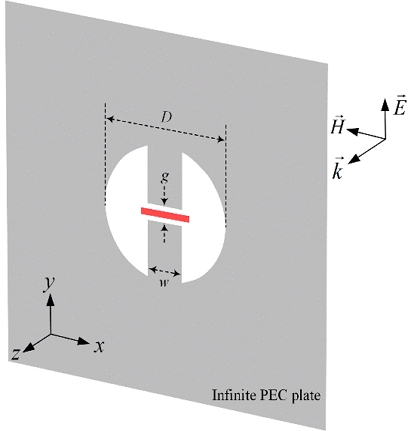
Single-ridged circular aperture perforated on a thin infinite perfect electric conductor screen. The aperture’s variables are described, and the plane’s electromagnetic wave is incident along the +z direction. The concentrated incident electric field is described in red along the x-axis and can be transformed into an equivalent magnetic current element.

There are various numerical techniques for analyzing the structure in Figure 1. However, the 3-dimensional (3D) finite-difference time-domain (FDTD) method is relatively easy to apply and is useful for deriving resonant transmission results. The unit cells along the x-axis, y-axis, and z-axis are 0.15 mm each. A perfectly matched layer absorbing boundary condition is applied at all six boundaries. From Maxwell’s equation, the unit time step was obtained as 2.60 × 10^–13 s, which was determined by the Courant factor and stability condition in the general FDTD algorithm [10]. A Gaussian waveform was applied in the form of an incident wave and was obtained as exp{–(t – t₀)²/τ²}, where τ was 5.003 ps, and t₀ was usually taken as 4.5τ [10]. This fundamental analytical technique and the values are applicable to arrayed RCAs as well as to other single RCA shapes.

A transmission cross section (TCS) can be obtained from the result of the FDTD computational simulation, which is a criterion used to calculate the transmission efficiency through a small hole. TCS is defined as the ratio of the transmitted power P_trans to the incident power density P_inc as follows:

where $$ {\overrightarrow{E}}_t$$ and $$ {\overrightarrow{H}}_t$$ are the transverse electric and magnetic fields on the aperture, respectively, asterisk ^* indicates the complex conjugate, and $$ d\overrightarrow{s}$$ is the unit square cell area of the aperture. The incident power density is calculated from $$ P_{\text{inc}}={\left|{\overrightarrow{E}}_{inc}\right|}^2/\left(2{\eta }_0\right)$$, where $$ {\overrightarrow{E}}_{inc}$$ is the electric field intensity of the incident plane wave with a Gaussian form, and η₀ (=120π) is the intrinsic impedance of free space. From the definition, the TCS for the single RCA shown in Figure 1 is calculated as approximately 181 mm² at a resonant frequency of 11 GHz when g = 0.9 mm and w = 2.1 mm. This value is almost the same as 3λ²/(4π) m² [11], which is the theoretically confirmed value. Therefore, the value obtained by the above FDTD method is verified as valid. On the other hand, the maximum TCS of 74.78 mm² was calculated at a resonant frequency of 20.12 GHz, when the ridges were not considered and the diameter was kept at 7.5 mm as well. Meanwhile, TCS was obtained as 10.82 mm² at 11.02 GHz. Therefore, it can be seen that the TCS is improved by approximately 17 times at 11.02 GHz when the ridges are included. From another point of view, it can be applied for the miniaturization of aperture antennas because the resonant frequency decreases.

The incident electric field was excited along the y-axis between the two ridges. However, the electric field was concentrated along the gap width w at a narrow gap spacing g. Therefore, it is said that the electric field was focused along the x-axis. This is the same as the red line in Figure 1. Additionally, the fact that the red line is longer than the ridge width w indicates the presence of the fringing effect.

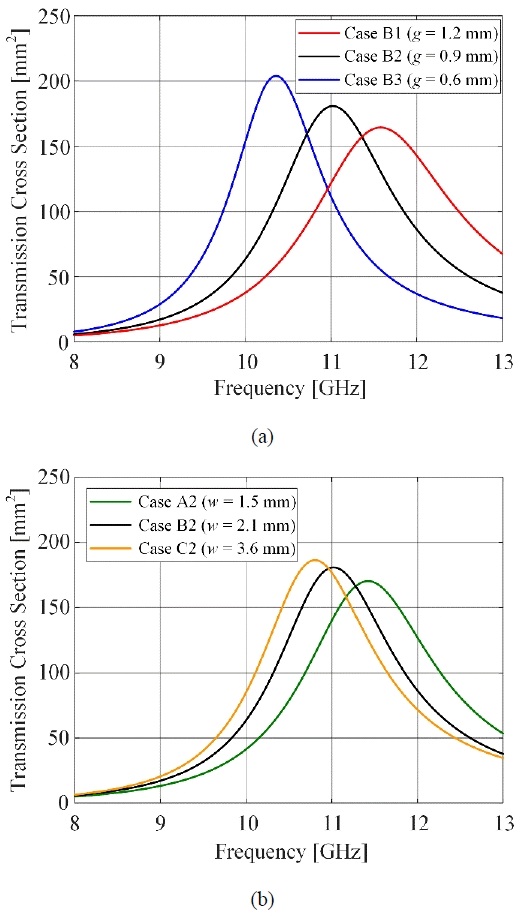
Figure 2 shows the five types of RCAs that were analyzed. The middle RCA (Case B2) among the five apertures was the structure that was examined as the starting point, as explained in the previous section. The gap between the ridges g was 0.9 mm, and the width of the ridges w was 2.1 mm. Then, the aperture where the width of ridge w narrowed (widened) was located on the left (right) of Case B2. This case was referred to as Case A2 (Case C2). Meanwhile, the gap between the upper and lower ridges was the same as that in Case B2. The widths of the ridges were 1.5 mm and 3.6 mm for Cases A2 and C2, respectively. Next, the other two RCA changes (above and below Case B2 in Figure 2) involved alterations in the distance between the two ridges. In Case B2, the gap spacing was kept at 0.9 mm, while Case B1 had a wider gap of 1.2 mm, and Case B3 had a narrower gap of 0.6 mm. Similarly, the ridge width w was kept at 2.1 mm for Cases B1 and B3. Thus, it was possible to observe the changes in the transmission characteristics caused by the shape changes in the five RCAs.

Figure 2:

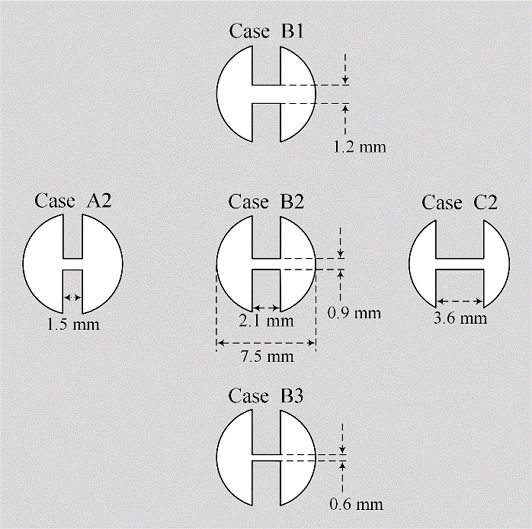
Five RCA cases are shown as functions of the ridge width w and gap g between the two ridges. The TCSs were tested for each RCA case.

Figure 3 shows the TCSs according to the changes in aperture shapes, as shown in Figure 2. As can be seen in Figure 3(a), the resonant frequency changes as the gap between the two ridges g varies, and the corresponding maximum TCSs also change. As stated in the introduction, the inductance component of the circular aperture itself is dominant; therefore, if the upper and lower ridges are added, the capacitance component is added, and the resonance phenomenon starts to occur. Since the capacitance increases as the gap g decreases, on the one hand, the resonance frequency decreases according to the relationship whereby the resonance frequency is proportional to $$ 1/\sqrt{LC}$$ ; this tendency can be confirmed, and is shown in Case B3 of Figure 3(a). On the other hand, as gap g increases, the concentrated electric field intensity weakens, the corresponding capacitance decreases, and the resonant frequency increases. The TCSs for Cases B1, B2, and B3 were calculated as 203.97, 180.84, and 164.40 mm² at resonant frequencies of 10.36, 11.02, and 11.58 GHz, respectively.

Figure 3:

Transmission cross sections as a function of frequency for the cases in Figure 2.

Figure 3(b) shows the transmission characteristic variations as the width w of the upper and lower ridges changes. Similar to Figure 3(a), Case B2 in Figure 2 is again the basic structure. When the ridge width w was reduced to 1.5 mm, as in Case A2, the induced incident electric field diminished, and the corresponding capacitance was also reduced. Therefore, according to the relationship between the resonant frequency, inductance, and capacitance, the resonant frequency increases, and the corresponding TCS decreases. On the other hand, when the width w increases to 3.6 mm in Case C2, the concentrated incident electric field is widely developed and, at the same time, the resulting capacitance increases. Accordingly, the resonant frequency decreases, whereas the corresponding TCS increases.

From Figure 3, it is understood that the capacitances change as the ridge shapes change; consequently, the resonant frequencies and TCSs vary. Although there are few examples, it is confirmed that changes in the ridge gap have a greater impact on the resonance than variations in the ridge width. This means that the concentration of the incident electric field is more affected by the gap g than by the width w.

From Figure 3, the theoretical maximum TCSs and numerically calculated maximum TCSs at the resonant frequencies can be summarized and compared, as listed in Tables 1 and 2. The transmission characteristics of the resonant aperture were theoretically derived and corresponded to 3λ²/(4π) [11], which were very similar to the calculated TCSs.

Table 1:

TCS comparison between computational and theoretical TCSs when the gap between two ridges g varies (from Figure 3(a)).

Table 2:

TCS comparison between computational and theoretical TCSs when the ridge width w varies (from Figure 3(b)).

The geometric parameters g and w in Figure 1 are relatively small compared with the wavelength of the resonant frequency. The circular aperture alone is dominated by an inductive component; however, a resonant effect is obtained at a lower frequency by adding upper and lower ridges, which could be interpreted as the capacitive component. Therefore, it can be useful for the miniaturization of aperture antennas and frequency-selective surface design. Furthermore, this study focused on the analysis at 11 GHz. If the geometric scales are proportionally changed (greater or smaller), the resonant analysis can be shifted to any frequency.

3. TCSs for two RCAs and their mutual couplings

Before investigating the TCSs of the two RCAs, it is necessary to define the RCA configurations. The case wherein two dipole antennas are arranged in the longitudinal direction, as depicted in Figure 4(a), is called the collinear case. On the other hand, that in which two dipole antennas are arranged laterally, as shown in Figure 4(b), is called the side-by-side case. Next, we considered the RCA arrangements. When electromagnetic waves are excited on the RCA, the incident electric field is concentrated between the upper and lower ridges and is formed along the width direction (along the x-direction) of the ridges, as shown in Figure 4(c). From this development, the equivalent magnetic current $$ \overrightarrow{M}$$ is described in red, and it can be seen that the two current elements are arranged collinearly. Finally, when the RCAs are arranged in the y-axis direction, as shown in Figure 4 (d), the equivalent magnetic currents $$ \overrightarrow{M}$$ are formed, as shown in red, which indicates that the two current elements are arranged side-by-side.

Figure 4:

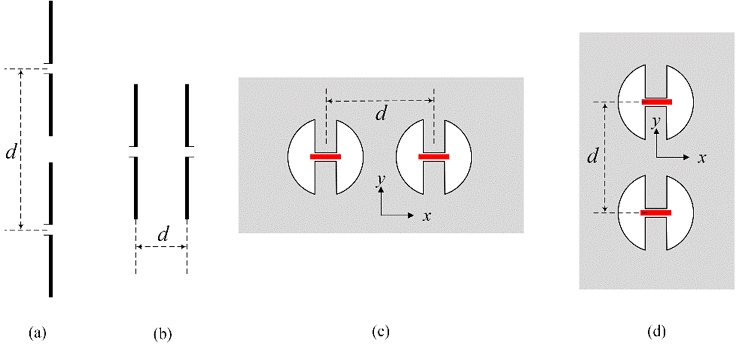
Array definitions according to arrangements of two dipole antennas and two RCAs. (a) Collinear and (b) side-by-side arrangements of the two dipoles. (c) Collinear and (d) side-by-side arrangements of the RCAs. The center-to-center distances of d are described for each case.

We considered TCS variations when two RCAs were arranged. Because Case B2 was considered the basic type of aperture, we obtained TCSs when two Case B2s were applied. As the electric field is intensively induced between the two ridges of a single RCA, it can only be concentrated along the x-axis, as shown in Figure 1. We assume that this could be a short slot corresponding to the duality of a half-wavelength dipole antenna, and then the arrangement types can be classified according to the direction of the concentrated electric field.

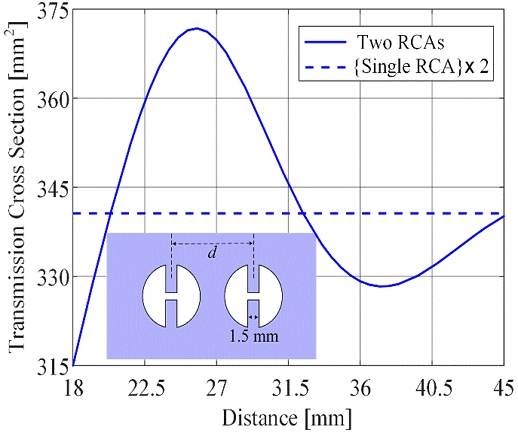
First, the RCAs corresponding to Case B2 in Figure 2 are assumed to be arranged in the collinear direction [12], as shown in the inset of Figure 5(a). The variation in the TCSs according to the center-to-center distance d can be calculated using the FDTD formulation, as depicted by the solid line in Figure 5(a). The total TCS, determined simply by multiplying the TCS for a single RCA of Case B2 by two, can be expressed as a dashed line and compared with the solid line. Thus, when the two RCAs are very close, strong mutual coupling does not occur, and the TCS is too low. However, when the distance between the two RCAs increases and is set optimally, the corresponding TCS is maximized. In this case, the distance was 26.7 mm, and the maximum TCS was 395.08 mm². By converting this value to the wavelength, it becomes approximately 0.981λ. Similarly, when two half-wavelength dipole antennas are arranged collinearly, the maximum gain ratio of the antenna is obtained when the center-to-center distance d is approximately 1.0λ [12]. (The gain ratio is to the half-wavelength dipole antenna what the TCS is to the RCA.) Therefore, it can be seen that the duality is satisfied by two different resonant structures. As the distance d increases, the center-to-center distance at which the minimum TCS is obtained is approximately 38.55 mm (1.42λ), and the corresponding TCS is 348.32 mm². Similarly, when two half-wavelength dipole antennas are collinearly aligned, a center-to-center distance of approximately 1.46λ for the minimum gain ratio is achieved. As the center-to-center distance d continuously increases, the two TCSs for each RCA seem to be independently considered. Therefore, it can be understood that the fluctuation in the solid line progresses toward and converges on the dashed line, which is the same phenomenon for collinearly arranged half-wavelength dipole antennas. Then, duality is also satisfied.

Figure 5:

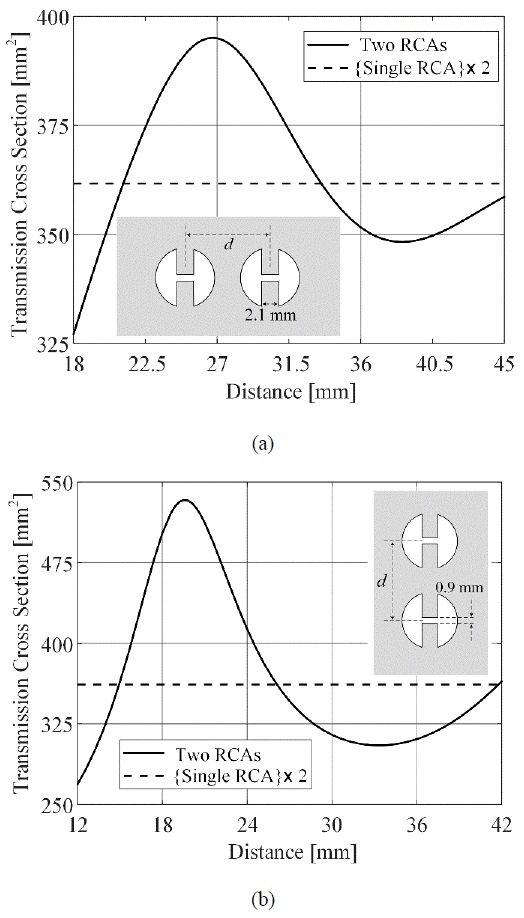
TCSs versus center-to-center distances for (a) collinear and (b) side-by-side arrangements in Case B2.

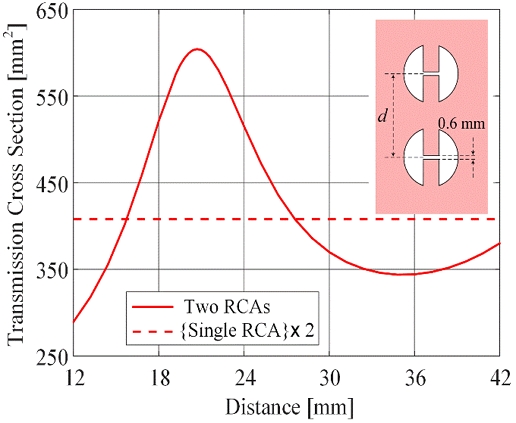
Second, the geometry where the two RCAs in Case B2 (see the inset of Figure 5(b)) are arranged side-by-side can now be considered. Similar to the collinear case, the induced electric field is concentrated on the x-axis in the gap between the two ridges. The case wherein the x-directional electric fields of two RCAs are parallel is defined as the side-by-side case, which can correspond to the side-by-side case of the half-wavelength dipole antenna [12]. The solid line in Figure 5(b) represents the TCS of the two RCAs in a side-by-side arrangement as the center-to-center distance d varies. Like the dashed line in Figure 5(a), the total TCS, found merely by multiplying the TCS for a single RCA in Case B2 by two, can be plotted as the dashed line in Figure 5(b). When the two RCAs are very close (see the solid line in Figure 5(b)), the mutual coupling phenomenon becomes weak, and the corresponding TCS is too low, whereas the TCS increases when the distance reaches the optimum level. This phenomenon is similar to that in the collinear case, but the fluctuation range in Figure 5(b) is much greater than that in Figure 5(a). It was found that these different mutual couplings between the two RCA arrangements were very similar to the arrangements of the two half-wavelength dipole antennas. When the center-to-center distance d for the side-by-side arrangement reaches 19.5 mm, a maximum TCS of 533.35 mm² is obtained. If the metric distance is transformed into wavelength, 19.5 mm becomes approximately 0.716λ. Let us consider two half-wavelength dipole antennas arranged side by side. The maximum gain ratio is obtained when the center-to-center distance of the arrangement reaches approximately 0.7λ [12]. Therefore, it can be said that two different arrangements also constitute duality. For the minimum TCS, the distance d is obtained at approximately 33.6 mm (1.234λ), and the corresponding TCS is 305.15 mm², as represented in Figure 5(b). Similarly, when two half-wavelength dipole antennas are arranged side by side, the center-to-center distance d for the lowest gain ratio is approximately 1.24λ, unless they are arranged very closely (i.e., less than 0.7λ). When the center-to-center distance d increases infinitely, it is as if double TCSs from two independent single RCAs are considered. Therefore, the fluctuation in the solid line continues as d increases and converges on the dashed line. Thus, duality with a half-wavelength dipole antenna arrangement is satisfied.

Finally, we determined whether the TCS trends in Figure 5 could be similarly applied even when the shape of the ridge was changed. Among the cases shown in Figure 2, the TCSs for Cases A2 and B3 as a function of distance were examined for the collinear and side-by-side arrangements, respectively. The resonant frequencies and TCSs in Cases A2 and B3 are listed in Tables 2 and 1, respectively.

As shown in the inset of Figure 6, when the width of the ridge is reduced to 1.5 mm, the TCS characteristics as a function of distance d are calculated, and the double TCSs (= 340.64 mm²) at a resonance frequency of 11.42 GHz are represented by the dashed line in Figure 6. A similar collinear TCS trend can be observed in Figure 5(a), but a TCS difference in scale occurs. For the wavelength at the resonant frequency in Case A2, the distance d where the maximum TCS of 371.760 mm² occurs is approximately 0.982λ (25.8 mm), and the distance d where the minimum TCS of 328.320 mm² occurs is approximately 1.4λ (36.6 mm). These wavelengths are very similar to the distances represented by the wavelengths at which the maximum and minimum TCSs occur, as shown in Figure 5(a). Similarly, as shown in the inset of Figure 7, when the gap between the ridges is reduced to 0.6 mm, TCS characteristics as a function of distance d are obtained, and the double TCSs (408 mm²) at the resonant frequency of 10.36 GHz are depicted as a dashed line in Figure 7. A similar side-by-side TCS trend can be observed in Figure 5(b); however, a TCS difference in scale appears. For the wavelength at the resonant frequency in Case B3, the distance d where the maximum TCS of 604.253 mm² occurs is approximately 0.715λ (20.7 mm), and the distance d where the minimum TCS of 343.943 mm² occurs is approximately 1.2λ (34.8 mm). These wavelengths are very similar to the distances indicated by the wavelengths at which the maximum and minimum TCSs occur, as shown in Figure 5(b). From Figures 6 and 7, it can be understood that even if the geometry of the RCA is changed, the TCS trend with respect to the distance remains similar for both the collinear and side-by-side RCA arrangements. Because these TCS variations are very similar to the changes in the gain ratios of the arrangement of half-wavelength dipole antennas, it can be confirmed that the duality between the RCA and half-wavelength dipole antenna is satisfied.

Figure 6:

TCS versus the center-to-center distance for the collinear arrangement in Case A2.

Figure 7:

TCS versus the center-to-center distance for the collinear arrangement in Case B3.

5. Conclusion

In this study, the resonant transmission phenomenon for a single RCA was investigated, and the TCSs were calculated according to changes in the ridge shape and the corresponding resonance frequency shifts. Moreover, the transmission characteristics as a function of the distance between the two RCAs were examined when the two RCAs were arranged collinearly and side by side. It was confirmed that even if the ridge shape is changed delicately, the overall TCS trends are not significantly different. Furthermore, it was found that these phenomena are similar to the maximum and minimum gain ratios when the dipole antennas are collinear or side by side; thus, duality was satisfied for both geometries. These results can be applied to frequency-selective surface design.

Acknowledgments

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No. 2020R1G1A1102288).

References

• H. A. Bethe, “Theory of diffraction by small holes,” Physical Review Journals Archive, vol. 66, no. 7-8, pp. 163-182, 1944. [https://doi.org/10.1103/PhysRev.66.163]
• R. F. Harrington, “Resonant behavior of a small aperture backed by a conducting body,” IEEE Transactions on Antennas & Propagation, vol. 30, no. 2, pp. 205-212, 1982. [https://doi.org/10.1109/TAP.1982.1142761]
• X. Shi, and et al., “Ultrahigh light transmission through a C-shaped nanoaperture,” Optics. Letters, vol. 28, no. 15, pp. 1320-1322, 2003. [https://doi.org/10.1364/OL.28.001320]
• F. M. Kong, and et al., “Propagation properties of the SPP modes in nanoscale narrow metallic gap, channel, and hole geometries,” Progress in Electromagnetics Research, vol. 76, pp. 449-466, 2007. [https://doi.org/10.2528/PIER07070203]
• F. M. Kong, and et al., “Analysis of the surface magnetoplasmon modes in the semiconductor slit waveguide at terahertz frequencies,” Progress in Electromagnetics Research, vol. 82, pp. 257-270, 2008. [https://doi.org/10.2528/PIER08031224]
• J. -E. Park, and et al., “Analysis of deep-subwavelength Au and Ag slit transmittances a terahertz frequencies,” Journal of the Optical Society America B, vol. 33, no. 7, pp. 1355-1364, 2016. [https://doi.org/10.1364/JOSAB.33.001355]
• J. -E. Park, and et al., “Resonant transmission of an electrically small aperture with a ridge,” Journal of Electromagnetic Waves and Application, vol. 23, no. 14-15, pp. 1981-1990, 2009. [https://doi.org/10.1163/156939309789932502]
• J. -E. Park, and et al., “Resonant power transmission through coupled subwavelength ridged circular apertures,” Journal of Electromagnetic Waves Applications, vol. 26, no. 4, pp. 423-435, 2012. [https://doi.org/10.1163/156939312800030686]
• J.-E. Park, and et al., “Comparison of mutual coupling phenomena in subwavelength ridged circular apertures and half-wavelength dipole antenna arrays,” International Journal of Antennas and Propagation, vol. 2012, 129469, 2012. [https://doi.org/10.1155/2012/129469]
• A. Taflove and S. C. Hagness, Computational Electrodynamics: The Finite-Difference Time-Domain Method, Norwood, USA, Artech House, 2005. [https://doi.org/10.1002/0471654507.eme123]
• L. Verslegers, and et al., “Temporal coupled-mode theory for resonant apertures,” Journal of the Optical Society of America B, vol. 27, no. 10, pp. 1947-1956, 2010. [https://doi.org/10.1364/JOSAB.27.001947]
• P. S. Carter, “Circuit relations in radiating systems and applications to antenna problems,” Proceedings of the Institute of Radio Engineers, vol. 20, no. 6, pp. 1004-1041, 1932. [https://doi.org/10.1109/JRPROC.1932.227723]