A study on the optimal tracking problems with predefined data by using iterative learning control
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In this paper, we present an iterative learning control (ILC) framework for tracking problems with predefined data points that are desired points at certain time instants. To design ILC systems for such problems, a new ILC scheme is proposed to produce output curves that pass close to the desired points. Unlike traditional ILC approaches, an algorithm will be developed in which the control signals are generated by solving an optimal ILC problem with respect to the desired sampling points. In another word, it is a direct approach for the multiple points tracking ILC control problem where we do not need to divide the tracking problem into two steps separately as trajectory planning and ILC controller.The strength of the proposed formulation is the methodology to obtain a control signal through learning law only considering the given data points and dynamic system, instead of following the direction of tracking a prior identified trajectory. The key advantage of the proposed approach is to significantly reduce the computational cost. Finally, simulation results will be introduced to confirm the effectiveness of proposed scheme.
Keywords:
Iterative learning control, Optimal tracking, predefined data points, Without a reference trajectory, Direct tracking1. Introduction
Control schemes for tracking problems can be divided into two steps: trajectory planning and tracking control. In these schemes, the trajectory planner attempts to generate an optimal reference trajectory from a given set of points in the motion profile (i.e., specified data points that are desired points at some specified time instants). Then the controller, which is designed to track the reference trajectory, focuses on the system dynamics to generate a sequence of inputs. To improve the performance of trajectory tracking, various control schemes such as feedback control, robust control, and iterative learning control have been developed.
Iterative learning control (ILC) is a control methodology for tracking a reference trajectory in repetitive systems, found in applications such as robotics, semiconductors, and chemical processes. The prime strategy of ILC algorithms is to refine the input sequence from one trial in order to improve the performance of the system on the next trial. Anumber of surveys[1]-[3] have effectively covered the novel ideas and development of ILC methodology and can be referred for more information on the basic ideas of ILC.
As discussed in related works [2][4][5] dividing the tracking problem into trajectory planning and ILC trajectory tracking shows drawbacks under certain circumstances. For that reason, this paper proposes and analyzes a direct approach for the multiple points tracking ILC control problem where it does not need to divide the tracking problem into two steps separately.
The strength of the proposed formulation is the methodology to obtainlearning laws only considering the given data points anda control signal throughdynamic system, instead of following the direction of tracking a prior identified trajectory. In effect, it may not be necessary to plan a reference trajectory as conventional approaches and to reduce the computational cost.
As mentioned, most ILC algorithms focus on tracking a fixedreference trajectory. There have been fewer studies on the connection between the trajectory planning and ILC control algorithms, although there is increasing interest in this topic. In terminal ILC, which considers only one end point as a desired output point, Xu et al [6] and Gauthier et al. [5] have addressed the relationship between a point in the motion profile and the control update. Recently, there has been a series of works that consider the tracking problem with multiple specified data points [4][7]-[9] with a particular application to stroke rehabilitation to assist point-to-point movements of patients [10]. These works have shown that, the performance of multiple points tracking problems could be improved based on ILC techniques. Specifically, in [4], the authors developed an ILC framework in which the reference trajectory is updated. Similar to Freeman et al. [4] tracking problems with multiple pass points at specified time are also consideredbut in this paper, a novel approach for tracking problems with multiple pass points at specified data points is proposed. That is a direct tracking control without a reference trajectory.
The remainder of this paper is organized as follows. The formulation of tracking problem and the conventional approach to solving the problem is provided in Section 2. Section 3 proposesan ILC algorithm where the control signals aregenerated by solving an optimal ILC problem with respect to the desired sampling points. Simulation results are given in Section 4, and Section 5 concludes this work.
2. Tracking Problemwith Specified Data Points
Similar to work in Le et al. [11], consider a linear, continuous-time system that operates on an interval t∈ [0, Τ] as
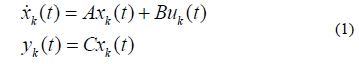
where, k is the iteration index. The system is a MIMO system that has state
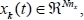control signal
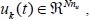and output
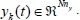The matrices A, B and C have appropriate dimensions. In the tracking problem, the system trajectory must pass through, or close to, a limited number of specified points, at prescribed times. The specified time instants in the system operation are defined from the set
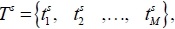where
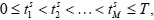and the desired outputs at these points are given by
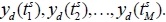As a result, the control task is to construct a control law that drives the system output to go through the desired values as closely as possible:.
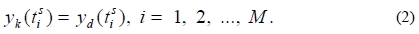
In typical tracking schemes, a trajectory planner generates a reference trajectory r(t) such that it passes the desired points at
In the trajectory planning stage, one of the common techniques to find a reference trajectory from the given points is ‘‘interpolating splines’’, which is a tool in numerical analysis. The generated function is a spline if it exactly interpolates the given points[12]. However, the reference trajectory may not be feasible for the system since it may vary too fast to allow the dynamics to follow the trajectory or it may vary too slowly, which gives a conservative control performance. Thus, the control theoretic interpolating splines were introduced in [13]. The suggested approach addresses these problems by considering auxiliary system dynamics, rather than the spline functions.
In a typical problem, after a trajectory has been generated, a tracking control is applied. To illustrate, consider the case where a linear discrete-time system operates repetitively, from the same initial condition at the start of each trial and we suppose an ILC controller is applied to drive the system output to go as close as possible to the reference trajectory. In ILC, the learning algorithm utilizes output errors and control inputs from the previous iterations to compute an updated control signal in [3][14]. To describe this, let the discrete-time system be described in the lifted system framework as
where the input signal, output signal, and reference trajectory are written in the super-vector forms as
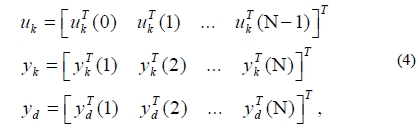
and the system matrix P = [pij] is a Markov matrix which is a lower triangular Toeplitz matrix. For this system we then adopt the following ILC algorithm:
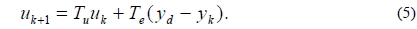
It is well known that, this ILC algorithm is convergent if ρ(Τu - ΤeP) < 1. where ρ(A) < 1 is the spectral radius of the matrix A. The algorithm guarantees a monotonic convergence if ρ(Τu - ΤeP) < 1 the condition where ρ(A) < 1 is the largest singular value of the matrix A, is satisfied. The tracking problem we are interested in, then, is to force the continuous-time system (1) or the discrete-time system (3) to pass through (or close) to the desired points (2) using an algorithm such as Equation (5). In the next section an approach is proposed to solve this problem.
3. Direct Tracking Control without a Reference Trajectory
3.1 Optimal ILC
Let us consider the equivalent linear discrete-time invariant system (3), where t = 0, 1, 2, . . .,N-1.
Define
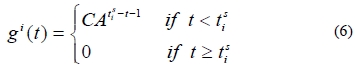
the output at the i-th specified time instant is expressed by
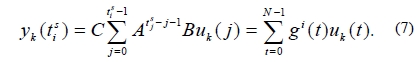
where,
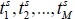is pre-specified time of M desired points.
The cost function for the problem of tracking multiple desired points in the discrete time model is given as
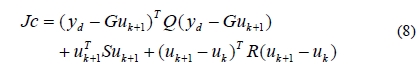
where, R, S = (rI, sI), Qare positive definite matrices,
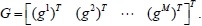The controller in the(k+1)-th trial is achieved from the condition
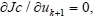or
where, Wd = GGT is a symmetric positive definite matrix.
Matrix ((r+s)I +QWd) is non-singular, by defining
the ILC control algorithm for given system is derived as follow
In definition, the L2-norm of the control signal is
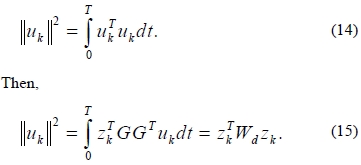
Since Wd is a positive definite matrix, Wd=VTV, in which V has independent columns, leads to
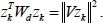
Therefore,
Consequently, the convergence of the control signal is guaranteed from the convergence of the kzlearning algorithm because of Equation (13). Then, the control input generated by Equation (13) will drive the system output through or close to the desired motion profile.
Moreover, from (11):
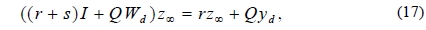
or,
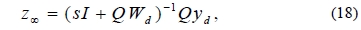
Then the control input converges to a fixed point u∞ as:
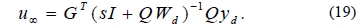
As a result, the error converges to a fixed point e∞ as:
Furthermore, if Q = qI, where q is real positive, the algorithm achieves monotonic convergence. The reason is that now the matrix ((r + s) I + QWd)-1r is a symmetric positive definite matrix which has the largest singular value equals its spectral radius, and ρ ((((r + s) I + QWd)-1r) [15].
3.2 Theory Analysis
Here, it is clear to see a significant decrease of the computational analyses. In proposed learning algorithm, vector Zk ∈ RM and Lz, Le are mMxmM matrices where M is the number of terminal points. In comparison, the typical ILC algorithm updates the input with the system matrix mN×mN. As the length of iteration increases (N>1000), which is common in many applications such as robotics with a high sampling rate, the requirement of memory and time dramatically increases.
3.3 Input Constraints
Many control applications require constraints on the control signal ziuk+1 and its change with time δuk+1 due to physical limitations or performance requirements. Furthermore, the constraint on the change of input in the iteration domain ∆uk+1 should be incorporated.
Consider the constraints as
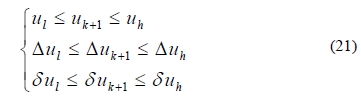
where,
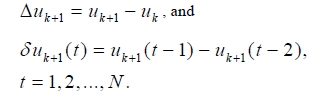
Note that the constraints are chosen to be feasible. Here, δuk+1 can be rewritten as
where, E is a N×N matrix and,
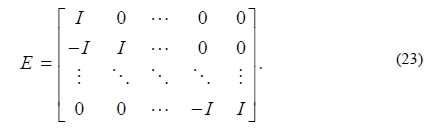
Thus, the given constraints can be combined into the following constraints equation:
where,
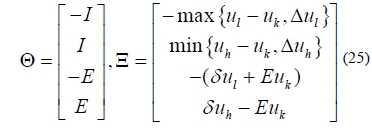
or equivalently,
Sincek+1 = ek - Wd∆zk+1, uk+1 = GT (∆zk+1 + zk), the problem of minimizing the cost function Jc in Equation (8) is derived as
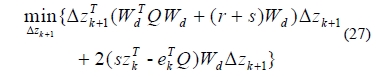
As a result, the given minimization together with the constraints Equation (26)represents a standard quadratic programming problem. In addition, the solutions were proposed in[7][15].
4.Simulation Results
Performances of the proposed techniques are presented through an example of the tracking problem with a linear discrete-time system model to show advantages of the proposed method without reference trajectory. The proposed approach will be compared with the conventional approach.
The chosen system isthe same in [11]which is shown inEquation (28)which operates on interval t ∈ [0, 79]. 5 points are selected as desired points in the motion profile, such as: (16, 10), (32, 28), (48, 8), (64, 12), (80, 16). Simulation is shown in Figures 1-5 as following.
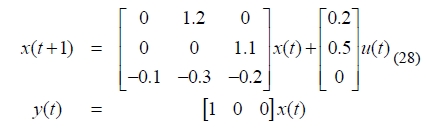
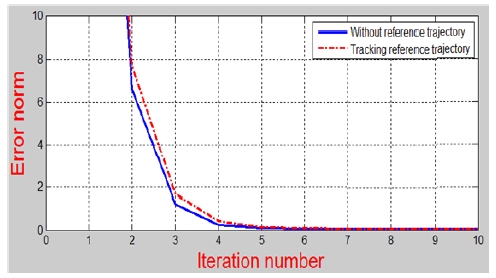
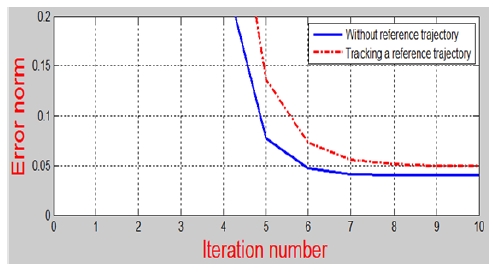
Figure 1 shows the norm of errors in linear scale versus iteration number of proposed approach. Figure 2 depicts a detail view for norm of error. As shown in Figure 1 and Figure2, the tracking error converges close to a constant error and the convergent rate of error under proposed ILC algorithm without any reference trajectory is slightly better than the method of work in [11].
Performance of the ILC controller without reference trajectory with q = 20, r = 2, and s = 0.01.
Detail norm of error of system under proposed ILC controller with q = 20, r = 2 and s = 0.01.
Output of system under proposed ILC controllerwith q = 20, r = 2 and s = 0.01.
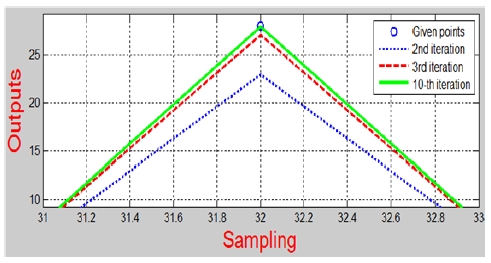
Figure 3 and Figure 4 illustrate achieved actual outputs of given system under proposed ILC controller. Accordingly, based on suitable chosen weighting matrices, the controller produces superior performance; specifically, output signals go through, or very close to, desired given data points after some iteration.
Detail output of system under proposed ILCcontroller with q = 20, r = 2 and s = 0.01.
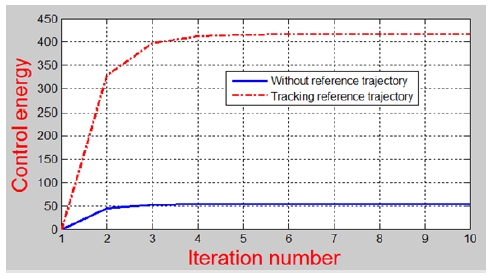
By comparison, the conventional norm optimal solution of tracking the given reference trajectory is also simulated in Figure 5. It can be seen that the proposed ILC law achieves significantly decrease of control energy, while increasing rate of convergence.
Comparison of control energy between the proposed controller and the conventional ILC (q = 20, r = 2, and s = 0.01).
5. Conclusion
This paper has presented optimal tracking strategies for problems where the system must pass through or close to desired data points at given specified time instants, for the case of systems that repeat their operation from the same initial conditions at each trial. Taking an iterative learning control approach, we have proposed an idea of using only the essential information of the specified data points without building the desired trajectory along the iteration. We showed that, this approach is better in both performance and control efforts, relative to the conventional ILC approaches. Here we have considered only linear systems from an optimization point of view. Future work will consider nonlinear systems as well as linear systems with model uncertainties.
Acknowledgments
The research was supported by the Green Marine Equipment RIS Center Program through the Ministry of Trade, Industry & Energy (MOTIE).
This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2014), held at Paradise Hotel, Busan, Korea on September 17-19, 2014.
References
- D. A. Bristow, M. Tharayil, and A. G. Alleyne, “A survey of iterative learning control: A learning-based method for high-performance tracking control”, IEEE Control Systems Magazine, 26(3), p96-114, (2006).
-
H. S. Ahn, Y. Q. Chen, and K. L. Moore, “Iterative learning control: Brief survey and categorization”, IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews, 37(6), p1099-1121, (2007).
[https://doi.org/10.1109/TSMCC.2007.905759]
-
K. L. Moore, “Iterative learning control: An expository overview”, Journal of Applied and Computational Control, Signals, and Circuits, 1(1), p151-214, (1999).
[https://doi.org/10.1007/978-1-4612-0571-5_4]
-
C. T. Freeman, Z. Cai, E. Rogers,, and P. L. Lewin, “Iterative learning control for multiple point-to-point tracking application”, IEEE Transactions on Control Systems Technology, 19(3), p590-600, (2011).
[https://doi.org/10.1109/TCST.2010.2051670]
-
G. Gauthier, and B. Boulet, “Terminal iterative learning control design with singular value decomposition decoupling for thermoforming ovens”, Proceedings of the American Control Conference, p1640-1645, (2009).
[https://doi.org/10.1109/ACC.2009.5160445]
-
J. X. Xu, and D. Huang, “Initial state iterative learning for final state control in motion systems”, Journal of Automatica, 44(12), p3162-3169, (2008).
[https://doi.org/10.1016/j.automatica.2008.05.017]
-
C. T. Freeman, Y Tan, “Point-to-point iterative learning control with mixed constraints”, Proceedings of American Control Conference, p3657-3662, (2011).
[https://doi.org/10.1109/ACC.2011.5991198]
-
C. T. Freeman, C. Zhonglun, P. L. Lewin, and E. Rogers, “Iterative learning control for multiple point-to-point tracking”, Proceedings of the 48th IEEE Conference on Decision and Control, p3288-3293, (2009a).
[https://doi.org/10.1109/CDC.2009.5399918]
-
C. T. Freeman, C. Zhonglun, P. L. Lewin, and E. Rogers, “Objective-driven ILC for point-to-point movement tasks”, Proceedings of American Control Conference, p252-257, (2009b).
[https://doi.org/10.1109/ACC.2009.5159965]
- C. T. Freeman, E Rogers, A. M. Hughes, J. H. Burridge, and K. L. Meadmore, “Iterative learning control in healthcare electrical stimulation and robotic-assisted upper limb stroke rehabilitation”, IEEE Control Systems Magazine, 32(1), p18-43, (2012).
- D. K. Le, and T. K. Nam, Nam,“Performance improvement of trajectory tracking control by using ILC”, Proceedings of the 38th KOSME Spring Conference, p194, (2014).
- A. D. Luca, L. Lanari, and G. A. Oriolo, “Sensitivity approach to optimal spline robot trajectories”, Journal of Automatica, 27(3), p535-539, (1991).
-
S. Sun, M. Egerstedt, and C. F. Martin, “Control theoretic smoothing spline”, IEEE Transactions on Automatic Control, 45(12), p2271-2279, (2000).
[https://doi.org/10.1109/9.895563]
- N. Amann, D. H. Owens, and E. Rogers, “Iterative learning control using optimal feedback and feed forward actions”, International Journal of Control, 65(2), p277-293, (1996).
- D. K. Le, and T. K. Nam, “Optimaliterative learning control with model uncertainty”, Journal of the Korean Society of Marine Engineering, 37(7), p743-751, (2013).
- J. X. Xu, and J. Xu, “Iterative learning control for nonuniform trajectory tracking problems”, Proceedings of the 15th IFAC World Congress, p1048-1048, (2002).