PSO based tuning of PID controller for coupled tank system
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This paper presents modern optimization methods for determining the optimal parameters of proportional-integral-derivative (PID) controller for coupled tank systems. The main objective is to obtain a fast and stable control system for coupled tank systems by tuning of the PID controller using the Particle Swarm Optimization algorithm. The result is compared in terms of system transient characteristics in time domain. The obtained results using the Particle Swarm Optimization algorithm are also compared to conventional PID tuning method like the Ziegler-Nichols tuning method, the Cohen–Coon method and IMC (Internal Model Control). The simulation results have been simulated by MATLAB and show that tuning the PID controller using the Particle Swarm Optimization (PSO) algorithm provides a fast and stable control system with low overshoot, fast rise time and settling time.
Keywords:
Coupled tank systems, Proportional-integral-derivative controller, Particle swarm optimization, Ziegler-nichols tuning rule, Cohen–coon method, Internal model control1. Introduction
PID control is a generic feedback control technology and it makes up 90% of automatic controllers in industrial control systems. The popularity of PID controllers is due to their functional simplicity and reliability. They provide robust and reliable performance for most systems and the PID parameters are tuned to ensure a satisfactory closed loop performance. Setting of the proportional, integral and derivative values of PID controller to get the best possible control for a process using a tuning algorithm is called tuning of PID controller [1].
The control system performs poor in characteristics and it even becomes unstable, if improper values of the controller tuning constants are used [2]. Setting of the proportional, integral and derivative parameters of a PID controller to get the best control result for a process using a tuning algorithm is called tuning of a PID controller. So it becomes necessary to tune the PID controller to achieve good control performance with the proper choice of PID parameters. The basic function of PID controller is to use a proper tuning algorithm and to maintain the output in the desired or required output. Among the well-known formulas is the Ziegler–Nichols tuning method [3], the Cohen–Coon method [4], and internal model control (IMC) [5].
In spite of the enormous amount of research works reported in literature, many PID controllers are poorly tuned in practice. One of the reasons is that most of the tuning methods are derived for particular processes, experiments and situations, and therefore apply well only to their own area [6].
This paper attempts to develop a PID tuning method using PSO algorithm. The result is expected to show the effectiveness of the modern optimization such as PSO (Particle Swarm Optimization) in control engineering applications especially.
PSO algorithm is a stochastic algorithm based on principles of natural selection and search algorithm. There is much evidence of intelligence for the posed domains in animals, plants, and living systems in general. For example, ants foraging, birds flocking, and fish schooling are some well-known examples.
In this paper, a PSO based tuning approach is used to design a PID controller for a coupled tank system. Obtained results are compared with other existing techniques in terms of system transient characteristics and performance index.
2. Dynamic Model of Coupled Tank System
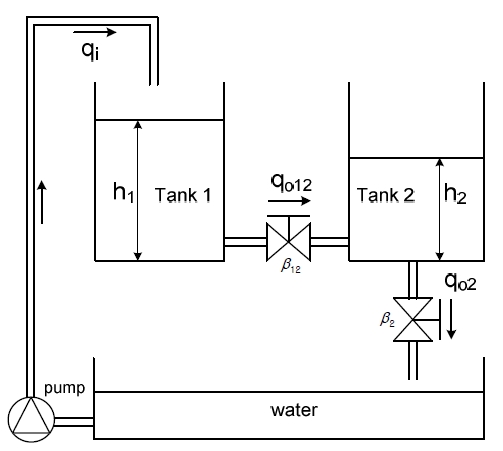
The schematic diagram of coupled tank as SISO process as shown in Figure 1. Two tanks are connected in an interactive valve. The inflow of tank 1 is qi and outflow of tank 2 is qo2. The control variable is level in tank 2.
The coupled tank system.
According to Figure 1 the input u is the input voltage which is taken to the pump, and the output h2 is the water level in tank 2.
The nonlinear equation can be obtained by mass equivalent equation and Bernury’s law is given by.
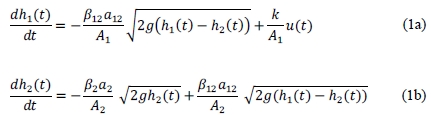
where A1 and A2 are the cross section area (cm2) of tank 1 and tank 2, a2 is the cross section area (cm2) of outlet of tank 2, a12 is the cross section area (cm2) of jointed pipe between tank 1 and tank 2, β2 is the value ratio at the outlet of tank 2, β12 is the value ratio between tank 1 and tank 2, g is the gravity (cm/s2) and k is the gain of pump (cm3/V × s).
According to Equation (1), linearized model is given by Equation (2).
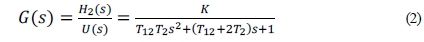
where T12 is the time constant between tank 1 and tank 2, and T2 is the time constant of tank 2. T12, T2 and K can be obtained the Equation (3) as following.
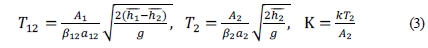
where h1 and h1 is the water level at operating point of coupled tank system.
3. Particle Swarm Optimization
3.1 Feature of PSO algorithm
Kennedy and Eberhart [7] proposed a swarm intelligence-based parallel optimization algorithm, Particle Swarm Optimization (PSO) in 1995.
PSO is a computational algorithm technique based on swarm intelligence. This method is motivated by the observation of social interaction and animal behaviors such as fish schooling and bird flocking.
The PSO method is a population based search algorithm where each individual is referred to as particle and represents a candidate solution. Each particle flies through the search space with an adaptable velocity that is dynamically modified according to its own flying experience and also the flying experience of the other particles [8]-[10].
In PSO, each particle strives to improve itself by imitating traits from their successful peers. Further, each particle has memory and therefore is capable of remembering the best position in the search space ever visited.
The best previous position (giving the minimum fitness value) of any particle is recorded and represented as PI =(pi1, pi2,⋯, pD), this is called pbest (pid, refer to Equation (6)). The index of the best particle among all particles in the population is called as gbest (pgd, refer to Equation (6)).
It was developed through simulation of a simplified social system, and has been found to be robust in solving continuous nonlinear optimization problems [11]-[13]. The PSO algorithm can generate a high-quality solution within shorter calculation time and stable convergence characteristic than other stochastic methods [13][14]. Much research is still in progress for proving the potential of the PSO in solving complex system problems.
In PSO algorithm [11][14], each particle in swarm represents a solution to the problem and is defined with its position and velocity. The mathematical description of the basic particle swarm optimization is as follows.
Supposing the scale of swam is N, the position of particle i can be expressed as:
The velocity of the particle is defined as the distance of the particle movement in the each iteration, described as Equation (5).
And the velocity of the particle I (i=1, 2,⋯,N) in the d (d=1, 2, ⋯,D)–dimensional space which is adjusted according to Equation (5) is:
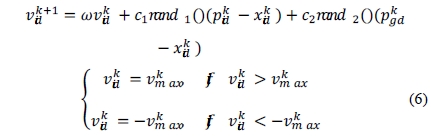
Equation (6) is used to calculate the particle’s new velocity according to its previous velocity and the distances of its current position from its own best experience (position) and the group’s best experience. Finally, the particle flies toward a new position according to Equation (7).
where N is the number of particles in the group, d is the imension, vid is the velocity of particle i, c1 and c2 is the acceleration constant, rand() is the random number between 0 and 1, k is an iteration number, xid is the current position of particle i, Pid is the best previous position of the ith particle, pgd is the best particle among all the particles in the population.
Inertia weight (ω) is brought into the equation to balance between the global search and local search capability [10]. It can be a positive constant or even a positive linear or nonlinear function of time.
3.2 PSO based PID controller
In this paper, a PID controller using the PSO algorithm was developed to improve the step transient response of the coupled tank system. The PSO algorithm was mainly utilized to determine three optimal controller parameters: Kp, Ki and Kd, and, such that the controlled system could obtain a good step response output.
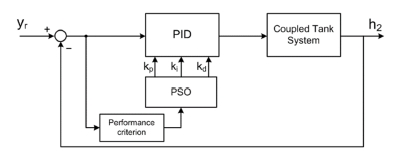
The structure diagram of PSO based PID control system is shown in Figure 2.
Structure of PSO based PID control system
This controller is designed mainly for the following two components: the PID controller for the coupled tank system and the module of the PSO algorithm.
According to the operating state of the system, the module of PSO can optimize the parameters of the PID controller to meet the performance requirements, and the output of this module will provide the optimized parameter of PID controller.
And now, the performance criterion in PID controller is described as follow:
where tf is the expected settling time and IAE means the integral of absolute error.
3.3 Implementation of PSO-PID Controller
The implementation steps of parameter optimization of PID controller based on PSO can be divided as follow:
Step 1) Initialize the number of the particle (Population size):
Population size affects the performance of the PSO algorithm. It is easy to get local optimal solution, if the population size is small. If the population size is too large, it is difficult and time-consuming to realize, which will exponentially increase the complexity of the algorithm. In this paper, the population size is set to 100.
Step 2) Initialize the particle dimension:
The number of the particle dimension is determined by the optimized object. The outputs of the PSO module are the three parameters of PID controller, such as Kp, Ki and Kd, so the particle dimension is set to 3.
PSO firstly produces initial swarm of particles in search space represented by matrix. Each particle represents a candidate solution for PID parameters. For this 3-dimentional problem like this paper, position and velocity are represented by matrices with dimension of 3×Swarm size. The Swarm size means population size, and in step 1) we already set to 100.
Step 3) Determine the fitness value:
Calculate the fitness value of each particle through the integral of absolute error,
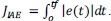
Step4) Analysis of fitness value and update:
To analysis the fitness value of each particle, and update the global optimum position value.
Step 5) Update the velocity and position of the particle.
Step 6) Stop condition
If the maximum iteration number comes to the end or the performance criteria is satisfactory, the PSO gets the optimal parameters of PID controller. Otherwise, it returns to step 3).
Finally, in this work, the initial value of the particles is randomly generated within a certain space. The other parameters are chosen as follows: ω (Inertia weight factor)=0.5, c1=1.2, c2=0.12, iteration =100.
4. Simulation Results
For the coupled tank as SISO process the parameters are obtained by experimental results or data sheet and the parameters including the operating point of the process as shown in Table 1.
Parameters of coupled tank system
Using the Table 1 and Equation (2), the transfer function in operating points is as below.
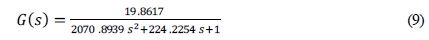
4.1 Verification of the FOPTD estimation model
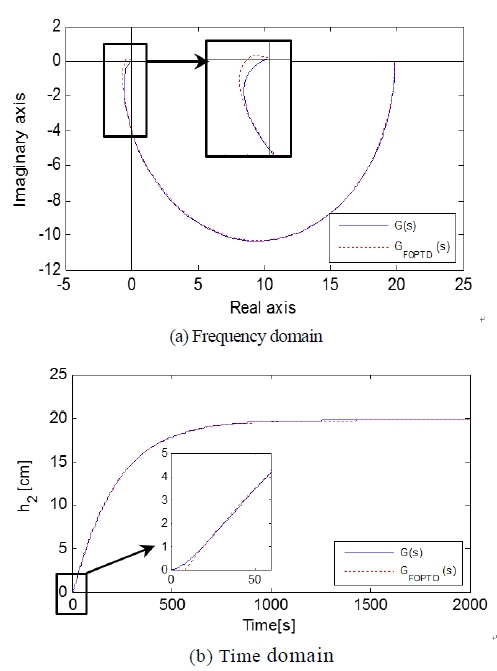
In this paper the PSO tuning technique is compared with other tuning methods. Therefore Equation (9) needs to approximate as FOPTD (First Order Plus Time Delay) model. In this paper, G(s) is approximated as FOPTD models using least square method (LSM), and the estimated model is as follow:
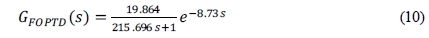
As shown in Figure 3, the estimated FOPTD model is consistent with the G (s) in the time domain and the frequency domain. A slight mismatching is observed near the origin in the frequency domain due to the time delay term of FOPTD model.
Verification of FOPTD model estimation model
4.2 Performance related to steady state condition
The PSO module passes the initial value of the particles to coupled tank system module. Then, the system module calculates the fitness value that based on the performance criteria (IAE) and outputs it to the PSO module. So the cycle to repeat, until the maximum iteration number comes to the end.
The design takes the step signal as input signal to achieve the step response of the control system, which is shown in Figure 2.
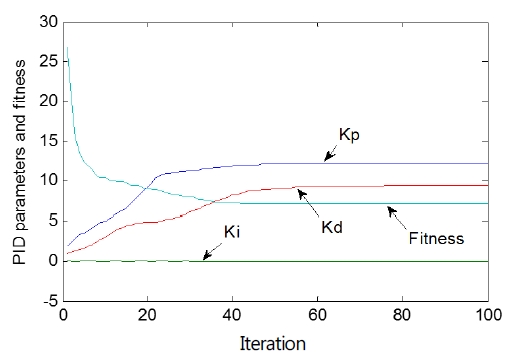
The curves of the global optimal fitness value and PID parameters are shown in Figure 4. Based on PSO for the application of the PID tuning we get the PID tuning parameters as Kp=12.144, Ki=0.030, and Kd=9.349. Using the PSO approach, global and local solutions could be simultaneously found for better tuning of the controller parameters.
Fitness and PID parameters based on PSO
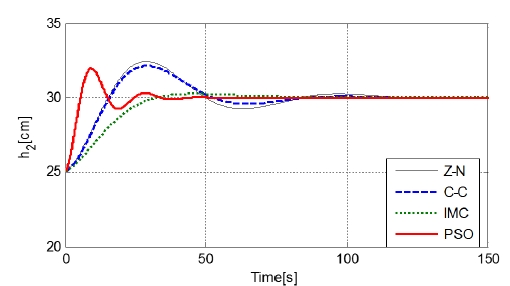
The PID parameter obtained by the PSO algorithm is compared to the Zeigler-Nichols tuning rule, the Cohen–Coon method and IMC.
PID controllers which are designed by the existing tuning methods are summarized in Table 2. Especially, for IMC, λ/L=0.25 was used [5]. The simulation results are as shown in the Figure 5.
Comparison of PID controller parameters
Closed-loop responses for set-point tracking with PID controllers
A comparison of time domain specifications peak overshoot, peak time, rise time (2%) and settling time are tabulated as given in Table 3.
Comparison of time domain specifications for set-point tracking
It is found very clearly that the PSO based PID controller drastically reduces the overshoot by a large value. Settling time, rise time and peak time have also improved. Although IMC method has the smallest peak amplitude, other performances have even worse results.
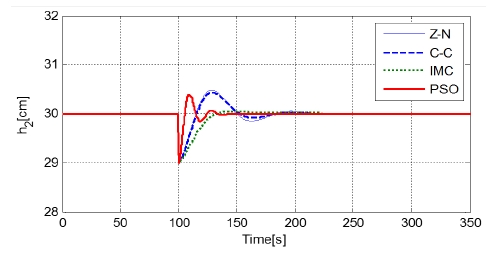
Next, we will consider the output responses with a static disturbance. Figure 6 shows the closed-loop response of the disturbance of magnitude -1.0 at 100 [s].
Closed-loop responses for disturbance rejection with PID controllers
A comparison of time domain specifications which are peak amplitude, peak time, recovery time (2% of disturbance amplitude) is tabulated as given in Table 4.
Comparison of time domain specifications for disturbance rejection
Although IMC method has the smallest peak amplitude, recovery time has even worse results.
Overall, the PSO based PID controller yields the best system recovery from load disturbance.
4.3 Performance Investigation
The PID controllers tuned by the PSO based method should not be compared only with their time domain responses but also with its performance index from the three major error criterion techniques of Integral of Absolute Error (IAE), Integral Time of Absolute Error (ITAE), Integral Square of Error (ISE).
Robustness of the controller is defined as its ability to tolerate a certain amount of change in the process parameters without causing the feedback system to go unstable. For the set-point tracking and disturbance rejection the comparison of performance index were done and are summarized in Table 5 and Table 6.
Comparison of performance index for set-point tracking
Comparison of performance index for disturbance rejection
From these values it is clearly visible that the error magnitude obtained for other conventional tuning rules is far too high as compared to the proposed tuning method based on PSO algorithm.
5. Conclusions
Particle Swarm algorithm is a robust, simple and very efficient optimization algorithm. In this paper, a systematic design method aiming at enhancing PID control for coupled tank processes is proposed. The paper shows to optimize the parameter of PID controller based on the PSO algorithm for given systems.
The research and simulation results show that the optimized PID controller parameters based on PSO algorithm can obtain the satisfactory control effects and the method is versatile, effective and feasible. It is shown practically that there is considerable improvement in the transient characteristics in terms of lesser rise time, peak time, settling time.
In case of disturbance rejection, the PSO based PID controller delivered an improved response to load disturbance, with improved recovery times and peak amplitude.
Using the PSO approach, global and local solutions could be simultaneously found for better tuning of the PID controller parameters.
However, proposed PSO optimization might not be the best tuning method in order to obtain the best parameter for PID controller. Further research is required to reduce overshoot or more improve the control performance of the system.
Acknowledgments
This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2014), held at Paradise Hotel, Busan, Korea on September 17-19, 2014.
References
-
A. Visioli, “Optimal tuning of PID controllers for integral and unstable processes”, IEE Proceedings on Control Theory and Applications, 148(2), p180-184, (2001).
[https://doi.org/10.1049/ip-cta:20010197]
-
M. Zhuang, and D. P. Atherton, “Automatic tuning of optimum PID controllers”, IEE Proceedings-D, 140(3), p216-224, (1993).
[https://doi.org/10.1049/ip-d.1993.0030]
- J. G. Ziegler, and N. B. Nichols, “Optimum setting for PID controllers”, Transactions of the American Society of Mechanical Engineers, 64, p759-768, (1942).
- G. H. Cohen, and G. A. Coon, “Theoretical investigation of retarded control”, Transactions of the American Society of Mechanical Engineers, 75, p827-834, (1953).
- M. Morari, and E. Zafiriou, Robust Process Control, Prentice-Hall, Englewood Cliffs, (1989).
- S. Jayasuriya, and J. W. Song, “On the synthesis of compensators for non overshooting step response”, Journal of Dynamic Systems, Measurement, and Control, 118(4), p757-763, (1996).
-
J. Kennedy, and R. Eberhart, “Particle swarm optimization”, IEEE International Conference on Neural Networks, 4, p1942-1948, (1995).
[https://doi.org/10.1109/ICNN.1995.488968]
- L. Zhou, Y. Fei, and W. You-bo, “PSO Algorithm based Online Self-Tuning of PID Controller”, International Conference on Computational Intelligence and Security, p128-132, (2007).
- B. Nagaraj, S. Subha, and B. Rampriya, “Tuning algorithms for PID controller using soft computing techniques”, International Journal of Computer Science and Network Security, 8(4), p278-281, (2008).
- S. Y. S Hussien, H. I. Jaafar, N. A. Selamat, F. S. Daud, and A. F. Z. Abidin, “PID control tuning via particle swarm optimization for coupled tank system”, International Journal of Soft Computing and Engineering, 4(2), p202-206, (2014).
-
Y. Shi, and R. Eberhart, “A modified particle swarm optimizer”, Proceedings of IEEE International Conference on Evolutionary Computation, p69-73, (1998).
[https://doi.org/10.1109/ICEC.1998.699146]
-
P. J. Angeline, “Using selection to improve particle swarm optimization”, Proceedings of IEEE International Conference on Evolutionary Computation, p84-89, (1998).
[https://doi.org/10.1109/ICEC.1998.699327]
-
H. Yoshida, K. Kawata, and Y. Fukuyama, “A particle swarm optimization for reactive power and voltage control considering voltage security assessment”, IEEE Transactions on Power Systems, 15(4), p1232-1239, (2000).
[https://doi.org/10.1109/59.898095]
-
R. C Eberhart, and Y. Shi, “Particle swarm optimization : developments, applications and resources”, Proceedings Congress on Evolutionary Computation, 1, p81-86, (2001).
[https://doi.org/10.1109/CEC.2001.934374]