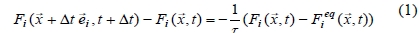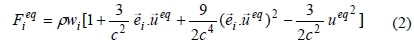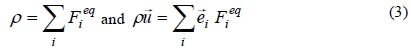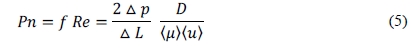LBM simulation on friction and mass flow analysis in a rough microchannel

1. Introduction

The surface roughness effect on flow resistance, heat-mass transfer in micro flows has great attention by many researchers due to the rapid advancement of micro electro mechanical system (MEMS), i.e. micromachining technology. The friction effect on surface roughness cannot be ignored, especially for gas flow in micro channels [1]. However, for flows on the macroscale, the surface roughness effect on the flow fiction is negligible for laminar flows with relative roughness less than 5% [2]. Actually, in microchannels, the main effects are rarefaction effects, essentially quantified by the Knudsen number Kn. According to the Rarefied Gas Dynamics (RGD), Knudsen number is defined as Kn=λ/L, where λ is the gas mean free path and L is the characteristic length of the flow system. It is investigated by many researchers [3]-[4] that surface roughness may have a significant impact on microchannel performances, both in terms of pressure drop and heat transfer. In their investigation, they used different approaches as well as different numerical schemes considering various types of rough surfaces with different relative roughness heights.

Recently, some investigations have been found via Lattice Boltzmann Method (LBM), neglecting compressibility effects. Actually, the LBM based on Boltzmann equation (BE), has attracted much attention as a novel alternative to traditional methods for numerically solving the Navier-Stokes (N-S) equation. Lattice gas models with an appropriate choice of the lattice symmetry in fact represent numerical solutions of the Navier-Stokes equations and therefore able to describe the hydrodynamics problems have been discussed by [5]-[6]. It is commonly recognized that the Lattice Boltzmann method (LBM) can faithfully be used to simulate the incompressible Navier-Stokes (N-S) equations with high accuracy and this lattice BGK (LBGK) model, the local equilibrium distribution has been chosen to recover the N–S macroscopic Equation [7]. Moreover, LBM provides a new effective way to study rarefied gas flow systems nowadays. The rarefaction effect is considered to be the most important factor that leads to different flow behaviors of rarefied gas dynamics in micro or nanoscale flows. Recently, some other authors [8]-[11] developed the method and studied micro flows in smooth microchannels by LBM. Up to now, few researchers have found in mirco gas flow to investigate the friction factor with surface roughness in MEMS devices. The roughness effect is one of the most important factors, especially in microchannels, for the friction factor in microfluidic systems. The roughness effect on friction factor in terms of Poiseuille number using the lattice Boltzmann method have been discussed by [12]-[14]. In their investigation, they considered the rectangular type of surface roughness elements that are distributed uniformly and symmetrically on the top and bottom walls.

In the present investigation, the authors would like to investigate the fluid flow, mass flow rate and friction factor with rarefaction effect as well as roughness height of circular shaped ribbed microchannel. This work is extended to previous study of the same authors [15]. In that work, the authors considered the roughness elements are on the middle of the channel, not throughout the channel. In order to avoid the effects of entrance and exit length ratios, the roughness elements are taken uniformly throughout the channel. A few investigations of this type of fluid flow problem using LBM are found in the literature, but to the author’s knowledge, the above mentioned problem has not been studied yet by this method. To analyze the flow variables in the slip flow regime, 0.01 < Kn < 0.10, with varying the relative roughness height from ε=0% to 10%, the friction coefficients in terms of Poiseuille number (Pn), mass flow and the velocity profiles in terms streamlines near the rough surface are discussed in the present study. It is seen that the pressure drop is significantly changed with roughness height and consequently all fluid flow characteristics changed with it. The fluid properties are taken to air properties. Throughout this study, the lattice units are considered and the computations were carried out with a code developed by the authors and written in FORTRAN language.

2. Formulation of the Problem

2.1 Mathematical Analysis

In the study of micro-flow system, it is very effective to apply the Lattice Boltzmann method instead of conventional CFD methods. To ensure this model satisfies the N-S equations for fluid, the Lattice-Boltzmann equation (LBE) with Bhatnagar-Gross-Krook collision operator can be written as Equation (1) [5].

The function F_i ( t) is the particle distribution function and F_i^eq is the discrete equilibrium distribution function with lattice velocity vectors 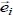[6]. The total number of discrete velocities on each node in D2Q9 model is 9 as shown in Table 1.

Table 1:

D2Q9 lattice velocities

Here c =Δx/Δt is called CFL umber, where Δx and Δt are the lattice unit of space and time. The relation between c and lattice speed of sound Cs can be expressed as C_s = c / 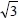. For two dimensional D2Q9 model, the equilibrium distribution function can be defined as Equation (2) [6]

where wi is the lattice weighting factors. The relaxation parameter, ω =1/τ, depends on the local macroscopic variables, ρ and . These variables should satisfy the following laws of conservation:

The above expressions describe the relations between the microscaled quantities define on the basis of lattice sizes and macroscaled physical quantities of flow such as the mass density and the velocity of the fluid.

2.2 Numerical Analysis and Boundary Conditions

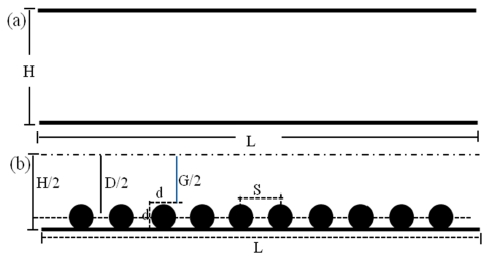
Consider a two dimensional microchannel with designed roughness and boundary conditions are shown in Figure 1.

Figure 1:

Schematic diagram of the problem: (a) smooth and (b) circular riblets microchannels

The surface roughness is modeled by a series of circular riblets both on the top and bottom walls boundary throughout the channel at a distance H=100μm from each other and the length L=220 μm. The relative roughness, ε=d/H, varies from 0% - 10%, where d is the roughness height or diameter of the circle. So, the hydraulic diameter D is changed with relative roughness height ε. The hydraulic diameter of the channel is calculated by D = (H+G)/2, G=H-2d, where G is the gap between pick position of two roughness elements at the top and bottom walls. S is the distance between two centres of riblets. It is considered at constant gap ratio, S^*=S/H=0.2 in this study. To investigate the roughness effect on flow characteristics, the friction coefficient f is defined as an average value either over a portion of rough section of the channel or over a single geometrically periodic roughness element [3]. In both cases f is defined as Equation (4):

where D is the hydraulic diameter, the variations ΔP and ΔL are computed between the inlet and outlet section, either the whole rough portion of the channel or of the single roughness element, <ρ> and <u> are the cross sectional average value. The product of the friction factor f and the Reynolds number Re is often referred to as the friction constant, called Poiseuille number, Pn= fRe. The Poiseuille number, Pn, is then written in terms of local Re as Equation (5):

Another important study of interest is the mass flow rate due to its applications in rough microchannel of gaseous flow. The mass flow rate is calculated from numerical results using the following expressions [13]:

It can be normalized by ρ₀UH², where ρ₀, U and H are characteristics density, velocity and height respectively. To apply the LBM in micro flow, a problem is arisen how to relate τ with K_n. The microscopic flows are usually characterized by the Knudsen number Kn defined as the ratio λ/H, where λ is the mean free path and H is the characteristics length

Where γ is the specific heat ratio, Ma is the Mach number and Re is the Reynolds number. Because of its micro-scale and high Knudsen number (Kn) flow corresponding to the slip flow regime, a special treatment should be considered for the relaxation time (τ). In previous lattice-BGK models, the relaxation time τ was chosen to be a constant during the computational procedure. This is applicable only for nearlyincompressible fluids. In micro-flows, the local density variation is still relatively small, but the total density changes, for instance the density difference between the inlet and outlet of a very long channel could be quite large. In order to account for this density variation and its effect on the kinematic viscosity ν, Nie et al. [17] proposed a new relaxation time τ’ in place of τ in Equation (1) in the following way:

Actually, the interaction between the gas molecules and the wall boundary are integrated into a single parameter, namely the tangential momentum accommodation coefficient (TMAC), σ. For D2Q9 lattice model, the particle distribution functions (F_i) on the wall, using the combined bounce rule, are introduced [11][12]. The Reynolds number is considered based on the hydraulic diameter of the channel and the maximum incoming flow velocity as well as the nature of fluid transport properties. In order to simulate a fully developed laminar channel flow upstream of the main cylinder, a parabolic velocity profile can be used at the inlet and outlet with a maximum velocity U at the midpoint of the channel. A series of computations carried out at a pressure ratio P_i/P_e =1.4, 1.3 and 1.2 for Kn= 0.02, 0.05 and 0.10 respectively, where P_i and P_e are the inlet and exit pressure respectively. In LBM, it cannot be used macroscopic variables directly, so the inlet and exit pressure conditions are used with the help of very simple equilibrium rules to the particle distribution functions. At the top and bottom wall, slip velocity boundary conditions are imposed by the standard bounce back treatment in order to eliminate the effect of compressibility [12].

3. Result and Discussions

Some key parameters are compared with other conventional benchmark and with experimental results. In order to verify our results, the friction factor in terms of Poiseuille number (Pn), defined by Equation (5), as shown in Figure 2.

Figure2:

Roughness effect on friction factor in terms of Poiseuille number (Pn) in a rough channel, rectangular shaped roughness geometry, for Kn=0.05

For verify our results with roughness geometry, it is considered the rectangular shaped roughness geometry with various relative roughness height, 0% ≤ ε ≤ 10%, for Knudsen number, Kn = 0.05. The validation of present simulation has been shown against numerical solution of Liu et al. [12]. A very good agreement is obtained between the present LBM simulation and bench mark as illustrated in Figure 2. And therefore, we would like to extend our work in different shaped of roughness geometry like circular shaped roughness geometry throughout the channel. The change of friction factor at various Knudsen number with relative roughness height in a smooth and rough microchannel with different roughness geometry are shown in Figure 3-5.

Figure 3:

Comparison of friction for smooth and rough channel with relative roughness height for Kn=0.05

Figure 4.

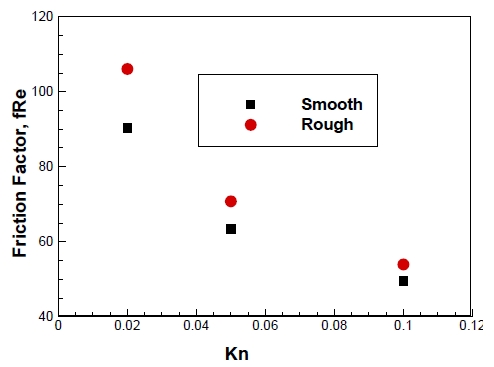
Comparison of friction for smooth and rough channel with various Kn at constant roughness height, ε=4%.

Figure 5:

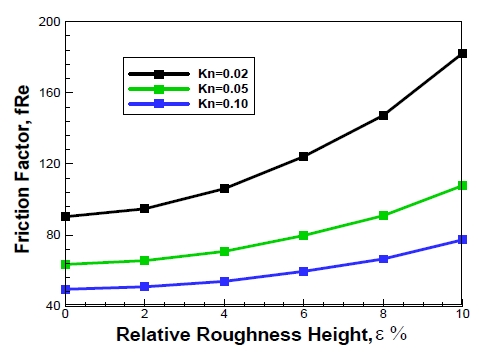
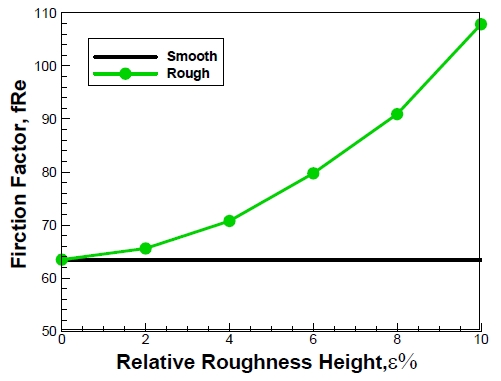
Effects of the surface roughness on the friction factor in terms of Poiseuille number for different Kn

The friction factor with relative roughness height for smooth channel (solid line), circular (●) riblets rough channels for constant Knudsen number, Kn=0.05 as shown in Figure 3. It is seen that the friction increases with roughness height and more friction is observed for rough channel. Moreover, it is seen from Figure 4 that the friction significantly decreases with increasing the rarefaction effects namely the Knudsen number within the slip flow region ranging from 0.01 to 0.10. This is obvious because of higher Knudsen number caused the higher velocity slip on the wall. Figure 5 shows the friction factor with roughness height for different Knudesn number, Kn=0.02, 0.05, and 0.10. It is seen the friction factor increased with relative roughness height and significantly decreased with increasing the Knudsen number. These phenomena are observed in rarefied gas micro flow in rough microchannels because of rarefaction effect adjacent to surfaces.

The near wall stream wise vortices for different Knudsen number, Kn=0.02, 0.05 and 0.10, are shown in Figure 6. Actually the streamlines in the rough channel is obtained from a post-process solution of the stream function equations. In order to avoid the entrance and exit length effects, only the mid two consequent roughness elements are considered to investigate the average roughness effects on fluid flow.

It is observed that the vortices are generated and driven by the relative roughness height as well as strongly influenced by the Knudsen number. With increasing the roughness height, the size and shape of vortices also increased and finally filled the gap between two neighboring roughness elements, not seen in the figure. Moreover, the strength of vortices also depends on Knudsen number as shown in Figure 6. The recirculation zone becomes larger for lower Knudsen number. This because for low Knudsen number, less slip velocity nears the wall and therefore more friction occurred and consequently increased the pressure drop. Therefore, it may conclude that the microchannel rough surfaces within the above limit of relative roughness height may cause the statistical change in the fluid flow behavior as well as friction factor for laminar flow.

Figure 6:

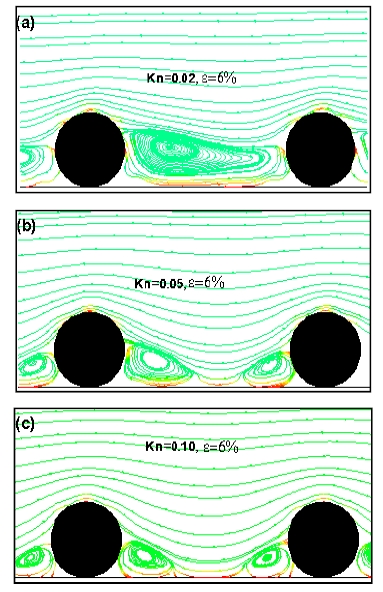
Streamlines near the rough surface of circular rough channel for Kn=0.05 with various relative roughness height.

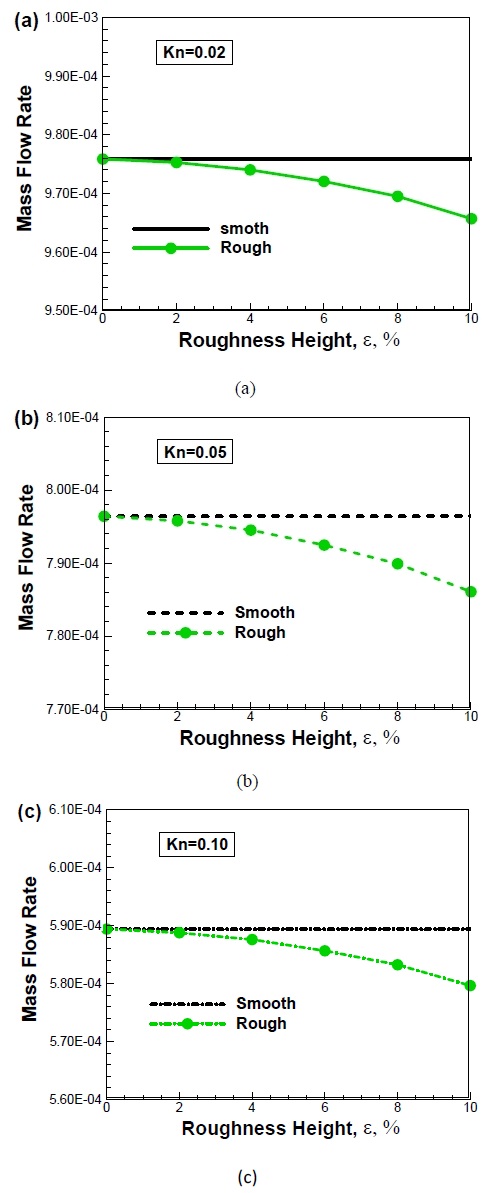
The effect of surface roughness height on the mass flow rate is illustrated in Figure 7 (a)-(c). It is seen from Figure 7 that the mass flow rate decreases with increasing the relative roughness height and the less flow is occurred compare to smooth channel at the slip flow regime. Moreover, it is seen that mass flow rate decrease linearly with relative roughness height but significantly decreased with increasing Knudsen number. It means that the more mass flows on low Kn compare to high Kn. This is obvious because it is seen from “Figure 6” that the surface roughness has a more significant effect on low Kn compare to high Kn. The similar phenomenon is studied by Chai et al. [13] in rectangular shaped roughed microchannel.

Figure 7:

Comparison of mass flow rate for smooth and rough channel at the slip flow regime: (a) Kn=0.02, (b) Kn=0.05 and (c) Kn=0.10

4. Conclusions

To investigate the mass flow rate, friction factor and flow variables of rarefied gas flow in a circular ribbed rough microchannel, the Lattice Boltzmann Method (LBM) is successfully applied. From this investigation, it may conclude that:

• Fluid flow behaviors near the rough surface are strongly influenced by the roughness height and Knudsen number in the slip flow region, 0.01 ≤ Kn ≤0.10, and consequently the mass flow rate and friction factor changed with them.

• Friction factor is increased with roughness height and decreased significantly with increasing Knudsen number.

• Mass flow rate decreased linearly with relative roughness height but decreased significantly with increasing Knudsen number.

• In all cases, it is seen that lower mass flow and higher friction are occurred in a rough microchannel compare to smooth channel.

• The size and shape of vortices become larger at low Knudsen number compare to high Knudsen number at the same conditions.

Acknowledgments

This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2014), held at Paradise Hotel, Busan, Korea on September 17-19, 2014.

References

• B. Y. Cao, M. Chen, and Z. Y. Guo, “Effect of surface roughness on gas flow in microchannels by molecular dynamics”, International Journal of Engineering Science, 44, p927-937, (2006). [https://doi.org/10.1016/j.ijengsci.2006.06.005]
• L. F. Moody, and N. J. Princeton, “Friction factor for pipe flow”, Transaction of the ASME, 66, p671-684, (1944).
• O. Rovenskaya, and G. Croce, “Numerical investigation of microflow over rough surfaces : Coupling approach”, Journal of Heat Transfer, 135, p101005-1-101005-8, (2013). [https://doi.org/10.1115/1.4024500]
• M. H. Khadem, M. Shams, and S. Hossainpour, “Effects of rarefaction and compressibility on fluid flow at slip flow regime by direct simulation of roughness”, International Journal of Aerospace and Mechanical Engineering, 3(4), p204-210, (2009).
• G. R. McNamara, G. Zanetti, “Use of the Boltzmann equation to simulate lattice-gas automata”, Physical Review Letters, 61(20), p2332-2335, (1988). [https://doi.org/10.1103/PhysRevLett.61.2332]
• X. Wei, K. Mueller, and A. E. Kaufman, “The lattice Boltzmann method for simulating gaseous Phenomena”, IEEE Transactions on Visualization and computers Graphics, 10(2), p164-176, (2004).
• H. Chen, S. Chen, and W. H. Matthaeus, “Recovery of the navier-stokes equations using a lattice-gas Boltzmann method”, Physical Review A, 45(8), p5339-5342, (1992). [https://doi.org/10.1103/PhysRevA.45.R5339]
• S. Chen, and Z. Tian, “Simulation of microchannel flow using the lattice Boltzmann method”, Physica A, 388, p4803-4810, (2009). [https://doi.org/10.1016/j.physa.2009.08.015]
• X. D. Niu, C. Shu, and Y. T. Chew, “A thermal lattice Boltzmann model with diffuse scattereing boundary condition for micro thermal flows”, Computers and Fluid, 36, p273-281, (2007). [https://doi.org/10.1016/j.compfluid.2005.11.007]
• Y. H. Zhang, R. S. Qin, R. W. Barber, and D. R. Emerson, “Gas flow in microchannels - A Lattice Boltzmann Method approach”, Journal of Statistical Physics, 121(1/2), p257-267, (2005). [https://doi.org/10.1007/s10955-005-8416-9]
• S. H. Kim, and H. Pitsch, “Slip velocity and Knudsen layer in the lattice Boltzmann method for microscale flows”, Physical review E, 77, p026704-1-026704-12, (2008). [https://doi.org/10.1103/PhysRevE.77.026704]
• C. Liu, J. Yang, and Y. Ni, “A multiplicative decomposition of Poiseuille number on rarefaction and roughness by lattice Boltzmann simulation”, Computers and Mathematics with Applications, 61, p3528-3536, (2011).
• Z. Chai, Z. Guo, L. Zheng, and B. Shi, “Lattice Boltzmann simulation of surface roughness effect on gaseous flow in a microchannel”, Journal of Applied Physics, 104, p014902-1-014902-8, (2008). [https://doi.org/10.1063/1.2949273]
• L. Chao-Feng, and N. Yu-Shan, “The effect of surface roughness on rarefied gas flow by lattice Boltzmann method”, Chinese Physics B, 17(12), p4554-4561, (2008).
• M. A. Taher, H.D. Kim, C.S. Kang, and Y. W. Lee, “Friction and flow analysis of square and circular riblets rough microchannels using LBM”, Proceedings of the 5^th Asian Workshop on Thermphysics and Fluid Science, (KA-27), (2014).