Analysis of effect of coherent and incoherent components on RCS of chaff cloud
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Chaff is the most basic electromagnetic countermeasure against radars. However, electromagnetic analysis of chaff clouds is very difficult because individual chaff has an electrically short and chaff cloud consisting of an extremely large number of chaffs. In this study, we estimated the radar cross section (RCS) of chaff clouds composed of 0.5λ, 0.75λ, and 1λ-long chaff fibers using the effective medium method (EMM) and analyzed the effect of coherent and incoherent RCSs on the average RCS of chaff clouds. The RCS obtained using the EMM was verified by comparing it with the results obtained using the method of moments applying the Monte Carlo method. At low densities, the RCS levels of chaff clouds, composed of 0.5λ-long chaff fibers and chaff clouds composed of 1λ-long chaff fibers, were almost in agreement. However, as the density increased, the RCS levels of chaff clouds composed of 1λ-long chaffs became much larger. Additionally, the chaff cloud composed of 0.75λ-long chaffs showed a lower RCS level than other chaff clouds because resonance did not occur. However, the RCS of the chaff cloud was mainly determined by the incoherent component as opposed to the coherent component, and the coherent RCS was negligible to a much lower level than the incoherent RCS.
Keywords:
Chaff, Coherent RCS, Effective medium method (EMM), Incoherent RCS, RCS1. Introduction
The chaff is a metallic fiberglass or foil, and it has electromagnetic characteristics that resonate and disturb when it has a length of half the wavelength of the radar operating frequency [1]. Given these characteristics, chaff is widely used as the most basic electromagnetic countermeasure for radar detection. However, a single chaff cartridge is composed of as few as thousands or as many as millions of chaff fibers, and when used, numerous chaff fibers are scattered in the air to form a chaff cloud [2]. As large number of chaff fibers are scattered to form a chaff cloud, the coupling between the chaffs must also be considered when calculating the radar cross-section (RCS) of the chaff cloud. To accurately consider the coupling between chaffs, low-frequency numerical methods, such as the method of moments (MoM) and finite element method (FEM), should be used. Although these low-frequency numerical methods provide high accuracy, they require considerable computing resources and computation time. Therefore, in practice, only hundreds to thousands of chaffs can be analyzed. Owing to the limitation of low-frequency methods, in an early study, the RCS of chaff clouds was simply obtained by multiplying the average RCS of a single chaff to the number of chaffs [3]-[5]. However, only approximate RCS level information is provided because the coupling between the chaffs, orientation, and location distributions are not considered. Recently, studies have been conducted to dramatically reduce the amount of computation and computation time using various approximation techniques by considering the coupling between chaffs and information on orientation and location distributions. Marcus [6] considered the coupling between chaffs as an equivalent conductor with the same conductivity as the slab by dividing the chaff clouds into very thin slabs and assuming a high density of chaff clouds. Conversely, Alvarez [7] considered the coupling between slabs using a transmission line approximation. In a manner similar to [6], Seo [8] considered the chaff cloud as an equivalent conductor and considered coupling, but divided it into cubes as opposed to slabs using an octree algorithm. Additionally, it is possible to calculate the RCS for chaff clouds with various orientation distributions [8]. Y. Zuo [9] simulated the RCS of the chaff cloud by considering coupling using vector radiative transfer (VRT), which is used when particles with arbitrary shapes are randomly distributed in the medium [9].
In this study, the RCS of the chaff cloud was obtained using the effective medium method (EMM) mentioned in [8], and it was verified by comparing it with the MoM, which is a conventional numerical method with high accuracy. Additionally, the characteristics of the coherent and incoherent RCS of a chaff cloud and their effect on the average RCS of the chaff cloud were analyzed.
2. Effective Medium Method for RCS Analysis of Chaff Cloud
EMM is a method for calculating the electromagnetic characteristics of the entire scattering body by replacing the chaff cloud formed by the dispersion of the chaffs with an effective medium.
2.1 Effective Medium Model [10]
The effective permittivity (εeff) of a chaff cloud with a random distribution is as follows:
| (1) |
where ε0 denotes the permittivity in free space, η0 denotes the characteristic impedance in free space, ρ denotes the density of the chaff cloud, λ denotes the wavelength, l denotes the length of the chaff, and s denotes nondimensional parameter of effective permittivity. Furthermore, denotes the effective average current of the chaff per unit wavelength and is expressed as follows:
| (2) |
where ̇ (θ,ϕ) denotes the scattered field component in the -x direction when a z-polarized plane wave is incident on the chaff as shown in Figure 1. This can be calculated as follows:
| (3) |
where (θ,ϕ) denotes the orientation vector of chaff in the spherical coordinate system. Equation (2) assumes that chaff is randomly oriented in all directions.
However, if there are many distributions in the specific orientation of the chaffs, the probability density function (pdf) of the orientation distribution is set as the weighting function W and weight is applied to the specific orientation by using the weighted average [11]. The weighted average is as follows:
| (4) |
Based on these procedures, the chaff cloud can be replaced by an effective medium with the effective permittivity of the chaff cloud considering the orientation distribution of the chaffs.
2.2 Coherent RCS
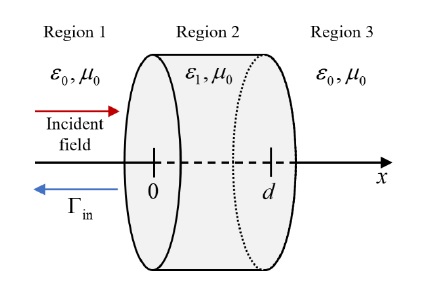
The reason for calculating the number of chaffs by replacing them with an effective medium with effective permittivity involves obtaining a coherent RCS. A coherent RCS is the average RCS. Specifically, the coherent RCS is determined by the overall shape of the effective medium and can be calculated from the reflection coefficient at the effective medium interface as shown in Figure 2.
The input reflection coefficient of the slab structure shown in Figure 2 is as follows:
| (5) |
where Γ12 and Γ23 denote the interference reflection coefficients between Regions 1 and 2 and between Regions 2 and 3, respectively, and γ2 denotes the complex propagation constant in Region 2.
The field scattered by the effective medium is a coherent scattered field, and the coherent RCS can be obtained as ollows:
| (6) |
where A denotes the area of the effective medium.
2.3 Incoherent RCS [12]
When a large number of scatterers exist, there are not only coherent scattered fields but also incoherent scattered fields, and the incoherent scattered fields are changed by a spatial change in the scatterers. Therefore, the incoherent field represents fluctuations in the scattered field. Specifically, as the number of scatterers increase and similarity between the scatterers decrease, the incoherent scattered field component increases. Therefore, even in the field scattered by the chaff with the same density, as the thickness of the effective medium increases, the coherent component decreases and incoherent component increases. To calculate the incoherent RCS of the effective medium, the incoherent scattered field can be obtained by ignoring the mutual coupling between the chaffs, calculating only the scattered field by the chaffs, and considering only the location of the scatterers. The incoherent scattered field of the effective medium is as follows:
| (7) |
where μ0 denotes the permeability in free space, J denotes the volume current density, R denotes the distance between the target and observation point, k0 and k1 denote the wavenumber of the free space and effective medium, respectively, and A denotes the cross-section of the effective medium. Using this scattered field, the incoherent RCS can be obtained as follows:
| (8) |
Finally, the RCS of the effective medium is obtained by adding the coherent RCS and incoherent RCS as follows:
| (9) |
3. RCS of Chaff Cloud and Analysis
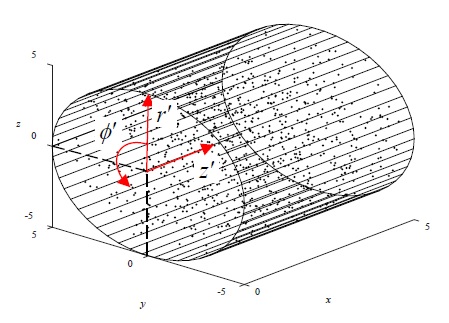
In our simulation and analysis, we assumed that the volume of the chaff cloud was cylindrical with a radius of 5λ and height of 5λ. To obtain the RCS of the effective medium, a cross-section of the effective medium was used. Therefore, not only cylinders with a circular cross-section, but also cubes with a rectangular cross-section can be used. However, in conventional studies, a cylinder with a circular cross-sectional area is commonly adopted because the shape of the chaff cloud is formed in the shape of a sphere or ellipsoid [8][13]-[15]. The EMM has a limitation wherein it can be applied only when the densities of the chaff clouds in the volume are all the same. If the densities of the chaff cloud in the volume are not the same, then EMM is applied by dividing the chaff cloud to maintain the same volume density. In this study, the chaff cloud, which is the simplest case, is set to exhibit random orientation and location distributions, and all densities within the volume are set to be the same. Therefore, the probability density functions of r', ϕ', z' are defined as follows:
| (10a) |
| (10b) |
| (10c) |
The locations of chaffs randomly obtained through the location distribution function are transformed into the Cartesian coordinate system using the following transformation.
| (11a) |
| (11b) |
| (11c) |
The orientation distribution of the chaffs was also set as randomly distributed in all orientations as the simplest case. In this case, the probability density functions θ and ϕ are as follows:
| (16) |
| (17) |
The number of chains in the volume was set from 100 to 900, and simulations were performed for densities of approximately 0.25 to 2.30 N/λ3. When the MoM is used, the RCS is obtained by increasing the number of chaffs by 200, from 100 to 900, because it requires considerable computing resources and computation time to obtain the RCS [16]. The EMM requires the chaff density and orientation distribution for the RCS calculation; however, the exact orientation and location of all chaff fibers must be determined for the MoM for verification. The 900 chaffs exhibit a chaff cloud volume and random location distribution as shown in Figure 3.
3.1 Chaff Cloud Composed of 0.5λ-long Chaffs
The length of the chaff, composing the chaff cloud, was set to 0.5λ. When simulating the RCS of 900 chaffs using MoM, the calculation time required for one simulation was approximately 95 min. When using the EMM, a total of 1.7 s were required. Additionally, the MoM requires a large amount of calculation time by repeating the analysis 20 times for each case using the Monte Carlo method.
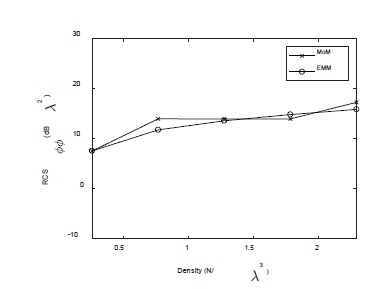
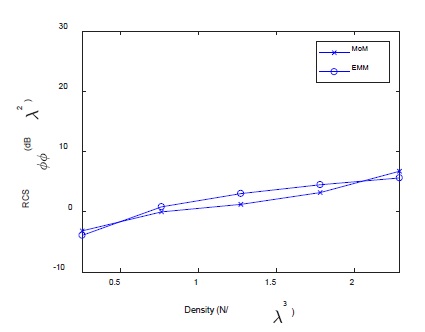
As shown in Figure 4, there is a small difference of 2 dB between the results of EMM and MoM. If the number of iterations in the Monte Carlo method increases, then the difference is expected to decrease.
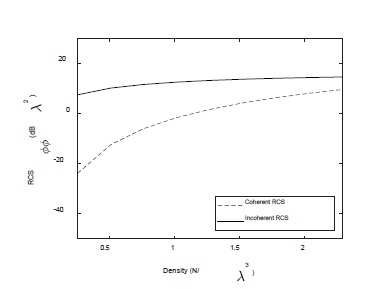
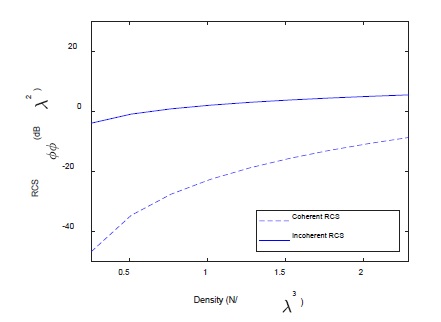
The RCS obtained by EMM can be separated into coherent and incoherent RCS as shown in Figure 5. The level of coherent RCS increases as the density increases. Even at a density of 2.3 N/λ3, there is a 5-dB difference between the two components, and the coherent RCS is relatively negligible. Additionally, the incoherent RCS level increases as the density increases, but it can be shown that it gradually becomes saturated as the density increases. At a density of 2.3 N/λ3, the difference between RCSϕϕ and incoherent RCS is very small (0.5 dB), and accordingly, it can be confirmed that the effect of coherent RCS is very small.
3.2 Chaff Cloud Composed of 0.75λ-long Chaffs
A chaff cloud composed of 0.75λ-long chaff fibers is considered. When the RCS of 900 chaffs is simulated using the MoM, the calculation time required for a single iteration is approximately 185 min, and when the EMM is used, a total of 2.9 s are required.
The results of the EMM and MoM are plotted in Figure 6, and the difference between the results of the two methods is small within 1.8 dB. Given that a chaff fiber with a length of 0.7λ does not resonate at the corresponding frequency, the average RCS at a density of 2.3 N/λ3 is about 5.6 dB, which is 10 dB lower than that of a chaff cloud composed of 0.5λ-long chaffs where resonance occurs.
As shown in Figure 7, the difference between coherent RCS and incoherent RCS even at a density of 2.3 N/λ3 is 14 dB. Given that resonance does not occur in 0.75λ-long chaff, the RCS level is 9 dB higher than that of 0.5λ-long chaffs. Moreover, the difference between RCSϕϕ and incoherent RCS at the density of 2.3 N/λ3 is very small, i.e., 0.1 dB. Hence, coherent RCS is negligible.
3.3 Chaff Cloud Composed of 1λ-long Chaffs
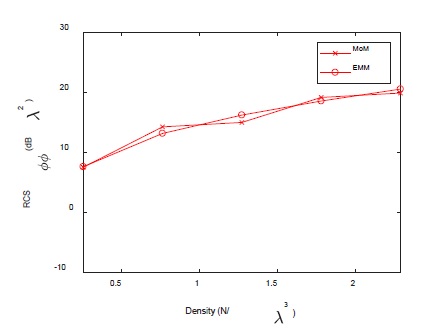
The length of the chaff composing the chaff cloud was set to 1λ. In the case of simulating the RCS of 900 chaffs using the MoM, the calculation time required for a single iteration was approximately 266 min; in the case of using the EMM, a total of 3.8 s were required. As shown in Figure 8, there is a small difference of 1.2 dB between the RCSs of the MoM and EMM. At a density of 0.25 N/λ3, the difference from the chaff cloud with a 0.5λ-long chaff was 0.1 dB, which was small. However, as the density increased, the difference with the RCSϕϕ of the chaff cloud, composed of 0.5λ-long chaffs, increased, resulting in a difference of 4.7 dB at a density of 2.3 N/λ3.
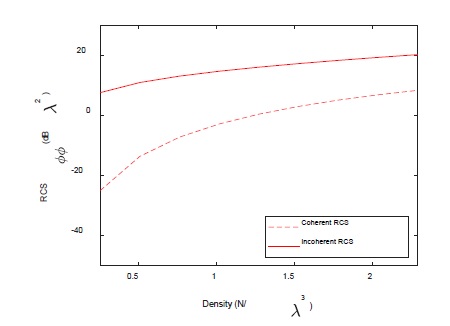
Given that resonance occurs in 1λ-long chaff, as shown in Figure 9, the difference between the coherent RCS and incoherent RCS at a density of 2.3 N/λ3 is 11.9 dB, which is 6.9 dB higher than that of the 0.5λ-long chaffs. When comparing the coherent RCS with the incoherent RCS, the coherent RCS is at a similar level within 1.2 dB when compared to the chaff cloud composed of 0.5λ-long chaffs. However, the incoherent RCS is within 5.6 dB, it is less than 5.6 dB, and the effect of the coherent RCS is smaller and effect of incoherent RCS is higher. Additionally, at a density of 2.3 N/λ3, the difference between RCSϕϕ and incoherent RCS is very small and corresponds to 0.2 dB, and the coherent RCS is negligible.
Based on these results, as the number of chaffs increases and the chaffs resonate with an odd multiple of the half-wavelength of the radar operating frequency, the effect of incoherent RCS becomes greater than that of coherent RCS. As the number of scatterers increases, the incoherent scattered fields owing to various orientations and locations increase. Additionally, it can be shown that this occurs because individual chaffs generate more scattered fields near the resonance frequency. Furthermore, the larger deviation of the scattered field between scatterers owing to the orientation distribution of the chaff is due to the similarity between the scatterers.
4. Conclusion
In this study, the RCSs of chaff clouds composed of chaffs with lengths of 0.5, 0.75, and 1λ were simulated using the EMM. The RCSs obtained using the EMM were verified by comparing them with the results obtained using the MoM by applying the Monte-Carlo method. In the case of chaff clouds composed of chaffs with resonant length, RCSs exhibited similar levels at low density, but as the density increased, the incoherent RCS of chaff clouds composed of long chaffs increased. Therefore, the effect of coherent RCS was small and had a higher level. Additionally, the RCSs of the chaff clouds obtained using EMM were mainly determined by the incoherent RCS. At a density of upto 2.3 N/λ3, the coherent RCS increased as the density increased, but was negligible at a very small level. If the density is higher than 2.3 N/λ3, then the effect of coherent RCS increases and cannot be considered as negligible. However, a density higher than that can be observed immediately after the chaff is spread. In this case, RCS analysis is not difficult because the volume of the chaff cloud is small and can be treated as a single conductor.
Conventional studies have mostly focused on calculating the coherent RCS as opposed to the incoherent RCS to consider the coupling. However, even at a density of 2.3 N/λ3, with the highest coherent RCS level, the coherent RCSs were 5 dB, 14 dB, and 11.9 dB lower than their incoherent RCSs of 0.5-, 0.75-, and 1.0λ-long chaffs, respectively. Therefore, coherent RCS has a very small effect on the average RCS of a chaff cloud when compared to incoherent RCS. If future studies are focused on incoherent RCS calculations, then a more accurate and faster analysis of chaff clouds is possible.
Acknowledgments
This work was supported by Theater Defense Research Center funded by Defense Acquisition Program Administration under Grant UD200043CD.
Author Contributions
Conceptualization, D. -W. Seo; Methodology, D. -Y. Lee; Software, J. -S. Kim; Validation, D. -Y. Lee; Formal Analysis, D. -Y. Lee; Investigation, D. -Y. Lee and D. -W. Seo; Resources, D. -Y. Lee; Data Curation, D. -Y. Lee; Writing—Original Draft Preparation, D. -W. Seo; Writing—Review & Editing, D. -W. Seo; Visualization, D. -W. Seo; Supervision, D. -W. Seo; Project Administration, D. -W. Seo; Funding Acquisition, D. -W. Seo.
References
-
H. Wang, and et al., “Mono-static RCS of Chaff Simulated Based on MoM,” Proceedings of the 2019 IOP Conference Series: Materials Science and Engineering, vol. 563, no. 5, 2019.
[https://doi.org/10.1088/1757-899X/563/5/052084]

- E. F. Knott, D. J. Lewinski, and S. D. Hunt, Chaff Theoretical/Analytical Characterization and Validation Program, ADA105893, USA, 1981. [Online]. Available: https://apps.dtic.mil/sti/pdfs/ADA105893.pdf, .
- J. M. Madewell, “Mitigating the effects of chaff in ballistic missile defense,” Proceedings of the 2003 IEEE Radar Conference, pp. 19-22, 2003.
- D. Della Ducata, G. Foglia, D. Pistoia, and A. Sindico, “A comprehensive model for chaff characterization,” Proceedings of the 6th European Radar Conference, pp. 485-488, 2009.
-
G. Zhu, L. Man, Y. Chen, and H. Yin, “Approach of electromagnetic modeling for chaff clouds formed by exploding,” Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), pp. 1-3, 2018.
[https://doi.org/10.1109/COMPEM.2018.8496696]

-
S. W. Marcus, “A model for EM propagation through dense clouds of wire dipoles,” Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, pp. 735-738, 2006.
[https://doi.org/10.1109/APS.2006.1710631]

-
J. Alvarez and D. E. Bocanegra, “Discrete electromagnetic model for the evaluation of wideband bistatic scattering responses and statics of chaff clouds,” IEEE Transactions on Antennas and Propagation, vol. 68, no. 8, pp. 6256-6264, 2020.
[https://doi.org/10.1109/TAP.2020.2985771]

-
D. W. Seo, H. -J. Nam, O. -J. Kwon, and N. H. Myung, “Dynamic RCS estimation of chaff clouds,” IEEE Transactions on Aerospace and Electronic Systems, vol. 48, no. 3, pp. 2114-2127, 2012.
[https://doi.org/10.1109/TAES.2012.6237582]

-
Y. Zuo, L. Guo, W. Liu, and S. Liu, “A bistatic scattering evaluation method of the chaff cloud in airflow based on VRT,” IEEE Transactions on Antennas and Propagation, vol. 69, no. 12, pp. 8698-8710, 2021.
[https://doi.org/10.1109/TAP.2021.3090813]

-
D. W. Seo, J. H. Yoo, K. I. Kwon, and N. H. Myung, “Generalized equivalent conductor method for a chaff cloud with an arbitrary orientation distribution,” Progress In Electromagnetics Research, vol. 105, pp. 333-346, 2010.
[https://doi.org/10.2528/PIER10051202]

-
D. W. Seo, H. J. Kim, K. U. Bae, and N. H. Myung, “The effect of fiber orientation distribution on the effective permittivity of fiber composite materials,” Journal of Electromagnetic Waves and Applications, vol. 24, no. 17-18, pp. 2419-2430, 2012.
[https://doi.org/10.1163/156939310793675835]

-
D. W. Seo, J. H. Lee, and H. Lee, “Estimation of incoherent scattered field by multiple scatterers in random media,” ETRI Journal, vol. 38, no. 1, pp. 141-148, 2016.
[https://doi.org/10.4218/etrij.16.0114.1237]

-
C. Gang, S. Longfei, M. Jiazhi, and L. Jian, “Identification of chaff interference based on polarization parameter measurement,” Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments, pp. 392-396, 2017.
[https://doi.org/10.1109/ICEMI.2017.8265829]

-
J. Alvarez and D. E. Bocanegra, “Discrete electromagnetic model for the evaluation of wideband bistatic scattering responses and statistics of chaff clouds,” IEEE Transactions on Antennas and Propagation, vol. 68, no. 8, pp. 6256-6264, 2020.
[https://doi.org/10.1109/TAP.2020.2985771]

-
X. Hong-Jie, L. Jian-Bing, X. Zhong-Fu, and W. Tao, “Analysis of wideband characteristics and jamming technology of chaff cloud,” Proceedings of 2014 3rd Asia-Pacific Conference on Antennas and Propagation, pp. 1053-1057, 2014.
[https://doi.org/10.1109/APCAP.2014.6992689]

-
D. W. Seo, J. H. Yoo, K. I. Kwon, and N. H. Myung, “A hybrid method for computing the RCS of wire scatterers with an arbitrary orientation,” Progress In Electromagnetics Research B, vol. 23, pp. 55-68, 2010.
[https://doi.org/10.2528/PIERB10060803]