Matching performance of single channel pump by the combination of various cross-sectional shapes of impeller outlet and volute casing
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A single-channel pump is a sewage pump with a unique non-clog impeller. This pump is employed in drainage, wastewater control systems, agriculture, and aquaculture. Particularly, with a free passage impeller, a single-channel pump can transfer live fish, eel, and shrimp without clogging and damage. The flow passage shape of a single-channel pump is vital for live fish transfer. In this study, the matching performance of a single-channel pump was evaluated using various cross-sectional shapes of the impeller outlet and volute casing. The pump performance, internal flow characteristics, and suction performance were compared to determine the best combination of the impeller outlet and volute casing cross-sectional shapes. The results revealed that the circular cross-sectional shape of the impeller outlet with the circular cross-sectional shape of the volute casing showed better pump hydraulic and suction performances.
Keywords:
Single channel pump, Matching performance, Hydraulic performance, Suction performance, Cross sectional shape, Impeller outlet, Volute casing1. Introduction
Single-channel pumps are widely employed in sewage, fish, eel, shrimp, fruit, and vegetable transfers. The single-channel pump impeller has a free passage from the impeller suction to discharge, which improves the solid handling capability [1]. Hence, a single-channel pump can be employed for fruit or live fish transfer without causing clogging or damage. Therefore, the flow passage shape of a single-channel pump plays a significant role in live fish transfer and the pump performance.
The design method and optimization of single-channel pumps for wastewater treatment and the evaluation of the operating vibration of the impeller-volute interaction were studied by Kim et al. [2]. Guo et al. [3] evaluated the effect of the impeller blade thickness on the pump performance and internal flow characteristics of a single-channel pump model. Wu et al. [4] predicted the tendency of the single-channel pump performance using various turbulence models. Keays et al. [5] used numerical and experimental methods to study the power loss and poor efficiency of a single-blade wastewater pump caused by the complicated flow behind the trailing edge. The FSI solution strategy for the fluid-structure system in a single-blade centrifugal pump was proposed by Pei et al. [6] to reduce the pressure fluctuation and increase the reliability of the pump. The trailing edge modifications of centrifugal wastewater pump impellers were studied by Litfin et al. [7] using numerical and experimental methods.
The optimal shape design of the single-channel pump impeller and volute casing shapes is difficult to find in literature. Therefore, this study aimed to evaluate the matching performance of a single-channel pump using various cross-sections of the impeller outlet and volute casing. Accordingly, the hydraulic pump performance, internal flow characteristics, and suction performance of single-channel pump models were examined using computational fluid dynamics (CFD) analysis.
2. Design of Single-Channel Pump
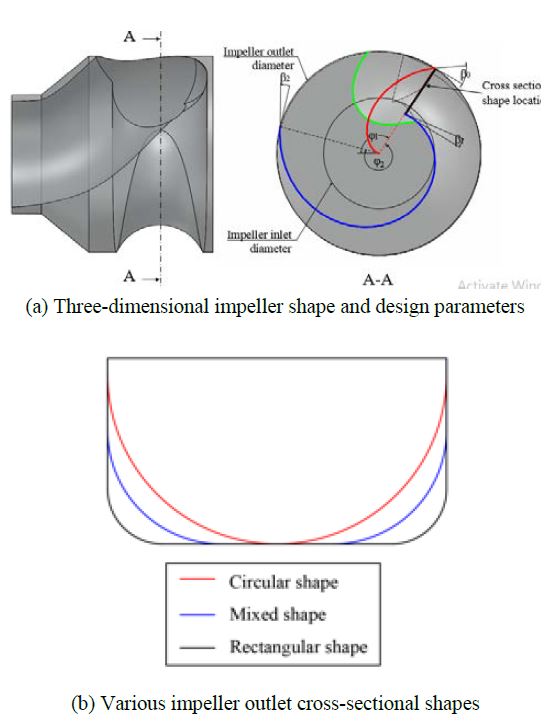
The design specifications of the single-channel pump model are presented in Table 1. The three-dimensional and cross-sectional shapes of the outlet of the impeller model are shown in Figure 1. The design parameters of the single-channel pump impeller were calculated based on the study results [1] as listed in Table 2. The design parameters for the single-channel pump were D1, D2, β0, β1 and β2. The detailed design method of a single-channel pump impeller has been presented in previous studies [1][3].
Stepanoff’s design method [8] was adopted for the volute casing design, as shown in Figure 2. The cross-sectional area distribution of the volute casing was linearly proportional to the theta angle, as shown in Figure 2(b). However, the centrifugal pump impeller and casing shapes were determined by matching the BEP [9]. The design method for a single-channel pump cross-sectional passage shape is unclear and difficult to find in literature. As a preliminary study, various impeller outlet cross-sectional shapes were selected to evaluate the pump-matching performance. The design scheme of the single-channel pump impeller outlet is shown in Figure 1(b). Similarly, the cross-sectional shapes of the volute casing were circular, mixed, and rectangular shapes that are adopted, as shown in Figure 2(c). Single-channel pump models were generated according to the impeller outlet and volute casing cross-sectional shapes listed in Table 3.
3. Numerical Method
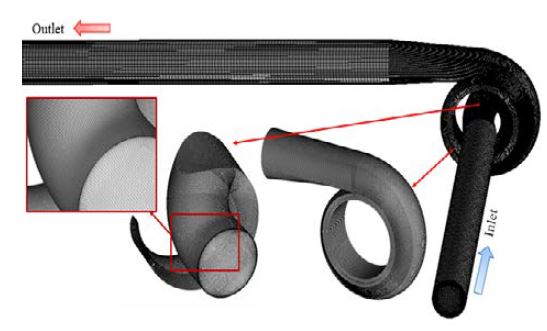
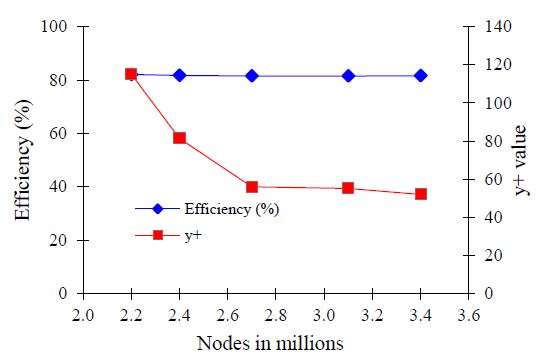
CFD analysis was performed to evaluate the pump hydraulic and suction performances of the single-channel pump models. A commercial CFD analysis code, ANSYS CFX 18.1 [10], was employed for all the numerical simulations. Figure 3 illustrates the hexahedral numerical grids of the impeller and volute casing fluid domains of the single-channel pump model for case CC. The hexahedral mesh was generated using ANSYS ICEM 18.1 [11]. A mesh dependence test for the single-channel pump model of case CC was implemented, as shown in Figure 4. The pump efficiency and maximum y+ value were calculated using Equations (1) and (2), which were used to perform the mesh dependency test. According to the mesh dependency test, 2.8 million nodes were selected to conduct the CFD analysis for the single-channel pump models.
| (1) |
| (2) |
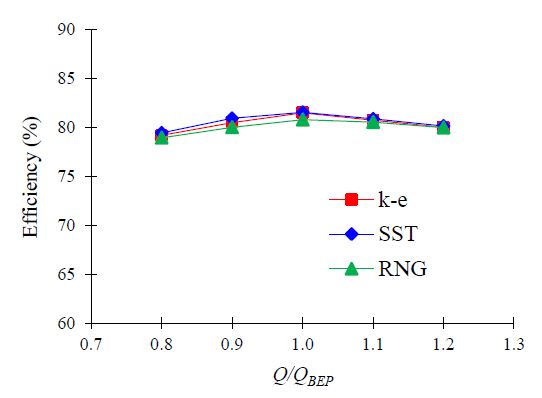
The turbulence models of k–ɛ, RNG k–ɛ, and shear stress transport (SST) were employed to conduct the turbulence model dependence test, as shown in Figure 5. All the turbulence models were compared with the pump hydraulic performance curves. The shear stress transport (SST) turbulence model is preferable for evaluating the complicated flow field in fluid machinery and estimating both flow separation and swirl flow on the wall [12].
The numerical methods and boundary conditions for steady-state analysis are listed in Table 4. The Rayleigh-Plesset cavitation model was adopted for cavitation flow simulation in this study. Water and water vapor were used as the working fluids at 25 °C. The total pressure and mass flow rate were the inlet and outlet boundaries of the single-channel pump, respectively. A frozen rotor was used to create the interface between the fixed and rotating domains.
4. Results and Discussion
4.1. Pump hydraulic performance
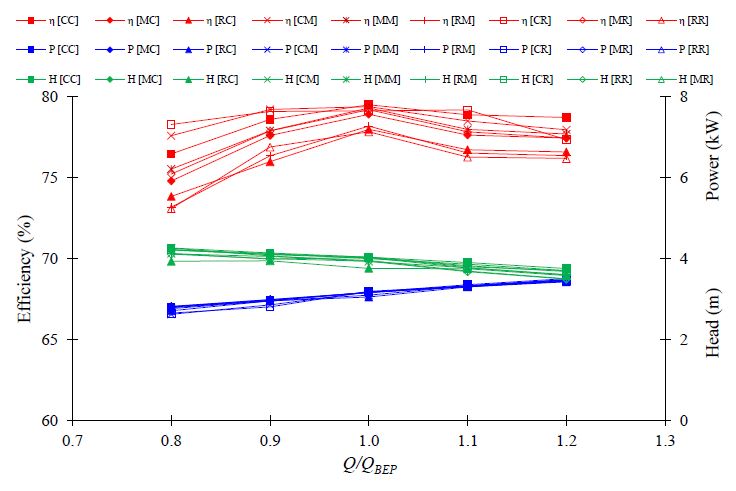
The pump-matching performance was evaluated based on the cross-sectional shapes of the impeller outlet and volute casing. Nine single-channel pump models with three cross-sectional shapes of the impeller outlet and three cross-sectional shapes of the volute casing were employed under non-cavitation conditions for the CFD analysis. Figure 6 illustrates the pump-matching hydraulic performance curves for various cross-sectional shapes of the impeller outlet and volute casing models. The results show that the efficiency of the circular cross-sectional impeller outlet with the circular cross-sectional volute model (Case CC) was higher than that of the other models for the entire flow rate range. The various impeller outlet and volute casing cross-sectional shapes showed differences in the pump hydraulic performance. All single-channel model designs were acceptable because the design point matched the best efficiency point. Therefore, it was concluded that the cross-sectional shape of the impeller outlet had a more significant influence on the pump hydraulic performance than that of the volute casing. Case CC exhibited a better hydraulic performance than the other cases.
4.2. Internal flow characteristics
The matching loss analysis of the impeller and volute casing is defined by Equations (3) and (4).
| (3) |
| (4) |
Figure 7 presents the matching loss analysis results of the impeller and volute casing passages based on various cross-sectional shapes of the impeller outlet and volute casing at the design point. In the impeller domain, the hydraulic loss of the circular cross-sectional shape of the impeller showed a relatively lower value, regardless of the volute casing type (Cases CC, CM, and CR). However, the rectangular cross-sectional shape of the impeller shows a relatively higher loss for all volute casing types (RC, RM, and RR). In the volute casing domain, the hydraulic loss changes noticeably in all combination cases owing to the various cross-sectional shapes of the impeller outlet and volute casing.
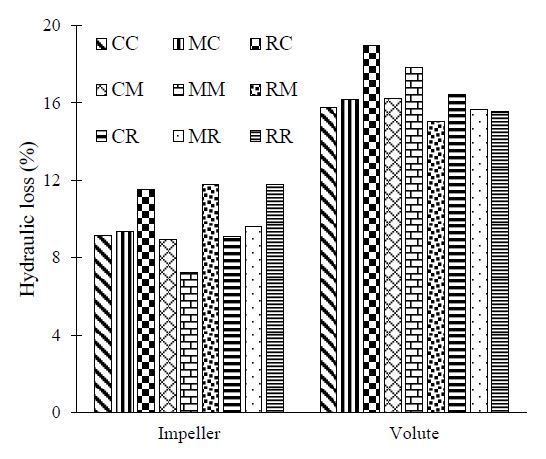
Matching loss analysis of the impeller and volute by the various impeller out and volute casing cross-sectional shapes at the design point
Figure 8 shows the variation in the velocity streamlines in the volute flow passages with the mixed cross-sectional impeller and various volute shapes. Figure 9 shows the streamline flow variation in the mixed-shape volute flow passage for various impeller shapes. The flow behavior in the volute flow passage was inconsistent with the changes in the impeller and volute shapes. Therefore, the hydraulic loss in the volute casing is inconsistent with various combinations of the impeller and volute casing.
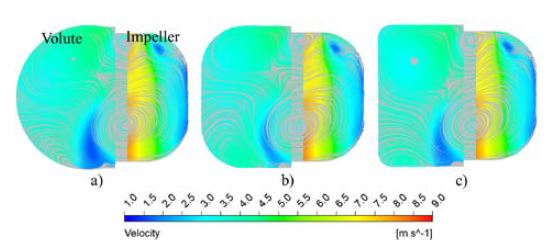
Velocity streamline with various volute shapes with mixed cross-section impeller a) MC, b) MM, and c) MR at BEP
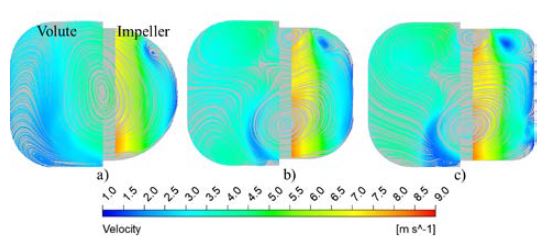
Velocity streamline with various volute shape with mixed cross-section impeller a) CM, b) MM, and c) RM at BEP
Among the cases, the circular cross-sectional shape of the impeller outlet with the three volute casing shapes exhibited a relatively lower loss value. These results match well with those of the pump hydraulic performance study, which shows a relatively higher pump efficiency from the combination cases with the circular cross-sectional shape of the impeller outlet. This indicates that the circular cross-sectional shape of the impeller outlet results in a lower flow passage loss and higher pump hydraulic efficiency.
Because sensitive materials such as fish and vegetables for transfer are vulnerable to injury or damage, the internal flow in the pump passage should be uniform and stable.
To quantitatively evaluate the effect of the combination of various cross-sectional shapes of the impeller outlet and volute casing on the swirl intensity, the swirl number was examined as shown in Figure 10. The swirl number evaluates the secondary flow and flow instabilities in the turbomachinery. The swirl number was calculated at various locations along the impeller passage. The swirl number is defined by Equation (5).
| (5) |
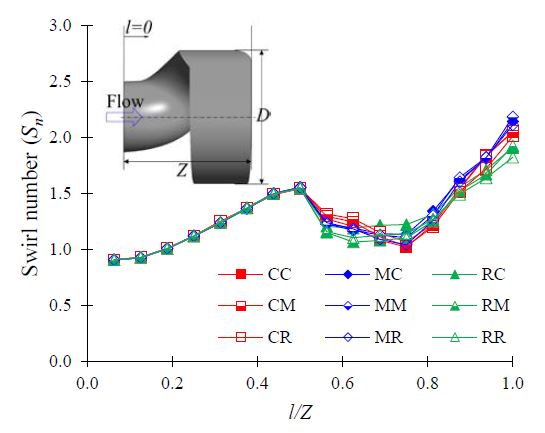
Swirl flow of single-channel pump models with the various impeller outlet and volute casing cross-sectional shapes at the design point
The values 0.0 to 1.0 l/Z indicate the axial locations from the impeller inlet to the impeller outlet. The results indicated that the internal flow of all models at the impeller inlet was similar, and the difference in the internal flow characteristics was mainly at the impeller outlet. However, the difference in the swirl intensity distribution of all the pump models was not significant.
4.3. Pump suction performance
Figure 11 shows the suction performance comparison between the single-channel pump models from the combination of three types of impeller outlet shapes and three types of volute casing shapes by CFD analysis. The cavitation number (σ) was calculated using Equation (6).
| (6) |
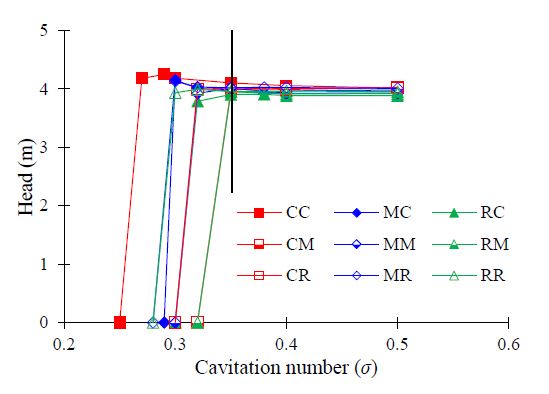
Suction performance of single-channel pump models with the various impeller outlet and volute casing cross-sectional shapes at design point
The result indicates that the suction performance of the circular cross-sectional shape of the impeller outlet with the circular cross-sectional shape of the volute casing model (Case CC) is better and distinguished from the other models. Moreover, in the case of matching different cross-sectional shapes of the impeller outlet and the same cross-sectional volute, the suction performance by the combination of the circular cross-sectional shape of the volute casing with different impeller outlet shapes showed relatively better suction performances than those of the other mixed and rectangular volute casing cross-sectional shapes.
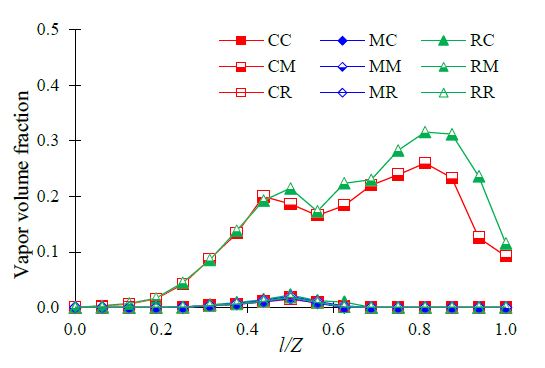
A cavitation number of 0.32 is selected for the comparison of the various cases. Figure 12 shows the averaged vapor volume fraction (VVF) distribution of the single-channel pump models with various impeller outlets and volute casing cross-sectional shapes at σ=0.32. The values 0 and 1 in the figure legend indicate liquid (water) and vapor (cavitation inception), respectively. The majority of the single-channel pump models had relatively small VVF values, and in the two model cases, CM and RM had relatively higher VVF values. The suction performance is highly dependent on the shapes of the impeller outlet and volute casing cross-section. Figure 11 shows that the critical cavitation number differs according to the case of the single-channel pump. The σ=0.32 is the critical cavitation number for cases CM and RM. The vapor volume fraction of 0.26 and 0.31 indicates the cavitation inception in the impeller of the CM and RM cases, respectively. This indicates that a well-matched pump combination may result in a relatively better suction performance. The measurement plane on l/Z = 0.7 planes was selected to evaluate the vapor volume fraction values at the cavitation number σ =0.32, as shown in Figure 13.
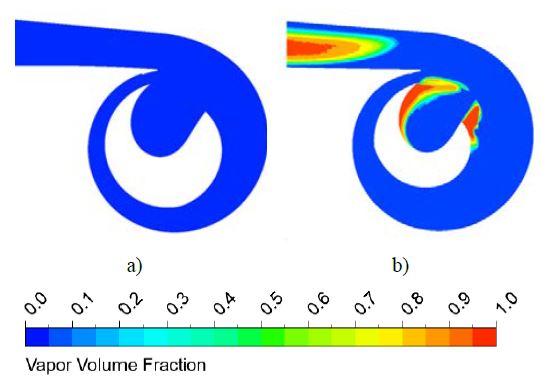
Vapor volume fraction contours of single-channel pump models with a) CC and b) RM on l/Z = 0.7 plane at σ=0.32
The single-channel pump with the cross-sectional shapes of a rectangular impeller outlet and mixed volute casing shows a higher VVF value than the other models on the measurement plane of l/Z = 0.7 at σ=0.32, which is strongly related to the suction performance in Figure 13. The relatively low suction performance may result in a higher possibility of cavitation inception in impeller and volute casing passages. In contrast, case CC, with the cross-sectional shapes of a circular impeller outlet and circular volute casing, showed a low VVF value on the measurement plane.
5. Conclusions
In this study, the matching performance of a single-channel pump with various cross-sectional shapes of the impeller outlet and volute casing combination was evaluated by CFD analysis. Circular, rectangular, and mixed cross-sectional shapes were used for the impeller outlet and volute casing cross-sections, respectively. According to the CFD analysis, the hydraulic and suction performances are highly influenced by the impeller outlet cross-sectional shape variation compared to the volute casing cross-sectional shape at the design point. Among the various models, the circular impeller outlet with the circular volute casing cross-sectional model had better hydraulic and suction performance than the other cases. The flow uniformity in the pump flow passage did not exhibit a considerable difference between the impeller outlet and volute casing matching combinations.
Author Contributions
Conceptualization, T. H. M. Hoang, U. Shrestha, and Y. D. Choi; Methodology, T. H. M. Hoang; Software, Y. D. Choi; Validation, T. H. M. Hoang, U. Shrestha, and Y. D. Choi; Formal Analysis, T. H. M. Hoang; Investigation, T. H. M. Hoang; Resources, Y. D. Choi; Data Curation, T. H. M. Hoang and U. Shrestha; Writing—Original T. H. M. Hoang; Writing—Review & Editing, Y. D. Choi; Supervision, Y. D. Choi; Funding Acquisition, Y. D. Choi.
References
- X. F. Guan, Modern Pump Theory and Design, Beijing, China Astronaut Publishing House, 2011 (in Chinese).
-
J. H. Kim, B. M. Cho, Y. S. Kim, Y. S. Choi, K. Y. Kim, J. H. Kim, and Y. Cho, “Optimization of a single-channel pump impeller for wastewater treatment,” International Journal of Fluid Machinery and Systems, vol. 9, no. 4, pp. 370-381, 2016.
[https://doi.org/10.5293/IJFMS.2016.9.4.370]

-
M. Guo and Y. D. Choi, “Effect of impeller blade thickness in the performance and internal flow characteristics of a single channel pump model,” The KSFM Journal of Fluid Machinery, vol. 23, no. 1, pp. 15-22, 2020.
[https://doi.org/10.5293/kfma.2020.23.1.015]

- X. Wu, H. Liu, and J. Ding, “Performance prediction of single-channel centrifugal pump with steady and unsteady calculation and working condition adaptability for turbulence model,” Transactions of the Chinese Society of Agricultural Engineering, vol. 220, Part E, pp. 85-91, 2006.
-
J. Keays and C. Meskell, “A study of the behaviour of a single-bladed waste-water pump,” Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, vol. 220, no. 2, pp. 79-87, 2006.
[https://doi.org/10.1243/09544089JPME60]

-
J. Pei, S. Yuan, and J. Yuan, “Fluid-structure coupling effects on periodically transient flow of a single-blade sewage centrifugal pump,” Journal of Mechanical Science and Technology, vol. 27, no. 7, pp. 2015-2023, 2013.
[https://doi.org/10.1007/s12206-013-0512-1]

-
O. Litfin, A. Delgado, K. Haddad, and H. Klein, “Numerical and experimental investigation of trailing edge modifications of centrifugal wastewater pump impellers,” Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Hawaii, USA, 2017.
[https://doi.org/10.1115/FEDSM2017-69123]

- A. J. Stepanoff, Centrifugal and Axial Flow Pumps: Theory, Design, and Application, 2nd edition, John Wiley & Sons, Inc, 1957.
-
R. C. Worster, “The flow in Volutes and Its Effect on Centrifugal Pump Performance,” Proceedings of the Institute of Mechanical Engineers, vol. 177, no. 31, pp. 843-875, 1963.
[https://doi.org/10.1243/PIME_PROC_1963_177_061_02]

- ANSYS Inc., ANSYS CFX Documentation, https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/prod_page.html?pn=CFX&pid=CFX&lang=en, , Accessed March 25th, 2019.
- ANSYS Inc., ANSYS ICEM Documentation, https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/prod_page.html?pn=ICEM%20CFD&pid=ICEMCFD&lang=en, , Accessed December 10th, 2018.
- F. R. Menter, M. Kuntz, and R. Langtry, “Ten years of industrial experience with the SST turbulence model,” Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, vol. 4, no. 1, pp. 625-632, 2003.