Study on verification of AFE rectifier control for electric propulsion ship
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Electric propulsion ships are frequently subject to fluctuations in the generator output voltage and current due to load variations from unpredictable environmental changes, including those of the maritime environment. The variation in the generator output affects the detection of the phase angle of the supply voltage, which is a key factor in the control of the active front end (AFE) rectifier of an electric propulsion system. In this study, an improved supply voltage phase-angle controller was proposed and applied to accurately detect the supply voltage phase angle required for the control of the AFE rectifier. The controller can be applied even under fluctuations in the output voltages of the generator owing to various circumstances that may arise in the electric propulsion ship. To demonstrate the effectiveness of the proposed improved supply voltage phase-angle controller, an irregular waveform with harmonics and zero-crossing in the output voltage of the generator was arbitrarily generated and inserted into the phase-angle detector. The proposed supply voltage phase-angle controller promoted a remarkable improvement in the phase-angle detection performance compared with that of the zero-crossing technique, a conventional method of phase-angle detection, even under irregular variations in the output voltage of the generator.
Keywords:
Electric propulsion, AFE rectifier, Zero-crossing technique, Phase-angle detector1. Introduction
In line with the strict environmental regulations of the International Maritime Organization (IMO), various types of technologies focused on environmental protection have been developed and applied. Among these technologies, the generation system of a four-stroke dual-fuel engine using gas generated by natural vaporization during the operation of a liquefied natural gas (LNG) carrier has been developed as a major propulsion method for electric propulsion ships.
In recent years, dual fuel technology using LNG as fuel has also been applied to large two-stroke engines, and the total number of orders for electric propulsion ships has decreased. However, when special types of propulsion performance are required, such as ice breakers and LNG carriers, an electric propulsion system is preferred.
In the case of large commercial vessels with electric propulsion systems, power is supplied through a four-stroke dual-fuel generator, and a power conversion unit is used to control the speed of the propulsion motor in an alternating current (AC) power system. The power conversion unit is composed of a rectifier, direct current (DC) link terminals, and an inverter. The performance improvement of the components constituting the power conversion unit is directly related to the efficiency of the electric propulsion system.
The rectification system of the electric propulsion system for vessels is largely categorized into diode front end (DFE) rectifiers employing diode elements and active front end (AFE) rectifiers using power semiconductors. In the case of DFE rectifiers, DC output waveforms are generated in the form of 6, 12, and 18 pulses, and at this time, the input power factor decreases owing to the harmonic distortion. To resolve this problem, a high-capacity passive filter and phase-shifting transformer are installed.
In the case of AFE rectifiers, it is possible to maintain a sine wave input current by using power semiconductors capable of high-speed switching. Thus, the installation of a passive filter or phase-shifting transformer is not required compared with the case of DFE rectifiers, which is advantageous in terms of cost and space required. AFE rectifiers have not been fully applied to large-scale electric propulsion ships owing to their capacity limitations. However, recent developments in power semiconductor technology have enabled the application of AFE rectifiers in large-sized electric propulsion ships[1].
As the AFE rectifier measures and controls the phase angle of the input voltage, accurate measurements are important. Although the zero-crossing technique has been commonly used for phase-angle measurement, the corresponding accuracy in the control of the rectifier is reduced when a voltage variation of the generator occurs owing to a sudden load change[2].
In this study, we propose an AFE rectifier with the application of an improved supply voltage phase-control technique that can accurately detect the phase angle of the rectifier even with sudden load variations. In addition, the phase angles were compared according to the conditions of the supply voltage variation, and the improvements provided by the phase-angle detector method for each condition were verified.
2. Electric Propulsion System Rectifiers
2.1 Overview of electric propulsion systems
The electric propulsion system obtains the output power necessary for the sailing of a ship by converting the high-speed low-torque energy of a prime mover into low-speed and high-torque energy to rotate the propeller. The system has been mainly used for special-purpose vessels, such as naval ships and cruise ships, from the early development stage to the present day. Since the 2000s, electric propulsion systems have been applied to large ships because of the improvement in performance and efficiency of the power conversion unit[3]. In recent years, with the development and optimization of control systems, their advantages have gained increasing attention. In addition, compared with traditional diesel engine ships, electric propulsion ships have several advantages, such as reduction of air pollutants, reduction of hull vibration and noise, and excellent maneuverability and braking ability.
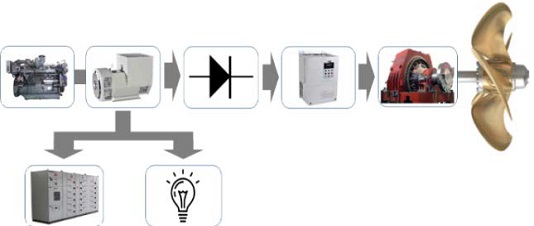
The electric propulsion system drives a generator with a prime mover, and the generated electric energy is supplied to a propulsion motor for ship propulsion. It is primarily composed of a prime mover, generator, power conversion unit, and propulsion motor, as shown in Figure 1[4]. The three-phase AC power generated by the generator is converted to DC in the rectifier of the power conversion unit and then converted into AC with a suitable frequency for the target RPM of the propulsion motor in the inverter and supplied to the propulsion motor. Synchronous or induction motors are used as propulsion motors.
The prime mover generally uses a four-stroke diesel engine, and a blushless synchronous generator is mainly used as the generator connected to the prime mover and shaft. The power conversion unit uses a power semiconductor switch for power conversion and flow control, and it is divided into AC-AC, AC-DC, DC-AC, and DC-DC conversion depending on the type of power converted. Compared with the conventional main engine of the mechanical propulsion type, the propulsion motor generates less vibration and noise and has high efficiency with excellent maneuverability and quick responses[5]. However, DC motors with complex structures and difficult maintenance have rarely been used, and induction and synchronous motors are mainly employed as propulsion motors.
2.2 DFE rectifier
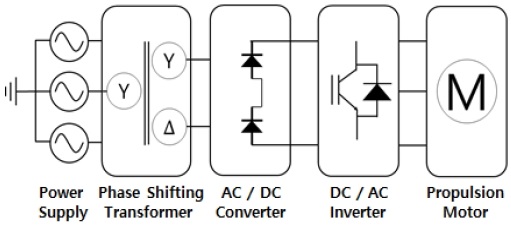
Figure 2 shows a block diagram of the electric propulsion system with a DFE rectifier. In this system, after converting the AC power generated by the three-phase AC generator to DC using a phase-shifting transformer and a diode rectifier, an inverter for frequency control capable of speed control is applied[6]. The diode rectifier has a simple circuit configuration, but it is directly connected to the power input terminal, which leads to an increase in the total harmonic distortion (THD) of the input current. The increase in THD generates harmonics, which adversely affect the entire power system of the ship and may cause failure of various electrical and electronic equipment.
To resolve this problem, a phase-shifting transformer is installed before the rectifier or passive filter is installed to increase the number of pulses to reduce harmonics, as shown in Figure 2 [7]. With the DFE rectifier method, the THD is large, in the range of 25–30 %, owing to harmonics of the 5th, 7th, 11th, and 13th orders or higher included in the input current. This does not satisfy the reference range of the IEEE Standard 519-2014 that specifies the values of THD as outlined in Table 1, which causes serious deterioration of the overall quality of the power system of the ship [8].
2.3 AFE rectifier
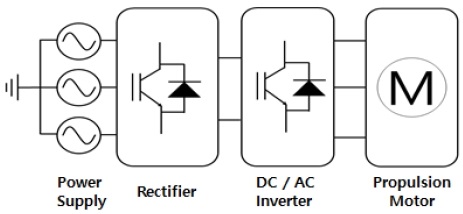
The AFE rectifier method converts the three-phase AC power produced by the generator into DC through active control, and uses IGBT, MOSFET, and GTO, which are power switches that can control the ON/OFF state, for the control of the rectifier. With this method, the input current on the power supply side can be maintained close to a sine wave, which has the advantage of improving the THD compared with the DFE topology. Figure 3 shows a block diagram of the electric propulsion system with an AFE rectifier. As this system does not require harmonic elimination, there is no need to install a phase-shifting transformer, as required in the DFE topology. This leads to advantages such as improvement of the overall system power efficiency and simplification of the installation space in the engine room. However, the AFE topology has disadvantages in terms of power loss during the ON/OFF control of the power switch and the fact that it is more costly and requires maintenance compared with the DFE rectifier method[9].
3. Mathematical Modeling of AFE Rectifier
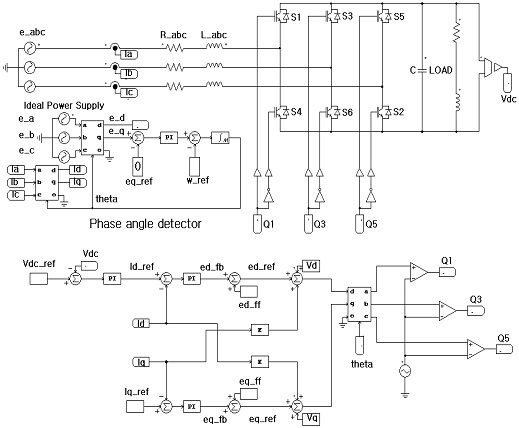
Figure 4 shows the basic circuit diagram of the AFE three-phase rectifier. The AFE rectifier consists of three terminals and six switches, and the AC powers ea, eb,and ec maintain the three-phase equilibrium. In addition, inductors L1, L2, and L3 installed on the power output side are used to control the magnitude of AC currents ia, ib, and ic at power conversion, and the capacitor “C”on the output side of the rectifier is installed for stable DC voltage output of the DC-link terminal even under rapid variations in the voltage[10].
The equations for the sum of the phase voltage and phase current of the three-phase AC power are expressed as follows:
| (1) |
| (2) |
where ea, eb, and ec denote the supply voltages of the a, b, and c phases, respectively, and ia, ib, and ic denote the respective phase currents.
The voltage equations of the AFE rectifier in each phase are as follows:
| (3) |
| (4) |
| (5) |
where Va, Vb, and Vc are the input voltages of the rectifier.
As the voltage equation of the AFE rectifier is expressed as three-phase AC values with a continuous change in the values of voltage and current over time, the rectifier control becomes complicated. If the three-phase AC power can be expressed by coordinate transformation with respect to an arbitrary reference axis, the voltage equation can be converted into an equation with a constant DC value, thereby simplifying the control of the rectifier and improving the accuracy of the control. In the improved supply voltage phase-angle controller proposed in this study, the three-phase axes a, b, and c are converted into the stationary α − β axis, and the coordinate transformation is performed on the d − q axis of the synchronous rotating coordinates.
In the axis transformation process to the stationary α − β axis shown in Figure 5, the phase variable fa for an arbitrary time can be represented as the sum of fa cos θ, the α-axis component, fb sin θ, and the β-axis component. Then, if phases b and c are expressed as a matrix as with the a phase, the three-phase variable is transformed into a stationary α − β component. When we set θ = 0° to match axes α and β, neglecting the zero sequence, we obtain Equation (6) as follows:
| (6) |
After the transformation of the three-phase axes a, b, and c to the stationary α − β axis using Equation (6), the voltage equations are presented as shown in Equations (7) and (8) as follows:
| (7) |
| (8) |
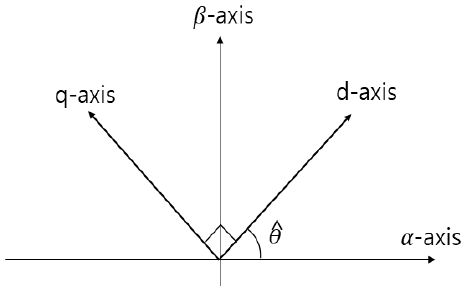
In addition, the transformation of the stationary α − β axis component to the d − qaxes on the synchronous rotating coordinates can be represented as shown in Figure 6, and the values can be represented as the values of the synchronous rotating coordinates.
Equations (9) and (10) are voltage equations converted from those of the stationary α − β axis to the synchronous rotating d − q axis. Through the coordinate transformation process, the three-phase AC values that continuously change over time can be converted into two easy-to-control DC values, and the d − q axis value obtained by transformation to synchronous rotating coordinates is used to control the AFE rectifier.
| (9) |
| (10) |
4. Comparison of the Different Phase-Angle Detector Methods for the AFE Rectifier
4.1 Conventional phase-angle detector method for the AFE rectifier
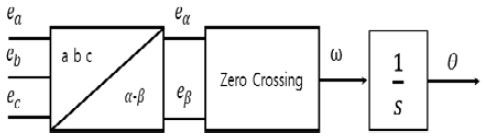
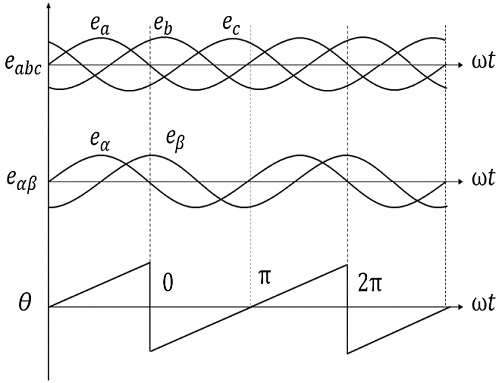
In the conventional method with AFE rectifiers, a zero-crossing technique is used to derive the phase angle for the control. As shown in Figure 7, the zero-crossing technique measures the power supply voltage and finds the zeroes that occur at each half cycle to detect the current phase-angle θ.
To obtain the phase angle, as shown in Figure 8, the point at which the supply voltage of a phase changes from positive to negative is set as the reference angle 0° to obtain the phase angle θ for the control. In addition, through the coordinate transformation from the three-phase voltages ea, eb, and ec to the stationary α − β axis to obtain ea and eb, the required phase-angle θ can be directly obtained.
The zero-crossing technique enables simple acquisition of the phase angle for controlling the rectifier; however, as the voltage and current outputs from the generator are subjected to frequent variations due to sudden changes in the load from various environmental factors, such as water depth, draft, speed, and wind on the ship, there are cases in which the output waveform of the supply voltage has an irregular shape. When this irregular shape is supplied to the input of the phase-angle detector, an error occurs in the detected phase angle, which affects the control of the rectifier.
4.2 Proposed phase-angle detector method of the AFE rectifier
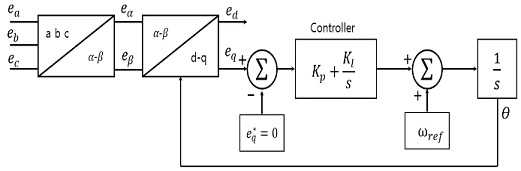
In AFE rectifiers, for coordinate transformation into the d − q axis and to obtain the current reference value that is in phase with the phase of the supply voltage, accurate detection of the phase-angle θ is essential. Figure 9 shows a block diagram indicating the configuration of the supply voltage phase-angle controller to obtain the phase-angle θ. The controller performs coordinate transformation of the three-phase AC supply voltage to the stationary α − β axis and then to the synchronous rotating coordinate d − q axis to obtain ed and eq, the voltages with easy-to-control DC values; ed and eq are arbitrarily set to be the active and reactive power components, respectively, and the control is performed such that the value of the reactive power component eq becomes 0.
Ps in Equation (11) represents the active power supplied by the power supply unit.
| (11) |
In Equation (11), as the eq voltage is controlled to be 0, the power is only affected by ed, which represents the d-axis voltage. In addition, as the q-axis voltage has no effect on the power, the supply power becomes .
Therefore, when all active power components are set to be on the d axis and the voltage on the q axis is controlled to be 0, the actual phase-angle θ becomes equal to the imaginary phase-angle θ^, thereby obtaining an accurate phase-angle θ. If the phase angle is detected by constructing the supply voltage phase-angle controller based on this principle, the synchronous rotating q-axis voltage of the controller can always be controlled to be 0, even in an irregular supply voltage waveform with harmonics or noise, and an accurate supply voltage phase-angle θ can be obtained.
5. Simulation for Verification of the Proposed AFE rectifier
To demonstrate the effectiveness of the improved supply voltage phase-angle detector proposed in this study, a waveform with instantaneous zero-point noise and harmonics was supplied to the supply voltage output from the generator, and the change in the phase-angle θ derived from the phase-angle detector and the resulting waveform output of the DC link voltage were analyzed using simulation. The values of the system parameters used in the simulation are listed in Table 2.
5.1 Simulation of the conventional phase-angle detector method of the AFE rectifier
Figure 10 shows a diagram of the AFE rectifier with the application of the zero-crossing phase-angle detector method, which is the conventional phase-angle detection method. In this method, the current phase-angle θ is detected by measuring the supply voltage and finding the zeroes that occur every half cycle.
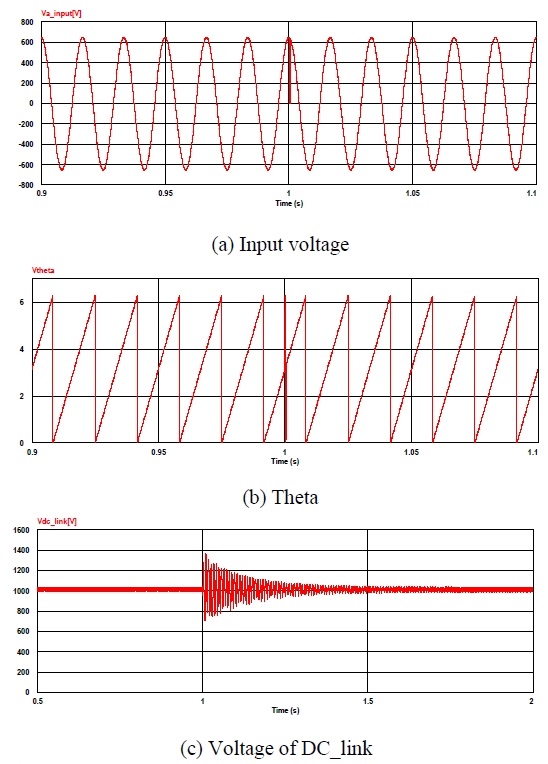
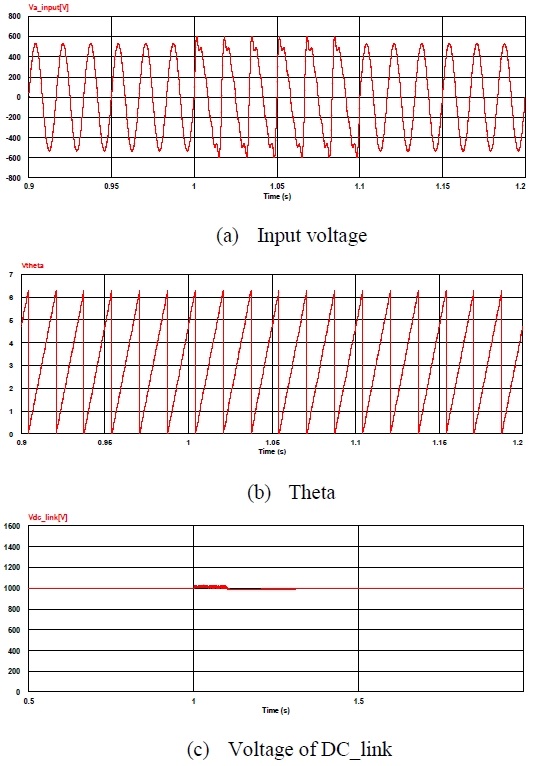
Figure 11 shows the simulation results showing the detected phase angle and DC link voltage after the zero noise was inserted into the supply voltage at a time of 1 s. The results showed that the phase angle obtained by the zero-crossing technique was momentarily distorted in the 1-s section where the zero-point noise was generated, and the DC link voltage showed a variation in this section.
Figure 12 shows the simulation results showing the detected phase angle and DC link voltage after harmonics were inserted into the supply voltage at 1 to 1.1 s. The results indicate that the phase angle obtained by the zero-crossing technique was severely distorted in the section where the harmonics were generated, and the DC link voltage showed the voltage-hunting phenomenon in this section.
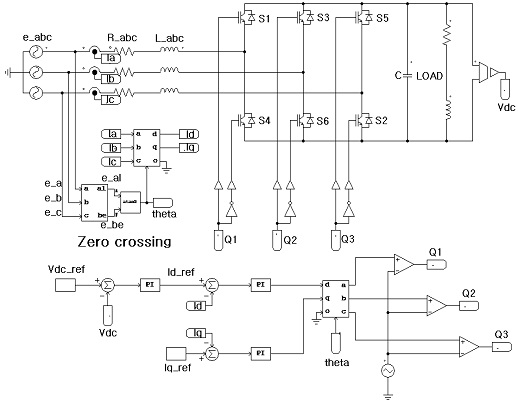
5.2 Simulation of the improved phase-angle detector method of the AFE rectifier
Figure 13 shows a schematic diagram of the AFE rectifier control system with the application of the improved phase-angle detector proposed in this study. To verify the effectiveness of the proposed method over the conventional method using the measured supply voltage, a supply voltage waveform with zero-point noise, phase change, and harmonics was supplied to the input side of the phase-angle detector. The results were analyzed using a simulation.
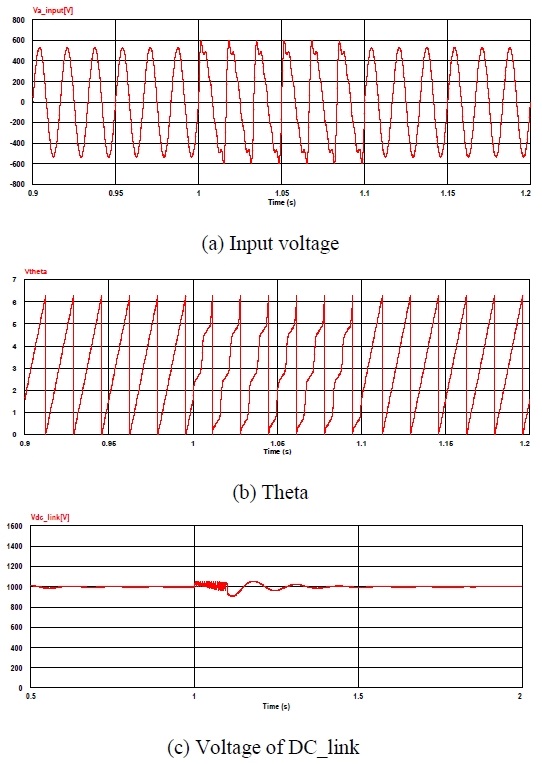
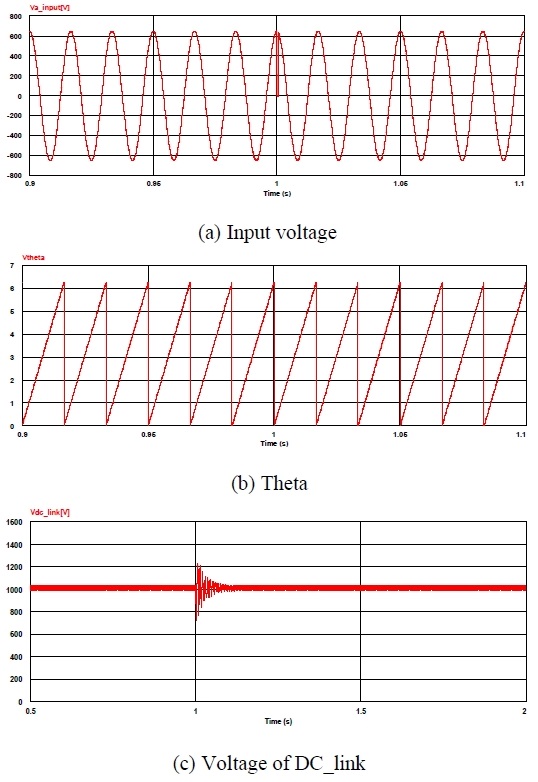
Figure 14 shows the simulation results showing the detected phase angle and DC link voltage after zero noise was inserted into the supply voltage at 1 s. The results indicate that an accurate phase angle could be obtained without change even in the 1-s section, where the zero-point noise was generated using the proposed phase-angle detector method in this section. The output of the DC link voltage also improved compared with that of the conventional method.
Figure 15 shows the simulation results, showing the detected phase angle and DC-link voltage after harmonics were inserted into the supply voltage at 1 to 1.1 s. The results indicate that an accurate phase angle could be obtained, even in the section where the harmonics were generated, with the application of the proposed phase-angle detector method, in which a stable output of the DC link voltage was obtained compared with that of the conventional method.
6. Conclusions
In this study, considering the voltage output characteristics of an AFE rectifier for electric propulsion systems, the voltage output obtained by applying the improved phase-angle detector method was compared to the output obtained by applying the conventional zero-crossing method.
In the conventional method, the AFE rectifier detects the phase angle from the generator supply voltage and uses the phase angle to control the rectifier. However, for the generator output voltage of a ship, there are cases of instantaneous irregular waveform output due to various causes, such as load variations and switching of the power conversion unit, which leads to errors in the phase-angle measurement and instability in the control of the rectifier.
The improved supply-voltage phase-angle controller method proposed in this study performs the coordinate transformation from the stationary α − β axis to the d − q axis of the synchronous rotating coordinates to obtain voltages ed and eq, and ed is set as the active power component, whereas eq is arbitrarily set to be the reactive power component. Accurate measurement of the phase angle is possible with the proposed method by controlling the value of eq and maintaining the reactive power component at 0. To prove the effectiveness of the proposed phase-angle detector, a simulation of supplying an irregular waveform with zero noise and harmonics injected to the AC power of the generator supplied to the detector was simulated. As a result of the simulation, when zero noise occurred, the peak-to-peak value of the noise generated in the DC output voltage of the DC link terminal was reduced by 200 V compared with the conventional phase-angle detection method, and even when harmonics are included, the DC output voltage is more stable than that of the existing method with the desired result.
Acknowledgments
This work was supported by the Korea Maritime & Ocean University Research Fund.
Author Contributions
This research presented in this paper was wholly contributed by the Corresponding Author.
References
- H. M. Jeon, A Study on the Performance Improvement for AFE Rectifier, M. S. Thesis, Department of Marine System Engineering, Korea Maritime & Ocean University (KMOU), 2018 (in Korean).
-
W. F. Egan, Phase-Lock Basics. Wiley-IEEE, 2007.
[https://doi.org/10.1002/9780470178737]

- T. J. McCoy, “Trends in ship electric propulsion,” IEEE Power Engineering Society Summer Meeting, vol. 1, pp. 343-346, 2002.
- W. Bin, High-Power Converters and AC Drives, Wiely-IEEE, 2017.
- A. E. Fitzgerald, Electric Machinery. Mc Graw Hill, 2002.
- C. A. M. Vasquez, A Methodology to Select the Electric Propulsion System for Platform Supply Vessels, M. S. Thesis. Sao Paulo: Naval Architecture and Ocean Engineering, CollegeEscola Politécnica, 2014.
- P. N. Kapil & Cheta and M. Dhrangadharia, “Design and simulation of three-phase voltage source based converter for HVDC applications,” International Journal of Electronic and Electrical Engineering, vol. 7, no. 6, pp. 573-579, 2014.
-
A. J. Watson, P. W. Wheeler, and J. C. Clare, “A complete harmonic elimination approach to DC link voltage balancing for a cascaded multilevel rectifier,” IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, vol. 54, no. 6, pp. 2946-2953, 2007.
[https://doi.org/10.1109/TIE.2007.906993]

-
Y. W. Li, M. Pande. N. R. Zargari, B. Wu, “An input power factor control strategy for high-power current-source induction motor drive with active front-end,” IEEE TRANSACTIONS POWER ELECTRON, vol. 25, no. 2, pp. 352-359, 2010.
[https://doi.org/10.1109/TPEL.2009.2028344]

-
S. Kim, B. Cho, S. Sul, Consideration of active-front-end rectifier for electric propulsion navy ship, 2013 IEEE Energy Conversion Congress and Exposition, pp. 13-19, 2013.
[https://doi.org/10.1109/ECCE.2013.6646675]