The Korean Society of Marine Engineering

[ Original Paper ]

Journal of Advanced Marine Engineering and Technology - Vol. 45, No. 6, pp.392-397

ISSN: 2234-7925 (Print) 2765-4796 (Online)

Print publication date 31 Dec 2021

Received 28 Sep 2021 Revised 02 Nov 2021 Accepted 23 Nov 2021

DOI: https://doi.org/10.5916/jamet.2021.45.6.392

Study on the simulation of the dynamic characteristics of a marine diesel generator

Kim, Hee-Moon¹

; Hyeonmin Jeon²

; Kyoungkuk Yoon³

; Kim, Jong-Su^†

1Senior Researcher, Korea Marine Equipment Research Institution, Tel: +82-51-400-5077 hmkim@komeri.re.kr
2Professor, Division of Marine System Engineering, Korea Maritime & Ocean University, Tel: +82-51-410-4841 jhm861104@kmou.ac.kr
3Professor, Division of Marine System Engineering, Korea Maritime & Ocean University, Tel: +82-51-410-4265 kkyoon@kmou.ac.kr

Correspondence to: ^†Professor, Division of Marine System Engineering, Korea Maritime & Ocean University, 727, Taejong-ro, Yeongdo-gu, Busan 49112, Korea, E-mail: jongskim@kmou.ac.kr, Tel: +82-51-410-4831

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In order to implement the recent carbon-neutral policy and the International Maritime Organization (IMO)'s CO2 reduction strategy, active research on the application of various eco-friendly technologies to existing ship systems is underway. As engine-based synchronous generators, which are the traditional power generation sources for ships, inevitably produce exhaust emissions during the combustion process, there is an urgent need to develop technologies for alternative power generation sources. However, it is difficult to completely replace engine generators with fuel cells, ESSs, and renewable energies that are currently being considered owing to several factors such as economic feasibility and energy density per volume. Therefore, a hybrid power generation system that integrates various generation sources into the power system without producing exhaust emissions is expected to be a short-term alternative to engine generators. It is important to simulate and verify the overall system prior to loading ships using this new system, as the dynamic characteristics of the existing engine generator, which serves as the main power source within the hybrid power generation system, affect the entire system. In this study, the main parameters of the engine, governor, exciter, and synchronous machine were identified to simulate the dynamic characteristics of the engine generator for ships. Moreover, the gain of the governor transfer function was selected using the Routh–Hurwitz criterion to obtain a response similar to that of an actual engine. Finally, dynamic characteristics resembling those in a real-life situation were confirmed for the engine, governor, exciter, voltage, and current by simulating the entire power system with varying power loads.

Keywords:

Marine diesel engine, Hybrid power system, System simulation, Governor, Routh-Hurwitz criterion

1. Introduction

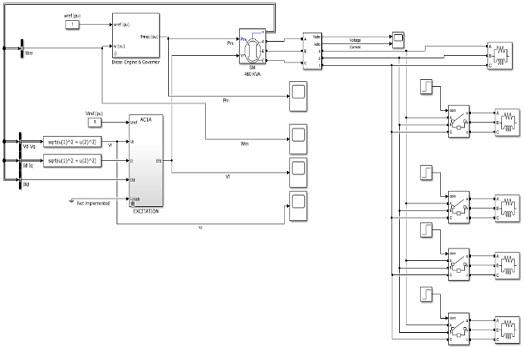
As a hybrid generation system that integrates various power sources into the power system of ships has been actively investigated, there is an increasing need to verify its performance and stability through simulations before field testing. A hybrid power generation system is configured with a traditional diesel-engine-based synchronous generator as the main power source, and other generation sources, such as energy storage systems (ESSs) and fuel cells, are connected to the system. To confirm the dynamic characteristics of the overall system, it is important to model individual generation sources and, in particular, the engine generator used as the main power source.

Traditional generators for ships are mechanically connected to the rotating shaft of a four-stroke engine to generate electrical energy using the rotational torque from the engine [1]. During this process, a synchronous machine is typically used for the generator connected to the rotational shaft of the engine. This machine has control devices, such as a governor and an exciter, to ensure a stable power supply. The governor determines the output of the engine by adjusting the amount of fuel injected into the cylinder, and the exciter controls the output voltage by supplying the current to the field winding of the generator.

In this study, individual parameters were identified for the simulation model of a marine synchronous generator consisting of a governor, an exciter, and other devices, and the adequacy of the parameters for the governor was determined using the Routh–Hurwitz criterion. Finally, the response characteristics of the diesel generator were examined under various load scenarios.

2. Marine Synchronous Generator

2.1 Configuration of the Marine Synchronous Generator

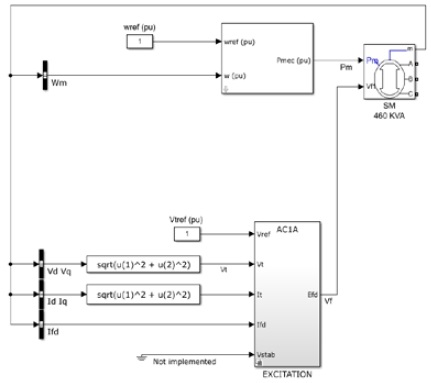
As shown in Figure 1, a marine synchronous generator consists of an engine and a governor, which generate torque, an exciter, which maintains a constant output voltage, and a synchronous machine. The governor generates the torque required by the generator by adjusting the amount of fuel injected into the engine cylinder and ultimately ensures that the generator engine maintains a constant rpm.

Figure 1:

Synchronous generator modeling for a ship

As shown in Equation (1), the rotational speed of the generator determines the power frequency, while the engine governor controls the power frequency. In the equation, rpm represents the revolutions per minute of the generator, f is the frequency, and P is the number of poles.[2]

r p m = 120 f p

(1)

The exciter generates a magnetic flux at each pole and maintains a constant voltage by controlling the amount of current that is conveyed to the field winding of the rotor.

E = 4.44 f N ∅ K w

(2)

Equation (2) expresses the induced electromotive force of the synchronous generator, where E is the voltage, N is the number of windings, Φ is the magnetic flux, and K_w is the winding factor.[2] If the number of the windings is excluded, and the winding factor is considered a constants in the equation, the voltage is determined by the magnitude of the frequency and magnetic flux. As mentioned above, because the frequency is controlled by the engine and the governor, the voltage is maintained through the flux control of the exciter under the assumption of constant frequency.

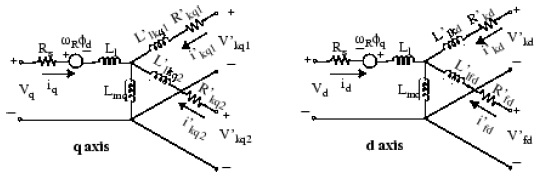
While the synchronous machine consists of three phases, it is generally represented in the d and q axes using the Clarke and Park transformations for convenience of control [3].

Figure 2:

Equivalent circuit of the synchronous machine (d-q)

2.2 Governor and Engine Model

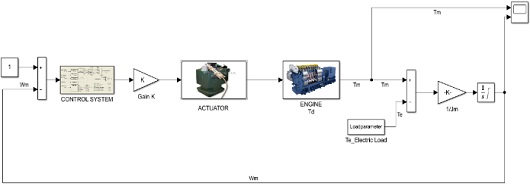
The model for engine control can be represented in terms of the governor controller, actuator according to the fuel injection mechanism, and time delay of the engine. When the engine speed changes with varying power load on the board, an error signal based on the set values controls the amount of fuel injection through the governor controller and actuator. A time delay occurs before the mechanical torque is generated through fuel injection and strokes inside the cylinder. Figure 3 shows the model for such an engine [4][5].

Figure 3:

Components of the model for the governor and engine system

Ultimately, the rotational speed of the engine and generator is controlled such that the set values are maintained at all times, thereby maintaining the power frequency.

2.3 Exciter Model

For the synchronous generator to produce power with a constant voltage and frequency, a magnetic flux that is linked to the torque of the rotor is required. The magnetic flux is controlled by the exciter.

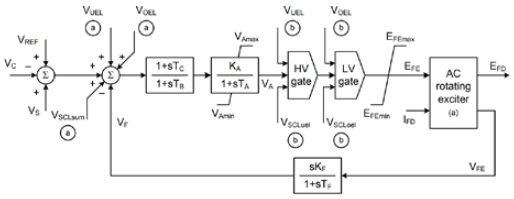
A self-excitation brushless exciter system is used in marine generators [6], and a permanent magnet generator is also applied to the exciter system in emergency generators. As shown in Figure 4, the AC1A-type exciter system proposed by the IEEE [7] was applied in this study. The preset reference voltage Vref (pu) was compared to the output voltage and was used as a field voltage command.

Figure 4:

Block diagram of an AC1A-type exciter system

Typical data from MATLAB Simulink were used for the parameters of the exciter, and the corresponding values are listed in Table 1.

Table 1:

Parameters for excitor modeling

2.4 Synchronous Machine Model

A salient-pole synchronous machine was selected to model the synchronous generator. The typical data of a 460 V, 1,800 rpm synchronous machine were used in MATLAB Simulink; the corresponding values are listed in Table 2.

Table 2:

Parameters of the synchronous machine

3. Selection of the Governor Gain

3.1 Transfer Functions of the Governor Controller and Actuator

As mentioned above, when modeling the governor, the system response is determined by the responses of the controller and actuator, as well as by the time delay occurring during the engine combustion process.

H c s = T 3 s + 1 T 1 T 2 s 2 + T 1 s + 1

(3)

The transfer function of the governor controller, Hc(s), can be represented as shown in Equation (3), where T₁, T₂, and T₃ refer to the time constants for the controller.

H a s = T 4 s + 1 s T 5 s + 1 T 6 s + 1

(4)

The transfer function of the governor actuator, Ha(s), can be represented as shown in Equation (4), where T₄, T₅, and T₆ refer to the time constants for the actuator.

3.2 Determination of Gain (K) for a Stable Response

The transfer function of the governor and controller H(s) is given by Equation (5).

H s = T 3 s + 1 T 4 s + 1 s T 1 T 2 s 2 + T 1 s + 1 T 5 s + 1 T 6 s + 1

(5)

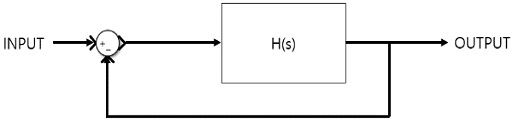
The transfer function of the governor and engine system can be simplified as a feedback system G(s), as shown in Figure 5 and Equation (6).

G s = K H s H s + 1

(6)

Figure 5:

Simplification of the transfer function of the governor and engine system

Table 3 lists the time constants for the governor and engine selected in this study.

Table 3:

Parameters of the governor and engine model

3.3 Selection of the Gain Using the Routh–Hurwitz Criterion

Generally, a system is said to be stable when the output is finite for a finite input. Additionally, the natural response of such a system decreases to zero when the time becomes infinite. Thus, the system is stable when the poles of the system are negative real numbers on the left-hand side or the s-plane. While the exact location of the poles is not known, the Routh–Hurwitz criterion is widely used to evaluate the stability of the system by identifying whether the poles are located on the left or right plane [8]. In this study, the optimal gain values for the time constants in Table 3 were determined using the Routh–Hurwitz criterion.

Table 4 lists the Routh table for the poles obtained by expanding the transfer function, G(s), while excluding the K gain value of the system. As no change in sign of the values in the first column was observed, the system can be considered stable.

Table 4:

Routh table for the pole of G(s)

Using the corresponding transfer function and the table above, the optimal gain value (K) for a stable system response was calculated as greater than 0 and less than 40.50976. The optimal K value was found to be 15 by simulating the speed and torque estimates of the governor and engine based on the electrical load input.

Figure 6:

Simulation for regulator gain tuning

4. Simulation

4.1 Load Scenarios to Verify Modeling of the Dynamic Characteristics of the Generator

The power loads listed in Table 5 were applied to verify the modeled dynamic characteristics of the marine diesel generator. After applying an initial load of approximately 50%, the load was increased every three seconds to examine the changes in the generator and power system. In addition, a scenario in which the generator output was exceeded by the final power load was simulated to determine whether the model would generate results similar to those obtained in real-life situations.

Figure 7:

Engine generator modeling for a dynamic load

Table 5:

Simulation scenario for the electric load connection

4.2 Simulation of the Dynamic Characteristics of the Generator with a Varying Load

The transient response of the system was examined by applying the power loads listed in Table 5 for 13.

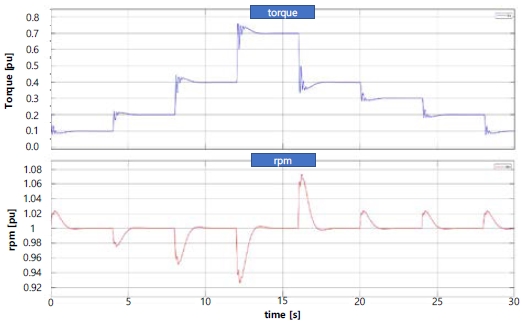
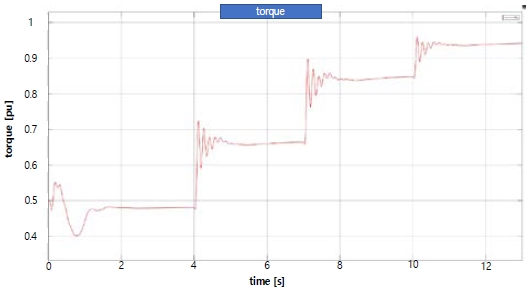
Figure 8 shows the results of simulating the rotational speed of the generator. An identical load of 200 kW was applied after 4–7 s, and a load of approximately 100 kW was applied after 10 s. The results demonstrate that the rotational speed of the engine quickly recovered to the set value.

Figure 8:

Rotation speed of the generator [pu]

Figure 9 shows the simulation results for the rotational torque of the engine. The required rotational torque increased as the power load increased, and the controller and engine responded quickly to the required value.

Figure 9:

Mechanical input of the synchronous machine [pu]

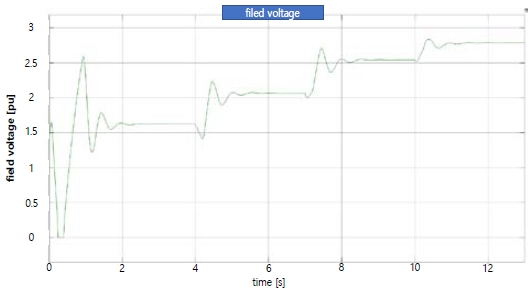
As shown in Figure 10, the magnitude of the required field voltage increased as the power load increased, and the exciter and exciter systems responded quickly to the required value.

Figure 10:

Filed voltage for the synchronous machine [pu]

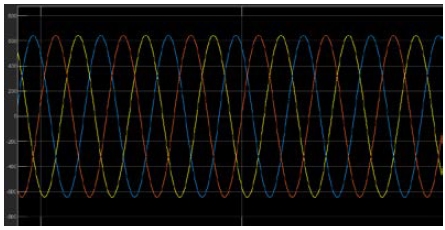
Figure 11 shows the simulation result for the three-phase line-to-line voltage. It can be seen that the sine waves do not exhibit distortions.

Figure 11:

Three phase line-to-line voltage [V]

4.3 Applying a Power Load Above the Upper Limit of the Engine Output

In the actual marine generator load test, the upper limit of the engine output was set to 110%, and the mechanical device of the governor was adjusted accordingly. Based on the load scenario in Table 5, the total load was set to 1,250 kW to simulate the range outside the output of the generator at 14 s.

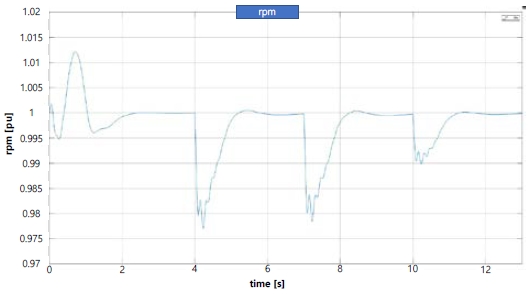
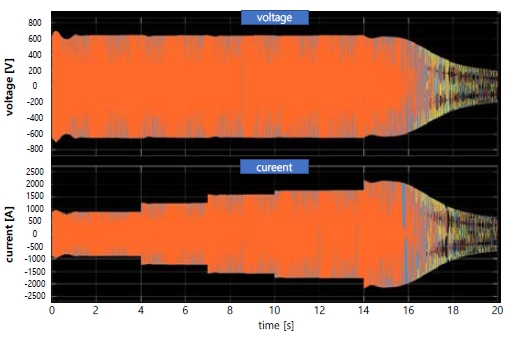
The results in Figure 12 show that the rotational speed of the engine generator decreased after 14 s. Beyond 14 s, the electric load is greater than the engine output, as the applied power load is at least 110% of the engine output. As the rotational speed of the engine decreases, the frequency and terminal voltage of the generator also decrease, which in turn increases the field voltage of the generator.

Figure 12:

Simulation result for Pm, Wm, Vf for the over load [pu]

As shown in Figure 13, the magnitudes of the system voltage, current, and frequency continued to decrease after 14 s. In an actual ship, a power management system detects a decrease in frequency, and an air circuit breaker isolates the generator from the system. In this case, if the system is not connected to an idle generator, the ship may encounter a blackout state. Stable maintenance of the voltage and an increasing current with load application can be observed up to 14 s.

Figure 13

Simulation results for the voltage and current for the over load [V, A]

5. Conclusions

In this study, a model with output, system voltage, and current responses similar to those of the generator and power system of an actual ship was established. The parameters of the governor, engine, exciter, and synchronous machine necessary to simulate the dynamic characteristics of a marine engine generator were first identified. The governor gain was then selected using the Routh–Hurwitz criterion, which is widely used to verify system stability. Additionally, after simulating the overall system in island mode operation of the marine generator, a power load was applied to confirm the dynamic characteristics of the generator. Subsequently, the model was used to simulate the parallel operation of marine generators and the entire PMS. Additional research on the hybrid generation system will be conducted as a future task by applying the fuel cell, ESS, and renewable energy models to the system.

Author Contributions

Writing-Original Draft Preparation, H. M. Kim; Writing-Review & Editing, H. M. Kim and H. M. Jeon; Supervision, J. S. Kim and K. K. Yoon; Project Administration, J. S. Kim and K. K. Yoon.

References

H. C. Cho, “Robust adaptive voltage control of electric generators for ship,” The Journal of Institute of Control, Robotics and Systems, vol. 22, no. 5, pp. 326-331, 2016 (in Korean). [https://doi.org/10.5302/J.ICROS.2016.16.0027]
S. H. Kim, J. S. Kim, S. J. Oh, and H. S. Kim, Practical Electrical Machinery, Seoul, Korea: Seonandang, 2011 (in Korean).
P. Krause, et al., Analysis of Electrical Machinery and Drive Systems, 3rd Edition, New Jersey, USA: Wiley-IEEE Press, 2002. [https://doi.org/10.1109/9780470544167]
S. Benhamed, H. Ibrahim, K. Belmkhtar, H. Hosni, A. Ilinca, D. Rousse, A. Chandra, and D. Ramdenee, “Dynamic modeling of diesel generator based on electrical and mechanical aspects,” IEEE Electrical Power & Energy Conference, pp. 1-6, 2016. [https://doi.org/10.1109/EPEC.2016.7771756]
Jeon. H. J and J. S. Choi, Internal Combustion Engine Lecture, Seoul, Korea: Hyosung Publishing, 2004 (in Korean).
Y. C. Kim, A Study about the Governor Characteristic Test of the Emergency Diesel Generator on a Clear Power Plant, M. S. Thesis, Chungnam National University, Korea, 2019.
IEEE Standards Board, “IEEE recommended practice for excitation system models for power system stability studies,” 1992.
N. S. Nise, Control Systems Engineering, 7th Edition, USA, pp. 283-299: Wiley, 2010.