Numerical investigation of a tidal stream turbine using two methods of the Multiple Reference Frame and the Actuator Disk Momentum
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Numerical investigation of the flow around an axial tidal turbine were investigated. Two different methods to model the flow around the tidal turbine, the multiple reference frame method and the actuator disk momentum method, were used and compared in terms of accuracy and computational efficiency. Discretization errors were performed for Power and Thrust coefficients. Numerical prediction compared favourably to the experimental measurements from physical tests of the tidal turbine in homogenous flow. The Multiple Reference Frame method was used to compute power coefficient and thrust of a tidal turbine at different tip speed ratios, the forces that act on the turbine blades, and the pressure distributions at each blade cross sections. we performed all our simulations at the best efficient point. We found that the maximum stresses on the turbine blade occurred at turbines radius between 0.8 and 0.9Ro, where Ro is the turbine bald radius. The optimum radial and longitudinal distances were studied for installing other turbines to produce optimum power output. We conclude that a farm of our presented turbines, which gives the maximum output power for each turbine, can be arranged with the turbines being separated by three times the turbine’s radius.
Keywords:
Stream tidal turbine, Turbine blade forces, RANS equations, Multiple Reference Frame, Actual Disk Method, Physical tests and validation1. Introduction
Tidal energy from oceans and seas can be a useful form of power. Tidal turbines use the kinetic energy of tides to produce electrical energy directly. There are three main types of tidal turbines: dynamic, barrages and tidal stream turbines [1]. Tidal stream turbines are submerged in the sea, and are installed without making visual obstructions above the sea surface. However, the underwater installation of the Tidal turbine is considered a difficult task. Most of the studies on the wakes of tidal stream turbines used either semi analytical methods or, due to the complexity of the turbine and the excessive computer time required for an analysis, the actuator disk momentum (ADM) method based on Reynolds-averaged Navier Stokes equations (RANSE). The ADM method represents the turbine rotor as a disc characterized by various coefficients [2][3].
turbine wake interactions of a tidal turbine farm at different flow speeds ranging from 0.4 to 1 m/s and different inlet turbulence intensities (I) ranging from 3% to 15 %. Nguyen et al. [5] used the ADM method to test several different turbulence models, such as the Standard and the Realizable k-ϵ, the k-ω (SST) and the Reynolds Stress (RSM) turbulence models [6]. They compared their results to experimental results and added a source term to the turbulence equation. They found that the RSM turbulence model gave the best agreement with the experimental results, and found that the Standard k-ϵ gave the best agreement. Abolghasemi et al. [7] implemented the ADM method with adaptive mesh, took into account the turbulence characteristics. They compared the results with analytical results. Their optimized mesh succeeded in getting good results for the wake behind a tidal turbine with relatively low cost of computations, and showed that the k-ω (SST) turbulence model was able to give an accurate result for far wake turbulence.
However, close to turbine’s wakes corrections of the turbulence model had to be modeled. Gebreslassie et al. [8] studied the accuracy of the ADM method to assess the wake characteristics of a tidal turbine. Blackmore et al. [9] performed CFD simulations of the flow around a tidal turbine using large eddy simulation (LES) turbulence model [6] for different turbulence intensity (I). They showed that, by increasing the I and the integral length scale, the location of the maximum velocity deficit got close to the disk which represented the turbine. Blackmore et al. [9] found that the turbulence intensity has a small effect on wake width, and that the integral length scale has a noticeable effect on the turbulence width. Jeromin et al. [10] modified the ADM method and compared results to the blade element method (BEM) [11] as well as to the ADM method implemented in the commercial CFD software ANSYS Fluent [12]. Koh and Ng [13] studied the effect of different blockage ratios (the ratio between the turbine swept area and the water channel area) of a single tidal turbine using the ADM method with constant water channel depth. They found that the thrust increases the blockage ratio increases. Further on, they found that the decay rate of I is affected by the water canal depth. Nishino and Willden [14] used the ADM method to study various blockage and aspect ratios of a tidal turbine. They used the RANSE solver to compute a turbine in a rectangular water canal. They introduced a new approach to take into consideration the effect of turbulence produced by the turbine blades.
Hunter et al. [15] used the ADM method to model a tidal turbine. They studied the effect of varying the operating conditions across an array of turbines. They found that the maximum power is achieved when thrust coefficients on the array of turbines are the same. They also found that the maximum average power coefficients in the front and rear rows of turbine are decreased by increasing the streamwise spacing and are less than the values of non-staggered turbine. Nishino and Willden [16] studied two tidal turbines to evaluate the performance of alarge number of tidal turbines. They used the LES turbulence model to compute the flow around six tidal turbines in an open water canal. The authors found that their approach is useful to find the optimum thrust values for the operating condition in order to maximize the output power of a farm of tidal turbines. Furthermore, the effect of hub-height (which is the distance between the seabed and the center of each of the turbines) has minor effect on the output power. Lloyd et al. [17] simulated a complete tidal turbine using the sliding mesh technique to connect the rotating and stationary flow domains. For this, they used the General Grid Interface (GGI) [18]. McNaughton et al. [19] simulated a flow around a tidal turbine and compared results with experimental results. The authors compared different turbulence models k-ϵ, k-ω (SST) and LES.
A good agreement for power and thrust coefficients as a function of Tip-Speed Ratio (TSR) was reported for all of turbulence models except the k- ϵ model. The LES turbulence model agreed best over a wide range of TSRs; the k- ω (SST) produced acceptable results and require less computational effort. Mason-Jones et al. [20] studied the effect of water depth on a tidal turbine. They showed that water depth has a great effect on the velocity profile, which affects the turbine performance. They compared their predictions to experimental results. The effect of increasing turbine diameter and flow velocity on power, torque and thrust coefficients were studied. The Reynolds number based on the outer turbine diameter did not exceed 5×105. Qi Wang et al. [21] used the RANSE solver to study the hydrodynamic characteristics of a tidal turbine in uniform flow with a multiple degree of motion. Gebreslassie et al. [22] developed an analytical approach to estimate flow profiles downstream of tidal turbines. They estimated the power extraction of a farm of tidal turbines and compared results to the results obtained by an ADM method. Based on their analytical approach, 91% of isolated turbine power could be developed by keeping a longitudinal axial distance of 20D between two turbines, where D is the turbine’s outer diameter. Brutto et al. [23] introduced an equation to estimate the wake radius of a tidal turbine. With their equations they found the average and the minimum velocities for the axisymmetric wake. That is valid for a turbine with a small diameter to depth ratio. Their diameter to depth ratio was 20%. They compared ADM method calculations to experiments. Their equations accurately predicted the velocity profile for the different I; however, the kinetic energy in a mixed wake could not be evaluated. Lam et al. [24] and Lam and Chen [25] derived analytical equations to predict wake velocity profiles based on the same method used in the wake shape of propellers. Results based on these equations compared favorably to experimental results. These analytical models are used frequently to analyze tidal turbine wakes. Analytical methods are efficient; however, they cannot study the flow around blades. el Sheshtawy et al. [37] designed a tidal stream turbine that uses one of the optimised hydrofoils, whose lift-to-drag ratio at an angle of attack of 5.2 degrees was 4.5% higher than that of the reference hydrofoil. The incompressible Reynolds-averaged Navier Stokes equations in steady state were solved using k-ω (SST) turbulence model for the reference and optimised tidal stream turbines. Thrust and power coefficients of the modelled reference turbine were validated against experimental measurements. The output power and thrust of the reference and the optimised tidal turbines were compared. el Sheshtawy et al. [38] carried out shape optimization of a tidal stream turbine hydrofoil to improve its output power. They developed a Matlab code to optimize the shape of its hydrofoil and coupled our code with a flow solver to determine the turbine’s performance.
In the present study, we focused on the use of the MRF method to simulate the flow around a tidal stream turbine in a homogenous flow and to compare results of the MRF method and ADM method of the wake flow behind the turbine at different turbulence intensities. The MRF method evaluated the forces acting on the tidal turbine blades and the optimum distance in the radial and longitudinal directions for tidal turbine farms. Furthermore, the forces acting on the turbine blades was calculated and used the MRF method.
2. Test Case
We analyzed the industrial three-bladed tidal turbine STG 50 [26]. The turbine rotor blades, made of carbon fibre composite material, were optimized based on size, giving them a high power to weight ratio and a low power to cost ratio. A high-power coefficient (CP) and a low the thrust coefficient (CT) in the overload conditions and minimal cavitation were also considered for optimization. A stall controlled system and a simple control system were used. The turbine was run at different rotational speeds and the power was recorded up to the rated power of the overall system.
The speed of the turbine was controlled to prevent the system from damage through overheating. The turbine diameter is 4 m, the hub diameter, 1.48 m, and the turbine nacelle length, 2.92 m, as shown in Figure 1. A model scale and full scale of STG 50 turbine were tested [26], the last one was performed using a tugboat as shown in Figure 2. The tugboat test has more advantages i.e. it can test the tidal turbine at different flow velocities in short time compared to offshore test. The data was collected using a sampling frequency 10 Hz. The tug test was done in the harbor of Rotterdam. The water density was 1022 kg/m3. As reported by the author, the effect of velocity shear and turbulence was not significant in that environmental test conditions. CP and CT were determined experimentally for different TSR, ranging from 1 to 9. The power and torque curves were determined for various flow velocities ranging from 1.75 to 3.5 m/s. The cut-in speed of the turbine occurred at a velocity of 0.9 m/s, the rated velocity equal 2.75 m/s and the maximum velocity is equal to 5.5 m/s. There was a reduction in thrust of approximately 50% at a velocity of 5 m/s. The STG 50 tidal turbine had a rated power of up to 50 kW at a TSR ratio of 4.5 evaluated at the rated velocity of 2.7 m/s.

3D model of the tidal turbine model STG 50. The black, the red and the blue colors represent the hub, blades, and the nacelle respectively.
3. Numerical Methods
The Open C++ library OpenFOAM, version 4 [27] was used to simulate the flow around the STG 50 tidal turbine, wherein RANSE equations for incompressible flows are solved based on the finite volume discretization method (FVM) [28]. The chosen solver C++ library OpenFOAM called simpleFoam, which uses the SIMPLE algorithm to solve pressure velocity coupling [29][30], was used.
3.1 Governing equations
We assumed steady state conditions of an incompressible Newtonian fluid and considered a fixed control volume (CV).
The integrated form of the steady state mass conservation (continuity) equation is:
| (1) |
where is the velocity vector of the fluid, S is the bounding surface of the control volume (CV) 129 and is the unit normal vector directing outwards. The momentum equations are
| (2) |
where ρ is the fluid density, p is the pressure, is the unit tensor, V is the volume, F is the volumetric body force and is the viscous stress tensor with components proportional to the deformation rates of the fluid and it defines as:
| (3) |
where μ is the dynamic viscosity of the fluid, xj refers to the Cartesian coordinates and ui refers to the Cartesian components of the velocity vector u. For more details, see [30].
3.2 The multiple reference frame (MRF) method
The MRF method divides the fluid domain into two steady-state zones, namely, a rotating zone and a stationary zone. In the stationary zone, the continuity equation is solved in the domain as Equation 1 and the momentum as vector Equation 2. In the rotating zone, the continuity equation is then,
| (4) |
based on the fluid relative velocity (), which is
| (5) |
where ω and x are the angular velocity and the position vector of a fluid element, respectively. The effect of the rotating domain is evaluated by adding the Coriolis and the centrifugal forces in the momentum Equation 2. The equation for the coordinate frame moving the volumetric body force is then,
| (6) |
where ao and ω are the acceleration of the coordinate system origin and the angular velocity vector describing the rotation of the coordinate system respectively. The first two terms will vanish if the system is moving with constant rotating velocity. The will replace the absolute velocity in Equation 2.
3.3 The actuator disk momentum (ADM) method
The ADM method [2] represents the rotor of a tidal turbine by a disc. The thrust and power coefficients are assumed to be homogeneously distributed on this disc. A pressure discontinuity and a reduction in the kinetic energy between the disc and the flow field is caused by the thrust force. CP is written as follows:
| (7) |
where P is the turbine output power, ρ is the fluid density, A is the turbine frontal area and U∞ is the free-stream velocity.
The moment coefficient Cm is written as follows:
| (8) |
Here M is the moment (with reference to the turbine axis) acting on the turbine and r is the turbine radius. The thrust coefficient CT is written as follows:
| (9) |
4. Numerical Methods
4.1 Computational domains
Figures 3(a) and 3(b) show the MRF computational domain and Figures 3(c) and 3(b), the ADM computational domain. The dimensions of the MRF and the ADM computational domains are shown in Table 1. The ratio between the downstream distance and the turbine outer diameter (Xd/Do) was set to 25 in order to study the effect of the turbine wakes.
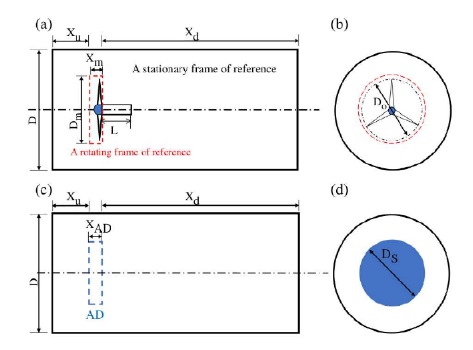
2D schematic drawing of the tidal turbine domain and dimensions: (a) side view and (b) frontal view of the MRF domain; (c) side and (d) frontal view of the ADM domain
4.2 The MRF Boundary conditions
Figures 4(a) and 4(b) show the MRF computational domain. Velocity, turbulent kinetic energy, and dissipation were imposed at the inlet boundary. A zero-pressure value was specified at the outlet boundary. A no-slip boundary condition was applied at the turbine blades and the domain walls. The computational domain size was chosen to avoid disturbance at the computational domain boundaries [31]. The angular velocity was imposed at the MRF zone. The TSR is written as follows:
| (10) |
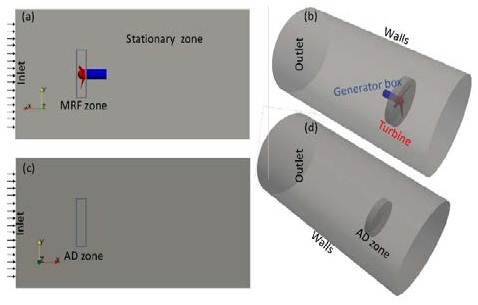
Tidal turbine domains. (a) The 2D domain sketch and (b) is the 3D sketch for the MRF domain. (c) The 2D sketch domain and (f) the 3D sketch for the ADM.
where n is the turbine’s revolutions per minute, Do is the turbine diameter, and U1 is the free stream velocity. We choose TSR values based on experimental results for a constant free stream velocity of 2.7 m/s as listed in Table 2.
We used inlet turbulence intensities (I) to estimate the domain initial conditions for different turbulence models [32]. The turbulence kinetic energy (K) was initially estimated [30] as follows:
| (11) |
the dissipation rate of the turbulence model is written as follows:
| (12) |
where l is the characteristic length equal to 0.07D = 1.82 m and the specific dissipation (ω)
| (13) |
The turbulence kinematic viscosity is defined for the k- ω turbulence model as follows:
| (14) |
and for the k- ϵ turbulence model as follows:
| (15) |
4.2 The ADM Boundary conditions
Figures 4(c) and 4(d) show the computational domain used for the ADM method. The boundary conditions for the inlet, the outlet and the walls are the same as for the MRF method. In this method, the experimental values of CT and CP at TSR (where CP is maximum) and A were prescribed before and has values as lists in Table 3.
5. Discretization Study and Validation
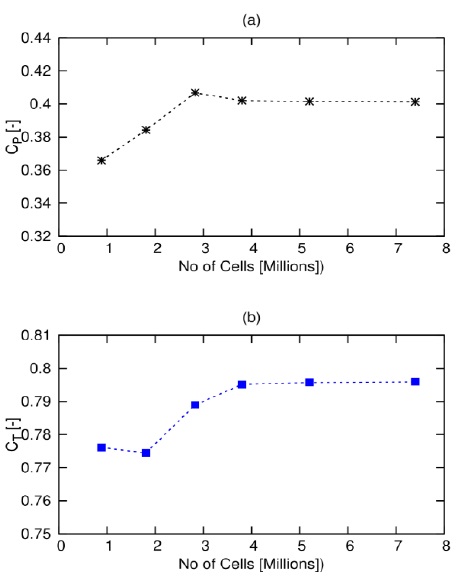
The SnappyHexMesh utility software OpenFOAM foundation (28; 33) was used to generate the for the MRF and the ADM computational mesh domains. The grid dependence study was performed for CP and CT. The averaged non-dimensional wall distance y+ value [30] was set to 200 at the surface of turbine blades for all meshes [31]. For case 4 in Table 2 (with the highest Cp), numerical simulations for the mesh dependence study were carried out. TSR was 4.5, turbulence intensity was 15%, and the turbulence model k-ω (SST) was used. Figure 5 shows the mesh topology. The results of the discretization study are presented in Figure 6. As shown in Figure 6(a), the deviation between computed Cp on the first and the second mesh is about 5%, between the second and the third mesh 5.86%, between the third and the fourth mesh -1.17%, between the fourth and the fifth mesh -0.134%, and between the fifth and the sixth mesh -0.05%. Figure 6(b) shows the grid study for CT. The deviation between the first and the second meshes is -0.21%, between the second and the third meshes is 1.87% and between the third and the fourth meshes is 0.78%, between the fourth and the fifth meshes is 0.071% and between the fifth and the sixth meshes is 0.03%. Based on these results, the numerical grid consisting of 3,798,394 control volumes seem to be fine enough to compare the ADM and MRF methods.

The mesh at different cross sections: (a) the mesh domain close to the MRF zone, (b) the meshing of the tidal turbine and (c) the mesh domain for the ADM method domain
6. Results
To recall, we used the MRF method to compute CP and CT coefficients of the STG 50 tidal turbine at the different TSRs, the forces that act on the turbine blades and the pressure distributions at each blade cross sections. Based on these findings, we calculated the optimum longitudinal and radial distance for a farm of STG 50 tidal turbines. We used the MRF and the ADM method to study the effect of I on the turbine wake behavior.
6.1 Power and thrust coefficients
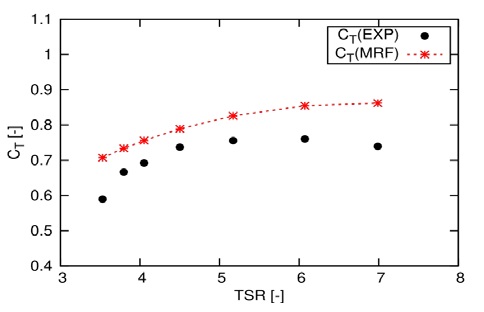
Figure 8 compares computed CP and Cm for different TSR values to corresponding experimentally data. We used the same turbulence intensity (I = 15%) as experimentally computed. Here, the maximum deviation between the computed and measured CP values for TSR between 3.5 and 4.5 was less than 1%. However, at TSR ranging from 5 to 7, the maximum deviation increased to 7.0%.
Figure 9 shows that the maximum relative error of CT is less than 10.0% for TSR values between 3.8 and 6.0, whereas for TSR values between 6.0 and 7.0, the maximum deviation increases to 16.5%. However, for relatively high TSR values, the difference between the numerical and experimental results increases, possibly because of separated flow on the turbine. Most tidal turbine designs operate within the highest CP values to extract the maximum output power from the turbine by active pitch control [36] or by changing the turbine revolutions relative to the free-stream velocity, whereby the TSR remains fixed to corresponding to the highest CP value. We achieved the highest CP value at TSR = 4.5. Here, the maximum deviation was -0.11% for CP and 7.0% for CT. Therefore, we performed all our simulations at a TSR = 4.5.
6.2 Turbine blade load analysis
The forces and the moment or the torque acting on a single blade were computed using the MRF method. A blade subdivided into twenty segments, forces, and momentum at the center point of each segment were evaluated by integrating the pressure and the skin-friction forces over a single blade. Figure 10(a) illustrates the normalized force, Fn/Fto, which acted normal to the local chord axis of a blade, and the normalized tangential force, Ft/Fto, which acted along the local chord axis versus the normalized radius (r/Ro). Forces were evaluated at TSR = 4.5 and I = 15%. These blade forces were normalized against the maximum tangential force Fto acting on the blade. The Fn/Fto increase on the blade until it reached its maximum at 0.8R (equivalent to 1065.3 N) and then decreased. Meanwhile, the Fn/Fto ratio increased until it reached its maximum at the same operating point (equivalent to 400 N) and then decreaseds. Figure 10(b) illustrates the normalized torque (Mo) relative to the maximum torque (Mxo) acting on the blades and on the hub, which also increased until it reached its maximum at 0.9Ro (equivalent to 382.3 N.m) and then decreased. Maximum stresses on the turbine blade occurred at turbines radius between 0.8 and 0.9Ro. Figure 11 shows the pressure distribution at r/Ro ratios of 0.3, 0.5, 0.8 and 0.9. Towards the tip, the pressure drop increased to -40 kPa at r/Ro = 0.9. Figure 12 shows the pressure distribution on the turbine pressure side and the suction side of all three blades and the hub. The pressure decreased towards the tip and reaches -40 kPa.
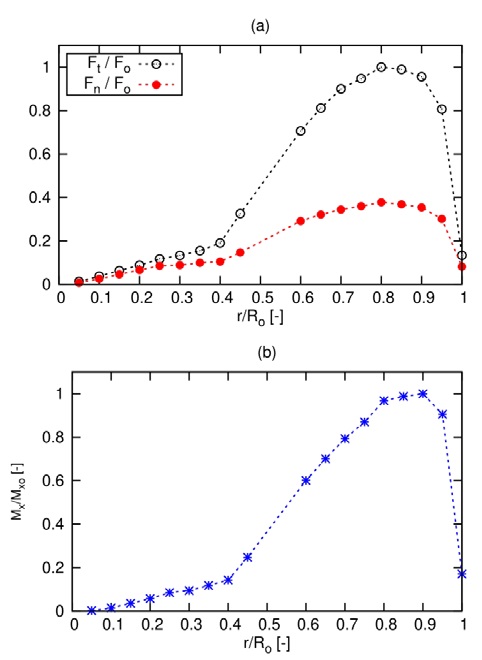
Forces acting on a single blade of the tidal turbine at TSR = 4.5 and I = 15%; (a) refers to the Fto and the Fn versus r/Ro, while (b) refers to the Mx versus the r/Ro
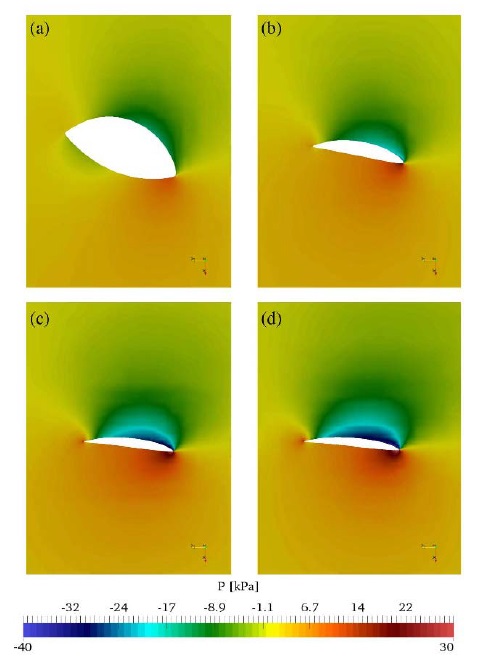
The absolute pressure distributions around different sections of the turbine blade at TSR = 4:5 and I = 15%: (a) r=Ro = 0:3, (b) r=Ro = 0.5, (c) r/Ro = 0.8 and (d) r/Ro = 0.9.
6.3 Flow surrounding the turbine
In this section the flow around the STG 50 turbine blades was studied by the MRF method. The optimum radial distance (from which no velocity interference) occured between the turbines in a farm of turbines when evaluated. Normalized velocities (U/U∞) for free-stream velocity (U∞) equal to 2.7 m/s were taken at four longitudinal distances from the inlet (X) as shown in Figure 13 (a). As shown in Figure 14, the greatest velocity diffusion occured at X1 = 10.8 m. With increasing X, velocity diffusion decreased.

Computational domain: (a) is the side view with four different cross sections, (b) is the front view with the radial line at angle equal to 45
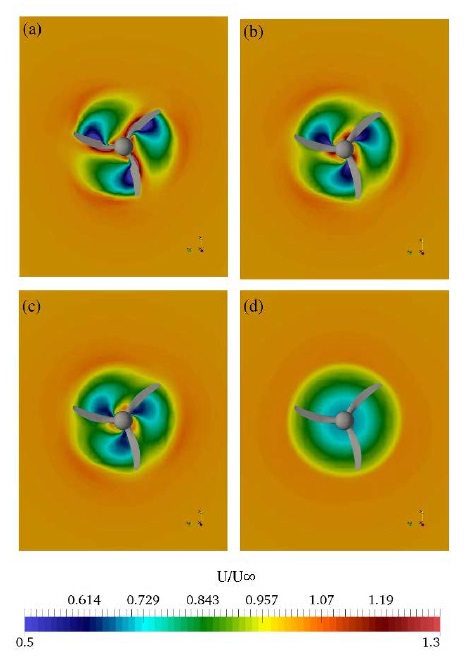
Normalized velocity U/U∞ at different cross sections at TSR = 4.5 and I = 15%: (a) X1 = 10.8 m, (b) X2 = 11.0 m, (c) X3 = 11.1 m and (d) X4 = 12.6 m.
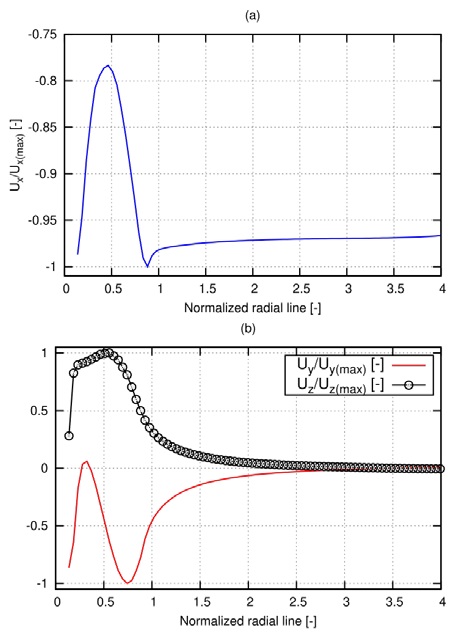
The velocity diffusion enlarges the velocity disturbance in the radial direction. This velocity disturbance may affect the performance of other turbines in a tidal turbine farm, and therefore we studied the velocities in the radial direction. The four contour plots show that the fluid flow around the three blades is symmetrical as expected. The flow (in case of a turbine operating in homogeneous flow) may be computed in the third of the computational domain using cyclic boundary conditions. This consequently save computational time. In Figure 15, the normalized velocities in x, y and z directions are plotted along the normalized turbine radius (r/Ro) at X1 = 10.8 m. Figure 15(a) shows the normalized velocity in x direction relative to the maximum velocity in the same direction (Ux/Ux(max)), Ux(max) is 2.85 m/s in this case. The effect of the turbine on the velocity in x direction ended approximately at R/Ro = 2.5 where to Ux/Ux(max) was almost constant. The negative sign of this value indicates only its direction. Figure 15(b) shows the normalized velocities in y and z directions relative to the maximum velocity compare the regarded direction (Uy/Uy(max) and Uz/Uz(max) respectively), in this case, Uy(max) is 0.277 m/s and Uz(max) is 0.361 m/s. The effect of the turbine on the velocities in y and z directions ends approximately at R/Ro = 3.0 corresponding to Uy/Uy(max) and Uz/Uz(max) values equal to zero. We conclude that a farm of STG 50 turbines, which gives the maximum output power for each turbine, can be arranged, with the turbines being separated by three times the turbine’s radius.
6.4 Velocity distribution
For more efficient power extraction from tidal energies, tidal turbine works in a farm of turbines. In this section and the following sections, we will study the flow behavior behind the tidal turbine such as the velocity distribution, turbulence intensity distribution, and the wake width behind the turbine. In this section, we will study that the velocity deficit distributions (UD) of the turbine at TSR = 4.5 were evaluated for the MRF and ADM simulations. UD is defined as follows:
| (16) |
where U is the is the wake velocity in the streamwise direction and U∞ is the streamwise flow velocity.
Figure 16 shows that the red dotted lines define normalized distances Xd/Do, which represents the coordinates at which UD values were calculated on it in Figure 17. The blue dotted lines define the normalized radial distance D/Do, which represents the coordinates at which UD values were calculated on it in Figure 18.
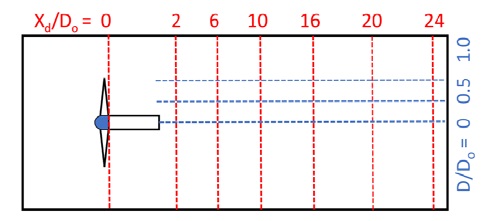
2-D sketch for the turbine domain, where blue dotted lines represent 0, 0.5 and 1.0 D/Do. The red dotted lines represent 2, 6, 10, 16, 20 and 24 Xd/Do respectively
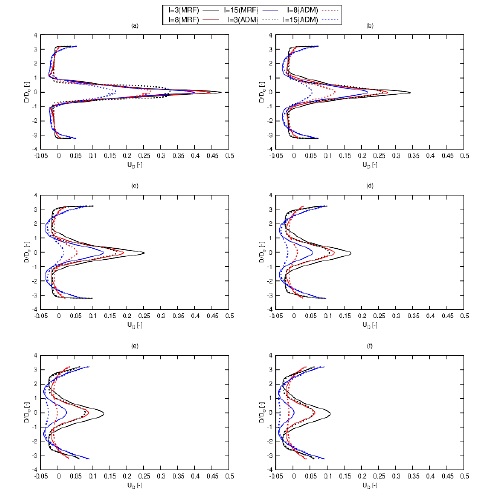
Velocity deficit distributions along the Xd/Do: (a) 2, (b) 6, (c) 10, (d) 16, (e) 20, (f) 24 at TSR =4.5 and different I using the MRF and the ADM methods
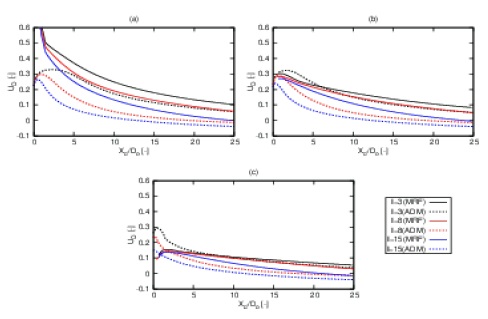
Velocity deficit distributions along with the D/Do: (a) 0, (b) 0.5, (c) 1 at TSR =4.5 and the different I using the MRF and the ADM methods
Figure 17 shows the result that UD at the normalized longitudinal distance (Xd/Do) equals to2, 6, 287 10, 16, 20 and 24 for different values of I. As Xd/Do increased, UD decreasedand shifted its maximum toward the turbine. As I increased, UD was reduced close to the turbine axis of rotation. We conclude that for a farm of STG 50 tidal turbine, the staggered pattern is more efficient in turbine working condition that inline pattern. Figure 18 presents the result that UD values at D/Do equal to 0, 0.5, and 1 at I equal to3, 8, and 15 %. As the value of UD close to zero means that the velocity is equal to steam velocity. At D/Do = 0 at the axis of turbine, the value of UD is the highest as shown in Figure 18(a). The value of UD decreased as we increased the D/Do values as shown in Figures 18 (a) and (b).
The value of UD reached to value of 0.1 at Xd/Do equal to 25 for all method which is enough for good operating condition for the next row of turbines. We conclude that a staggered pattern of a farm of STG 50 tidal turbine should be at D/Do between 0.5 and 1, and Xd/Do equal to 25.
6.5 Turbulence intensity distributions
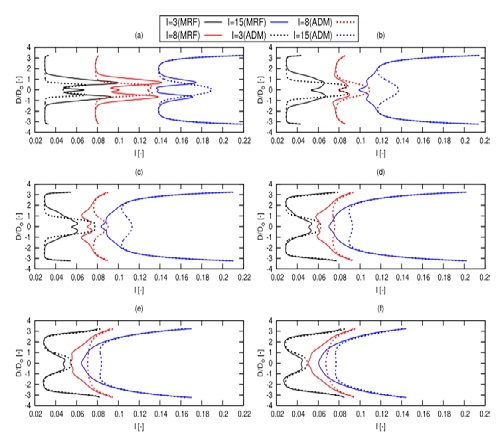
Figure 19 shows distributions of Turbulence intensity (I) along with the normalized radial distance (D/Do) at Xd/Do = 2, 6, 10, 16, 20 and 24. At Xd/Do = 2 and I = 3%, Xd/Do = 6, 10 and 16, and Xd/Do = 20 and 24, the results were close to each other except at the center of the turbine’s fluid domain. At Xd/Do = 2 and I = 8%, the I distribution width from the ADM method is less than the I distribution from the MRF method. However, at Xd/Do = 6, 10, 16, 20 and 24, the width of I distribution were the same.
2-D sketch for the turbine domain, where blue dotted lines represent 0, 0.5 and 1.0 D/Do. The red dotted lines represent 2, 6, 10, 16, 20 and 24 Xd/Do respectively.
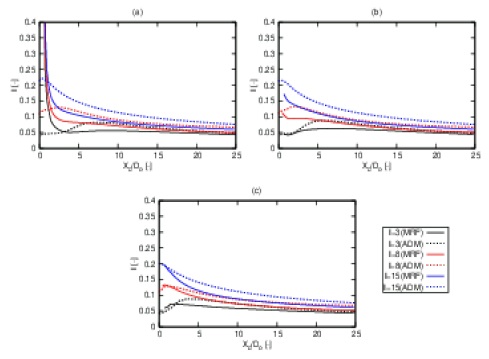
I distributions along the normalized Xd/Do at different D/Do: (a) 0, (b) 0.5, (c) 1 at TSR = 4.5 using the MRF and the ADM methods.
The I distribution width from the ADM method was almost the same as the I distribution from the MRF method, but they were less than the I distribution close to the turbine’s fluid domain. The MRF method predicted the I distribution more favorably than the ADM method. Figure 21 shows the contour plots of UD for TSR = 4.5 and I = 15% at different cross sections. These contours show the decrease of the width of the wake (W) as going far from the turbine.
6.6 Wake width
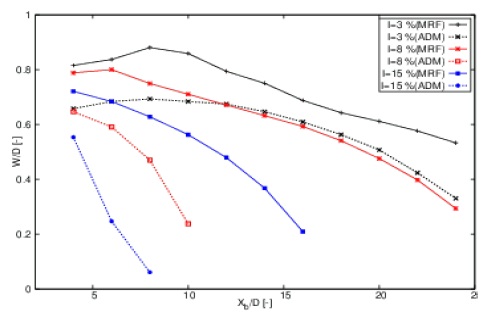
As shown in Figure 22, we calculated the normalized wake width (W/Do) at U = 0.95 U∞ and U = 0.05 U∞ for different values of I according to [9]. The wake width is important because it affects the longitudinal distances between adjacent turbines.
7. Computational time
All numerical simulations were performed on a workstation with an Intel Xeon Processor E3- 316 1241v3 @ 3.50 GHz, 8 M Cache and 32 Gb Ram memory. On average, the simulation using the MRF method lasted 47.58 hours, and that using the ADM method lasted 44.78 hours on eight 318 processor cores. This comparison is based on using about the same number of 3,798,394 cells 319 and the same number of 5000 iterations for the both methods.
8. Conclusion
We used the MRF method to study the flow surrounding a tidal turbine and the behavior of the wake domain behind it, including the blade forces and the pressure distributions acting on the turbine. We compared the results of the wake behind the tidal turbine of the ADM method and the MRF method. We examined the influence of the turbulence intensity on the wake velocities and the wake widths by setting it to 3, 8 and 15% and compared our computed power and thrust coefficients to experimental measurements. We obtained out the best overall agreement results using the k-ω (SST) turbulence model. For TSR values between 3.5 and 6.0, the power and thrust coefficients deviated from experimental measurements results by less than 10%. Normal and tangential forces evaluated along with a single turbine blade attained with their maximum values at 0.8R. For TSR values of 4.5, the radial cross flow effect ended at the radius equal to three times the STG 50 tidal turbines radius. Furthermore, an increase of the turbulence intensity caused the velocity deficit close to the turbine to decrease. Increasing the turbulence intensity caused the wake width to decrease and the wake recovery to increase. We found the optimum radial and longitudinal distances for installing other turbines to produce optimum power output. Computational times for the ADM and the MRF methods under the same conditions were nearly equal.
Acknowledgments
This research was supported by the institute of Ship Technology, Ocean Engineering and Transport Systems, University of Duisburg-Essen.
Author Contributions
Conceptualization, H. el Sheshtawy; Methodology, H. el Sheshtawy; Software, Formal Analysis, H. el Sheshtawy; Investigation, H. el Sheshtawy; Visualization, H. el Sheshtawy; Writing-Original Draft Preparation, O. el Moctar: Writing-Review & Editing, O. el Moctar: Supervision, O. el Moctar.
References
-
A. M. Gorlov, Tidal Energy, Northeastern University, Boston, Massachusetts, USA, 2001.
[https://doi.org/10.1016/B978-012374473-9.00032-1]

- G. Houlsby, S. Draper, and M. Oldfield, Application of Linear Momentum Actuator Disc Theory to open Channel Flow, University of Oxford, Oxford, U.K., 2008.
-
Ragheb, M., and Ragheb, A. M. Wind turbines theory-the betz equation and optimal rotor tip speed ratio. Fundamental and advanced topics in wind power, Illinois, USA, 2011.
[https://doi.org/10.5772/21398]

-
M. Shives and C. Crawford, “Tuned actuator disk approach for predicting tidal turbine performance with wake interaction,” International Journal of Marine Energy, vol. 17, pp. 1-20, 2017.
[https://doi.org/10.1016/j.ijome.2016.11.001]

-
V. T. Nguyen, S. S. Guillou, J. Thibot, and A. S. Cruz, “Modelling turbulence with an actuator disk representing a tidal turbine,” Renewable Energy, vol. 97, pp.625-635, 2016.
[https://doi.org/10.1016/j.renene.2016.06.014]

-
S. Pope, Turbulent Flows, Cambridge University Press, 2000.
[https://doi.org/10.1017/CBO9780511840531]

-
M. A. Abolghasemi, M. D. Piggott, J. Spinneken, A. Vire, C. J. Cotter, and S. Crammond, “Simulating tidal turbines with multi-scale mesh optimization techniques,” Journal of Fluids and Structures, vol. 66, pp. 69-90, 2016.
[https://doi.org/10.1016/j.jfluidstructs.2016.07.007]

-
M. G. Gebreslassie, S. O. Sanchez, G. R. Tabor, M. R. Belmont, T. Bruce, G. S. Payne, I. Moon, Experimental and CFD analysis of the wake characteristics of tidal turbines,” International Journal of Marine Energy, vol. 16, pp. 209-219, 2016.
[https://doi.org/10.1016/j.ijome.2016.07.001]

-
T. Blackmore, W. M. J. Batten, and A. S. Bahaj, “Influence of turbulence on the wake of a marine current turbine simulator,” Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences,” vol. 470, 2014.
[https://doi.org/10.1098/rspa.2014.0331]

- A. Jeromin, Bentamy, A., and Schaffarczyk, A. Experimental and computational analysis of a model horizontal axis tidal turbine. In First Symposium on OpenFOAM in Wind Energy, 20th/21th March, 2013.
- Ingram, Grant. "Wind turbine blade analysis using the blade element momentum method. version 1.1." Durham University, Durham, 2011.
- Fluent. Ansys fluent theory guide. ANSYS Inc. USA, http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf, , 15.10.2020.
-
W. X. M. Koh and E. Y. K. Ng, “A CFD study on the performance of a tidal turbine under various flow and blockage conditions,” Renewable Energy, vol. 107, pp. 124-137, 2017.
[https://doi.org/10.1016/j.renene.2017.01.052]

-
T. Nishino and R. H. J. Willden, “Effects of 3-D channel blockage and turbulent wake mixing on the limit of power extraction by tidal turbines,” International Journal of Heat and Fluid Flow,” vol. 37, pp. 123-135, 2012.
[https://doi.org/10.1016/j.ijheatfluidflow.2012.05.002]

-
W. Hunter, T. Nishino, and R. H. J. Willden, “Investigation of tidal turbine array tuning using 3D Reynolds-Averaged Navier Stokes Simulations,” International Journal of Marine Energy, vol. 10, pp. 39-51, 2015.
[https://doi.org/10.1016/j.ijome.2015.01.002]

- Nishino, Takafumi, and Richard HJ Willden. "Energetics of marine turbine arrays-extraction, dissipation and diminution." arXiv preprint arXiv:1308.0940, , 2013.
- Lloyd, Thomas P., Stephen R. Turnock, and Victor F. Humphrey. "Unsteady CFD of a marine current turbine using OpenFOAM with generalised grid interface." 2011.
- Beaudoin, Martin, and Hrvoje Jasak. "Development of a generalized grid interface for turbomachinery simulations with OpenFOAM." Open source CFD International conference. Vol. 2. Berlin, 2008.
-
J. McNaughton, I. Afgan, D. D. Apsley, S. Rolfo, T. Stallard, and P. K. Stansby, “A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal stream turbine,” International Journal for Numerical Methods in Fluids, vol. 74, no. 4, pp. 250-269, 2014.
[https://doi.org/10.1002/fld.3849]

-
A. Mason-Jones, D. M. O’Doherty, C. E. Morris, T. O. O’Doherty, C. B. Byrne, and et al., “Non-dimensional scaling of tidal stream turbines,” Energy, vol. 44, no. 1, pp. 820-829, 2012.
[https://doi.org/10.1016/j.energy.2012.05.010]

-
S. Wang, K. Sun, G. Xu, Y. Liu, and X. Bai, “Hydrodynamic analysis of horizontal-axis tidal current turbine with rolling and surging coupled motions,” Renewable Energy, vol. 102, Part A, pp. 87-97, 2017.
[https://doi.org/10.1016/j.renene.2016.10.036]

- Gebreslassie, Mulualem G., Michael R. Belmont, and Gavin R. Tabor. "Comparison of analytical and CFD modelling of the wake interactions of tidal turbines." 10th European Wave and Tidal Energy Conference (EWTEC2013), 2013.
-
O. A. Lo Brutto, V. T. Nguyen, S. S. Guillou, and et al., Tidal farm analysis using an analytical model for the flow velocity prediction in the wake of a tidal turbine with small diameter to depth ratio, Renewable Energy, vol. 99, no. 4, pp. 347-359, 2016.
[https://doi.org/10.1016/j.renene.2016.07.020]

-
W. -H. Lam, L. Chen, and R. Hashim, “Analytical wake model of tidal current turbine,” Energy, vol. 79, pp. 512-521, 2015.
[https://doi.org/10.1016/j.energy.2014.11.047]

-
W. -H. Lam and L. Chen, “Equations used to predict the velocity distribution within a wake from a horizontal-axis tidal-current turbine,” Ocean Engineering, vol. 79, pp. 35-42, 2014.
[https://doi.org/10.1016/j.oceaneng.2014.01.005]

-
P. Jeffcoate, R. Starzmann, and et al., “Field measurements of a full scale tidal turbine,” International Journal of Marine Energy, vol. 12, pp. 3-20, 2015.
[https://doi.org/10.1016/j.ijome.2015.04.002]

- OpenFOAM. user guide. OpenFOAM Foundation Ltd, version, https://cfd.direct/openfoam/user-guide, /, 20.10.2020.
- Jasak, H., Jemcov, A., and Tukovic, Z, OpenFOAM: A c++ library for complex physics simulations, In International workshop on coupled methods in numerical dynamics, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.453.9673&rep=rep1&type=pdf, , 20.10.2020.
- Patankar, S. V. Computational Methods for Fluid Dynamics. 9th Indian Reprint, Taylor& Francis, Germantown, NY, USA, 2016.
- Ferziger, J. H. and Peric, M. (2012). Computational Methods for Fluid Dynamics, , Springer, Heidelberg, Germany, 2012
- el Moctar, O. Numerical computations of flow forces in ship manoeuvring. Ship Technology Research, Numerical computations of flow forces in ship manoeuvring, 21.10.2021.
- Holzinger, G. Openfoam a little user-manual, https://www.cfd-china.com/assets/uploads/files/1621928562433-openfoam-user-manual-pfm.pdf, , 21.10.2020.
- Gisen, D. Generation of a 3d mesh using snappyhexmesh featuring anisotropic refinement and near-wall layers. https://docplayer.net/38027377-Generation-of-a-3d-mesh-using-snappyhexmesh-featuring-anisotropic-refinement-and-near-wall-layers.html, , 21.10.2021.
-
Shih, Tsan-Hsing, et al. "A new k-ϵ eddy viscosity model for high reynolds number turbulent flows." Computers & fluids 24.3 (1995): 227-238.
[https://doi.org/10.1016/0045-7930(94)00032-T]

-
F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications,” AIAA Journal, vol. 32, no. 8, pp. 1598-1605, 1994.
[https://doi.org/10.2514/3.12149]

-
W. Lam, and et al., “A review of the equations used to predict the velocity distribution within a ship’s propeller jet,” Ocean Engineering, vol. 38, no. 1, pp. 1-10, 2011.
[https://doi.org/10.1016/j.oceaneng.2010.10.016]

-
H. el Sheshtawy, O. el Moctar, T. E. Schellin, and S. Natarajan, “Numerical investigation of an optimised horizontal axis tidal stream turbine,” International Conference on Offshore Mechanics and Arctic Engineering, pp. V010T09A004, 2019.
[https://doi.org/10.1115/OMAE2019-95722]

-
H. el Sheshtawy, O. el Moctar, and S. Natarajan, “Multi-point shape optimization of a horizontal axis tidal stream turbine. Eng, vol. 2, no. 3, pp. 340-355, 2021.
[https://doi.org/10.3390/eng2030022]