Effects of blade number and draft tube in gravitational water vortex power plant determined using computational fluid dynamics simulations

1. Introduction

In recent times, the development of gravitational water vortex power (GWVP) technology has been very rapid, with much research being conducted regarding optimization of the vortex basin and turbine designs. The reason for the advanced development of this technology is the sustainability of the GWVP plant compared to other commercial small-scale hydropower extraction methods. Thus, vortex power plant designs can be adapted to suit a wide range of flow conditions involving smaller hydraulic heads. As the power plant design is a run-of-the-river system, no water storage reservoir is required, thus minimizing the environmental impact [1]. In addition, it can ensure water purification by aeration by increasing the oxygen concentration of the water [2]. On the other hand, this technology can be implemented in hillside areas enriched with hydro-potential to power up rural communities that are situated far away from the electricity distribution grid. Therefore, GWVP plants can be used to support rural communities, thereby providing social benefits [3]. Thus, the installation and maintenance of a GWVP plant is simple and cost-effective [4]. Therefore, according to the three pillars of sustainability (economic, environmental, and social), GWVP plants are a viable solution in the hydropower extraction sector. Franz Zotlöterer implemented the vortex power extraction method using the basic concept of Viktor Schauberger, which utilizes the natural energy stored in the water to form vortexes [5]. Initially, Zotlöterer used a water vortex to aerate the water without employing any external power. Later, he used a vertical axis rotor at the vortex center to generate rotary energy [6].

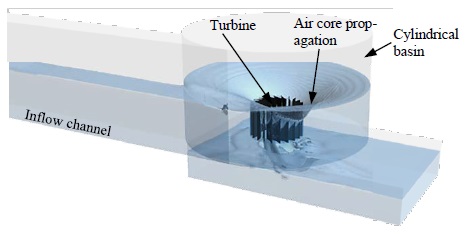
In the GWVP plant, gravity-driven water is guided in a tangential direction to a circular basin structure called a vortex basin with a bottom center outlet. Therefore, inside the vortex basin, water creates a strong vortex around the vertical-central axis. Using the vertical axis turbine, the vortex power generated can be extracted as mechanical energy and later converted to electrical energy through the use of generators. Figure 1 illustrates the GWVP plant design used in this study, showing the main components. The vortex basin and vortex turbine are the main components of a GWVP plant. Therefore, the GWVP plant design is developed mainly by optimizing the structure of the vortex basin or the design of the vortex turbine. Although several studies have been conducted using various optimization procedures, GWVP technology is accepted as a relatively new technology, as no standard design procedure is available.

Figure 1:

GWVP plant design

Dhakal et al claimed that the design of the conical shaped vortex basin performs better in terms of efficiency than the cylindrical basin, in the same position of the turbine [7]. It is recommended that the water flow from the inlet channel to the basin be as tangential as possible because it causes fewer distortions and prevents unnecessary losses [8][9]. The inlet design of most vortex basins is either tangential or scroll with a flat bottom. The scrolling inlet is more commonly used as it increases the discharge gradually, spiraling along the basin towards the drain outlet [10]. Thus, for a cylindrical-shaped basin, Choi et al suggested a ratio for the optimal bottom outlet orifice diameter to basin diameter in the range of 17-18.5% [11]. The vortex strength and stability depend greatly on this diameter ratio, with the formation of a central air core [12]. Smaller diameter ratios block the outlet, thus preventing air core formation, while the ratios for larger diameters release water without circulation. In both cases, it tends to reduce the vortex strength [10].

The vortex turbine is closer to the impulse-type turbine than to the reaction-type turbine because it does not work on the pressure differential, but rather on the dynamic force of the water vortex [2][13]. When the turbine is inserted into the vortex basin, the vortex is disturbed by the turbine blades, thus decreasing the tangential velocity component of the water while increasing the axial velocity component [2][14]. Several studies have been conducted to optimize the blade profile geometry. Dhakal et al [15] demonstrated that a horizontal curved blade profile was the most efficient. However, Saleem et al [14] reported low performance for horizontal curved blades because the tangential velocity component that was affected resolved into components, and only one component contributed to the blade rotation. In fact, Bajracharya et al [16] studied the effect of several blade parameters on turbine performance in terms of the impact angle, blade angle in the vertical and horizontal planes, taper angle, height, cutting of the blade, and number of blades. The study is concluded by recommending a ratio of 0.31-0.32 blade height to basin height, 20° impact angle, and taper angle conforming to the basin cone angle and blade at a horizontal angle of 50° to 60°.

The bottom-most position inside the vortex basin is accepted as the best place to locate the turbine in a conical basin because the vortex strength is at its highest at the drain orifice [13][17]. Dhakal et al [17] claimed a decline in the performance when the number of blades in the turbine increased from six to 12; however, Christine Power et al [18] claimed heightened performance when the number of blades was increased from two to four. The number of blades or guide vanes is one of the most important parameters in the design of hydro turbines [19]. The optimal number of blades in a vortex type turbine depends on the strength of the formed vortexes and several other factors, especially the friction losses. Generally, in vortex phenomena, the air-core radius decreases gradually from the free surface to the bottom orifice [20][21]. However, in the presence of the turbine, the air core behavior becomes more complex. Furthermore, a larger turbine hub diameter is not recommended because it tends to disturb the air core formation and the vortex shape without gaining power [14]. Finally, more complicated flow behavior occurs inside the GWVP plant, influenced by many factors [12], especially the behavior of the air core and friction losses.

The GWVP plant in this study was designed based on the findings of the studies cited above, while adapting them for a selected installation site. As one of the objectives of the current study, the CFD flow field was observed to identify the effect exerted by the number of blades in the vortex turbine, while improving the conical basin design provided with a small draft tube. Computational fluid dynamics (CFD) was extensively used in this study to simulate and analyze the flow field in each case, with an assessment of the performances.

In the first section of this article, the GWVP plant is introduced with a brief literature review on past researches; in the second section, the fundamental concept regarding the vortex theory and water velocity behavior in the GWVP plant is explained. In the third section, the methodology, computational design, and simulation procedure are described. In Section four, the performance curves for different numbers of blades and draft tube cases are presented. Validation of the CFD setup is discussed, as this study was based on CFD simulations. Finally, in Section five, the simulated flow fields are analyzed using the water-air interface, velocity vector, and pressure contour. Hence, utilizing the flow phenomenon, the variations in performance are justified and discussed. In Section six, the conclusions of the study are presented, citing the findings of the current study along with suggestions for improvements.

2. Vortex Phenomena and Vortex Turbine

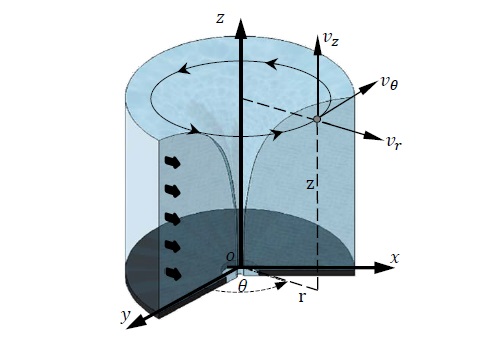
The formation of the water vortex is explained by applying the angular momentum theory [10]. A fluid particle with a small angular velocity but with a large radial position produces a significant angular momentum. When the particle moves toward the center, it gradually reduces the radial position while increasing the angular velocity to conserve the angular momentum. Therefore, at the central axis, the water flow creates a significant swirl, called the vortex. Vortex systems are normally discussed in terms of cylindrical coordinates, where the center axis is laid along the z axis and the velocity vectors v_r, v_θ, v_z correspond to the radial (r) , tangential (θ) and axial (z) directions as shown in Figure 2.

Figure 2:

Cylindrical co-ordinate system used to describe the vortex phenomena

By solving the Navier-Stokes equation in continuity and three momentum equations with the assumption of steady, asymmetric, and inviscid flows with axial derivatives as negligibly small, the tangential momentum equation is simplified to the relationship given below for the potential vortex shown in Equation 1.

where Γ is the circulation, defined as the line integral of the tangential velocity component.

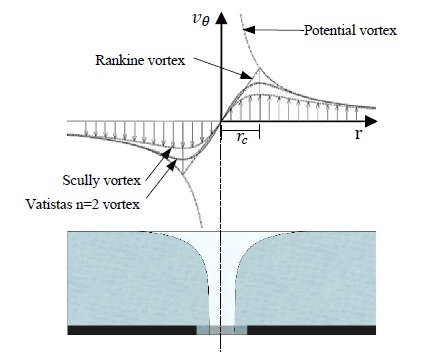
Therefore, in a vortex system, the tangential velocity component dominates the flow field, where the radial and axial velocity components are negligible. As the potential vortex model is not suitable for describing the center of the vortex, Rankine proposed a more reliable model, which was later used by many professionals for the development of reliable vortex models. In Figure 3, the different vortex models followed by the Rankine and potential vortex models are depicted. Furthermore, an air core was formed at the center of the free-water vortex. The water vortex stability depends on the formation of a continuous stable air core [10].

Figure 3:

Tangential velocity variation for different vortex models

When the vertical-axis turbine is placed in the water vortex field, the vortex is distorted by the turbine blades that extract the vortex energy. The tangential velocity component of the vortex contributes substantially to the power extraction, as it is the dominant velocity component in the vortex. Initially, the vortex is struck on the turbine blades, reducing its tangential velocity components, while slightly increasing the axial and radial velocity components. The vertical twisted blade profile of the turbine was used to extract the excess energy from the axial velocity component just prior to discharge.

As the energy is extracted chiefly from the tangential velocity component of the water vortex, it is important to identify the effect of the number of blades. The number of blades in the vortex turbine is strongly dependent on the strength of the vortex, where the distance between the blades must be effective for receiving the power of the water flow onto the blades [5]. Therefore, as one objective of this study, an optimal number of blades was identified in the vortex turbine while observing the behavior of the CFD flow. Another aspect of this study involved the analysis of the effect of different draft tube designs as an extension of the modification of the vortex basin.

3. Design and Computational Modelling

3.1 Methodology

The design of the GWVP plant is highly dependent on recent research findings and the site conditions, particularly the space availability, flow, and hydraulic head. The design was developed to recover the energy of wastewater discharged from a fish farm located in the area called Namhae, on the southern coast of South Korea. The average flow rate was recorded as 0.530 m³/s, and the estimated hydraulic head was 2 m.

To compare the GWVP plant parameters, a three-dimensional structural model was created for the vortex basin and turbine. Using the structural model, the fluid domains were extracted for CFD simulations. As the CFD is based on finite element theory, the fluid domains were meshed using ANSYS ICEM software. Then, the fluid domains were set up in ANSYS CFX to define the necessary boundary conditions. As this research is strongly based on the CFD study, the validation process was initially performed by comparing it with the experimental results of a recent GWVP plant research, showing fair agreement.

In this study, two main cases related to the vortex turbine and basin were analyzed. Under the effect of the number of blades, four different cases were simulated having 5,6,8 and 10 blades. Selecting the best turbine (with the most effective number of blades) as the optimal turbine, the draft tube cases were further studied. The effect of the draft tube was observed under four specific cases: no draft tube, straight draft, conical draft tube, and height increased conical draft tube.

Hydraulic efficiency was used as the criterion to compare the performance of the GWVP plant, which is denoted by the ratio of the extracted power to the available hydraulic power, as expressed in Equation 2.

$\[ \eta =\frac{P_{extracted}}{P_{available} } \]$

(2)

Generally, the available hydraulic power is calculated using Equation 3,

$\[ P_{available}=\rho gQH \]$

(3)

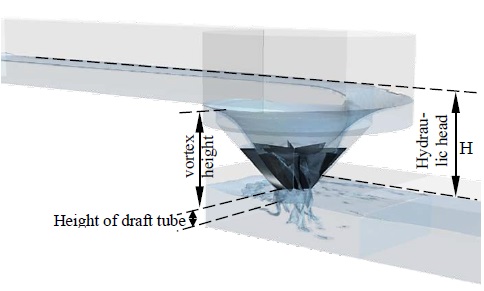
where ρ is the density of water (998 kg/m3), g is the gravitational acceleration (9.81 m/s²), Q is the volume flow rate, and H is the hydraulic head, which is defined as the difference between the inflow and outflow water level but not related to the vortex height. H was calculated using the CFD post-processing, as shown in Figure 4.

Figure 4:

Hydraulic head and the maximum vortex height inside the designed vortex basin

Extracted power is calculated using the Equation 4.

$\[ P_{extracted}=\tau \omega \]$

(4)

where τ is the torque on the turbine in Nm, which is monitored during the CFD solving process. ω denotes the rotational speed of the turbine in rad/s, which was predefined in the simulations.

3.2 Computer aided modeling

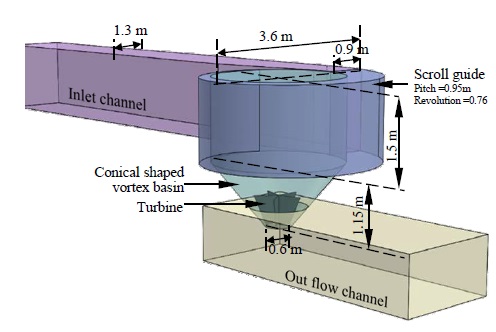
The width of the wastewater discharge channel is 1.3 m, at the selected site. Considering it as the inflow channel to the GWVP plant, this channel was made to converge to the vortex basin via a scroll guide channel. Therefore, to facilitate the entry of water into the conical-shaped part of the basin, the upper part of the vortex basin was designed with a flat bottom. The maximum diameter of the vortex basin was 3.6 m and the diameter of the bottom discharge orifice was 0.6 m. Different draft tube designs were then fitted to the drain orifice. Three types of draft tube cases were observed: straight, conical, and increasing the conical height, followed by no usage of the draft tube. In Figure 5, the basic fluid model for the designed GWVP plant is illustrated, and Figure 6 shows the difference between each of the simulated draft tube designs. Although the estimated water height is 2 m, the model was extended further, allowing it to adapt to the height of the water level for different rotational speeds. An outlet channel was designed to observe discharge water flow after draining out from the basin.

Figure 5:

CAD model for designed vortex basin fluid domains

Figure 6:

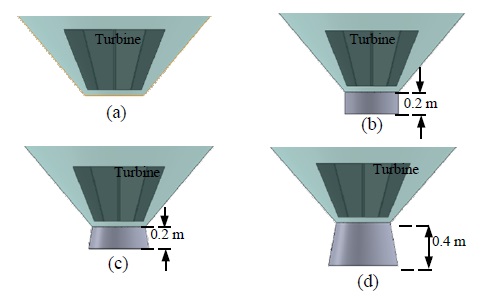
Different draft tube designs (a) no draft tube (b) straight draft tube (c) conical draft tube- divergent angle 10° (d) height increased conical draft tube

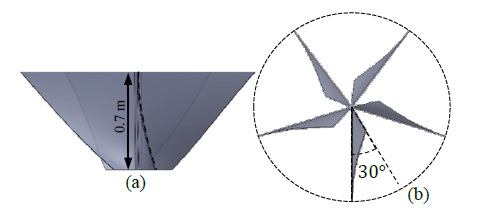
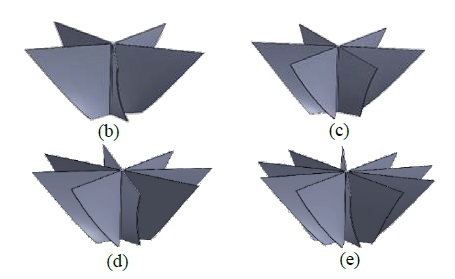
The basic vortex turbine model was designed to have five vertical twisted blades matched with a conical shaped basin, having 0.7 m height. The twist angle was 30° between the top and bottom blade profiles, where the twist was gradually increased from the top to the bottom of the blade. In Figure 7, the basic turbine denoting the parameters of the blade profile is illustrated, whereas in Figure 8 the 5,6,8 and 10 bladed turbines are shown. The turbine hub diameter was maintained at 50 mm for every case, and the gap between the inner wall of the basin and the blade tip was maintained at 20 mm.

Figure 7:

Blade profile of the vortex turbine (a) Side view (b) top view

Figure 8:

Different number of bladed turbines (b) five-bladed (c) six-bladed (d) eight-bladed (e) ten-bladed

3.3 Computational fluid dynamic Simulation

The ANSYS 17.2 package was used to solve the CFD simulations. The ANSYS ICEM software was used to create an unstructured hexagonal mesh for the fluid domains of the GWVP plant provided with the necessary refinements, as shown in Figure 9.

Figure 9:

(a) Hexagonal mesh of GWVP plant's fluid domains (b) Mesh on the turbine blade surface (c) Mesh refinement near blade wall and basin inner wall

Special attention was paid to the mesh refinement near the wall to capture the boundary layer effect and the free water-air interface to distinguish a clear interface. The O-grid concept was applied to mesh the turbine fluid to refine the mesh around the blade surfaces. The first layer thickness around the blade wall was 0.01 mm resulting in a maximum y⁺ of approximately 15 on the blade surface, indicating the reliability of the mesh around the blade. The total number of mesh elements was 2.25x10⁶ where 1.1x10⁶ was in the turbine domain.

CFD simulation was performed using the ANSYS CFX tool. Steady-state simulations were conducted for all cases that were solved using the Reynold Average Navier –Stokes (RANS) equations. Thus, a homogeneous multiphase model was introduced to define air and water. Gravity was defined as 9.81 m/s² and a density different buoyancy model and a free surface model were selected because the water and air can be separated, rather than having a mixture model. The surface tension coefficient was introduced as 0.072 N/m, indicating that water was the primary fluid. The reference pressure was set as the atmospheric pressure (1atm).

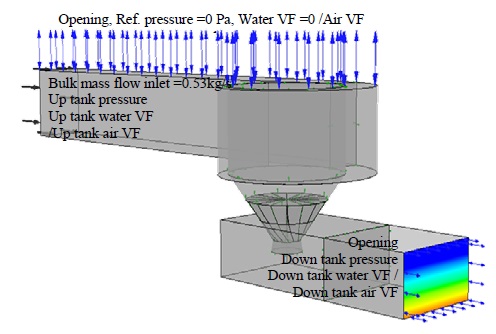
Only the turbine domain is defined as a rotational domain that rotates at a given rotational speed, whereas the rest of the domains are considered as stationary domains. The interface between the rotational and stationary domains is defined as the general grid interface (GGI) connection. The 530 kg/s bulk mass flow rate was defined as the inlet condition for the inflow channel, while the outlet was defined as having a constant water level given by the appropriate hydraulic pressure. The top surface of the basin was defined as an opening with the same atmospheric pressure. The basin walls, turbine blades, and shafts indicate a no-slip smooth wall.

In Figure 10, the boundary conditions for the CFD set-up are summarized. Based on the recommendations of several studies, the shear stress transport (SST) turbulence model was introduced with circular correction [10]. Thus, the SST model is highly recommended for turbomachinery simulations because it produces a more realistic solution. In solver control, the maximum iteration was set to 5000, and the residual target was fixed at 1 × 10⁵.

Figure 10:

Boundary conditions of CFD set up for GWVP plant simulation

The torque on the turbine blades was monitored during the process of solving the simulations.

4. Results

4.1 Validated study

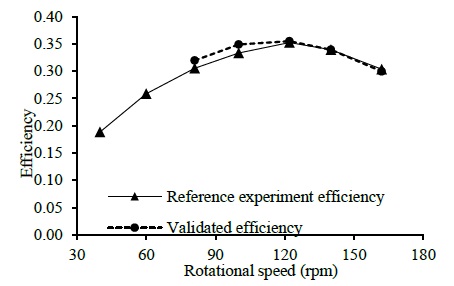
The experimental results of the Yasuyuki Nishi and Terumi Inagaki vortex turbines [2] were used to validate the ANSYS CFX setup. In this particular study, a turbine with twenty blades, was installed inside a cylindrical vortex basin. A maximum efficiency of 35 % was recorded in this configuration, and they compared the simulation and experimental performance, where the experimental results were used to validate the current CFD setup. The basic dimensions of the validated vortex turbine are listed in Table 1.

Table 1:

Basic dimensions of validated vortex turbine model

In Figure 11, the water flow behavior for the validated model is illustrated,whereas in Figure 12, a comparison of the efficiency of the validated CFD study with the experimental study is shown. The variations in the validated efficiency showed fair agreement with the experimental study, showing a slight deviation in the efficiency for only two rotational speeds. As the maximum deviation was below 5%, the overall results of the validation were recognized as suitable for simulating a new model of the GWVP plant.

Figure 11:

Simulated water flow behavior for validated model

Figure 12:

Validated efficiency comparison with reference experimental study

4.1 Performance of modified GWVP plant

The CFD simulations reached the steady state condition after 2000 iterations, despite being run further, up to 5000 iterations. The values of the residuals for the u, v, and w momentums converged to below 10-3 and the mass imbalance was less than 2%. The monitor point of the torque varied around a constant at a value of 0.4% bandwidth. The GWVP plant performance was measured using hydraulic efficiency, calculated using CFD simulations. The efficiency graphs were followed by variations in the torque and hydraulic head. The variations in the torque were considered to be related to the extracted power for a given rotational speed. The hydraulic head is related to the available power for a constant flow rate. The effect of the number of blades in the vortex turbine and the effect of the draft tube were observed for different rotational speeds, and the efficiency curves were constructed, as shown in Figures 13 and 14.

Figure 13:

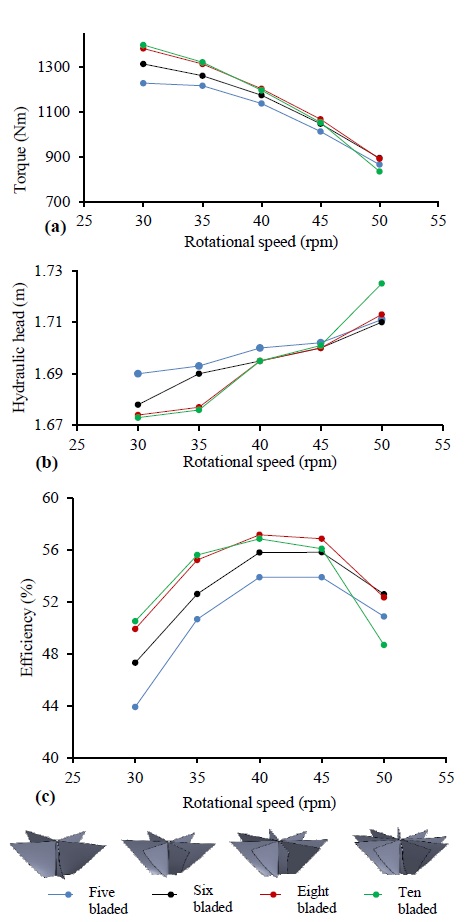
GWVP plant performance for turbine consist with different number of blades (a) Torque variation (b) Hydraulic head variation (c) CFD efficiency variation

Figure 14:

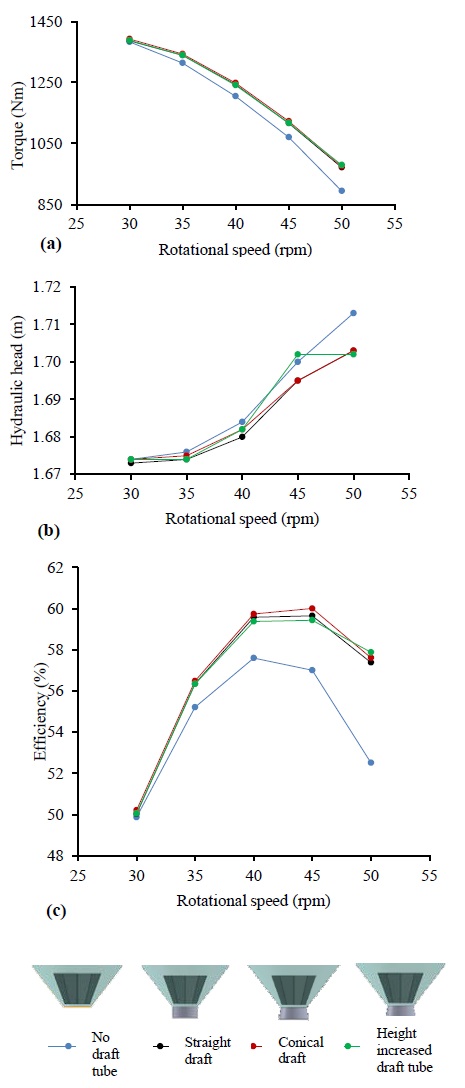
GWVP plant performance for different draft tube designs (a) Torque variation (b) Hydraulic head variation (c) CFD efficiency variation

In the first part of the research, an investigation was conducted on the effect of the number of blades in the vortex turbine. In Figure 13, variations in the torque and hydraulic head, as well as the CFD efficiency for different numbers of blades in the vortex turbine are illustrated. The initial turbine had five blades and it yielded 54% maximum efficiency, between 40-45 rpm. When the number of blades was increased from five to eight, the peak efficiency of the GWVP plant also increased, resulting in the highest efficiency of 57.2%. However, when the number of blades was increased from eight to ten no significant difference was observed, but there was a slight reduction at higher rotational speeds. The main reason for the increase in the efficiency of the turbines with a higher number of blades is the increase in the torque, accompanied by a slight decrease in the hydraulic head, as shown in Figure 10.

Figure 14 illustrates the variations in the torque and hydraulic head, as well as the CFD efficiency for different draft tube designs. The draft tube effect can be clearly observed, as it tends to increase the efficiency by approximately 3%. The effects of the straight and conical draft tubes remain almost unchanged following the common trend curve of performance. In addition, any increase in the height of the conical draft tube did not affect the performance. The addition of the draft tube to the vortex basin exerts its effect as it increases the torque of the turbine. This is because it helps to maintain the low-pressure region at the bottom-back side of the turbine blade, increasing the pressure drop across the blade. This phenomenon is explained in detail in the Discussion section.

5. Discussion

The performance of each of the simulated GWVP plant cases can be justified using flow analysis in the CFD post process. Three main parameters related to the flow were analyzed: water-air inter phase (at 0.5 water volume fraction), water superficial velocity, and pressure contours.

In the case of turbines with different numbers of blades, the performance was observed to increase when the number of blades was increased from five to eight. When the blade number was increased, the turbine exposed a large area to the vortex, extracting a relatively large quantity of energy. Therefore, the torque of the turbine increased at an optimal rotational speed between 40 and 45 rpm. On the other hand, no significant change in the performance was noted when the number of blades was increased to ten, even though the effective area of the turbine increased significantly. This is because the ten-blade turbines would block the water outflow while avoiding air core formation. In the presence of the vortex turbine, the air core is parted and propagated behind the turbine blade maintaining the low-pressure region, while discharging at the circumference of the drain outlet. Therefore, without the air core, the low-pressure region was not maintained, and hence, the pressure drop across the turbine blade was reduced. In Figure 15, the propagation of the air core behavior for turbines with different numbers of blades shows that turbines with fewer blades tend to maintain a larger air core, while a higher number of blades in the turbines produce only small air cores.

Figure 15:

Water and air behavior for different numbers of bladed turbine (water-air interface is defined by 0.5 water volume fraction) (a) five-bladed (b)six-bladed (c) eight-bladed (d) ten-bladed

The water superficial velocity vector fields, illustrated in Figure 16, show water circulation at the blade tip for fewer turbines (denoted by red circles in Figure 16). This is because a large water mass impacts on the turbine blade, resulting in splashing and circulation. In the case of turbines with a large number of blades, the water mass is divided among the blades and hence exerts less impact on a single blade, resulting in less splashing of water.

Figure 16:

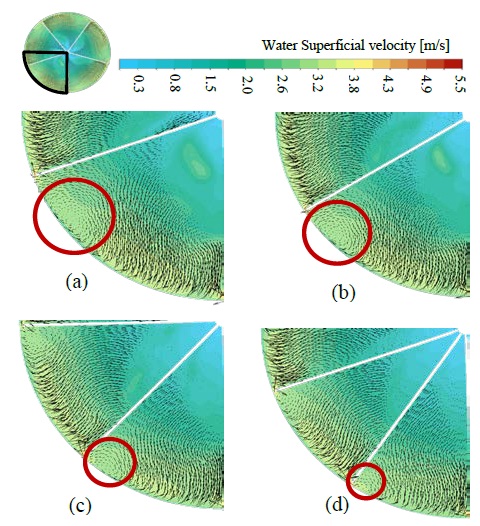
Water superficial velocity contour and velocity vector on quarter-horizontal cross section of the turbine (red circle area denotes the circulation) (a) five-bladed (b)six-bladed (c) eight-bladed (d) ten-bladed

Figure 17 illustrates the pressure contour on the turbine blades. The high-pressure region can be observed at the outer edge of the front surface of the blades, and the pressure decreases gradually toward the center axis. A back-pressure region was also visible at the upper tip area of the back surface of the blades. This back pressure continues to propagate when the number of blades is increased. Owing to the high blockage in the ten-blade turbines, water is entrapped in a smaller space between the two blades, while the rear blade pushes the entrapped water, thus generating the back pressure. Hence, the performance does not show significant improvement for the ten-blade turbine, although the hit has the highest area of exposure.

Figure 17:

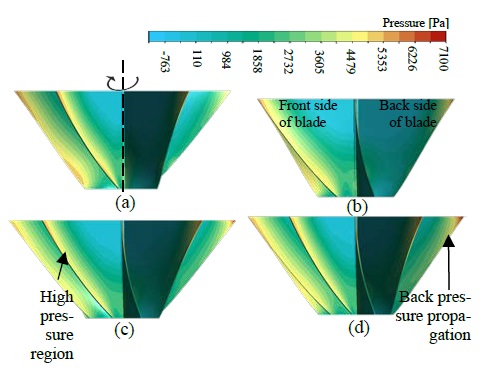
Pressure contour on blade surfaces for different number of bladed turbines (a) five-bladed (b)six-bladed (c) eight-bladed (d) ten-bladed

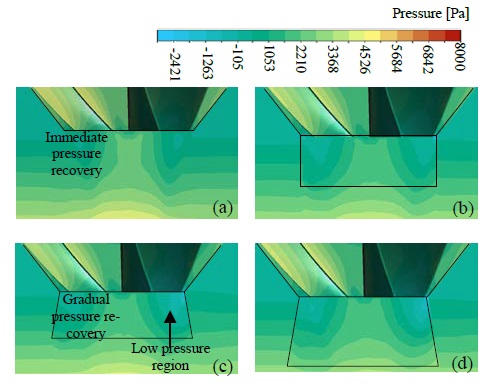
Modifying the vortex basin by adding a small draft tube increased the performance of the GWVP plant by approximately 3%. The main responsibility of the draft tube is to maintain a low-pressure region at the bottom of the basin, while it gradually recovers. In Figure 18, the pressure contour in the vertical plane around the draft tube is shown. In the case of no draft tube, the low-pressure region at the circumference of the drain outlet is recovered immediately by blocking the outlet using the down-channel water or air. Hence, the vortex air core propagation was reduced inside the basin, adversely affecting the performance. The addition of a small draft tube tends to recover the pressure gradually, maintaining the low-pressure region at the bottommost position of the basin, while allowing the vortex air core to discharge easily at the circumference of the drain outlet. On the other hand, the low-pressure region affects the turbine bottom by supporting the maintenance of a pressure drop across the blade, resulting in a higher torque than the no-draft tube case. The effects of the straight and conical draft tubes were similar, while the flow diverged via the conical draft tube. The height of the draft tube does not exert any significant effect on the performance because the low-pressure region generated in the GWVP plant is relatively low, and the pressure is very quickly recovered other than the Francis or Kaplan turbines.

Figure 18:

Pressure contour on vertical cross-section plane around draft tube (a) No draft tube (b)straight draft tube (c) conical draft tube (d) height increased draft tube

6. Conclusion

GWVP plant technology has gained popularity in recent times as a micro-hydropower extraction method. Therefore, much research continues, at present, involving the optimization of the gravitational water vortex power extraction method, while developing a standard design procedure. This study was conducted to observe the effect exerted by the number of blades in a verticalaxis vortex turbine and the effect of the draft tube in the vortex basin design. The study was based chiefly on CFD analysis, followed by a validation model. The initial GWVP plant design was performed for a selected installation site, adapting the recent research findings.

Using the same blade profile, the turbines were modeled each with 5,6,8 and ten blades. The eight-blade turbines showed good performance for the design, yielding a hydraulic efficiency of 57 %. Thus, for the eight-blade turbines, the exposure area to the vortex is optimal, while maintaining a stable air core propagation. Turbines with fewer blades caused water splash owing to the impact of a massive water mass on a single blade. Turbines with a greater number of blades tend to block water outflow, thus propagating back pressure. Modifying the vortex basin by adding a smaller draft tube enhanced the performance of the GWVP plant, raising the hydraulic efficiency up to 60%. The draft tube helps to recover the low-pressure region gradually from the drain outlet of the basin to the down channel.

The research is supposed to continue by simulating a wide range of flow rates. Hence, the effect of the number of blades in the turbine can be clarified further while observing the CFD flow field.

Acknowledgments

This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korean government (MOTIE) (20194210100170-Demonstration of development of renewable energy convergence system for fisheries).

References

• A. Kuriqi, A. N. Pinheiro, A. Sordo-Ward, M. D. Bejarano, and L. Garrote, “Ecological impacts of run-of-river hydropower plants- Current status and future prospects on the brink of energy transition,” Renewable and Sustainable Energy Reviews, vol. 142, 2021. [https://doi.org/10.1016/j.rser.2021.110833]
• Y. Nishi, and T. Inagaki, “Performance and flow field of a gravitation vortex type water turbine,” International Journal of Rotating Machinery, 2017. [https://doi.org/10.1155/2017/2610508]
• R. Dhakal, R. K. Chaulagain, T. Bajracharya, and S. Shrestha, “Economic feasibility study of gravitational water vortex power plant for the rural electrification of low head region of Nepal and its comparative study with other low head power plants,” ASIAN Community Knowledge Networks for the Economy, Society, Culture, and Environmental Stability conference, 2015. [https://doi.org/10.13140/RG.2.1.4383.4483]
• V. J. A. Guzmán, J. A. Glasscock, and F. Whitehouse, “Design and construction of an off-grid gravitational vortex hydropower plant: A case study in rural Peru,” Sustainable Energy Technologies and Assessments, vol. 35, pp. 131-138, 2019. [https://doi.org/10.1016/j.seta.2019.06.004]
• O. Alexandersson, “Living water -Viktor Schauberger and the secrets of natural energy,” 1982.
• A. Gautam, A. Sapkota, S. Neupane, J. Dhakal, A. Babu Timilsina, and S. Shakya, “Study on effect of adding booster runner in conical basin: Gravitational water vortex power plant: A numerical and experimental approach,” Proceedings of IOE Graduate Conference, 2016.
• S. Dhakal, A. B. Timilsina, R. Dhakal, D. Fuyal, T. R. Bajracharya, H. P. Pandit, N. Amatya, and A. M. Nakarmi, “Comparison of cylindrical and conical basins with optimum position of runner: Gravitational water vortex power plant,” Renewable and Sustainable Energy Reviews, 2015. [https://doi.org/10.1016/j.rser.2015.04.030]
• S. Dhaka, A. B. Timilsina, R. Dhakal, D. Fuyal, T. R. Bajracharya, H. P. Pandit, and N. Amatya, “Mathematical modeling, design optimization and experimental verification of conical basin: Gravitational water vortex power plant,” World’s Largest Hydro Conference, 2015. [https://doi.org/10.13140/RG.2.1.1762.0083]
• M. M. Rahman, T. J. Hong, and F. M. Tamiri, “Effects of inlet flow rate and Penstock’s geometry on the performance of gravitational water vortex power plan,” 2018.
• S. Mulligan, “Experimental and numerical analysis of three-dimensional free-surface turbulent vortex flows with strong circulation,” Ph. D. Dissertation, Institute of Technology, Sligo, 2015.
• I. -H. Choi, J. -W. Kim, and G. -S. Chung, “Experimental study of micro hydropower with vortex generation at lower head water,” Journal of Wetlands Research, vol. 22, no. 2, May 2020. [https://doi.org/10.17663/JWR.2020.22.2.121]
• J. A. Chattha, T. A. Cheema, and N. H. Khan, “Numerical investigation of basin geometries for vortex generation in a gravitational water vortex power plant,” The 8th International Renewable Energy Congress (IREC 2017), 2017.
• S. Dhakal, S. Nakarmi, P. Pun, A. B. Thapa, and T. R. Bajracharya, “Development and testing of runner and conical basin for gravitational water vortex power plant,” Journal of the Institute of Engineering, vol. 10, no. 1, 2014.
• A. S. Saleem, T. A. Cheema, R. Ullah, S. M. Ahmad, J. A. Chettha, B. Akbar, and C. W. Park, “Parametric study of single-stage gravitational water vortex turbine with cylindrical basin,” Energy, 2019. [https://doi.org/10.1016/j.energy.2020.117464]
• R. Dhakal, T. R. Bajracharya, S. R. Shakya, B. Kumal, S. J. Willianson, K. Khanal, S. Gautam, and D. P. Ghale, “Computational and experimental investigation of runner for gravitational water vortex power plant,” 6th International Conference on Renewable Energy Research and applications, San Diego, USA, 2017.
• T. R. Bajracharya, S. R. Shakya, A. B. Timilsina, J. Dhakal, S. Neupane, A. Gautam, and A. Sapkota, “Effects of geometrical parameters in gravitational water vortex turbines with conical basin,” Journal of Renewable Energy, 2020. [https://doi.org/10.1155/2020/5373784]
• M. M. Rahman, J. H. Tan, M. T. Fadzlita, and A. R. Wan Khairul Muzammil, “A review on the development of gravitational water vortex power plant as alternative renewable energy resources,” International Conference on Materials Technology and Energy, IOP Conference Series: Material Sicence and Engineering, 2017. [https://doi.org/10.1088/1757-899X/217/1/012007]
• C. Power, A. McNabola, and P. Coughlan, “A parametric experimental investigation of the operating conditions of gravitational vortex hydropower (GVHP),” Journal of Clean Energy Technologies, vol. 4, no. 2, 2016. [https://doi.org/10.7763/JOCET.2016.V4.263]
• B. N. Tran, B. -G. Kim, and J. -H. Kim, “The effect of the guide vane number and inclined angle on the performance improvement of a low head propeller turbine,” Journal of Advanced Marine Engineering and Technology, vol. 45, no. 4, 2021.
• L. Hai-feng, C. Hong-xun, M. Zheng, and Z. Yi, “Experimental and numerical investigation of free surface vortex,” Journal of Hydrodynamics, vol. 20, no. 4, 2008. [https://doi.org/10.1016/S1001-6058(08)60084-0]
• S. Mulligan, G. De Cesare, J. Casserly, and R. Sherlock, “Understanding turbulent free-surface vortex flows using a Taylor-Couette flow analogy,” Scientific reports, 2017.
• P. Sritram and R. Suntivarakorn, “The effects of blade number and turbine baffle plates on the efficiency of free-vortex water turbines,” IOP Conference Series: Earth and Environmental Science, 2019. [https://doi.org/10.1088/1755-1315/257/1/012040]