Performance analysis of machine learning for fault diagnosis of ballast water treatment system
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The demand for ecofriendly ships in shipbuilding and maritime industries is growing steadily. In response to strict environmental regulations on shipping by the International Maritime Organization, the demand for ship machinery and equipment that carry ecofriendly labels, including ballast water treatment systems (BWTS), is increasing. The BWTS involves early-stage equipment error and fault diagnostics, and its malfunction can have major cost and time consequences. This study expands on previous research on fault diagnosis using the SVM, a machine learning model. The two aspects of this expansion are an increased window size range used to generate the features and the introduction of several machine learning models. We used 47,435 sensor data points to compare and analyze the results and evaluate the classification accuracy by increasing the window size range to 10. We demonstrate that the previous model can be easily applied to other machine learning models and that the SVM model improves performance through feature generation. The F1 score of the random forest model with the highest performance score of 99.73% indicates potential for industrial applications if accompanied by expert monitoring and verification.
Keywords:
Ballast water treatment system, Fault diagnosis, Machine learning1. Introduction
Global attention to climate-related issues has increased to encompass environmental regulations, such as policies for reducing greenhouse gas emissions. In the shipbuilding and maritime industries, the demand for ecofriendly vessels is growing in response to strengthening environmental regulations for ships implemented by the International Maritime Organization. Ecofriendly vessels comply with emission regulations for carbon dioxide, nitrogen oxide, sulfur oxide, and ballast water [1]. Ecofriendly ship equipment refers to machinery or equipment installed on ships to satisfy these regulations.
A ballast water treatment system (BWTS) is an ecofriendly ship equipment that complies with ballast water discharge regulations. The ballast water of a ship is channeled into the cargo loading area to maintain balance based on the cargo loading conditions. The water is then discharged from the unloading areas at the destination port and is a major cause of marine ecosystem disruption. Strict regulations have been formulated to enforce appropriate ballast water treatment before discharge. Representative ballast water treatment techniques include ultraviolet (UV) irradiation, ozone spraying, chemical treatment, and electrolysis methods [2].
A BWTS malfunction may cause a vessel to be denied entry by the authorities at the destination port. Such malfunctions lead to cost- and time-related damages that are significantly greater than the BWTS repair costs. Alongside the growing importance of BWTS is a fast-emerging focus on fault diagnosis technology capable of identifying equipment failure or error [3]. General machine or equipment failure diagnosis techniques, including those for the BWTS, are classified into physical model-driven and data-driven diagnosis categories. The data-driven diagnosis techniques are further divided into signal and machine learning methods [4].
The signal-based diagnosis method uses a range of values for evaluating the normal state of a sensor. If the measured sensor value is outside the range, failure is considered to have occurred. In a previous study [5], a fault diagnosis of the BWTS was performed using this method. However, the limitation of the signal-based diagnosis method is that the scope of troubleshooting is restricted to one sensor. Conversely, in the machine learning-based method, the model can automatically learn the features related to the failure between the sensors using the acquired sensor data in the normal and failure states.
In this study, BWTS fault diagnosis was performed using machine learning based on data obtained from five types of UV lamp sensors. Such sensors are the core components of UV-projection BWTS equipment.
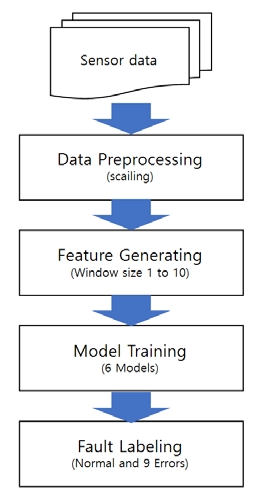
The proposed process involves four steps. The first step is data preprocessing, which entails converting BWTS sensor data from an operating vessel into floating-point numbers between zero and one. This process is essential and prevents overfitting during the learning process of the operation of a machine learning model, as there are significant differences between the minimum and maximum values calculated for each sensor [6]. The second step is feature generation, in which sequential data are converted into a window size. Generally, if a recurrent neural network (RNN) [7], a type of deep learning, is used in sequential data, all previous information at the time of learning is stored in hidden states. However, in this study, the current state of fault was diagnosed using only a limited amount of previous-stage data rather than a neural network that would require many resources for direct application in industrial settings. The third step is model training. In this study, six machine learning models were trained using BWTS sensor data. The fourth step is a fault-diagnosing step in which performance evaluation was conducted by applying six trained machine learning models to the evaluation data. This study expanded on a previous study [9] in which fault diagnosis was performed using a support vector machine (SVM) [8] to compare the ranges of feature generation and fault diagnosis accuracy corresponding to different machine learning models.
The remainder of this paper is organized as follows. Section 2 presents the sensor data fault diagnosis and machine learning models. Section 3 describes the BWTS fault diagnosis using sensor data and machine learning-based models. Section 4 describes the range of feature generation and evaluation of experiments using machine learning models. Section 5 presents conclusions drawn from the results and outlines recommendations for future studies.
2. Related Work
2.1 Fault diagnosis
Industrial facilities are connected to building systems, with some facilities having complex arrangements of various complex devices. If a device malfunctions, the performance of the entire system may be affected, and the system may undergo damage. Monitoring techniques for devices and facilities are continuously being developed to prevent such incidents. Such techniques utilize various types of sensors to diagnose faults and predict device lifespans. Such techniques are collectively referred to as prognostic and health management (PHM) [10].
The PHM technique consists of four components. The components are as follows: (1) data sensing, in which the characteristics of facilities are analyzed, and sensor systems are used to detect abnormal conditions; (2) preprocessing and feature generation, in which statistical and physical characteristics related to faults are generated from the data collected during data sensing; (3) diagnosis, in which normal and fault conditions are determined based on the features generated during preprocessing and feature generation; (4) prognosis, which involves predicting the lifespan of the system or equipment in terms of the time until the next fault occurs.
The data used in this study were collected from five types of sensors and measured in intervals of 1 s at the BWTS “GloEn-Patrol” facility manufactured by Panasia Co., Ltd using the UV projection method. Therefore, the data generation step of the PHM process was not required. Feature generation through window-size-driven transformation and diagnosis was performed using six machine learning models. Table 1 lists the five types of sensors used for data acquisition.
2.2 SVM
SVM is an algorithm that performs binary classification by determining the optimal linear decision boundary [8]. A decision boundary is a hyperplane with the maximum margin between the data labels. The maximum margin is the maximum Euclidean distance between the nearest data and the hyperplane discovered by the SVM. The hyperplane is expressed by Equation (1), where x is the x-axis value on the hyperplane, wT is the gradient of the decision boundary, and b is the maximum margin.
| (1) |
| (2) |
Binary classification is conducted to identify the maximum margin, and learning is performed to achieve the correct classification of new data (u1) based on the value of Equation (2), which multiplies the classification target of Equation (1).
Multiclassification is performed by one-versus-rest (OvR) for a decision boundary for each label type or by one-versus-one (OvO) for the binary classification decision boundary in all cases [11]. The most significant difference between OvR and OvO is the number of decision boundaries. Because the OvR method has only one decision boundary, one vector is classified into only one class in the vector space. The OvO method constructs decision boundaries corresponding to each pair of existing classes. Therefore, a vector can be divided into two or more classes according to the decision boundary. The final classification result of the OvO method is determined by the class most classified by all decision boundaries.
2.3 Logistic Regression
Logistic regression is a binary classification algorithm that outputs a probability between zero and one using a logistic equation and a latent variable [12]. Logistic regression differs from SVM primarily in that logistic regression explores decision boundaries using logistic equations. The hyperplane is determined using Equation (3), where is the input vector, Y denotes the classified class of , and is the gradient vector corresponding to the values inside .
| (3) |
Binary classification is performed based on if the right side of Equation (3) is less or greater than zero.
Multiclassification is performed by subtracting the probability that the data correspond to a specific label from 1 using the OvR method of SVM.
2.4 k-Nearest Neighbors (k-NN)
A k-NN algorithm is a machine learning algorithm that performs classification based on the Euclidean distance between each data point using a user-defined constant k [13]. Each labeled multidimensional characteristic space vector is used as the learning data element. The Euclidean distance for each data element is a k label based on the user-defined constant k.
2.5 Multilayer Perceptron
A perceptron is a basic neural network model whose workings are based on neuronal activities. It is an algorithm that produces an output from multiple inputs [14]. Each perceptron outputs a value of one if the weighted sum of the inputs exceeds a given threshold; otherwise, the output value is zero.
A multilayer perceptron is a structure with several layers stacked to ensure that the output of a perceptron is used as an input into another perceptron. When a multilayer perceptron is used in a multiclassification task, as many perceptrons as the number of labels in the last layer (zero and one are output according to each label) are arranged.
2.6 Random Forest
A random forest is an ensemble machine learning model based on a decision tree algorithm [15] that prevents the overfitting of decision tree tasks. It completes the process of bootstrap aggregation, in which the number of learning data elements for generating each decision tree and its features are selected as a subset of the total number.
decision tree algorithm proceeds with learning in the direction in which the information gain is maximized for each branch node. The information gain is determined using Equation (4), where S is the data set arriving at a node, Sf is the data set entering the left or right child node of the S node, and H(S) is the Shannon entropy of the S data set.
| (4) |
This value is obtained by subtracting the entropy value of the child nodes from the entropy value of the parent node. Maximizing information gain refers to learning in a direction that reduces the complexity of the classification result as the number of tree branches increases.
2.7 eXtream Gradient Boosting (XGBoost)
XGBoost is an ensemble machine learning model based on a boosting method, unlike the random forest algorithm, which is based on the bootstrap aggregation method. In contrast to bootstrap aggregation, boosting uses a decision tree as a weak classifier and reteaches the following decision tree by assigning weights to data elements that have failed to be classified precisely [16]. The objective function is expressed by Equation (5), and minimal learning should proceed.
| (5) |
In Equation (5), Ω is the weight function used for regularization to prevent overfitting, ut is the correct answer class of the input data, is the class predicted by the model, and the l function is the loss function for the difference between ut and .
3. BWTS Fault Diagnosis Using Machine Learning Models
In this paper, we present a fault diagnosis system using five types of sensor data extracted from the UV lamps of a BWTS. UV lamps are core components for achieving the function of a BWTS. Sensor data for the ballast water flow rate, pressure, and temperature were selected as training data to check the normal operation of UV lamps and a BWTS. The proposed system comprises four steps, as shown in Figure 1.
The first step is data preprocessing, in which the values of sensor data with different output values are converted into real numbers between zero and one. The second step is feature generation, in which the features necessary for machine learning are generated. The third step is training, in which machine learning models are established using the generated features. The fourth step is the diagnosis, in which the trained machine learning models are applied to the evaluation data.
3.1 Data preprocessing
The machine learning models used in this study were classified according to the algorithm formula of each model. However, if significant differences exist between the input feature values, classification performance may deteriorate, or overfitting may occur. For the sensor data, the range of values calculated for the sensors may vary significantly, depending on the fields or units measured using the sensors. Table 2 list an excerpt from typical sensor data.
The #S F_DP sensor had a value ranging between 0.12 and 0.26, but the #S FLOW sensor had a value ranging between 478.0 and 513.0 (Table 2). If the difference is used as learning data for the machine learning model without scaling, performance degradation or overfitting may occur.
Methods for adjusting the numerical ranges include standard scaling and minmax scaling [4]. In this study, the sensor data were scaled to floating-point numbers between zero and one using minmax scaling, as expressed by Equation (6).
| (6) |
In Equation (6), x is the raw data value measured by a sensor at a specific time, and xmax and xmin are the maximum and minimum values, respectively, measured by the sensor throughout the entire period.
3.2 Feature generation
Time-series data were collected repeatedly for a specific process over a particular period. A typical deep learning model that uses time-series data is the RNN, which uses all data input before each learning step. A feature is generated to predict the current situation using a number n of previous observations, considering the specificity of the industrial sites. This approach is in contrast to neural network-driven models that require extensive learning resources.
Suppose a row of sensor data is x. All the acquired time-series sensor data can be represented by (x1, x2, …, xn). Because of the characteristics of time-series data, using only one row x for learning may adversely affect the performance of machine learning models. Therefore, in this study, the data for the stage belonging to a window were generated as new features while moving the window, whose size was fixed at values ranging from 1 to 10. Window refers to the continuous number of x to be used as the input data. For example, if the window size was set to 2, features were generated in the form of [(x1, x2), (x2, x3), …, (xn-2, xn-1), (xn-1, xn)], and if the window size was expanded to 3, the features were generated in the form of [(x1, x2, x3), (x2, x3, x4), …, (xn-2, xn-1, xn)].
In this feature-generation method, an effective window size analysis is necessary for each machine learning model. As the window size increases, the time-series data characteristics improve, and the data size used by the machine learning models also increases. Therefore, the classification accuracy is evaluated according to the window size.
3.3 Model training
Unlike in previous studies in which fault diagnosis was performed using SVM only, five additional machine learning models were used in this study. Table 3 lists the machine learning models used for fault diagnosis.
The BWTS fault diagnosis task is converted into a multi-classification process that produces 11 labels as outputs, that is, the normal state and 10 fault states for five types of sensor data from the machine learning models. Scikit-learn [17], a module of the Python programming language, was used to implement, learn, and evaluate each model, and default values were borrowed for all model parameters.
SVM and LR models use the OvO (R) method to perform multiclassification. OvO (R) is a method that splits multiple classifications into all available binary classifications. A k-NN model borrows labels for the k-nearest data by measuring the Euclidean distance between each learning data element. Classification is preceded by designating the largest number of labels as the labels for the step data. Perceptron produces binary outputs, such as SVM and LR models. Therefore, MLP sets the number of perceptrons in the last layer equal to the number of labels to perform multiclassification tasks. Each perceptron is allocated to a label and learns as many binary classifications as the number of labels. The RF model performs ensemble learning using the bootstrap aggregation method on multiple decision trees. Each decision tree is trained by dividing the learning data and features into multiple subsets. The XGBoost model is an ensemble model that uses a boosting method on multiple decision trees. Unlike bootstrap aggregation, which teaches multiple decision trees at once, the boosting method trains only one decision tree at a time, weighing nodes of the tree that fails classification and then trains the next decision tree. Therefore, a single strong classifier is generated by the multiple decision trees of an ensemble, which performs the role of weak classifiers.
4. Experiment and Evaluation
4.1 Experimental setup
The BWTS sensor data are crucial for learning and evaluating machine learning models. Figure 2 shows the UV unit of the “GloEn-Patrol” BWTS facility of Panasia Co., Ltd., which provided the sensor data used in this study.
Out of the 47,430 sensor data elements acquired, 45,911 were normal data, and 1,519 were fault data. These data reflect an imbalance, that is, a very low proportion of fault data to normal data. Thus, the proportions of the normal and fault data in the learning and evaluation data sets were set differently for each label to reduce the imbalance and improve the suitability of the evaluation results for the machine learning models. In the training step, the number of normal data was increased to be as similar as possible to the actual installation site of the BWTS. In addition, the ratio of the fault data was higher than that of the normal data in the evaluation step to determine whether the trained model performed fault diagnosis correctly. The statistics of the data division for each label are listed in Table 5.
We used the Python programming language for feature generation and machine-learning model learning. For feature generation for window sizes of 1–10, Numpy [18] and Pandas [19]modules were used. The Scikit-learn module was used to implement and test each machine learning model. All model parameters borrowed default values, except for “OvO” in SVM and LR.
4.2 Feature generation performance by window size
The sensor data used for learning and evaluation were time-series data observations obtained in intervals of 1 s. To evaluate the suitability based on the window size during feature generation, we measured the accuracy of the machine learning models with window sizes ranging from 1 to 10. Table 6 presents the classification accuracy results based on the window size for the six models.
The accuracy of the SVM model tended to decrease with increasing window size. This is the OvO method, which performs binary classification between label pairs. It appeared that an increase in the number of dimensions of support vectors generated a hyperplane that increased the classification complexity. In contrast, the accuracy of the LR model tended to with an increase in the window size. This trend occurred owing to the OvR method used by the LR model in performing multiple classifications. Unlike the OvO method, which carries out multiple classifications by performing binary classification between label pairs for all cases, the OvR method performs multiple classifications by removing the probability of the remaining labels from the total probability. Therefore, it appeared that the transfer of more features improved the accuracy of the probability calculations for the hyperplane determination of the LR model.
The k-NN, MLP, RF, and XGBoost models showed improved accuracy up to specific window size, after which the accuracy remained similar to that for a window size of 1. Although the effects were weaker than those of the SVM and LR models, the classification accuracy tended to increase as the window size was increased to reflect the time-series data. Furthermore, the RF model demonstrated the highest accuracy. This result could be attributed to unbalanced learning progression of the bootstrap aggregation ensemble method, despite the minimal amount of fault data.
The conclusive differences compared to the results of previous studies are encouraging. Unlike previous studies that demonstrated fault diagnosis using only the SVM model, the results of this study show that feature generation according to window size is valid for other machine learning models. By comparing window sizes ranging from 1 to 5, we confirm that a window size of 2 is suitable for the SVM model. However, by comparing window sizes ranging from 1 to 10, we demonstrate that the feature generation method is unsuitable for the SVM model.
4.3 Performance analysis of RF model
We evaluated the performance of the RF model using a window size of six, which yielded the highest accuracy. The evaluation showed improved accuracy under all conditions compared to those of previous studies. Table 7 lists the confusion matrix for the experimental results of the RF model. Table 8 presents the six evaluation measures [20] obtained using the values listed in Table 7.
A true positive is a frequency at which a steady state is predicted accurately, whereas a false positive is a frequency at which a fault is predicted as normal. A false negative is the frequency of a fault being predicted, even in a normal state, whereas a true negative is the frequency of a fault being predicted accurately. The positive predictive value is called precision in the same term, and it refers to the ratio of correct predictions among the model predicted to the normal state. The true positive rate is called recall in the same term and refers to the ratio of correct predictions among actual normal state data.
Precision is a score indicating the prediction accuracy of the state of a BWTS. The RF model exhibited the best performance, as indicated by a precision value of 100%. The recall rate, which is a measure of the accuracy of the predicted fault state, was 99.46%. This value indicated that approximately 0.5% of the faults were undetected. The F1 score of 99.73% was the harmonic mean of precision and recall. The false alarm rate is defined as the rate at which the normal state is incorrectly predicted as a fault. The false alarm rate of the RF model was 0%, indicating the case in which the normal state was classified as a fault. Specificity, the rate at which the fault state is predicted to have a fault, was determined by subtracting the false alarm rate from 1, recorded as 100%. In summary, the false alarm rate and specificity, including precision and recall, reflected excellent performance. We believe that this model is appropriate for application in the industrial sector. However, further confirmation and monitoring by experts are essential, as some areas need to be further evaluated to implement complete unmanned systems.
5. Conclusion
In this study, we expanded on previous studies by conducting feature generation based on window sizes of time-series data and performing fault diagnosis of BWTS sensor data using six machine learning models. By expanding on the experiments conducted in previous studies, we confirmed that the classification performance of several types of machine learning models according to window sizes could be improved, but we observed that this did not apply to the SVM model. We demonstrated that the k-NN, MLP, RF, and XGBoost models outperformed the SVM in multiclassification tasks.
The F1 score of the RF model showed the highest classification accuracy (99.73%). These experimental results are reasonably expected at industrial sites using expert monitoring and verification systems. However, further research is needed to resolve imbalances between normal and fault data, such as those noted in this paper.
Acknowledgments
This paper is based on research conducted by the Ministry of Trade, Industry and Energy in 2019 with the support of the Korea Industrial Complex Corporation project to enhance the competitiveness of industrial clusters. And this Work was partially supported by the Ministry of Education of the Republic of Korea and The National Research Foundation of Korea (NRF-2019M3E8A1103533).
Author Contributions
Conceptualization, H. M. Park, S. G. Cheon, J. H. Kim, and S. D. Lee; Methodology, H. M. Park, J. H. Kim, and S. D. Lee; Hardware and Data Generation; S. G. Cheon, and S. D. Lee; Software, H. M. Park, J. H. Kim; Validation, H. M. Park, J. H. Kim, and S. D. Lee; Data Management, H. M. Park, and S. G. Cheon; Writing-Original Draft Preparation, H. M. Park;Writing-Review & Editing, H. M. Park, S. G. Cheon, J. H. Kim, and S. D. Lee.
References
- International Maritime Organization, https://www.imo.org/en/OurWork/Environment/Pages/BallastWaterManagement.aspx, , Accessed March 21, 2021.
-
E. C. Kim, “Consideration on the ballast water treatment system technology and its development strategies,” Journal of the Korean Society for Marine Environmental Engineering, vol. 15, no. 4, pp. 349-356, 2012 (in Korean).
[https://doi.org/10.7846/JKOSMEE.2012.15.4.349]

-
S. H. Sohn, Y. -C. Kim, and K. K. Choi, “Numerical study on fluid characteristics due to disc shape in a novel mechanical ballast water treatment system,” Journal of the Korean Society of Marine Engineering, vol. 39, no. 1, pp. 19-27, 2015.
[https://doi.org/10.5916/jkosme.2015.39.1.19]

-
A. Mouzakitis, “Classification of fault diagnosis methods for control systems,” Measurement and Control, vol. 46, no. 10, pp. 303-308, 2013.
[https://doi.org/10.1177/0020294013510471]

-
J. -N. Seo, S. -J. Kim, H. -S. Kwon, and J. -M. Kim, “Failure prediction of BWTS and failure repair using e-Navigation,” The Journal of the Institute of Internet, Broadcasting and Communication, vol. 17, no. 1, pp. 145-151, 2017.
[https://doi.org/10.7236/JIIBC.2017.17.1.145]

- A. Géron, Hands-On Machine Learning with Scikit-Learn, Keras and Tensorflow: Concepts, Tools, and Techniques to Build Intelligence Systems, 2nd edition, O’Relliy, 2019.
-
D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning representations by back-propagating errors,” Nature, vol. 323, pp. 533-536, 1986.
[https://doi.org/10.1038/323533a0]

-
C. Cortes and V. N. Vapnik, “Support-vector networks,” Machine Learning, vol. 20, no. 3, pp. 273-297, 1995.
[https://doi.org/10.1007/BF00994018]

- J. K. Kim, J. H. Kim, and S. D. Lee, “Diagnosing faults in BWTS based on machine learning”, International Journal of Computer Science and Network Security, vol. 20, no. 8, pp. 104-111, 2020.
- B. D. Yoon, T. W. Hwang, S. H. Cho, D. G. Lee, and G. M. Nah, “Diagnosis and prognostic of engineering system status using artificial intelligence”, Journal of the Korean Society of Mechanical Engineers, vol. 57, no. 3, pp. 38-41, 2017.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006.
-
D. R. Cox, “The regression analysis of binary sequences,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 20, no. 2, pp. 215-232, 1958.
[https://doi.org/10.1111/j.2517-6161.1958.tb00292.x]

-
N. S. Altman, “An introduction to kernel and nearest neighbor nonparametric regression,” The American Statistician, vol. 46, no. 3, pp. 175-185, 1992.
[https://doi.org/10.1080/00031305.1992.10475879]

-
F. Rosenblatt, “The perceptron: A probabilistic model for information storage and organization in the brain,” Psychological Review, vol. 65, no. 6, pp. 386-408, 1958.
[https://doi.org/10.1037/h0042519]

-
L. Breiman, “Random forests,” Machine Learning, vol. 45, pp. 5-32, 2001.
[https://doi.org/10.1023/A:1010933404324]

- C. Tianqi and C. Guestrin, “XGBoost: A scalable tree boosting system,” Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785-794, 2016.
- Scikit-learn: machine learning in Python & mdash; scikit-learn 0.24.2 documentation, https://scikit-learn.org, , Accessed April 25, 2021.
- NumPy, https://numpy.org, , Accessed April 25, 2021.
- Pandas - Python Data Analysis Library, https://pandas.pydata.org, , Accessed April 25, 2021.
-
H. M. Park, G. S. Park, Y. R. Kim, J. K. Kim, J. H. Kim, and S. D. Lee, “Deep learning-based drone detection with SWIR cameras”, Journal of Korean Society of Marine Engineering, vol. 44, no. 6, pp. 500-506, 2020.
[https://doi.org/10.5916/jamet.2020.44.6.500]