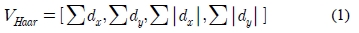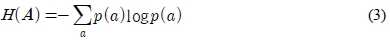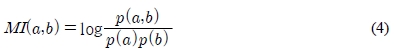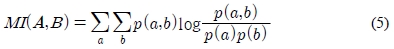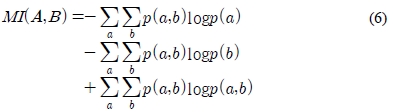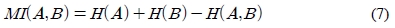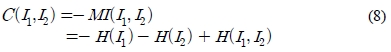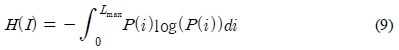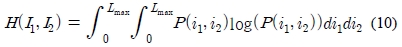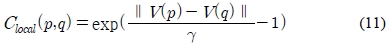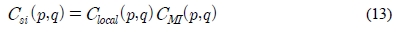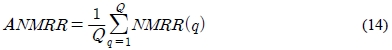A study on a local descriptor and entropy-based similarity measure for object recognition system being robust to local illumination change

1. 서 론

정보화 및 자동화 시대를 맞아 영상을 이용한 자동 인식 시스템에 대한 요구가 사회 각 분야에서 나날이 증가하고 있다. 이에 조선해양 및 항만물류 분야에서도 시대에 발맞춰 주어진 영상을 분석하여 컨테이너 차량 번호판을 자동으로 인식하거나 선박의 각 장소를 무인으로 감시하기 위한 컴퓨터 시각(computer vision) 기술의 필요를 느끼고 있으며 관련 연구가 진행 중이다. 컴퓨터 시각은 카메라로 얻은 한 장면을 분석하여 물체를 인식하거나 더 나아가 장면을 이해하기 위한 기술을 연구하는 분야이다. 이 중 물체 인식(object recognition) 및 영상 검색(image retrieval)을 위해 영상의 명암도나 칼라와 같은 저레벨(low-level) 요소들을 이용해 모양이나 내용을 표현하는 서술자(descriptor)와 이렇게 표현된 물체나 영상의 영역의 유사도를 정확히 판별하기 위한 연구가 활발히 진행 중이다[1]-[3].

지역 서술자(local descriptor)는 지역적인 서술에 기반하고 있다는 특성 때문에 시점의 변화가 발생한 영상 또는 가려짐이 발생한 영상에서도 정합을 가능케 한다. 대표적인 지역 서술자에는 GLOH (Gradient Location and Orientation Histogram)[4], SIFT (Scale-Invariant Feature Transform) [5], SURF (Speed-Up Robust Feature) [6], DAISY [7] 등이 있다. 이들의 공통점은 DoG (Difference of Gaussian) 필터와 같은 필터를 이용하여 키포인트를 찾고 그 점을 중심으로 일정한 영역 전체나 일정한 거리에 떨어진 화소들의 정보를 이용하여 고차원 벡터를 생성하는 과정을 거친다. 이러한 지역 서술자를 이용해서 표현된 영역이나 특징점은 크기변화 등 기하학적인 영상의 변환에 매우 강인한 성능을 보이지만 동일한 장면에서 조명의 차이가 발생한 경우 정합 성능이 저하되는 문제점이 있다[8]-[10].

최근 영상의 특징 서술, 영상 검색 및 스테레오 정합에 엔트로피를 적용하여 유사도를 계산하는 사례가 늘어나고 있다[9]-[11]. 엔트로피는 영상의 명암도 또는 색의 분포에 대한 결합확률을 이용한다. 이러한 특성으로 인해 전역적인 밝기 변화가 발생했을 때 대응점들의 유사도를 반영하는데 좋은 성능을 보이지만 서술 영역의 통계적인 특성만을 활용하기 때문에 질감이 적은 영역에 대한 유사도 반영에 문제가 생긴다.

본 논문에서는 지역적인 조명의 변화가 발생한 두 영상의 특징을 정확히 표현하기 위해 밝기 변화에 강인한 지역 서술자와 유사도 척도를 제안한다. 기존 지역 서술자들이 극복하지 못하는 밝기 변화에도 강인한 성능을 보이기 위해 제안한 방법은 특징점 주변의 주파수 특성을 표현할 수 있는 Haar 웨이블렛 필터 응답을 이용한 지역 서술자를 제안하고, 유사도 계산 과정에서 조명의 영향을 반영할 수 있도록 기존의 엔트로피 유사도와 지역 서술자의 차를 결합한 형태의 유사도 척도를 제안한다.

2. 제안한 지역 서술자

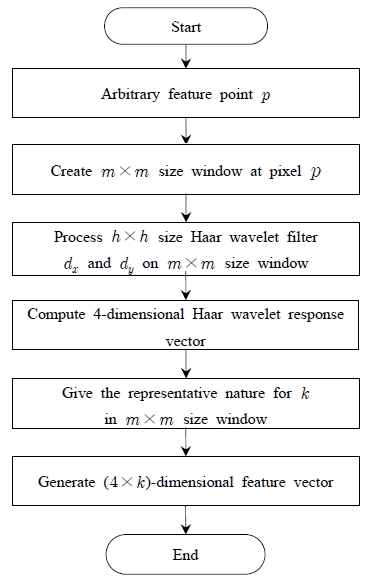
제안한 지역 서술자는 Haar 웨이블렛 필터의 응답으로 얻어진 특징 벡터들로 구성된다. 특징점을 중심으로 정해진 크기의 윈도우 영역에 대해 Haar 웨이블렛 필터를 통과시켜 4차원의 Haar 웨이블렛 응답 벡터를 얻고 특징점 주변의 화소에 대해 대표성을 부여하여 정의된 크기의 특징 벡터를 얻을 수 있다. Haar 웨이블렛 특징 벡터를 얻는 과정은 Figure 1과 같다. 특징 벡터를 얻기 위해 현재 화소 p를 중심으로 m×m크기의 윈도우를 형성한다. 여기에 h×h 크기의 Haar 웨이블렛 필터를 통과시켜 m×m 윈도우의 각 화소에 대해 4차원 Haar 웨이블렛 응답을 얻는다. m×m 영역에 대한 대표성을 부여한다. 이 때 대표성을 부여하는 화소의 갯수 k개에 대해 전체 벡터의 크기는 4×k개로 얻을 수 있다.

Figure 1:

A flowgraph of Haar wavelet feature vector at arbitrary feature point p

2.1 Haar 웨이블렛 응답 벡터

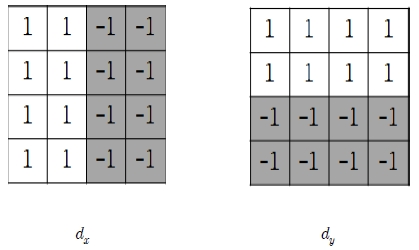
Haar 웨이블렛 응답 영상을 얻는데 사용하는 4×4 크기의 근사화된 Haar 웨이블렛 필터의 예는 Figure 2와 같다. x방향의 응답을 얻기 위해 d_x를 사용하고, y방향의 응답을 얻기 위해 d_y를 사용한다. d_x를 통해 얻는 응답 ∑d_x는 x방향으로 변하는 명암도 변화량의 총합으로, 정해진 영역의 x방향에 대한 명암도의 증가 혹은 감소의 정도를 의미한다. ∑ |d_x|는 x방향으로 명암도 변화의 발생 여부를 표현하며 고주파 성분이 포함되면 큰 값을 갖는다. y방향에 대한 d_y의 응답 또한 동일한 특성을 갖는다. 이런 과정을 거쳐 식 (1)과 같은 4차원의 Haar 웨이블렛 응답 벡터 V_Haar를 얻는다.

Figure 2:

Template Approximated Haar wavalet filter (x direction and y direction)

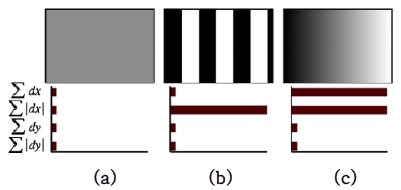
Haar 웨이블렛 응답 벡터는 식 (1)의 4개의 성분으로 특징점 지역의 화소값 분포에 대한 주파수의 방향과 특성을 표현할 수 있다. 화소값 분포별 Haar 웨이블렛 응답의 예는 Figure 3과 같다. 영역 전반적으로 동일한 화소값이 분포된 Figure 3 (a)의 경우 특징 벡터의 성분 4개의 크기가 작다. 화소값이 가로방향으로 구형파 형태로 나타나는 Figure 3 (b)의 경우 절대값 성분이 최대치를 갖고 나머지 성분은 0에 가깝다. 마지막으로 화소값이 단조증가 형태로 변하는 Figure 3 (c)와 같은 경우 화소값이 변하는 방향의 성분 두개는 최대값을 갖고 나머지 값은 0이다. Haar 웨이블렛 응답은 지역의 명암도가 어느 방향으로 어떻게 변하는지 주파수 개념으로 서술할 수 있는 장점을 지니고 있다. 그리고 Haar 웨이블렛 응답은 실제 조명치의 추정 오차에 불변한 성질을 갖는다. 대비의 변화에 대해 불변한 특성을 지니고 있기 때문에 영상의 이득(gain) 변화에 강인하다.

Figure 3:

Properties of Haar wavelet response about 3 intensity patterns (a) homogeneous (b) presense of frequencies in x direction (c) monotonic increasing in x direction

2.2 지역 서술자

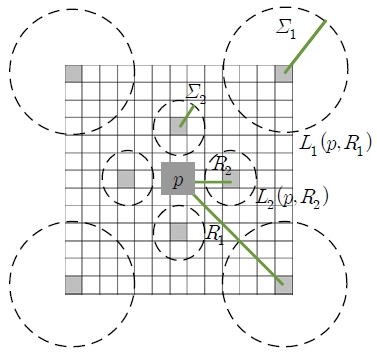
제안한 지역 서술자는 앞 절에서 설명한 4차원 벡터를 특징점 뿐만 아니라 특징점 주변의 화소들에게 대해 계산하여 얻어진 4차원 벡터들에 대해 대표성을 부여하여 특징 벡터의 변별력을 높일 수 있다. 예를 들어 화소 p를 중심으로 하는 13×13 크기의 윈도우 영역에 대해 대표성을 부여하는 예는 Figure 4와 같다. 이 때 p를 중심으로 반경 R₂는 7이 된다. 윈도우 영역의 정해진 위치에서 가중합을 구하여 특징 벡터를 구성할 수 있다. 이와 같은 경우 특징 벡터의 크기는 대표성을 띄는 9개의 화소가 4차원의 응답 벡터를 가지므로 36차원이 된다.

Figure 4:

Proposed local feature vector

Figure 5:

A flowgraph of computing proposed similarity measure

3. 지역 서술자와 엔트로피 기반 유사도 척도

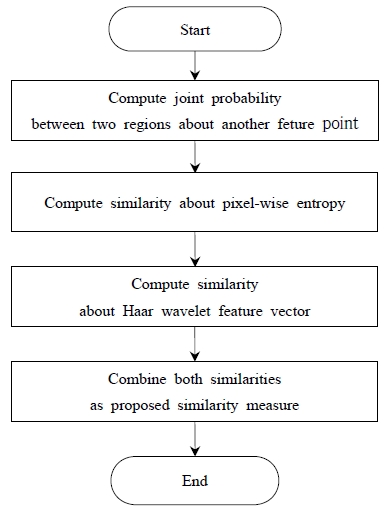
제안한 방법의 유사도 척도는 앞절에서 설명한 Haar 웨이블렛 특징 벡터를 이용해 얻은 지역 서술자와 엔트로피로 구성된다. 엔트로피 유사도는 지역 서술자를 얻을 때 정의된 특징점 주변의 영역에 대한 확률 분포를 이용하여 계산한다. 제안한 유사도 척도를 계산하는 과정은 Figure 5과 같다.

3.1 특징점 중심 영역의 상호정보 유사도 척도

어떤 사건 a의 발생확률이 p(a)일 때 해당 사건의 정보량(information content)은 식 (2)와 같다[12].

이산확률변수 A의 각 사건에 대한 정보량을 발생확률에 따라 가중 평균한 것을 평균정보량(average information content) 또는 엔트로피(entropy)라고 하며 식 (3)와 같다.

정보량의 경우 두 사건 a와 b가 동시에 발생할 확률과 독립적으로 발생할 확률의 비율을 상호정보량(mutual information)이라고 하며 식 (4)와 같다

여기서 p(a,b)는 사건 a와 b에 대한 결합확률이다.

엔트로피에 대한 상호정보량은 식 (4)의 정보량에 대한 상호정보량을 동시발생 사건의 확률을 곱한 평균값으로, 평균 상호정보량이라고 한다. 평균 상호정보량은 식 (5)와 같다.

평균 상호정보량은 log 연산을 합으로 풀면 식 (6)과 같다.

식 (6)의 우변의 항들은 식 (3)을 이용해 엔트로피로 나타낼 수 있다. 각 항을 순서대로 엔트로피로 나타내면 식 (7)과 같다.

여기서 H(A)와 H(B)는 각각 확률변수 A와 B에 대한 엔트로피이고, H(A,B)는 각각의 확률변수에 대한 엔트로피이다.

영상의 두 영역 I₁과 I₂에 대한 평균 상호정보량은 두 영역의 유사도를 측정할 수 있는 척도로 사용할 수 있다. 두 영역의 비용함수 C(I₁, I₂)를 정의하여 유사도 척도로 간주할 수 있다. 즉 비용함수가 클수록 유사성이 없다고 볼 수 있다. 따라서 비용함수 C(I₁, I₂)는 식 (8)과 같이 두 영역의 상호정보량 MI(I₁, I₂)을 반전시킨 것으로 정의할 수 있다.

화소값 범위 [0, L_MAX]에 대한 자기 엔트로피는 식 (9)와 같다.

여기서 P(i)는 영역 I에 포함된 화소값 i를 갖는 화소의 비율을 의미한다.

이와 같은 방법으로 상호 엔트로피는 식 (10)를 통해 계산할 수 있다.

여기서 P(i₁, i₂)는 영역 I₁에 포함된 화소값 i₁과 영역 I₂에 포함된 화소값 i₂의 결합확률이다.

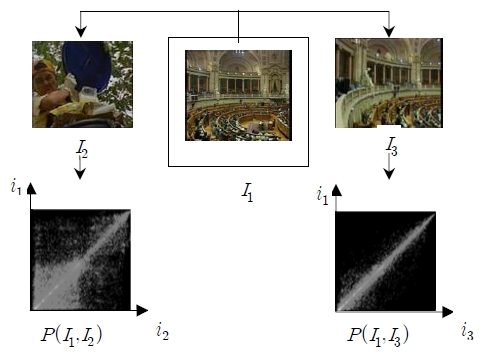
영상의 유사도에 따른 결합확률분포의 예는 Figure 6와 같다. 기준 영상 I₁과 비교적 유사도가 높은 I₃에 대한 결합확률분포는 대각선 방향으로 분포가 집중되어 있는 것을 확인할 수 있다. 그리고 I₃에 비해 유사도가 낮은 영상 I₂에 대한 결합확률분포가 대각선 방향을 중심으로 넓게 분포되어 있다. 이 때 상호 엔트로피는 큰 값으로 계산된다.

Figure 6:

Jonit probability distribution of two different images corresponding to reference image I1

특징점을 중심으로 하는 영역의 엔트로피를 계산한 후 지역 서술자를 구성하는 주변 화소를 중심으로 하는 영역의 엔트로피도 계산해야 한다. 이 때 모든 화소에 대한 엔트로피를 계속적으로 계산하는 것은 효율성이 떨어지므로 제안한 방법은 Talyor 급수 전개와 Parzen 추정 기법을 이용하여 화소 단위로 엔트로피를 추정하는 방법을 사용하였다[11].

4. 실험 및 고찰

제안한 방법의 성능을 검증하기 위해 두 종류의 실험을 실시하였다. 첫 번째 실험에서는 다양한 조명 변화에 대한 성능을 보이기 위해 같은 장면에서 전역적인 밝기 변화가 발생한 영상과 지역적인 밝기 변화가 발생한 영상 전체에 대한 유사도를 구하여 다른 방법들과 비교하였다. 정합여부는 동일한 위치의 화소에서 계산된 유사도의 비율이 0.6이내인 경우 정합된다고 판단하였다.

두 번째 실험은 1355개짜리 영상 검색 데이터베이스에 제안한 방법을 적용하여 기준 영상과 유사한 결과 5개를 제시하도록 하여 다른 방법들과 비교하였다. 검색 성능을 판별하기 위해 ANMRR [13]을 계산하여 제시하였다. ANMRR은 식 (14)와 같다.

여기서 Q는 전체 영상의 수이고 q는 대상 영상의 순번이다. NMRR은 기준 영상(query image)와 대상 영상 q와의 유사도를 0~1로 나타낸 것이다. ANMRR은 검색 성능이 우수할수록 작게 계산된다.

4.1 밝기 변화가 발생한 영상의 정합

전역적으로 밝기 변화가 발생한 영상에 대한 실험에는 동일한 장면을 카메라 조리개 노출 시간을 달리하여 얻은 영상들을 사용하였고 3개의 장면에 대해 각각 밝기가 다른 영상 3장을 사용하였다. 실험에 사용한 영상의 예는 Figure 7과 같다. e1은 저대비에 아주 어두운 영상이고 e3는 과도한 광량을 부여하여 촬영하였다.

Figure 7:

An example of test image set A (global illumination change)

제안한 방법과 다른 방법의 오정합 화소 비율은 Table 1과 같다.

Table 1:

Result about global illumination change test

CCH와 ART는 엔트로피 기반의 방법보다 오정합 화소 비율이 높음을 알 수 있다. CCH는 영상 전체의 칼라 정보만 사용하기 때문에 공간 정보 서술이 불가능하고 실험 영상과 같이 조명의 차이가 심할 경우 두 장면의 칼라가 변하기 때문에 서술자가 그 차이를 반영하지 못한다. ART는 HSI를 기반으로 서술자를 생성하기 때문에 RGB 기반인 CCH보다 밝기 변화에 강인한 성능을 보였지만 상대적으로 오정합 비율이 높다. 엔트로피를 사용한 방법은 알려진 바와 같이 전역적인 밝기 변화를 잘 반영함을 알 수 있다. 제안한 방법이 기존 엔트로피를 사용한 방법보다 성능이 좋은 이유는 지역 서술자를 이용한 공간 정보를 유사도 척도에 포함시켰기 때문이다.

지역적 밝기 변화가 발생한 영상에 대한 실험에 사용된 영상의 예는 Figure 8과 같다. 카메라 노출 시간을 일정하게 두고 조명의 방향과 색을 바꿔가며 촬영하여 조명의 차이가 지역적으로 다르게 발생한 영상을 사용하였다. 제안한 방법과 다른 방법의 오정합 화소 비율은 Table 2와 같다.

Figure 8:

An example of test image set A (local illumination change)

Table 2:

Result about local illumination change test

지역적인 조명의 변화가 발생하면 그림자의 방향과 조명광 자체의 색차가 발생하기 때문에 명암도와 칼라를 기반으로 하는 서술자의 성능이 저하된다. 이는 CCH의 오정합 비율이 높다는 사실을 통해 알 수 있다. 주목할 부분은 앞 실험에서 좋은 성능을 보였던 엔트로피를 이용한 방법의 성능 저하가 확연히 보인다는 점이다. 이는 지역적인 조명 변화 발생시 결합확률분포가 비선형 형태로 나타나기 때문에 같은 특징점에서도 엔트로피가 높게 계산되기 때문이다. 제안한 방법과 엔트로피의 오정합 화소 비율의 차이가 더 명확해졌다. 이는 불균일한 조명 조건에서 지역 서술자를 이용한 공간 정보가 유사도 반영에 도움이 된다는 사실을 말해준다. 제안한 방법의 지역 서술자는 Haar 웨이블렛 필터 응답을 이용하여 지역적 주파수 특성을 반영하므로 이러한 외란의 영향에 강인하다.

4.2 영상 검색 실험

실험에 사용한 기준 영상은 Figure 9와 같다. 전체적으로 질감이 고르게 분포되어 있는 것을 알 수 있다.

Figure 9:

An example of query image

Table 3:

Result about local illumination change test

기준 영상에 대한 각 방법의 5순위 결과 영상과 ANMRR 계산치는 다음과 같다.

CCH는 칼라의 분포적 특성만 분석하여 유사도를 판별하기 때문에 질감 정보를 반영하기 어렵다. ART는 CCH에 비해 질감을 묘사하는 성능이 비교적 좋지만 칼라의 분포 특성을 더 반영하는 특성이 있기 때문에 4순위로 제시한 영상을 기준 영상과 유사하다고 판별하였다. 제안한 방법으로 얻은 상위 5순위 영상들이 기준 영상과 매우 유사하며 ANMRR치도 기존의 방법들보다 적다. 이는 제안한 방법이 지역적으로 질감의 특성을 잘 반영한다는 사실을 보여준다.

5. 결 론

본 논문에서는 지역적인 조명의 변화가 발생한 두 영상의 특징을 정확히 표현하기 위해 밝기 변화에 강인한 지역 서술자와 유사도 척도를 제안하였다. 제안한 방법은 Haar 웨이블렛 필터 응답을 이용하여 특징점과 그 주변의 화소들의 특징 벡터를 연결하여 다차원 벡터의 형태로 지역 서술자를 발생시켰다. Haar 웨이블렛 필터 응답은 특징점을 포함한 영역의 주파수 특성을 반영하기 때문에 기존의 지역 서술자들이 놓치기 쉬운 질감 여부를 잘 반영하였으며 지역적인 밝기 변화에 대해 좋은 성능을 보였다. 그리고 제안한 유사도 척도는 기존의 엔트로피 기반의 유사도 척도에 제안한 지역 서술자의 차를 반영하여 결합한 형태이다. 이는 결합확률분포를 이용하여 전역적 밝기 변화에 강인한 엔트로피에 공간 정보를 반영할 수 있기 때문에 기존의 엔트로피가 지역적인 밝기 변화를 반영하지 못하는 문제를 해결할 수 있었다.

제안한 방법의 성능을 검증하기 위해 두 종류의 실험을 실시하였다. 먼저 밝기 변화가 발생한 영상에 대한 정합 성능을 보이기 위해 전역적인 밝기 변화와 지역적인 밝기 변화가 발생한 영상에 대해 각각 적용하였다. 제안한 방법이 우수한 성능을 보였으며, 특히 지역적인 밝기 변화가 발생했을 경우 제안한 지역 서술자 요소로 인해 탁월한 정합 성능을 보임을 확인할 수 있었다. 두 번째 영상 검색 실험에서도 제안한 방법의 성능이 우수함을 확인할 수 있었다. 향후 영상의 기하학적 변환을 반영할 수 있는 방향으로 연구가 필요하다.

References

• X. Han, Y. Chen, and X. Ruan, “Multilinear supervised neighborhood embedding of a local descriptor tensor for scene/object recognition”, IEEE Transactions on Image Processing, 21(3), p1314-1326, (2012).
• T. Engin, L. Vincent, and F. Pascal, “A fast local descriptor for dense matching”, IEEE Conference on Computer Vision and Pattern Recognition, p1-8, (2008).
• M. Krystian, and S. Cordelia, “A performance evaluation of local descriptors”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10), p1615-1630, (2005).
• K. Mikolajczyk, and C. Schmid, “A performance evaluation of local descriptors”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10), p1615-1630, (2005). [https://doi.org/10.1109/TPAMI.2005.188]
• D. G. Lowe, “Distinctive image features from scale invariant keypoints”, International Journal of Computer Vision, 20(2), p91-110, (2004).
• S. P. Nasholm, R. Hansen, S. E. Johansec, and B. Angelsen, “Transmit beams adapted to reverberation noise suppession using dual-frequency SURF imaging”, IEEE Transactions on Ultrasonics, Ferroelectircs, and Frequency Control, 56(10), p2124-2133, (2009). [https://doi.org/10.1109/TUFFC.2009.1295]
• T. Engin, L. Vincent, and F. Pascal, “DAISY:An efficient dense descriptor applied to wide-baseline stereo”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(5), p815-830, (2010).
• Y. Heo, K. Lee, and S. Lee, “Illumination and camera invariant stereo matching”, IEEE Conference on Computer Vision and Pattern Recognition, p1-8, (2008).
• U. Raghavendra, “Entropy based Log chromaticity projection for real-time stereo matching”, 2nd International Conference on Communication, Computing and amp; Security, 6, p223-230, (2012). [https://doi.org/10.1016/j.protcy.2012.10.027]
• P. Viola, and W. Wells, “Alignment by maximization of mutual information”, IEEE Proceeding in Sixth IEEE Inteligent Conference of Computer Vision, 24(2), p137-154, (1997).
• J. Kim, V. Kolmogorov, and R. Zabih, “Visual correspondence using energy minimization and mutual information”, IEEE Proceeding in Intelligent Conference of Computer Vision, 2, p1033-1040, (2003).
• M. Thomas, A. Thomas, and T. M. Cover, Elements of Information Theory, John Wiley & Sons, (2005).
• G. Ling, and C. Wang, “An image registration algorithm based on SIFT and CCH”, 2010 2nd International Conference on Computer Engineering and Technology, 7, p463-467, (2010).
• M. Turan, and H. K. Ekenel, “Shape-based facial expression classification using angular radial transform”, 2013 21st Signal Processing and Communications Applications Conference, p1-4, (2013). [https://doi.org/10.1109/SIU.2013.6531564]