Validation of methods for estimation of the heat flux into the liquid nitrogen pool from the concrete ground
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The vaporization velocity is one of the most important concepts in the study of the spread and vaporization of a flammable liquid pool because the pool spread and the pool vaporization interact with each other, and the vaporization velocity is the link. The numerical modeling of the vaporization velocity is determined by the heat flux into the liquid pool from the ground, and the heat flux can be determined by three models: the Inverse Heat Conduction Method (IHCM), the Boiling Regime Correlations (BRCs), and the assumption of Perfect Thermal Contact between the liquid and the ground surface (PTC). However, these methods have not been thoroughly validated against experimental results and compared with each other. In this work, the methods mentioned were validated against experimental results for a non-spreading pool on concrete ground, including the temperature inside the ground and the surface heat flux. It was found that (і) the IHCM can give a reliable prediction if the input and the time step are properly chosen, and (ii) the estimated heat flux based on the PTC generally agreed well with the experimental results, while that based on BRCs underestimated the results. This study might be beneficial for the development of spreading and vaporization models.
Keywords:
Pool spread, Vaporization, Inverse heat conduction method, Boiling correlation, Perfect thermal contact1. Introduction
The spread and vaporization of a flammable cryogenic liquid due to its accidental release on solid ground may result in a pool fire, an explosion, or a hazardous vapor cloud. The study of the spread and vaporization of cryogenic liquid pools is an important part of the risk assessment of cryogenic liquid storage facilities. The spreading pool is more probable than the non-spreading pool when a cryogenic liquid is released due to an accident. The pool spread and the pool vaporization are the major characteristics of the spreading pool. They closely interact with each other, with the vaporization velocity being the link. Numerical models that can predict the vaporization velocity of the spreading pool have been based on the non-spreading pool. The models are composed of the one-dimensional unsteady heat conduction equation with some conditions. The purpose of the modeling is to find the heat energy transferred into the liquid pool from the ground, which is the major heat source for pool vaporization.
It is known that at cryogenic temperature, the sensitivity of heat flux sensors significantly decreases. Therefore, it is impossible to use heat flux sensors to measure directly the heat flux at the ground surface. Instead, the surface heat flux and surface temperature can be obtained based on the measured temperature history inside the ground by using the Inverse Heat Conduction Method (IHCM) [1][2]. The IHCM is a popular method to estimate the surface heat flux or temperature when direct measurements are not possible. Several works [3]-[7] used the IHCM to calculate the heat energy transferred into a liquid nitrogen pool from solid substrates. However, the solutions were not compared with the experimental results.
In numerical models, Boiling Regime Correlations (BRCs) and the assumption of Perfect Thermal Contact (PTC) have been widely used as the boundary conditions at the ground surface to determine the surface heat flux. The BRCs were analytically derived for nucleate boiling [8] and film boiling [9]-[11]. The BRCs provide the relationship between the heat flux into the liquid pool and the temperature difference between the liquid and the ground surface. The correlations could be considered as the boundary condition in the heat conduction problem to obtain the transient surface heat flux [12][13]. However, the PTC has been commonly used in spreading models [13]-[17]. The PTC indicates that the surface temperature of the ground is kept constant at the boiling temperature of the liquid. Then, the surface heat flux can be obtained. Nguyen et al. [12] compared the predictions obtained from BRCs and PTC with experimental results for a spreading pool. However, the results were significantly influenced by the uncertainty of the pool radius measurements. A comparison among the heat fluxes with time into a non-spreading pool estimated by BRCs, PTC, and experimental results may be beneficial for the evaluation of the two methods. However, such a comparison has not been available so far.
In the authors’ previous work [18], the vaporization of a non-spreading liquid nitrogen pool was experimentally investigated. The aim of this work is to validate the methods for calculating the heat flux into the liquid pool from the ground, including IHCM, BRCs, and PTC, against the experimental results obtained from the previous work. The heat flux model in the non-spreading pool can be integrated to obtain the overall heat flux into the spreading pool. This study might be beneficial for the development of spreading and vaporization models.
2. Several Methods to Estimate the Heat Flux
2.1 Inverse heat conduction method
A direct heat conduction problem is to find the temperature distribution in a heat-conducting body with a known surface heat flux or surface temperature. In contrast, the determination of the surface heat flux or surface temperature based on transient temperature measurements at inner locations is an inverse heat conduction problem. The solution of the inverse heat conduction problem can be understood based on the solution procedure of a direct heat conduction problem as follows [1].
The temperature in a semi-infinite body satisfies the following equations:
| (1) |
| (1a) |
| (1b) |
| (1c) |
Here, T is temperature, t is time, z is the coordinate for depth in the ground, α and k are the thermal diffusivity and conductivity of the ground, Ta is the initial temperature of the ground, and q(t) is the heat flux.
The problem can be solved by using Duhamel’s theorem as follows [19]:
| (2) |
Here, ϕ is the solution of the same problem except for the unit surface heat flux q(t)=1.
| (3) |
The numerical approximation of Duhamel’s theorem is as follows:
| (4) |
The temperature vector is related to the surface heat flux vector as follows:
| (5) |
Here, Z is the sensitivity matrix, is the surface heat flux vector, and is the temperature vector.
As shown in Equation (5), the surface heat flux can be obtained by solving the system of linear equations with the given temperature history and the initial condition. The solution can be obtained by using the conjugate gradient method [2].
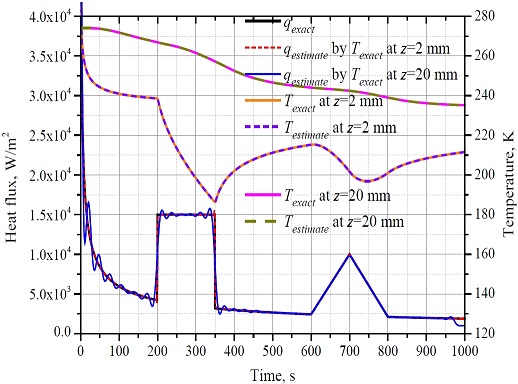
The verification of the IHCM is shown in Figure 1. The boundary condition for the direct heat conduction problem, qexact, was given. Solutions of the direct problem Texact at z=2 mm and z=20 mm were obtained. Then, the temperature histories Texact were used as inputs for the IHCM. The estimated temperatures Testimate and surface heat flux qestimate were then obtained using the IHCM. It can be seen that the estimated and exact temperatures agreed very well with each other for both cases. However, only the estimated heat flux based on the temperature at z=2 mm agreed well with the exact heat flux. The estimated heat flux curve based on the temperature history at z=20 mm remarkably deviated from the exact curve. This is due to the ill-posed characteristics of the inverse heat conduction problem caused by damping and lagging effects. The longer the distance from the measured point to the surface, the stronger the damping and lagging effects [1].
2.2 Assumption of perfect thermal contact
According to the PTC, the ground surface temperature is kept constant at the boiling temperature of the liquid. The surface heat flux is given by Equation (6) for the semi-infinite ground with the assumption of one-dimensional heat conduction [20].
| (6) |
2.3 Boiling regime correlations
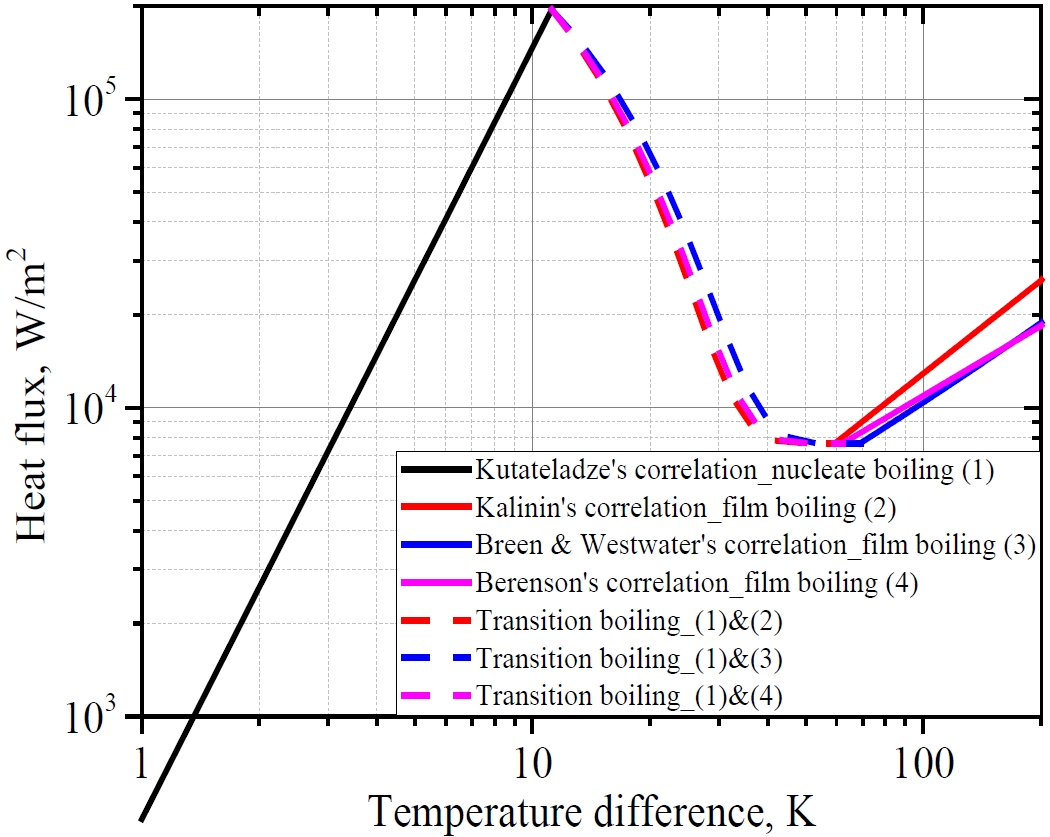
The correlations for the film boiling were given by Kalinin et al. [9], Breen and Westwater [11], and Berenson [10]. The correlation for nucleate boiling was proposed by Kutateladze [8]. The heat flux in the transition boiling was calculated by interpolation [9]. The correlations are shown in Table 1 and Figure 2. The correlations were theoretically derived. The good agreement between the correlations and experimental data for the steady boiling of liquid nitrogen at atmospheric pressure with the range of temperature difference from 1 to 200 K can be found in the report by Brentari et al. [21]. In the steady boiling test, the surface temperature was controlled. In transient boiling, as in this work, the ground surface was cooled naturally from its initial temperature to the cryogenic temperature.
3. Experimental Setup
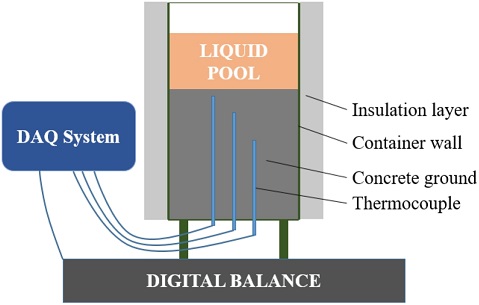
The purpose of this work was to measure both the temperature histories inside the concrete ground and the pool mass with time. The experimental apparatus included a container, cylindrical concrete ground, a digital balance, eight thermocouples, and a data acquisition system, as shown in Figure 3.
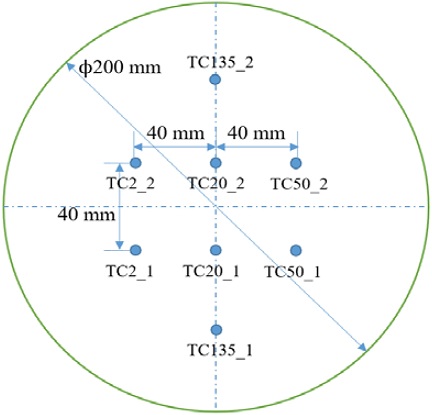
Liquid nitrogen was used in this study. The properties of nitrogen at atmospheric pressure were obtained from the U.S. National Institute of Standards and Technology (NIST) computer program known as REFPROP, as shown in Table 2. The dimensions and thermal properties of the cylindrical concrete ground are listed in Table 3. Before the experiments, the ground temperature was equal to the ambient temperature at 274 K. The thickness of the concrete ground was large enough that the ground could be regarded as a semi-infinite body. Eight thermocouples were installed in the concrete ground to record the temperature histories. Two thermocouples were located at the same depth (Thermocouples TC2_1 and TC2_2 at z=2 mm, TC20_1 and TC20_2 at z=20 mm, TC50_1 and TC50_2 at z=50 mm, and TC135_1 and TC135_2 at z=135 mm). The arrangement of the thermocouples can be seen in Figure 4. The temperature at depth z=135 mm was unchanged during the experiment, which confirmed the assumption of semi-infinite ground. The probe diameter and the response time of the thermocouples were 0.5 mm and 0.25 s, respectively. The sampling rate of the temperature was 100 Hz. The digital balance measured the pool mass with time. The data acquisition system recorded the signals from the thermocouples and the balance. A detailed description of the experimental apparatus can be found in the authors’ previous work [18].
Liquid nitrogen was stored at atmospheric pressure. The liquid was poured into the experimental apparatus while it was boiling. The data were recorded when the pouring process started. The pouring time was approximately 14 s.
In the experiments, the heat flux was estimated using Equation (7). Here, the heat conducted from the container wall into the liquid pool was negligible. It is worth noting that the heat flux obtained from the experiment is the average heat flux into the liquid pool from the entire ground surface.
| (7) |
Here, is the mass-loss rate of the liquid pool, Δm is the vaporized mass during the period of time Δt, λ is the latent heat of vaporization, and R is the radius of the cylindrical ground.
The expanded uncertainty for the heat flux was obtained by using the Taylor series method for the propagation of uncertainty as follows:
| (8) |
Here, Uq is the expanded standard uncertainty for the heat flux, and uΔm and uΔt are the combined standard uncertainty of Δm and Δt, respectively.
4. Results and Discussion
The pool mass data are shown in Figure 5. The pool mass sharply increased from zero to the maximum value during the pouring of liquid nitrogen into the container. After the pouring process stopped, the pool mass decreased owing to vaporization.
The heat flux obtained from an experimental run is shown in Figure 6. The maximum relative uncertainty of the heat flux was less than 15%.
In the initial period, the liquid pool boiled violently owing to the large temperature difference between the ground surface and the liquid. From t=0 to t=50 s, the heat flux into the liquid pool tended to decrease with time. A vapor film, which completely prevented the liquid pool from having direct contact with the entire ground surface, was not formed. However, a local vapor film was formed in some local areas. From t=50 to t=80 s, the heat flux slightly increased owing to the collapse of the local vapor film. In the remaining time, the heat flux decreased continuously. A detailed interpretation of the experimental results can be found in the authors’ previous work [18].
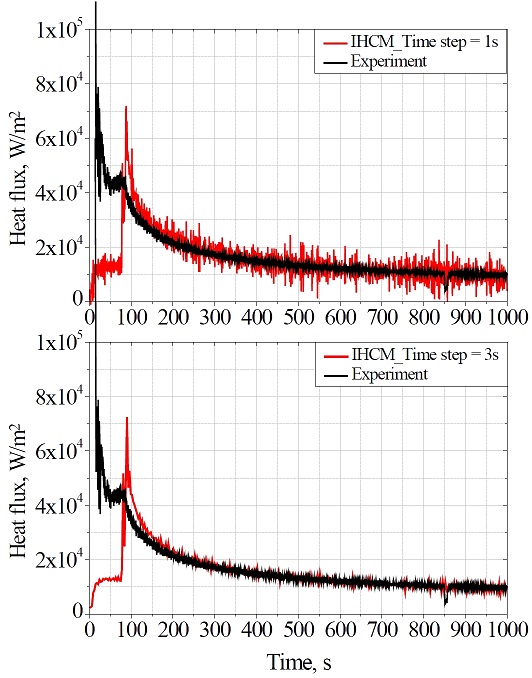
The experimental heat flux was used to validate the estimated heat flux obtained from the IHCM using the temperature histories measured at z=2 mm. Because the IHCM is extremely sensitive to measurement errors, the use of small time steps may cause instabilities in the solution. Therefore, the time step should be sufficiently large to obtain a better solution. As shown in Figure 6, two time step values were used to estimate the heat flux, i.e., Δt=1 and Δt=3 s. The larger time step resulted in a less deviated solution from the experimental results. It should be noted that the heat flux curve obtained from the IHCM was the local heat flux, which may be different from the average heat flux obtained from the experiment. The heat flux curve in the case of Δt=3 s can be divided into three segments along the experimental time. The first section is from t=0 to t=85 s, where the solution of the IHCM was lower than the experimental heat flux. This underestimation could be explained by the existence of a local vapor film. Hence, the local heat flux was limited and smaller than the average heat flux. The second section is from t=85 to t=150 s, where the solution of the IHCM surpassed the experimental heat flux owing to the collapse of the local vapor film. In the remaining time, the IHCM and experimental curves overlap well. The IHCM would have predicted the experimental heat flux better if the boiling regime of the liquid pool had been homogeneous over the entire ground surface.
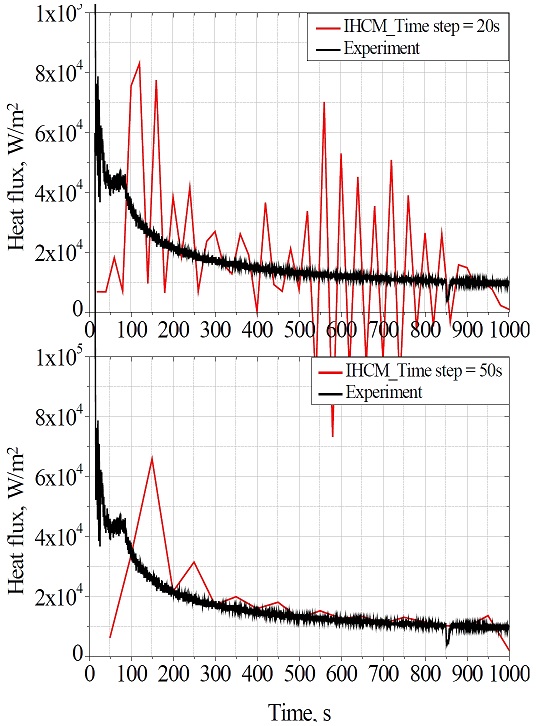
In addition, an attempt was made to investigate how the selection of the input influences the reliability of the IHCM’s prediction. To this end, the surface heat flux was additionally estimated by the IHCM using the measured temperature history at a deeper location, z=20 mm, as the input. As can be seen in Figure 7, the larger the time step, the better the estimation. A large time step, Δt=50 s, was required to obtain a rough estimation. This time step is much larger than that used in Figure 6, where the temperature of a point near the surface was used as the input for the IHCM. Because of the damping and lagging effects in heat conduction problems, the longer the distance from the measurement point to the surface, the more sensitive the IHCM is to the measurement errors. As a result, a larger time step is required. However, choosing a large time step reduces the amount of information obtained. Therefore, the input of the IHCM should be taken near the surface to obtain a more reliable estimation of the surface heat flux.
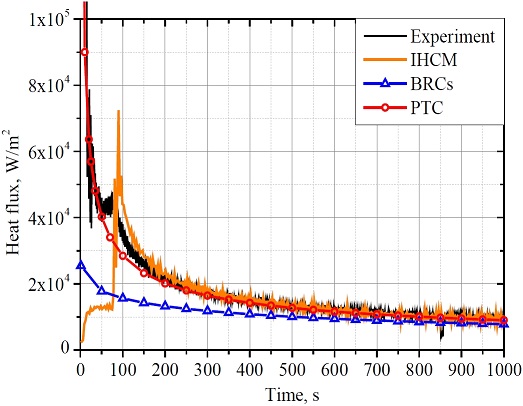
The heat fluxes estimated by IHCM (z=2 mm, Δt=3 s), BRCs, and PTC were compared with each other and with the experimental results. The correlations given by Kalinin and Kutateladze were used to draw the BRCs curve shown in Figure 8. Although Kalinin’s correlation predicted the highest heat flux among the three correlations for film boiling, the BRCs curve was lower than the experimental curve, especially in the initial period. The BRCs predicted that the liquid pool was in the film boiling during the entire experimental time. In contrast, the PTC curve agreed relatively well with the experimental results, except for the period from t=50 to t=150 s, where the collapse of the local vapor film occurred. After t=150 s, the IHCM, PTC, and experimental curves agreed well. In general, the PTC provided a better estimation of the heat flux compared with the BRCs in this work, where the conducting body was concrete with low thermal conductivity.
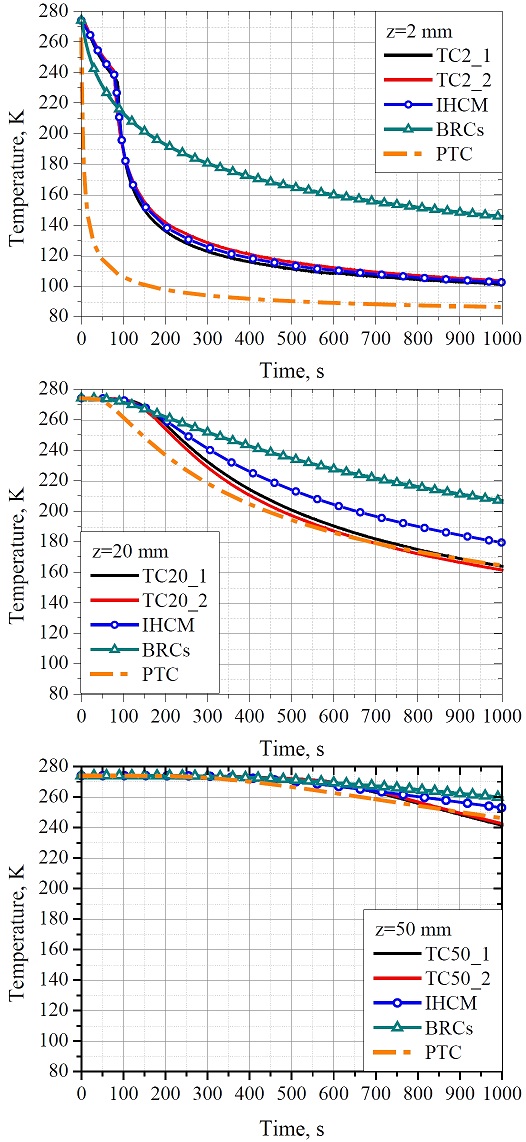
The temperatures predicted by IHCM, BRCs, and PTC were validated against experimental measurements at different depths, as shown in Figure 9. Because the measurements near the ground surface (z=2 mm) were used as the input for the IHCM, the curve estimated by the IHCM at z=2 mm agreed well with the experimental curves. However, remarkable deviations between predictions and measurements occurred at deeper locations. It is worth noting that the change in temperature at a location inside the concrete was mainly dependent on the local heat flux on the surface. Therefore, the deviations might be caused by nonhomogeneous boiling. Because the BRCs underestimated the surface heat flux, the predictions given by the BRCs overestimated the temperatures in the ground. The PTC underestimated the temperature during the entire experimental period at z=2 mm. This is because the PTC overestimated the heat flux in the initial time. As the PTC accurately predicted the heat flux after t=150 s, the difference between the PTC temperature curves and the experimental results reduced with time at deeper locations.
5. Conclusions
In this work, several methods used to estimate the heat flux into a liquid pool from concrete ground, including the IHCM, BRCs, and PTC, were validated against experimental results.
The IHCM utilizes the measured temperature inside the ground to calculate the surface heat flux. Because of the ill-posed characteristics, the time step must be large enough to avoid instabilities in the solution of the IHCM. It was experimentally confirmed that the distance between the measured location and the ground surface should be as short as possible to obtain a detailed and reliable estimation. Since the IHCM estimated the local heat flux, the estimated curve deviated from the experimental results because of the nonhomogeneous boiling in the initial period. When nucleate boiling occurred, the solution of the IHCM agreed well with the experimental results. It is believed that the IHCM can be an effective method for estimating the surface heat flux.
The PTC and BRCs have been used in numerical models as boundary conditions at the ground surface. As validated against experimental results, the BRCs underestimated the heat energy transferred into the liquid pool. Generally, the PTC can provide a better prediction compared with the BRCs for the vaporization of a cryogenic liquid on concrete ground.
Nomenclature
| Cp : | specific heat |
| g : | gravitational acceleration |
| k : | thermal conductivity |
| N : | number of time steps |
| : | mass-loss rate of the liquid pool due to the heat from the ground |
| Δm : | vaporized liquid mass |
| P : | pressure of the liquid |
| q : | heat flux |
| R : | radius of the cylindrical ground |
| T : | temperature |
| ΔT : | temperature difference between the liquid and the ground surface |
| t : | time |
| U : | expanded standard uncertainty |
| u : | combined standard uncertainty |
| Z : | sensitivity matrix |
| z : | coordinate for depth in the ground |
Greek symbols
| α : | thermal diffusivity |
| λ : | latent heat of vaporization |
| μ : | dynamic viscosity |
| ν : | kinematic viscosity |
| ρ : | density |
| σ : | surface tension of the liquid |
Subscripts
| a : | ambient |
| b : | boiling |
| f : | film |
| l : | liquid |
| n : | nucleate |
| v : | vapor |
| t : | transition |
| CHF : | critical heat flux |
| MHF : | minimum heat flux |
Acknowledgments
This research was supported by the Research Program funded by the Ministry of Oceans and Fisheries of Korea (Grant number: MF0590).
Author Contributions
Conceptualization, K. Chung and M. Kim; Methodology, K. Chung, Y. Han, and L. -D. Nguyen; Formal Analysis, K. Chung and M. Kim; Investigation, K. Chung and M. Kim; Resources, K. Chung; Data Curation, K. Chung; Writing—Original Draft Preparation, K. Chung; Writing—Review & Editing, M. Kim, Y. Han, and L. -D. Nguyen; Supervision, M. Kim; Project Administration, K. Chung; Funding Acquisition, K. Chung.
References
- J. V. Beck, B. Blackwell, and C. R. St. Clair Jr., Inverse Heat Conduction: Ill-Posed Problems, 1st Edition: Wiley-Interscience, 1985.
-
J. V. Beck and K. A. Woodbury, “Inverse heat conduction problem: Sensitivity coefficient insights, filter coefficients, and intrinsic verification,” International Journal of Heat and Mass Transfer, vol. 97, pp. 578-588, 2016.
[https://doi.org/10.1016/j.ijheatmasstransfer.2016.02.034]

-
R. Li, Z. Huang, G. Li, X. Wu, and P. Yan, “Study of the conductive heat flux from concrete to liquid nitrogen by solving an inverse heat conduction problem,” Journal of Loss Prevention in the Process Industries, vol. 48, pp. 48-54, 2017.
[https://doi.org/10.1016/j.jlp.2017.04.001]

-
R. Li, Z. Huang, X. Wu, P. Yan, and X. Dai, “Cryogenic quenching of rock using liquid nitrogen as a coolant: Investigation of surface effects,” International Journal of Heat and Mass Transfer, vol. 119, pp. 446-459, 2018.
[https://doi.org/10.1016/j.ijheatmasstransfer.2017.11.123]

-
R. Li, X. Wu, and Z. Huang, “Jet impingement boiling heat transfer from rock to liquid nitrogen during cryogenic quenching,” Experimental Thermal and Fluid Science, vol. 106, pp. 255-264, 2019.
[https://doi.org/10.1016/j.expthermflusci.2019.04.016]

-
R. Li, C. Zhang, and Z. Huang, “Quenching and rewetting of rock in liquid nitrogen: Characterizing heat transfer and surface effects,” International Journal of Thermal Sciences, vol. 148, 2020.
[https://doi.org/10.1016/j.ijthermalsci.2019.106161]

-
X. Shao, L. Pu, X. Tang, S. Yang, G. Lei, and Y. Li, “Experimental study of transient liquid nitrogen jet impingement boiling on concrete surface using inverse conduction problem algorithm,” Process Safety and Environmental Protection, vol. 147, pp. 45-54, 2021.
[https://doi.org/10.1016/j.psep.2020.09.032]

-
S. S. Kutateladze, Heat Transfer in Condensation and Boiling, U.S. Atomic Energy Commission, Technical Information Service, 1959.
[https://doi.org/10.1007/978-1-4899-4902-8_9]

-
E. K. Kalinin, I. I. Berlin, V. V. Kostyuk, and E. M. Nosova, “Heat transfer in transition boiling of cryogenic liquids,” Advances in Cryogenic Engineering, vol. 21, pp. 273-277, 1975.
[https://doi.org/10.1007/978-1-4757-0208-8_35]

-
P. J. Berenson, “Film-boiling heat transfer from a horizontal surface,” Journal of Heat Transfer, vol. 83, no. 3, pp. 351-356, 1961.
[https://doi.org/10.1115/1.3682280]

- B. P. Breen and J. W. Westwater, “Effect of diameter of horizontal tubes on film boiling heat transfer,” Chemical Engineering Progress, vol. 58, no. 7, pp. 67-72, 1962.
-
L. -D. Nguyen, M. Kim, B. Choi, K. Chung, K. Do, and T. Kim, “An evaluation of vaporization models for a cryogenic liquid spreading on a solid ground,” International Journal of Heat and Mass Transfer, vol. 146, 118848, 2020.
[https://doi.org/10.1016/j.ijheatmasstransfer.2019.118848]

-
O. Basha, T. Olewski, L. Vechot, M. Castier, and S. Mannan, “Modeling of pool spreading of LNG on land,” Journal of Loss Prevention in the Process Industries, vol. 30, pp. 307-314, 2014.
[https://doi.org/10.1016/j.jlp.2014.04.012]

-
K. Verfondern and B. Dienhart, “Pool spreading and vaporization of liquid hydrogen,” International Journal of Hydrogen Energy, vol. 32, no. 13, pp. 2106-2117, 2007.
[https://doi.org/10.1016/j.ijhydene.2007.04.015]

-
F. Briscoe and P. Shaw, “Spread and evaporation of liquid,” Progress in Energy and Combustion Science, vol. 6, no. 2, pp. 127-140, 1980.
[https://doi.org/10.1016/0360-1285(80)90002-7]

-
P. K. Raj, “Models for cryogenic liquid spill behavior on land and water,” Journal of Hazardous Materials, vol. 5, no. 1-2, pp. 111-130, 1981.
[https://doi.org/10.1016/0304-3894(81)85009-1]

-
L. -D. Nguyen, M. Kim, B. Choi, and K. Chung, “Validation of numerical models for cryogenic-liquid pool spreading and vaporization on solid ground,” International Journal of Heat and Mass Transfer, vol. 128, pp. 817-824, 2019.
[https://doi.org/10.1016/j.ijheatmasstransfer.2018.09.055]

-
L. -D. Nguyen, M. Kim, and K. Chung, “Vaporization of the non-spreading cryogenic-liquid pool on the concrete ground,” International Journal of Heat and Mass Transfer, vol. 163, 120464, 2020.
[https://doi.org/10.1016/j.ijheatmasstransfer.2020.120464]

- M. N. Özisik, Heat Conduction, 1st Edition: John Wiley & Sons Inc., 1980.
- H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, 2nd Edition: Oxford: Clarendon Press, 1959.
-
E. G. Brentari, P. J. Giarratano, and R. V. Smith, Boiling Heat Transfer for Oxygen, Nitrogen, Hydrogen, and Helium, Technical Note 317, U. S. Department of Commerce National Bureau of Standards, 1965.
[https://doi.org/10.6028/NBS.TN.317]