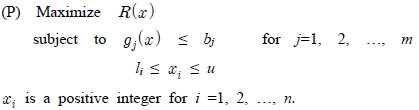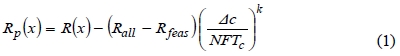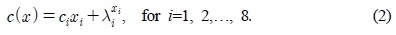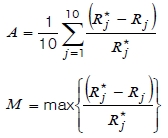An efficient metaheuristic for multi-level reliability optimization problem in electronic systems of the ship

Acronyms

RAP   Redundancy allocation problem

MRAP   Multi-level RAP

GA     Genetic algorithm

TS      Tabu search

ACO     Ant colony optimization

SA      Simulated annealing

VNS      Variable neighborhood search

PSO       Particle swarm optimization

HM     Hybrid metaheuristic

TSMRAP Our tabu search for MRAP

Nomenclature

n    The number of basic items

m    The number of constraints

x_i    The number of redundancy allocated to the ith basic item

R (_x)      The system reliability

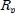(_x)    The penalty function of the system reliability

g_i (_x)   The jth constraint function

r_i     The reliability of the ith basic item

c_i     The cost of the ith basic item

b_j     The amount of allowable resource i

l_i      The lower bound of x_i

u_i     The upper bound of x_i

1. Introduction

Reliability is considered to be one of most important design measures in various systems. Suppose that we want to maximize the system reliability by allocating redundancy units under constraints on cost, volume, weight and other variables in the system design phase. In addition, we have various information to components, parts, some modules and sub-systems which can be used to design our system. The basic problem is that it is difficult to satisfy the required system reliability with basic modules and components. Thus, we should consider redundant units to improve system reliability as a parallel structure. Redundancy allocation has been used mainly to enhance system reliability. The RAP ([1][2]) which involves selecting redundancy levels at each subsystem in order to maximize system reliability under several resource constraints, is a well-known combinatorial optimization problem. The problem arises frequently in system designs such as semi-conductor integrated circuits, nanotechnology, and most electronic systems of the ship. The RAP has various system structures such as series, series-parallel, complex network, k-out-of-n, and so on [3]. In this paper, we restrict ourselves to series-parallel system.

Solutions for the series-parallel RAP have been suggested by many authors. Fyffe et al. [4] originally set up the problem and suggested a solution algorithm utilizing a dynamic programming approach. Nakagawa and Miyazaki [5] developed 33 variations of Fyffe’s problem, where the weight constraint varied its value from 159 to 191. Coit & Liu [6] proposed zero-one integer programming for small size of problems. They constrained the solution space so that only the identical component type can be allowed for each subsystem. On the contrary, Coit & Smith [7] extended Fyffe’s problem in such a way that the parallel system could be more flexible. They allowed a mixing of component types within a subsystem and employed a GA to obtain optimal solutions. Better solutions have been presented by TS (Kulturel-Konak et al. [8][9]), ACO (Liang & Smith [10]), VNS (Liang & Chern [11]), and HM (Nahas et al. [12], Ouzineb et al. [13]). The above all metaheuristics proposed for only best solutions for 14-subsystem problems without referring to their global optimal solutions. However, Kim & Kim [14] suggested the global optimal solutions for these problems by the transformation of binary integer programming, and also showed that all solutions suggested by TS [9] for the 14-subsystem problems were the global optimum. For lager problems with up to 56-subsystem, Bae et al. [15] proprosed SA as a solution method and compared metaheuristics with global optimal solutions.

In the meanwhile, Yun & Kim [16] proposed a new kind of RAP, that is, MRAP. The traditional RAP is to consider only the component redundancy at the lowest-level. MRAP is to consider all cases of the redundancy for system, module, and component levels. A system can be functionally decomposed into system, module, and component levels. Modular redundancy can be more effective (see Boland & EL-Neweihi [17]) than component redundancy at the lowest-level because in modular systems, duplicating a module composed of several components can be easier, and requires less time and skill, than duplicating each component. Therefore the lower the level of the redundant item and the more spare parts added, the higher the cost of redundancy. Kumar et al. [18] studied a similar problem in which more complex structures are also included and proposed a hierarchical GA. Yun et al. [19] considered the extended problem (multiple MRAP) and proposed a GA. Kim & Jang [20] proposed a modified tabu search for the RAP of complex systems.

In this paper, we consider a MRAP in which all cases of redundancy for system, module, and component levels are considered. A TSMRAP of memory based mechanisms that balances intensification with diversification via the short-term and long-term memory is proposed for its solution. To the best of our knowledge, this is the first attempt to use a TS for MRAP. Our TSMRAP is compared with the previous GA [16] for MRAP on the new composed test problems as well as the benchmark problems from the literature. Computational results show that the TSMRAP outstandingly outperforms the GA for almost all test problems.

This paper is organized as follows. In Section 2, we explain the formulation of the presented model. The developed metaheuristic method, TSMRAP, is illustrated in Section 3. An example of MRAP’s superior solution to the traditional RAP is studied and computational results from several numerical experiments are discussed in Section 4. We conclude in Section 5 with some suggestions for further research.

2. Problem formulation

In MRAP, the number of available redundancy structure increases exponentially as the size of problem becomes large. In this paper, two assumptions are set up to exclude impossible redundancy structures (Yun et al. [19]).

Assumptions:

1) The combination of the basic items for redundancy should satisfy the function at the system level. If a basic item is used, all its sibling items should be used or its function should be satisfied by corresponding child items.

2) The basic items for redundancy should be used in parallel at one combination.

The problem objective is to maximize system reliability, R (x), given constraints on the system, only for system cost in this paper. The system is configured as a series-parallel system. The MRAP optimization model can be generally formulated as the following nonlinear integer programming problem:

This problem was proven to be a NP-hard problem (Chern [21]). We refer interested readers to Yun & Kim [16] for the detailed formulation of MRAP.

3. TS algorithm

In this paper, we propose a TS called the TSMRAP which is based on the TS [8] algorithm for the series-parallel RAP.

3.5 The structure of generating the neighborhood Solutions

In TSMRAP, neighborhood solutions are generated by two moves, that is, the first and second move. The first move is similar to the TS [8] for the series-parallel system, that is, to change the allocated redundant number of the module or component by adding or subtracting one. The second move is somewhat more complicated than the first move due to the characteristics of the problem. The scheme of the second move is to replace the current solution with the redundant value of the module or component. That is, if the current solution within a subsystem is assigned to the module, then it is replaced with a series of the component. Reversely, if the current solution within a subsystem is assigned to the component, then it is replaced by the module.

For example, let us consider the following system structure with 2 modules and 5 components in Table 1. The cost function is as follows.

Table 1:

An example with two modules

The cost limit is set to 95. Suppose that the current solution during the iterations of TSMRAP to obtain the optimal solution for our problem to be given in Table 2, that is, the encoding status of (2, 0, 0, 0, 0, 2, 1, 0, 0). From the current solution, all the neighborhood solutions generated by the two moves are shown in Table 2. The number of the neighborhood solutions by the first move (adding or subtracting one) are 5 cases shown in Table 2. In the first move, notice that when the redundant value of component (122) equals to 1, it is not allowed to subtract one from the component (122).

Table 2:

All the neighborhood solutions by two moves

The scheme of the second move is to replace the current solution with the redundant value of the module or component. The number of the neighborhood solutions generated by the second move is 4 cases. As shown in Table 2, when the value of module (11) equals to 2, it is replaced with two cases of components (111, 112, 113), that is, (1, 1, 1) and (2, 2, 2). Namely, it is allowed to assign a series of the redundant value of components up to the value of the redundant number of module (11), that is, 2. Reversely, when the value of component (121, 122) equals to (2, 1), it is replaced with two cases of module (12), that is, 1 and 2. We assign the redundant value of module up to the maximum value of the redundant number among components (121) and (122), that is, 2.

In Table 2, the system reliability for each neighborhood solution is evaluated by the penalty function of Eq. (2). For example, (2, 0, 0, 0, 0, 2, 2) has the penalty value of 0.796362 instead of 0.895469. Among 9 candidates of neighborhood solutions, (2, 2, 0, 0, 0, 0, 0), which has the maximum value of the system reliability (0.852996), is selected for the next best move of TSMRAP.

4. An example and computational results

In this section, we conduct three experiments. First, we mention the possibility of having MRAP’s superior solutions to the traditional RAP. Second, we compare the proposed TSMRAP and the previous GA for three cases of levels. Finally, we evaluate the performance of metaheuristics for additional 120 test problems for moderate size of system structure.

4.1 An example of MRAP’s superior solutions to the traditional RAP

We compare the traditional RAP of considering only the component redundancy for the lowest-level with MRAP of allowing the modular and the component redundancy. We consider the 3-level system. Table 3 gives the values of input variables for reliability, price, and additive cost parameter. Test problems are generated by varying the cost limit from 150 to 340. A comparison between the traditional RAP and MRAP is shown in Table 4. As the results in Table 4 indicate, MRAP provides the superior solutions to the traditional RAP for 19 cases of 20 test problems. For only one case (cost limit of 190), the traditional RAP and MRAP have the same result of 0.8878.

Table 3:

The input data for 3-level system

Table 4:

A comparison of the traditional RAP and MRAP

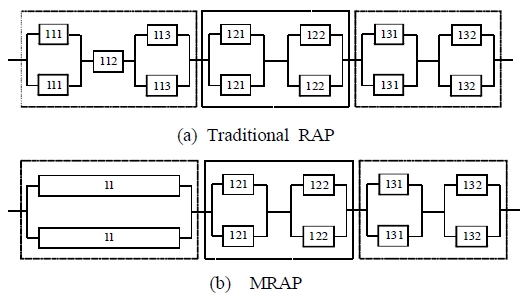
Specifically, for the cost limit of 170, both of the system structuresare shown in Figure 1. In this case, the optimal solution of the traditional RAP and MRAP are given by 0.8455 and 0.8511, respectively. This result indicates that MRAP considering the modular redundancy as well as the component redundancy at the lowest-level provides the possibility of having the better system reliability than the traditional RAP of considering only the component redundancy.

Figure 1:

The system structure

4.2 Computational results

To additionally evaluate the performance of the previous GA[16] and the proposed TSMRAP, the new test problems for moderate size of system structure are designed. They are composed of 4 sets of 10 test problems for each level, that is, totally 120 test problems. For the case of 3-level, we replicated the data in Table 3 by h-fold, where h ranges from 4, 6, 8, to 10, that is, the number of subsystems of each problem became n=3 × h (h=4, 6, 8, and 10). Similarly, for the cases of 4-level, the number of subsystems of each problem became n=2 × h (h =6, 9, 12, and 15). For each set, 10 test problems were generated according to increase the cost limit of the constraint by 100. We increase the cost limit(C) of the constraints appropriately for each problem according to the size of problems in order to assign the reasonable value (not to be very low) of system reliability for each problem. In our numerical experiments, the stopping criterion of TSMRAP was defined as 200 iterations without finding an improvement in the best feasible solution. TSMRAP was applied 5 times with different starting initial solutions for each test problem. The computational results for evaluating the performance between GA and TSMRAP are summarized in Table 5. Two algorithms are coded in C/C++, and experiments are performed on a Pentium IV 3.0 GHz PC. Performances of GA and TSMRAP are assessed in terms of average relative error(A), maximum relative error(M), optimality rate(O) and average execution time(sec.) of 10 problems(T) defined as follows.

O = the number of cases in which each method yields the best solution among 10 problems.

R_j = the system reliability obtained by each method for test problem j.

R_j^*= the best system reliability obtained by both of GA and TSMRAP.

Table 5:

Computational results of GA and TSMRAP

As the results in Table 5 indicate, TSMRAP outstandingly outperformed the GA. TSMRAP obtained a higher system reliability in 115 of 120 test cases. TSMRAP failed to obtain the best solution for only two cases in the case of n=30 for 4-level. Even for these cases, the average relative error (A) of GA is very poor, scoring the higher value of 0.0356 than 0.0016 of TSMRAP. GA obtained totally the best solution in only 5 cases, in which two cases are the higher system reliability than TSMRAP and 3 cases are the same system reliability of TSMRAP.

In terms of computing time, GA and TSMRAP are nearly equal for the case n=12 and 18 of 3-level and 4-level. For the cases (n=24 and 30) of 3-level and 4-level, TSMRAP is generally faster than GA. Specifically, when n=30 of 3-level and 4-level, the computing time of GA is almost 3 times of TSMRAP’s.

5. Conclusions

The RAP has usually considered only the component redundancy at the lowest-level for the enhancement of system reliability. A system can be functionally decomposed into system, module, and component levels. Modular redundancy can be more effective than component redundancy at the lowest-levelbecause in modular systems, duplicating a module composed of several components can be easier, and requires less time and skill. This paper dealt with a MRAP in which all cases of redundancy for system, module, and component levels are considered. A TSMRAP of memory-based mechanisms that balances intensification with diversification via the short-term and long-term memory was proposed for its solution. To the best of our knowledge, this is the first attempt to use a TS for MRAP. Our TSMRAP was compared with the previous GA for MRAP on the new composed test problems as well as the benchmark problems from the literature. Computational results showed that the TSMRAP outstandingly outperformed the GA for almost all test problems.

For the further research, we will consider various RAPs, develop efficient metaheuristics and compare their performance. Even if we consider the static RAP, the RAP in dynamic reliability cases may be a promising area and in that case, operations problem can also be considered together with RAP.

References

• W. Kuo, V. R. Prasad, F. A. Tillman, and C. L. Hwang, “Optimal reliability design: Fundamentals and Applications”, Cambridge University Press, (2001).
• W. Kuo, and V. R. Prasad, “An annotated overview of system-reliability optimization”, IEEE Transactions on Reliability, 49(2), p176-187, (2000).
• W. Kuo, C. L. Hwang, and F. A. Tillman, “A note on heuristic methods in optimal system reliability”, IEEE Transactions on Reliability, 27(5), p320-324, (1978).
• D. E. Fyffe, W. W. Hines, and N. K. Lee, “System reliability allocation and a computational algorithm”, IEEE Transactions on Reliability, 17(2), p64-69, (1968). [https://doi.org/10.1109/TR.1968.5217517]
• Y. Nakagawa, and S. Miyazaki, “Surrogate constraints algorithm for reliability optimization problems with two constraints”, IEEE Transactions on Reliability, 30(2), p175-180, (1981). [https://doi.org/10.1109/TR.1981.5221024]
• D. E. Coit, and J. Liu, “System reliability optimization with k-out-of-n subsystems”, International Journal of Reliability, Quality and Safety Engineering, 7(2), p129-142, (2000). [https://doi.org/10.1142/S0218539300000110]
• D. E. Coit, and A. E. Smith, “Reliability optimization of series-parallel systems using a genetic algorithm”, IEEE Transactions on Reliability, 45(2), p254-260, (1996). [https://doi.org/10.1109/24.510811]
• S. Kulturel-Konak, A. E. Norman, and D. W. Coit, “Efficiently solving the redundancy allocation problem using tabu search”, IIE Transactions, 35(6), p515-526, (2003). [https://doi.org/10.1080/07408170304422]
• S. Kulturel-Konak, B. A. Norman, D. W. Coit, and A. E. Smith, “Exploiting tabu search memory in constrained problems”, INFORMS Journal on Computing, 16(3), p241-254, (2004). [https://doi.org/10.1287/ijoc.1030.0040]
• Y. C. Liang, and A. E. Smith, “An ant colony optimization algorithm for the reliability allocation problem problem (RAP)”, IEEE Transactions on Reliability, 53(3), p417-423, (2004).
• Y. C. Liang, and Y. C. Chen, “Redundancy allocation of series-parallel systems using a variable neighborhood search algorithm”, Reliability Engineering and System Safety, 92(3), p323-331, (2007). [https://doi.org/10.1016/j.ress.2006.04.013]
• N. Nahas, M. Nourelfath, and D. Ait-Kadi, “Coupling ant colony and the degraded ceiling algorithm for the redundancy allocation problem of series-parallel systems”, Reliability Engineering and System Safety, 92(2), p211-222, (2007). [https://doi.org/10.1016/j.ress.2005.12.002]
• M. Ouzineb, M. Nourelfath, and M. Gendreau, “An efficient heuristic for reliability design optimization problems”, Computers and Operations Research, 37(2), p223-235, (2010). [https://doi.org/10.1016/j.cor.2009.04.011]
• J. H. Kim, and J. S. Kim, “Globally solving the redundancy allocation problem for the case of series-parallel systems”, Proceedings of the 2nd Asian International Workshop of Advanced Reliability Modeling Ⅱ, p150-157, (2006). [https://doi.org/10.1142/9789812773760_0018]
• C. O. Bae, H. G. Kim, J. H. Kim, J. Y. Son, and W. Y. Yun, “Solving the redundancy allocation problem with multiple component choices using metaheuristics”, International Journal of Industrial Engineering, 14(4), p315-323, (2007).
• W. Y. Yun, and J. W. Kim, “Multi-level redundancy optimization in series systems”, Computers and Industrial Engineering, 46(2), p337-346, (2004). [https://doi.org/10.1016/j.cie.2003.12.013]
• P. Boland, and E. EL-Neweihi, “Component redundancy vs. system redundancy in the hazard rate ordering”, IEEE Transactions on Reliability, 44(4), p614-619, (1995). [https://doi.org/10.1109/24.475980]
• R. Kumar, K. Izui, Y. Masataka, and S. Nisiwaki, “Multilevel redundancy allocation optimization using hierarchical genetic algorithm”, IEEE Transactions on Reliability, 57(4), p650-661, (2008). [https://doi.org/10.1109/TR.2008.2006079]
• W. Y. Yun, Y. M. Song, and H. G. Kim, “Multiple multi-level redundancy allocation in series systems”, Reliability Engineering and System Safety, 92(3), p308-313, (2007). [https://doi.org/10.1016/j.ress.2006.04.006]
• J. H. Kim, and K. W. Jang, “A modified tabu search for redundancy allocation of complex systems of ships”, Journal of the Korean Society of Marine Engineering, 38(2), p225-232, (2014). [https://doi.org/10.5916/jkosme.2014.38.2.225]
• M. S. Chern, “On the computational complexity of reliability redundancy allocation in a series system”, Operations Research Letters, 11(5), p309-315, (1992). [https://doi.org/10.1016/0167-6377(92)90008-Q]