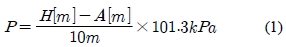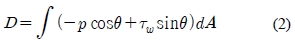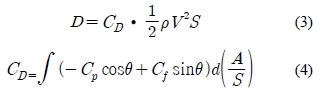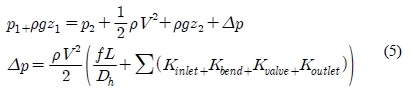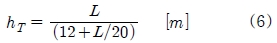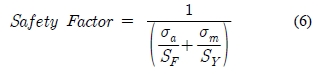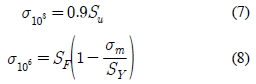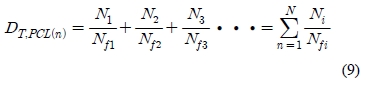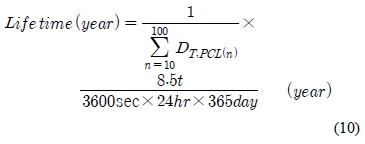Variation of the structural stability for the sonar dome window in a naval vessel according to the state of the drain valve
Since the active sonar for a naval vessel is usually installed in a bulbous bow, GRP(Glass reinforced plastic) material with low density and high strength is used for the material of the sonar dome window in order to prohibit impact by slamming wave or foreign material in the sea.
The structural safety of the sonar dome is varied according to the interior and exterior distributed pressure on the sonar dome. Therefore, the variation of the structural safety according to the pressure variation of the sonar dome window caused by the drain valve state is studied by CAE
초록
수상함정에 사용되는 능동소나는 통상적으로 구상선수부에 설치하게 된다. 따라서 구상선수부에 설치된 소나의 항해 중 유체력 및 수중 부유물에 의한 충돌 파손을 막기 위해 밀도가 낮으면서 강도가 높은 복합소재 재질의 소나돔 윈도우를 설치하게 된다. 외부 유체력 및 충격 발생 시 소나돔 윈도우의 안정도는 소나돔 윈도우 내외부의 압력 분포에 따라 달라지므로 본 연구에서는 소나돔 충, 배수 밸브의 상태에 따른 소나돔 윈도우의 내외부 압력변화를 해석적으로 검토하고 이에 따른 응력변화를 파악하고자 한다.
Keywords:
Sonar dome window, Hydrodynamic force, Slamming, Soderberg plot, Life cycles, 소나돔윈도우, 유체저항력, 슬래밍, Soderberg 선도, 수명1. 서 론
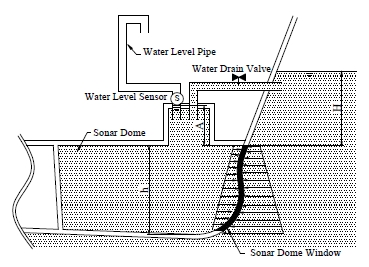
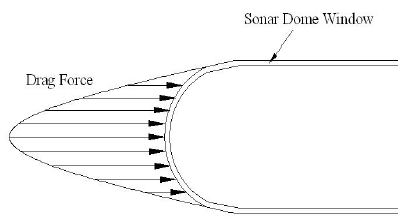
함정에 있어 수중 탐지 및 식별은 함의 생존성과 직결된 매우 중요한 성능 중 하나이다. 특히 최근 건조되는 함정의 경우 능동소나를 구상 선수(bulbous bow)에 설치하여 운용하고 있다. 이러한 능동소나의 경우 선수부에 위치하기 때문에 항해 중 유체의 항력(drag force), 파도에 의한 슬래밍(slamming) 충격력, 부유물에 의한 충돌 등으로 인한 소나 시스템의 파손을 막기 위해 Figure 1과 같이 커버를 부착하게 되며 이를 소나돔 윈도우(sonar dome window)라고 부른다.
이러한 소나돔 윈도우의 경우 밀도가 높고 강도가 높은 재질을 사용하게 되면 음향투과손실 증가로 인해 소나의 탐지성능 저하를 초래하므로 일반적으로 밀도가 낮은 고무나 GRP(glass reinforced plastic)와 같은 복합소재 재질이 주로 사용된다.
이와 같이 소나돔 윈도우는 선체에 비해 약한 재질로 제작될 수밖에는 없으나 유체력 등 저항을 가장 많이 받는 선수부에 설치되므로 수중 부유물, 슬래밍 등에 의한 파손이 발생 될 수 있다. 따라서 소나돔 윈도우 제작 시 음탐성능에 영향을 미치지 않는 범위 내에서 이러한 유체력에 대해 충분히 내구성을 가지도록 설계가 진행되고 있으며 유체력과 선체 내구성 관련하여 많은 연구가 이루어지고 있다[1]-[5].
본 연구에서는 소나돔 윈도우의 운용에 있어 소나돔 내부의 압력을 조정하는 해수 관리 시스템(water management system)에 따른 소나돔 윈도우의 압력분포를 일반 항해 조건 및 슬래밍 발생 시에 대해 파악하여 소나돔 윈도우의 구조 안정성을 파악하고자 한다.
2. 소나돔 윈도우의 하중분포
소나돔의 경우 내부에 해수를 충수시켜 작동하기 때문에 선수부에 충, 배수 밸브가 설치되어 소나돔으로 충수 및 배수를 수행하게 된다. 소나돔에 해수를 완충시킨 이후 소나돔의 충, 배수 밸브의 개폐여부에 따라 소나돔 내부의 압력은 정박 및 항해 중 달라지므로 이러한 밸브 상태는 소나돔 윈도우에 걸리는 압력을 변화시킨다. 따라서 본 절에서는 소나돔 윈도우에 걸리는 압력이 충, 배수 밸브의 개폐 여부에 따라 얼마만큼 달라지는지 파악해 보고자 한다.
2.1 수압에 의한 압력
소나돔은 Figure 2와 같이 구상 선수부에 설치된다. 여기서 충, 배수 밸브가 개방되어 있을 경우 밸브 외부 및 내부의 유체는 서로 연결되어 수압 레벨 배관(Water level pipe)의 높이 조절을 통해 자동으로 정적 평형을 이루기 때문에 소나돔 윈도우에는 수압이 발생하지 않으며 모든 수압은 소나돔 내부의 선체부에서 받게 된다. 하지만 밸브를 닫을 경우 소나돔 내부는 Figure 2에서와 같이 소나돔 내부의 수위(“A”m)에 대한 수압이 걸리지만 소나돔 외부의 경우 수면에서부터 소나돔까지의 수위(“H”m)에 대한 수압이 발생되므로 소나돔 윈도우에는 내, 외부 수위차이 만큼의 수압이 발생되게 된다. 여기서 소나돔의 높이를 "h"라고 할 경우 소나돔 윈도우의 하부와 상부는 이 높이만큼의 압력 구배를 가지게 되지만 내외부의 압력 차이는 식 (1)과 같이 해수면과 소나돔 탱크 내의 수면과의 차이만큼의 수압으로 일정하게 걸리게 된다.
여기서 P는 수압, H는 수면에서 소나돔 윈도우 상부까지의 거리, A는 해수레벨 배관내의 해수면에서 소나돔 윈도우 상부까지의 거리이다.
2.2 유체에 의한 항력 및 내부압력
이동하는 유체에 잠겨있는 물체, 또는 정지된 유체에 물체가 움직일 경우 유동방향으로는 항력(drag force)이 발생하며 익형 단면과 같이 단면이 비대칭일 경우 속도차이로 발생한 압력 차이에 의한 양력(lift force)이 발생한다.
최대속도로 선박이 항해한다고 가정할 경우소나돔이 위치해 있는 선수부의 항력은 식 (2)와 같이 나타낼 수 있다.
여기서 D는 항력, p는 표면압력, τω는 유동에 의해 발생한 표면 전단응력, θ는 회전방향에 대한 항력을 받는 면의 각도, A는 항력을 받는 면의 면적이다.
또한 항력은 항력계수(drag coefficient)를 이용하여 식 (3)과 같이 나타낼 수 있으며 항력계수는 식 (4)와 같다. 식 (4)에서 항력계수는 압력계수와 표면 마찰계수를 가지고 표현할 수 있으며 속도가 빠를 경우 점성에 의한 효과를 무시할 수 있는 무점성 유동(inviscid flow)으로 가정할 수 있으므로 식 (4)에서 표면마찰계수 Cf는 무시할 수 있다.
여기서 CD는 항력계수, V는 유체의 속도, ρ는 유체의 밀도, S는 유체력을 받는 면의 면적, Cp는 압력계수, Cf는 표면마찰계수이다.
함정의 소나돔은 일반적으로 구상 선수(bulbous bow)부에 설치되므로 Figure 3과 같이 소나돔에 작용하는 항력은 해수와 수직으로 부딪치는 중심부에서 최대가 되며 구상의 끝부분에서는 유체의 점성을 무시할 경우 항력은 거의 없다고 볼 수 있다.
소나돔의 해수 밸브가 열려 있을 경우 항해 중 내부 압력은 Bernoulli 식으로부터 식 (5)와 같이 나타낼 수 있으며 배관의 마찰손실 및 밸브 손실팩터, 입출구 손실팩터 등으로 인해 압력강하가 발생하게 된다
여기서 p1, p2는 소나돔 외, 내부 압력, z1, z2는 소나돔 외, 내부 수두, V는 배관에서 유입되는 해수 속도, ∆p는 압력강하, f는 마찰 계수(friction fac-tor), Dh는 배관직경, L은 배관길이, Kinlet, Kbend, Kvalve, Koutlet은 입구, 벤딩부, 밸브 및 출구의 손실계수이다
소나돔 제작사의 유동해석 결과로부터 밸브 개방 상태에서 소나돔 윈도우 중심의 정체점(stagnation point)에서 항력에 의해 걸리는 압력은 약 204kN/m2이며 내부압력은 약 68kN/m2 임을 알 수 있었다. 여기서 내,외부 압력은 일반적인 값이 아니며 본 연구에서 다루는 특정 함정의 해석값이다. 또한 소나돔 윈도우 해수 밸브를 잠글 경우 소나돔 윈도우의 내부 압력은 소나돔 윈도우에 채워져 있는 해수에 의한 수압이며, 외부 압력은 해수 유체흐름에 의한 항력(204kN/m2~0kN/m2) 및 수면으로부터 소나돔 윈도우까지의 수압이 걸리게 된다.
2.3 슬래밍(Slamming)에 의한 압력
슬래밍은 해상 상태가 매우 나쁜 상태에서 함이 항해할 때 입사파도와 선체간의 큰 상대운동으로 인해 선체가 수면 밖으로 나왔다가 재입수하는 과정에서 발생하는 심각한 충격 현상을 말한다. 이러한 슬래밍은 다음의 4단계 과정으로 구성된다.
(Step 1) 수면 위로 선체 앞부분이 빠져나옴
(Step 2) 선체 앞부분이 수면으로 들어가면서 해수면과 충돌발생(BV 기준(6) :210 kN/m2, 30도 각도도 가압)
(Step 3) 선체부가 물속으로 가속하며 진입(내부 물의 충격 가속력 = 소나돔 내부압력 × Dynamic Factor)
(Step 4) 선체부가 물속으로 입수하면서 수압 발생
Step 1의 경우 소나돔 윈도우의 압력은 소나돔 내부 해수의 가속력에 의한 힘으로 일반적으로 크지 않기 때문에 무시한다. Step 2의 경우 BV 1040(6)에 따라 210kN/m2의 압력이 소나돔 윈도우 하부에 수면의 수직선에서 30도 각도로 작용한다고 가정하고 있다. 슬래밍 발생 시 소나돔 윈도우에 작용하는 압력은 내부압력이 내부에 채워져 있는 해수의 양에 따라 달라지므로 슬래밍 발생 시 충수 밸브 개폐에 따라 발생하는 수두 차이만큼 차이나게 된다. Step 3에 대해 동적계수(dynamic factor)는 소나돔 제작사에서 제시한 2.65를 사용하였다. 여기서 해수 충,배수밸브의 개폐에 따라 소나돔 내부 해수의 양은 크게 차이나지 않으므로 이로 인한 차이는 거의 없다고 가정하였다. Step 4 시에는 소나돔 해수 밸브가 개방되어 있을 경우 소나돔 내외부의 수압이 같기 때문에 소나돔 윈도우에는 수압이 걸리지 않으므로 이때 소나돔 윈도우에 걸리는 힘은 유체의 저항력에 따른 유체력과 이에 따른 내부압력이 발생한다. 하지만 밸브를 잠근 상태일 경우 유체의 저항력에 따른 유체력에 추가로 수면에서 소나돔 윈도우까지의 수두가 식 (6)과 같이 소나돔 윈도우에 걸리게 되며 슬래밍 발생 시 동적 효과를 고려하여 수압은 식 (6)의 수두 대비 1.6배 추가로 고려하도록 제시하고 있다[6].
여기서 hΤ는 항해 중 수두(m), L은 선체 길이이다.
따라서 밸브 잠금 시 소나돔 윈도우에 걸리는 수압은 해상상태가 매우 나쁠 경우 슬래밍 발생 등으로 인해 흘수가 급격히 변화하면서 무시하지 못할 수준의 수압으로 인한 응력이 소나돔 윈도우에 발생할 수 있다.
3. 수치해석
본 절에서는 2절에서 정의한 힘에 대해서 현재 운용중인 특정 함정의 소나돔 윈도우를 가지고 다음의 3가지 경우에 대해 소나돔 충,배수 밸브의 상태에 따라 정적해석을 수행하였다.
(Case 1) : 정박 중 해수 유입 밸브 잠금 상태
(Case 2) : 최대속도 일반 항해 중 해수 유입 밸브 계폐
(Case 3) : 최대속도 슬래밍 발생 시 해수 유입 밸브 계폐
3.1 유한요소모델
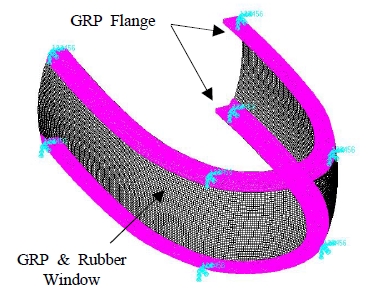
소나돔 윈도우의 정적해석 수행을 위해 유한요소 모델을 Figure 4와 같이 MSC. Patran을 이용하여 모델링하였다. Figure 4에서 소나돔 윈도우의 선체 체결부는 모두 완전 구속조건으로 처리하였다. 소나돔 윈도우는 GRP 플랜지부, GRP 및 고무 윈도우부로 구성되는데 GRP 플랜지부의 경우 솔리드 사면체 요소를 사용하여 모델링하였으며 GRP 윈도우부는 사각형 셀 요소로, 고무 윈도우부는 GRP 윈도우부 요소에 "Mesh on Mesh" 기능을 이용하여 모델링하였다. 유한요소 수행을 위한 재료 물성은 Table 1과 같다.
3.2 해석결과
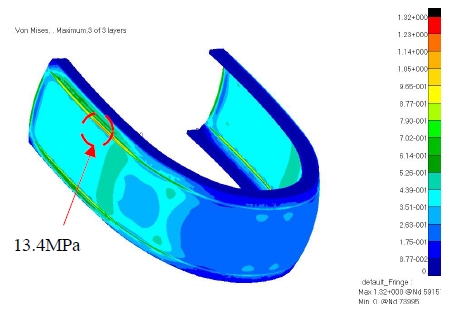
함 정지 상태에서 밸브 잠금 시 Case 1의 수압에 대한 해석 결과 기존 소나돔 윈도우에서 최대응력은 13.4MPa로 Figure 5와 같으며 소나 윈도우 엣지부인 GRP 연결부에서 가장 큰 응력이 발생함을 알 수 있었다. 여기서 기본 수압은 흘수 6.7m, 소나돔 내부 수두 1.3m인 조건을 적용하여 총 5.4m 수압조건에서 수행하였다. 밸브 개방 시에는 내부, 외부 압력이 같아지므로 소나돔 윈도우에는 수압이 발생하지 않는다.
수압을 받는 선체의 경우 수압증가로 인한 좌굴(buckling) 발생 가능하기 때문에 선형해석에 추가로 좌굴해석을 수행하였다. 좌굴해석 결과 5.4m 수압조건에서 좌굴에 대한 안전율은 1.84임을 알 수 있었으며 9.94m 이상 수압차가 발생할 경우 좌굴이 발생될 수 있음을 파악할 수 있었다.
소나돔 윈도우 제작사의 유동 해석 결과 최대 항해 중 유체 저항력에 의한 압력은 최대 204kN/m2이며 이 유체력은 Figure 3과 같이 선수에서 선미방향으로 갈수록 선형적으로 감소한다고 가정하였다. 최대속도 항해 중 해수 유입 밸브의 개폐에 따른 소나돔 내외부 압력변화는 Table 2와 같다. Table 2와 같이 밸브 개방 시에는 내부 압력으로 인해 소나윈도우에 작용하는 최대 압력은 68kN/m2으로 가정하였으며 소나돔 윈도우에서 항력의 영향을 크게 받지 않는 후미부의 경우 내부압력으로 인해 (-) 방향(선체 외부 방향)의 압력이 발생하게 된다.

Internal/External pressure of the sonar dome according to the state of the drain valve at max. speed sailing condition
하지만 밸브 잠금 시 내부압력은 소나돔 내부 해수에 의한 수압만이 걸리게 되며 최종적으로 유체 저항력에 내외부 수압차에 의한 압력이 소나돔 윈도우에 작용하게 된다.
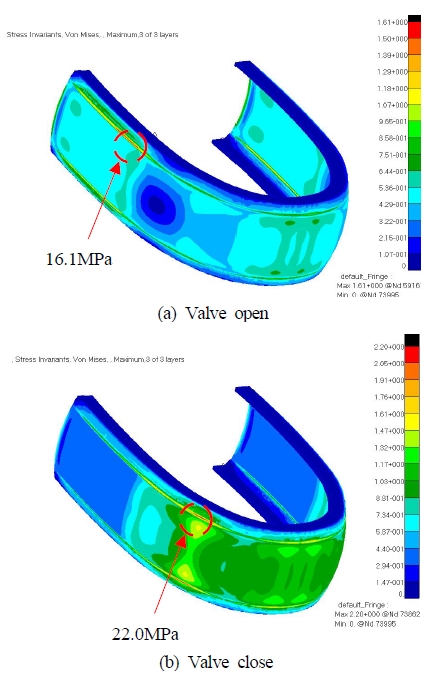
해석 결과 밸브 개방 상태에서 기존 소나돔에서의 최대응력은 16.1MPa로 Figure 6과 같으며 소나 윈도우 상하부 GRP 연결부에서 가장 큰 응력이 발생함을 알 수 있었다. 밸브 잠금 상태에서 최대응력은 22.0MPa로 밸브 개방 상태 대비 약 37% 증가함을 알 수 있었으며 최대응력부가 소나돔 윈도우의 선수 측으로 이동함을 파악할 수 있었다.
2.3절에서 언급한 바와 같이 슬래밍 발생 시 과정은 총 4 Step으로 구성되는데 Step 1, 3의 경우 밸브 개방, 잠금에 따라 내,외부 압력 변화에 큰 차이가 없으나 Step 2, 4의 경우 Table 3과 같이 밸브 개방, 잠금에 따라 내,외부 압력 변화가 발생한다.
소나돔 윈도우의 슬래밍 Step 2에서의 밸브 개폐에 따른 정적해석은 BV 1040에 따라 슬래밍 충격 시 압력을 210kN/m2으로 하여 입수각은 수직 기준으로 30도 각도로 적용하였다.
밸브를 개방하였을 때 소나돔 내부압력은 흘수(6.7m 기준)만큼의 수압을 유지하고 있으며 외부 충격 압력에 대해 최대 응력은 Figure 7(a)와 같이 30.8MPa임을 알 수 있었다. 밸브를 잠글 경우 소나돔 내부압력은 수압 레벨 배관의 수두높이(1.3m) 만큼의 수압을 유지하고 있으며 외부 충격 압력에 대해 최대 응력은 Figure 7(b)와 같이 39.1MPa로 밸브 개방 상태 대비 약 27% 증가함을 알 수 있었다.
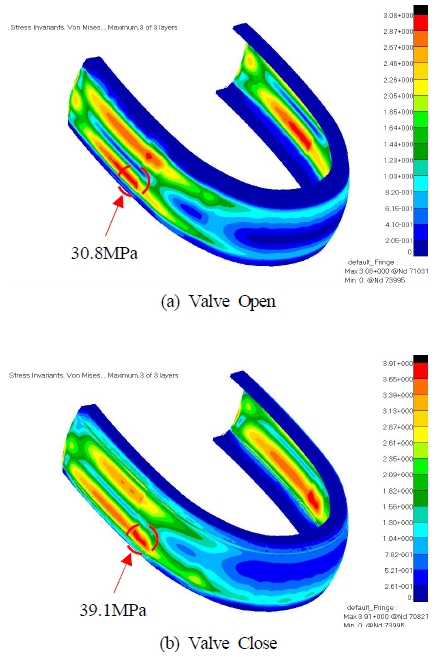
Von Mises stress distribution under the slamming step 2 condition(Valve open : Max=30.8MPa, valve close : Max=39.1MPa)
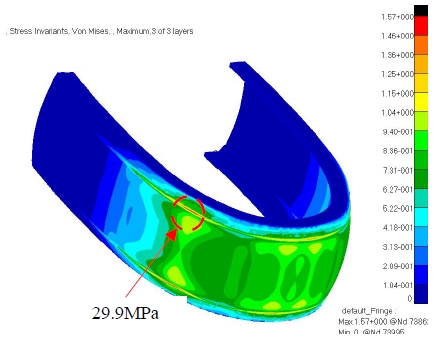
소나돔 윈도우의 슬래밍 Step 4에서의 밸브 잠금 시 정적해석 결과는 Figure 8과 같다. 밸브 개방 시는 3.2.2절의 일반 최대속도 항해 중 밸브 개방 시와 동일하지만(최대 16.1MPa) 밸브 잠금 시는 함의 동적효과를 고려한 수압의 영향으로 인해 최대응력이 기존의 경우 29.9MPa, 까지 늘어남을 알 수 있었다. 이때 최대응력 발생 지점은 밸브 개방 시 대비 선수부로 이동함을 알 수 있었다. 여기서 밸브 잠금 시 소나돔이 받는 수압은 총 11m로 3.2.1절의 좌굴 하한치를 초과함을 알 수 있다. 따라서 최대응력은 인장강도 대비 낮은 값이지만 좌굴가능성이 존재하는 것으로 파악되었다.
3.3 결과 요약 및 수명평가
항해 중 소나돔에 걸리는 응력에 대해 해수 유입 밸브 상태에 따라 해석을 수행한 결과 해수밸브 개폐 여부에 따라 운항 중 응력은 밸브 잠금 시 약 37% 상승함을 알 수 있었으며 슬래밍 조건인 Case 3-Step 2, 4 상태에서 밸브 개폐에 따라 응력값이 Step 2에서 27% 정도, Step 4에서 86% 정도 차이남을 확인할 수 있었다. 하지만 응력 수준은 인장강도에 비해 충분히 작음을 알 수 있었다.
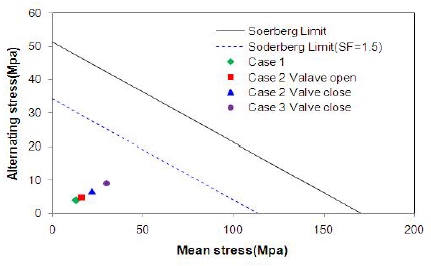
소나돔 윈도우에 작용하는 변동응력의 크기는 평균응력의 30%로 가정하고 해석 결과로부터 Soderberg 선도를 그려보면 Figure 9와 같다. 여기서 변동응력은 일반 항해 중 측정을 통해 경험적으로 산출한 값이다. Figure 9로부터 해석 시 고려한 Case 1, Case, 2 및 Case 3-Step 4의 3가지 경우에 대해 모두 충분히 안전한 영역에 있음을 알 수 있으며 최대속도 운항 시 2.9~6.5의 안전율을 가짐을 알 수 있었다. 여기서 안전율은 식 (6)을 통해 계산하였다.
여기서 σa는 변동응력, σm는 평균응력, SF는 피로한도(106 사이클 응력=0.3 SU), SY는 항복강도, SU는 인장강도(=190MPa)이다
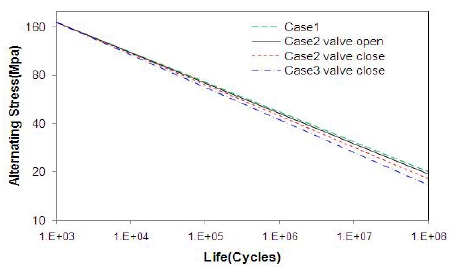
또한 슬래밍 충격 상태인 Case 3-Step 2 조건에서도 밸브 개폐에 따라 안전율이 각각 3.2 및 3.8 정도로 안정성에는 큰 문제가 없음을 파악할 수 있었으며 안전율은 인장강도와 최대응력간의 비로 계산하였다. 해석 결과로부터 GRP의 S-N 곡선을 Figure 10과 같이 정의하고 해석의 3가지 Case에 대해 수명을 계산해보았다.
여기서 103 및 106 사이클에 대한 응력(σ103, σ106)은 식 (7)~(8)과 같다.
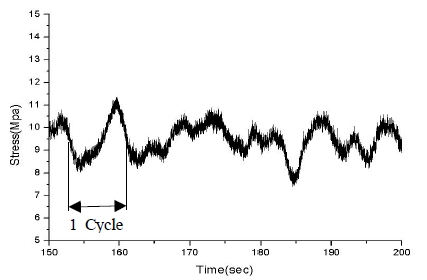
IACS Recommendation 34[7]에서는 북대서양에서 발생하는 파도에 대해 100,000회의 계측을 통해 해상상태에 대한 확률적 모델을 제시하였다. 여기서 주기 8.5초의 파도가 가장 많이 계측되었다. 실제로 Figure 11과 같이 항해 중 소나돔 윈도우의 응력 계측 시 변동응력의 주기는 약 5~10초정도임을 알 수 있다. 소나돔에 발생하는 변동 응력은 파도의 주기에 의존한다고 가정하고 이 주기를 IACS의 조사결과를 바탕으로 가장 확률이 높은 8.5초로 가정하여 수명을 계산하면 모든 경우가 Table 4와 같이 무한 수명을 가짐을 예측할 수 있다. 여기서 수명은 식 (9)~(10)의 Palmgren-Miner의 선형 손상 누적법(linear damage summation law)에 의해 계산 하였다.

Internal/External pressure of the sonar dome according to the state of the drain valve at slamming step 4 condition
여기서 DT,PCL(n)는 속도 "n"에서 “t”초 동안 운항 시 계산된 데미지(total Damage), Ni 는 응력 σi에 대한 실제 카운팅 된 반복 횟수, Nfi 은 응력 σi에 대한 피로 한도이다.
해석 결과로부터 해수 밸브 잠금 상태에서 운항을 하더라도 GRP 재료의 인장강도를 190MPa임을 고려해 볼 때 최대속도 및 슬래밍 조건에서 충분히 낮은 응력으로 인해 파손의 우려가 없으나 슬래밍 발생 시 수중 부유물에 의한 충격 등이 발생 할 경우 밸브 잠금 시 평균응력 증가로 인해 밸브 개방 시 대비 더 불안정한 조건이 될 수 있음을 파악할 수 있었다.
그리고 좌굴관점에서 보았을 때 슬래밍 step 4 조건에서는 밸브 잠금 시 소나돔에 작용하는 수압이 좌굴 하한치를 초과함으로 이로 인한 파손 가능성이 존재함을 파악할 수 있었다.
4. 결 론
본 연구에서는 함정의 소나돔 운용에 있어 충,배수 밸브의 개,폐에 따른 압력 변화가 소나돔의 안정도에 얼마만큼 영향을 미치는지를 해석을 통해 검토하였다. 소나돔 제작사는 소나돔 의 충, 배수밸브를 개방한 상태에서 함을 운용하도록 권고되고 있으며 이 때 소나돔 윈도우에 걸리는 힘은 외부의 유체력과 이로 인한 내부압력의 평형 관계를 통해 결정된다. 하지만 밸브를 잠글 경우, 수압에 의한 영향으로 인해 소나돔 윈도우에 걸리는 압력분포는 밸브 개방 시와 달라진다. 해석결과 일반 해상 조건에서 최대속도 항해 중 밸브 개폐에 따라 최대응력은 크게 달라지지 않으나 최대응력지점이 밸브 잠금에 따라 소나돔의 측면부에서 선수 구상선수부로 이동하게 됨을 알 수 있었다. 특히 슬래밍 발생 시 수면과의 충돌이 발생하는 Step 2 및 선수부가 물속으로 잠기는 Step 4에서 밸브 잠금 시 동적효과를 고려한 수압 상승으로 인해 응력이 각각 최대 27%, 86% 상승함을 알 수 있었다. 해석 결과 밸브 잠금 상태에서 소나돔 운용 시 일부 응력 상승은 발생할 수 있으나 Soderberg 안정도 판별법을 통해 검토한 결과 충분히 안전한 영역에 있음을 알 수 있었다. 하지만 죄굴 관점에서 보았을 때 밸브 잠금 시 슬래밍 step 4 조건 파손이 발생될 수 있음을 예측할 수 있었다.
본 연구의 해석에서 고려한 유체력은 해상상태나 함 조건에 따라 달라질 수 있으며 밸브 개폐에 따른 응력변화는 유체력을 어떻게 정의하느냐에 따라 달라질 수 있으므로 본 연구의 해석 결과는 실험을 통해 검증이 이루어져야 할 것으로 사료된다. 해석 결과로부터 소나돔의 충, 배수 밸브 잠금 시 응력 상승을 초래하기 때문에 함 운용 시 밸브는 개방하여 운용하는 것이 소나돔 윈도우의 구조안전성 측면에서는 보다 안전한 조건임을 파악할 수 있었다.
References
-
M. H. Kang, “Impact analysis for sonar domes collided with logs”, Journal of the Korea Institute of Military Science and Technology, 14(4), p564-571, (2011), (in Korean).
[https://doi.org/10.9766/KIMST.2011.14.4.564]

- J. Lee, and P. A. Wilson, “Experimental study of the hydro-impact of slamming in a modern racing sailboat”, Journal of Sailboat Technology, 1, p1-28, (2010).
-
T. K. Lee, C. W. Rim, Y. N. Kim, J. K. Heo, and B. H. Kim, “A study on measurement of flare slamming of large container vessel(Ⅱ) - characteristic analysis of measured slamming pressure”, Journal of the Society of Naval Architects of Korea, 44(3), p279-284, (2007), (in Korean).
[https://doi.org/10.3744/SNAK.2007.44.3.279]

-
J. H. Hwang, J. K. Park, and W. C. Koo, “Numerical analysis of ship motions and wave loads including momentum slamming”, Journal of the Society of Naval Architects of Korea, 49(2), p109-115, (2012), (in Korean).
[https://doi.org/10.3744/SNAK.2012.49.2.109]

- J. Y. Ko, “A study on the large deflection behavior of ship plate with secondary buckling”, Journal of Korean Society of Marine Engineering, 23(4), p565-573, (1999), (in Korean).
- B. V, “German armed forces shipbuilding regulation”, Geman, BV 1040-1, (1985).
- IACS, "Standard wave data, IACS Recommendation No. 34, (2001).