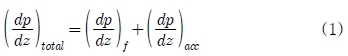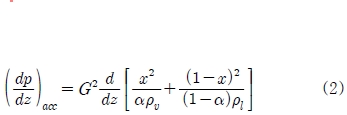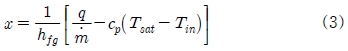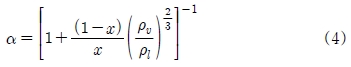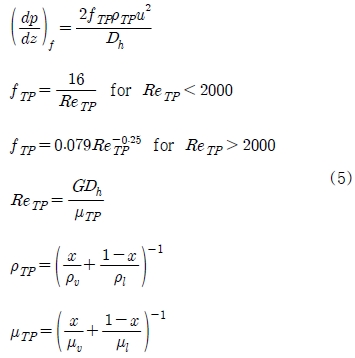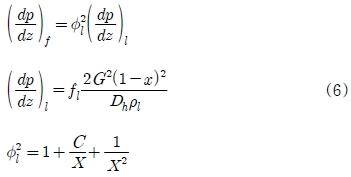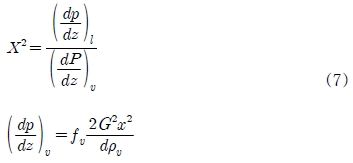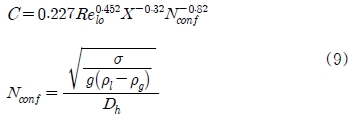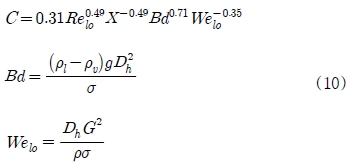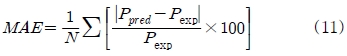[ Article ]

Journal of the Korean Society of Marine Engineering - Vol. 38, No. 7, pp.821-827

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date Sep 2014

Received 01 Jul 2014 Revised 29 Aug 2014 Accepted 02 Sep 2014

DOI: https://doi.org/10.5916/jkosme.2014.38.7.821

Prediction methods for two-phase flow frictional pressure drop of FC-72 in parallel micro-channels

ChoiYong-Seok¹ ; LimTae-Woo^† ; YouSam-Sang²

1Graduate School, Division of Marine Engineering, Korea Maritime and Ocean University 2Division of Mechanical and Energy Systems Engineering, Korea Maritime and Ocean University

병렬 마이크로 채널에서 FC-72의 2상 유동 마찰 압력 강하 예측

Correspondence to: ^† Division of Marine Engineering, Korea Maritime and Ocean University, Dongsam-dong, Yeongdo-gu, Busan, 606-791, Korea, E-mail: kyunlim@kmou.ac.kr, Tel: 051-410-4256

In this study, an experimental study was performed to predict the two-phase frictional pressure drop of FC-72 in parallel micro-channels. The parallel micro-channels consist of 15 channels with depth 0.2 mm, width 0.45 mm and length 60 mm. And tests were performed in the ranges of mass fluxes from 152.2 to 584.2 kg/m²s and heat fluxes from 7.5 to 28.3 kW/m². The experimental data was compared and analyzed with existing correlations to predict the pressure drop. The existing methods to predict the pressure drop used the homogeneous model and the separated model. In this study, the new correlation was proposed by modified existing correlation using the separated model, and the new correlation predicted consequently with the experimental data within MAE of 9.6%.

초록

본 연구에서는 FC-72를 작동유체로 사용하여 병렬 마이크로 채널에서의 2상 유동 마찰 압력 강하를 예측하기 위한 실험적 연구를 수행하였다. 병렬 마이크로 채널은 깊이 0.2 mm, 폭 0.45 mm, 길이 60 mm의 15개의 마이크로 채널로 구성되었으며, 실험은 질량유속 152.2~584.2 kg/m²s, 열유속 7.5~28.3 kW/m² 범위에서 이루어졌다. 실험에서 얻어진 자료는 기존의 마찰 압력 강하를 예측하기 위한 상관식들과 비교·분석하였다. 기존의 상관식은 일반적으로 균질 모델과 분리류 모델을 사용한다. 본 연구에서는 분리류 모델을 사용한 기존의 상관식을 수정하여 새로운 상관식을 제안하였으며, 그 결과 Mean Absolute Error 9.6%내에서 실험 결과를 잘 예측하였다.

Keywords:

FC-72, Micro-channels, Frictional pressure drop, Homogeneous model, Separated model, 마이크로 채널, 마찰 압력 강하, 균질 모델, 분리류 모델

1. 서 론

전자 장비 산업의 발달로 시스템과 부품들은 고성능, 고효율화를 추구하고 있으며 시스템의 부피도 점차 소형화 되는 추세에 있다. 이로 인해 시스템 내부에서 발생하는 열을 효과적으로 제거할 수 있는 기술 개발이 요구되고 있는 실정이다. 마이크로 채널을 이용한 히트싱크는 1981년 Tuckerman and Pease[1]에 의해 제안되어 현재까지도 많은 연구가 진행 중에 있다. 마이크로 채널에서의 열유동 특성은 매크로 채널과는 다르게 나타나는 것으로 보고되고 있으며, 특히 마이크로 채널은 체적당 면적비가 매우 높아 열소산 능력이 뛰어난 것으로 나타났다[2][3]. 마이크로 채널을 이용한 냉각시스템 구축을 위해서는 채널 내부의 압력 강하를 예측하는 것이 필수적이다[4].

Mishima and Hibiki[5]는 직경 1-4 mm의 튜브에서 공기-물의 2상 유동에 관한 실험을 수행하였으며, 관직경이 작아질수록 표면장력이 유동에 미치는 영향이 증가한다고 보고하였다.

Hwang and Kim[6]은 직경 0.244-0.792 mm의 마이크로 튜브에서 R-134를 작동유체로 사용하여 실험하였다. 그 결과 Mishima and Hibiki와 마찬가지로 표면장력이 압력 강하에 주요한 영향을 미치는 인자로 보았으며, 또한 레이놀즈 수 역시 마이크로 채널에서의 유동을 지배하는 인자로 파악하여 새로운 상관식을 제안하였다.

FC-72는 불활성 불소화합물로서 배관 내 녹이 슬지 않으며, 열적·화학적으로 안정적일뿐 아니라 비인화성 및 무독성 유체로서 유전율이 낮은 특징을 가지고 있다. 따라서 본 연구에서는 전기·전자 장비의 냉각 시스템의 냉매로서 활용성이 높을 것으로 예상되는 FC-72를 냉매로 선정하여 실험을 수행하였다.

본 연구에서는 15개의 병렬 마이크로 채널에서 유동 비등 시 압력 강하에 관한 실험을 수행하였으며, 실험을 통해서 얻어진 자료를 기존의 상관식들과 비교·분석하였으며, 이를 토대로 기존의 상관식을 수정하여 2상 유동시 압력 강하를 보다 정확하게 예측할 수 있는 새로운 상관식을 제안하였다.

2. 실험장치 및 방법

2.1 실험장치

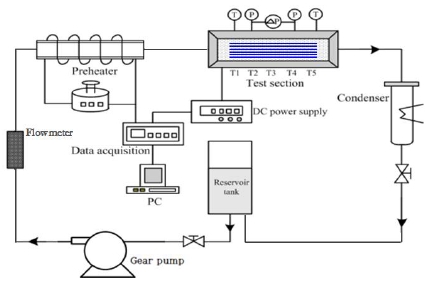
실험장치는 저장탱크, 기어펌프, 예열기 그리고 시험부로 구성되어 있으며 실험장치의 개략도를 Figure 1에 나타내었다. 작동유체는 FC-72를 사용하였으며, 작동유체는 저장탱크에서 기어펌프를 통해 유량계를 거쳐 예열기로 공급되어 일정한 온도까지 예열된 후 시험부로 유입된다. 시험부에서 재가열된 액체-증기 혼합물은 응축기에서 응축된 후 저장탱크로 모여 다시 사이클을 순환하는 폐회로 시스템으로 구성되었다.

Figure 1:

Schematic of experimental setup

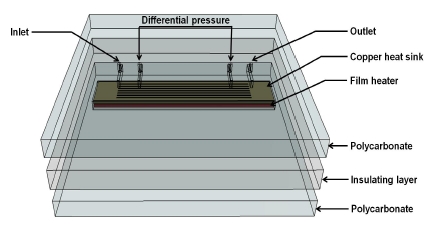
Figure 2는 시험부를 나타내며, 마이크로 채널의 깊이와 폭은 각각 0.2 mm, 0.45 mm이며, 개수는 15개로 구성되었다. 채널의 총길이는 60 mm이며, 압력 측정구간은 40 mm이다. 마이크로 채널이 있는 동판의 하부에는 필름히터가 부착되어 직류 전원 공급 장치를 통해 일정한 열량을 공급하게 된다. 직류 전원 공급 장치는 0~50V와 0~3A의 전압과 전류 범위 내에서 조절되며, 필름히터에 인가되는 전압과 전류를 측정하여 시험부에 전달되는 열량을 계산하게 된다. 동판과 필름히터 사이에 T-type 열전대 4개를 부착하여 온도를 측정하며, 열손실을 최대한 방지하기 위해 필름히터 하부에는 단열재를 설치하였다. 또한 동판의 상부에는 채널에서의 유동을 직접 관찰할 수 있도록 폴리카보네이트로 제작한 투명한 커버를 부착하였다. 폴리카보네이트 커버 내부에는 각 채널로 균일한 유동 분배를 위한 매니폴더가 존재한다.

Figure 2:

Test section

2.2 실험방법

실험을 시작하기 전에 약 1시간 동안 시스템내의 작동유체를 순환시킴으로써 예열기와 시험부의 필름히터를 통해 작동유체를 가열하여 증발시킴으로 가스제거(degassing) 작업을 수행하였다.

작동유체는 유량계에 의해 측정되며, 본 연구에서 작동유체의 유량은 7.7~29.4 ml/min 이며, 이는 질량유속 152.2~584.2 kg/m²s에 해당한다. 시험부의 열유속은 7.5~28.3 kW/m²이며, 이때 주어진 유량과 열유속에서의 출구건도 범위는 0~0.89이다.

작동유체의 입·출구 온도는 T-type 열전대를 사용하여 측정하였으며, 압력강하는 차압계를 사용하여 측정하였다. 실험에서 측정된 값들은 데이터 수집 장치(Data Acquisition Equipment; YOKOGAWA, GP-10)를 이용하여 수집 분석하였다. 측정된 값들의 불확실성은 유량과 압력강하의 경우 각각 풀 스케일에서 ±3%, ±0.25%이다. 또한, 온도 측정의 불확실성은 ±0.3℃이며, 열유속은 필름히터에 인가된 전압과 전류로 계산하였으며, 이때의 불확실성은 2~4%의 범위에 있다 [3]. 작동유체인 FC-72의 물성치는 제조사인 3M사에서 제공하는 자료를 이용하였다.

3. 결과 및 고찰

3.1 압력 강하

수평관내의 2상 유동에서 총 압력 강하는 식 (1)에 의해 구해진다.

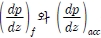는 각각 마찰 압력 강하와 2상 유동 시 가속에 의한 압력 강하를 나타낸다. 가속에 의한 압력강하는 식 (2)를 사용하여 계산하였다[7].

여기서 하첨자 ν와 l은 각각 기상과 액상을 의미한다. G는 질량유속, x는 건도를 나타내며, 건도는 에너지 평형에 의해 식 (3)과 같이 계산된다. 리고 α는 기공률을 나타내며, 기공률은 Zivi[8] 상관식을 사용하여 식 (4)과 같이 계산하였다.

여기서 h_fg는 증발잠열을 나타내며, q는 히트싱크를 통해 유체에 전달된 열량을 나타낸다.

실험에서 얻어진 총 압력강하에서 상기 식들을 이용하여 2상 유동 마찰 압력 강하를 계산하였다. 일반적으로 가속에 의한 압력 강하는 마찰 압력 강하에 비하여 작은 값을 가지며, 채널 내의 총 압력 강하를 정확하게 예측하기 위하여 마찰 압력 강하를 예측하는 것이 필수적이다.

3.2 2상 유동 압력 강하 모델

3.2.1 균질 모델(Homogeneous model)

균질 모델은 두 상이 잘 혼합되어 같은 속도로 움직인다고 가정한다. 즉 2상 유동을 두 상의 평균 물성치를 가지는 단상 유체의 유동으로 간주한다. 균질 모델을 이용한 마찰 압력 강하는 식 (5)로 나타낼 수 있다.

여기서 하첨자 TP는 2상 유동을 뜻하며, D_h는 수력직경을 나타낸다. 본 연구에서 사용된 채널의 수력직경은 0.277 mm이다.

3.2.2 분리류 모델(Separated flow model)

분리류 모델은 Lockhart and Martinelli[9]에 의해 제안되어 현재까지도 흔히 사용되고 있으며, 균질 모델과 달리 액상과 기상을 분리해서 각각 계산하게 된다. 분리류 모델의 상관식은 마찰 압력 강하를 이상 마찰 승수(Φ_l)에 관한 식으로 나타내며, 그 형태는 주로 식 (6)와 같다.

Lockhart and Martinelli는 변수 C를 액상과 기상의 유동형태에 따른 상수로 정의하였다. 액상과 기상 모두 난류일 때의 C값을 20, 모두 층류일 때는 5, 층류의 액상과 난류의 기상에서는 12 그리고 난류의 액상과 층류의 기상에서는 10으로 제안하였다. Martinneli 변수 X는 식 (7)과 같이 주어진다.

Mishima and Hibiki는 관직경의 영향을 고려하여 변수 C를 식 (8)과 같이 제안하였다.

Hwang and Kim은 직경 0.244-0.792 mm의 마이크로 튜브에서 R-134를 작동유체로 사용하여 실험하였다. 그 결과 Mishima and Hibiki와 마찬가지로 표면장력이 마이크로 채널의 유동에서 주요한 영향을 미치는 인자로 보았으며, 또한 Re 수 역시 주요한 인자로 판단하여 식 (8)과 같은 상관식을 제안하였다

하첨자 lo는 전체 유량이 액체 유량이라고 가정한다는 것을 의미한다.

Li and Wu[10][11] 역시 본드 수(Bd)와 레이놀즈 수가 마이크로 채널에서의 비등 유동을 지배하는 주요 무차원수로 보고하였다. 본드 수는 표면장력에 대한 체적력의 비로 정의되며, 채널의 수력직경이 줄어들면 채널내의 기포는 압착되고, 표면장력이 점차 유동을 지배하는 주요 원인이 된다고 밝혔다. 본 연구에서는 레이놀즈 수, 본드 수, 웨버 수(We)를 이용하여 Hwang and Kim 상관식을 다음과 같이 수정하였다.

3.3 결과분석

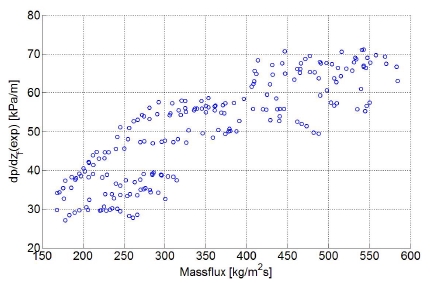
Figure 3은 질량유속변화에 따른 마찰 압력 강하를 나타내었다. 질량유속이 증가함에 따라 마찰 압력 강하도 증가하는 것을 알 수 있다.

Figure 3:

Pressure drop with respect to mass flux

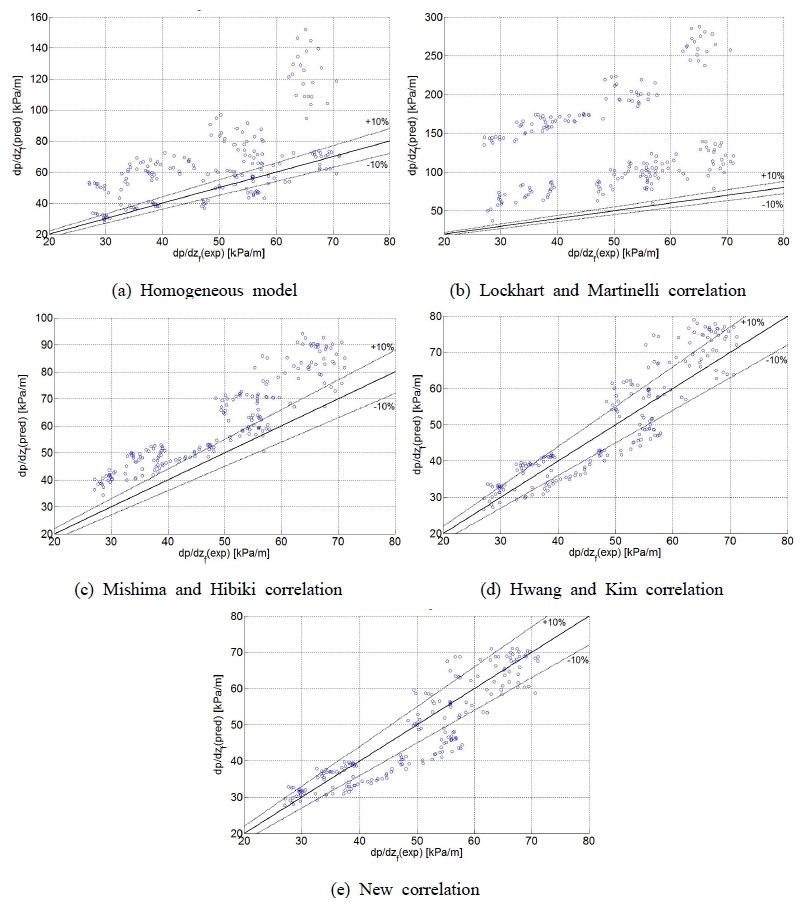
Figure 4는 측정된 마찰 압력 강하에 대한 여러 상관식들의 마찰 압력 강하 예측치를 비교해서 나타내었다. 실험 결과와 상관식들의 비교는 MAE(mean absolute error)를 사용하여 판단하였으며, MAE는 다음과 같이 정의된다.

Figure 4:

Comparison of experimental data and predicted frictional pressure drop

매크로 채널에서 주로 적용되는 균질 모델과 Lockhart and Martinelli 상관식의 경우 실험 결과에 비해 마찰 압력 강하를 높게 예측하였으며, 특히 Lockhart and Martinelli 상관식은 매크로 채널에서 개발된 상관식으로 유동형태에 따라 변수 C의 값을 상수로 정의하였는데, 마이크로 채널 유동에 경우 대부분의 액상 유동은 층류에 해당되며 기상 유동은 높은 질량유속과 높은 건도에서는 난류에 해당된다. 그에 따라 예측값에서 많은 오차를 보이는 것으로 판단된다.

Table 1은 현 실험 결과와 균질모델을 포함한 상관식들 사이의 MAE를 나타내고 있다. 미니 채널에서 개발된 Mishima and Hibiki 상관식은 MAE 25.5% 내에서 본 실험 결과를 비교적 정확하게 예측하고 있으나, 전체적으로 다소 높게 예측하였다. Hwang and Kim 상관식은 11.5%의 MAE내에서 기존의 상관식들 중에서 본 실험 결과를 가장 잘 예측하는 것으로 나타났다. 하지만 질량유속이 증가할수록 오차가 증가하는 것으로 나타났다.

Table 1:

Mean absolute error

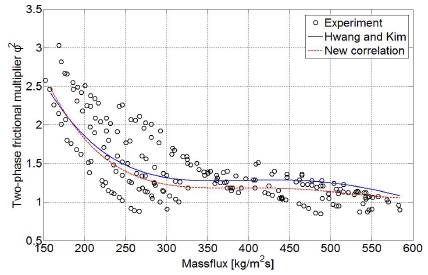
Figure 5는 질량유속 변화에 따른 실험값과 상관식에 의한 이상마찰승수를 비교한 것으로 높은 질량유속에서 Hwang and Kim 상관식의 이상마찰승수는 실험값에 비해 큰 값을 가지며, 이에 따라 높은 질량유속에서 마찰 압력 강하를 높게 예측한 것으로 판단된다. 이에 반해, 본 연구에서 제안한 상관식은 높은 질량유속에서 실험값과 근사하게 이상마찰승수를 예측하고 있으며, 높은 마찰 압력 강하에서도 비교적 정확하게 예측하였다. 그 결과 MAE 9.6%내에서 실험 결과를 잘 예측하는 것으로 나타났다.

Figure 5:

Comparison of experimental and predicted two-phase frictional multiplier

5. 결 론

본 연구에서는 병렬 마이크로 채널에서 FC-72의 2상 유동 마찰 압력 강하에 관한 실험을 수행하였으며, 다음과 같은 결론을 얻었다.

1. 균질 모델과 매크로 채널에서 개발된 Lockhart and Martinelli 상관식을 마이크로 채널에 적용 시 많은 오차가 발생하였으며, 마찰 압력 강하를 정확하게 예측할 수 없었다.

2. Hwang and Kim의 상관식은 MAE 11.5%로 본 연구의 실험 결과 내에서 비교적 정확하게 예측하였으나, 질량유속이 증가할수록 오차는 증가하였다.

3. 본 연구에서는 레이놀즈 수, 본드 수, 웨버 수를 이용하여 새로운 상관식을 제안하였으며, 그 결과 MAE 9.6%내에서 실험 결과를 잘 예측하였다. 또한 높은 질량유속에서 기존의 Hwang and Kim 상관식에 비해 정확하게 예측하였다.

Acknowledgments

본 과제(결과물)는 해양수산부의 지원으로 수행한 해양에너지 전문인력 양성사업의 연구 결과입니다.

References

B. D. Tuckerman, and R. F. W. Pease, “High-performance heat sinking for VLSI”, IEEE Electronic Device Letters, 2(5), p126-129, (1981). [https://doi.org/10.1109/EDL.1981.25367]
S. Kandlikar, S. Garimella, D. Li, S. Colin, and M. King, Heat Transfer and Fluid Flow in Minichannels and Microchannels, ELSEVEIR, (2006).
T. W. Lim, S. S. You, H. S. Choi, and D. H. Kim, “Boiling heat transfer characteristics of deionized water in micro channel”, Journal of the Korea Society of Marine Engineering, 35(6), p750-756, (2011), (in Korean).
Y. S. Choi, T. W. Lim, S. S. You, and J. Y. Noh, “Prediction methods for two-phase flow pressure drop in micro-channels”, Proceedings of the 38^th KOSME Springs Conference, p266, (2014), (in Korean).
K. Mishima, and T. Hibiki, “Some characteristics of air-water two-phase flow in small diameter vertical tubes”, International Journal of Multiphase Flow, 22(4), p703-712, (1996). [https://doi.org/10.1016/0301-9322(96)00010-9]
Y. W. Hwang, and M. S. Kim, “The pressure drop in microtubes and the correlation development”, International Journal of Heat and Mass Transfer, 49, p1804-1812, (2006).
J. G. Collier, and J. R. Thome, Convective Boiling and Condensation, 3rd ed, Oxford University Press, (1994).
S. M. Zivi, “Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production”, Transactions of American Society of Mechanical Engineers (Journal of Heat Transfer), 86, p247-251, (1964). [https://doi.org/10.1115/1.3687113]
R. W. Lockhart, and R. C. Martinelli, “Proposed correlation of data for isothermal two-component flow in pipes”, Chemical Engineering Progress, 45, p39-48, (1949).
W. Li, and Z. Wu, “A general criterion for evaporative heat transfer in micro/mini-channels”, International Journal of Heat and Mass Transfer, 53, p1967-1976, (2010). [https://doi.org/10.1016/j.ijheatmasstransfer.2009.12.059]
W. Li, and Z. Wu, “A general correlation for adiabatic two-phase pressure drop in micro/mini-channels”, International Journal of Heat and Mass Transfer, 53, p2732-2739, (2010). [https://doi.org/10.1016/j.ijheatmasstransfer.2010.02.029]